控制系统/反馈回路

维基教科书的

控制系统

与控制工程

所有版本

反馈

反馈回路是设计控制系统时一种常见且强大的工具。反馈回路考虑了系统输出，使系统能够调整其性能以满足所需的输出响应。

在谈论控制系统时，重要的是要记住，工程师通常会得到现有的系统，例如执行器、传感器、电机和其他具有设定参数的设备，并被要求调整这些系统的性能。在许多情况下，可能无法打开系统（“对象”）并从内部进行调整：需要对系统外部进行修改，以迫使系统响应按预期方式运作。这是通过在系统中添加控制器、补偿器和反馈结构来实现的。

基本反馈结构

维基百科在反馈中有相关信息。

这是一个基本的反馈结构。在这里，我们使用系统的输出值来帮助我们准备下一个输出值。这样，我们就可以创建能够纠正错误的系统。在这里，我们看到一个值为一的反馈回路。我们称之为单位反馈。

以下是一些将在以下部分中使用的相关词汇列表

对象: 术语“对象”是从化学工程中借用的，指的是主要的系统过程。对象是预先存在的系统，如果没有控制器的帮助，它将无法满足给定的规格。对象通常是“现有的”，并且不可更改。在上图中，对象用 P 表示。
控制器: 控制器或“补偿器”是添加到对象中的一个附加系统，以控制对象的运行。系统可以有多个补偿器，它们可以出现在系统的任何地方：在取样节点之前，在求和器之后，在对象之前或之后，以及在反馈回路中。在上图中，我们的补偿器用 C 表示。

一些文本或其他学科的文本可能将“求和器”称为加法器。

求和器: 求和器是系统图上的一个符号（在上图中用括号表示），它在概念上将两个或多个输入信号相加，并产生一个单一的和输出信号。
取样节点: 取样节点仅仅是线路上分支的代名词。
前向通路: 反馈回路中的前向通路是求和器之后，穿过对象并走向系统输出的通路。
反向通路: 反向通路是取样节点之后，循环回系统开始的通路。这也被称为“反馈通路”。
单位反馈: 当反馈通路的乘法值为 1 时。

负反馈与正反馈

事实证明，负反馈几乎总是最有用的反馈类型。当我们将输出值从输入值（我们期望的值）中减去时，我们得到一个称为误差信号的值。误差信号显示了我们的输出与我们期望的输入相差多远。

正反馈具有信号倾向于自我增强并变大的特性。在正反馈系统中，来自系统的噪声被加回到输入，这反过来又会产生更多噪声。作为一个正反馈系统的例子，考虑一个带有扬声器和麦克风的音频放大系统。将麦克风放置在扬声器附近会创建一个正反馈回路，结果是声音变得越来越响亮。由于大多数电气系统中的噪声都是高频的，因此系统的声输出会变得尖锐。

示例：状态空间方程

在上一章中，我们向您展示了这张图片

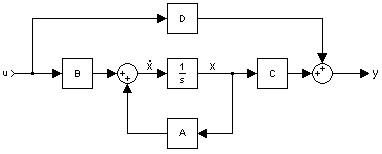
现在，我们将推导出 I/O 关系到状态空间方程。如果我们检查最里面的反馈回路，我们可以看到前向通路有一个积分器系统， ${\frac {1}{s}}$ ，反馈回路具有矩阵值 A。如果我们只取这个回路的传递函数，我们会得到

T_{inner}(s)={\frac {\frac {1}{s}}{1-{\frac {1}{s}}A}}={\frac {1}{s-A}}

用因子 B 左乘，用 C 右乘，我们得到整个下半部分回路的传递函数

T_{lower}(s)=B\left({\frac {1}{s-A}}\right)C

我们可以看到上通路（D）和下通路 T_lower 相加在一起产生最终结果

T_{total}(s)=B\left({\frac {1}{s-A}}\right)C+D

现在，对于另一种方法，我们可以假设x' 是最里面的反馈回路的值，位于积分器之前。这是有道理的，因为x' 的积分应该是x（从图中我们可以看到它确实是这样的。用u 作为输入，解出x'，我们得到

x'=Ax+Bu

这是因为来自反馈分支的值等于值 **x** 乘以反馈回路矩阵 A，而来自求和器左侧的值等于输入 **u** 乘以矩阵 B。

如果我们用 **x** 和 **u** 来表示，我们可以看到系统输出是 **u** 乘以前馈值 D 和 **x** 的值乘以值 C 的总和。

y=Cx+Du

最后两个方程正是我们系统的状态空间方程。

反馈回路传递函数

我们可以通过一系列方程来求解系统的输出。

E(s)=X(s)-Y(s)

Y(s)=G(s)E(s)

当我们解出 Y(s) 时，得到

[反馈传递函数]

Y(s)=X(s){\frac {Gp(s)}{1+Gp(s)}}

鼓励读者自己使用上述方程推导出结果。

函数 E(s) 被称为 **误差信号**。误差信号是系统输出 (Y(s)) 和系统输入 (X(s)) 之间的差。请注意，误差信号现在是系统 G(s) 的直接输入。X(s) 现在被称为 **参考输入**。负反馈回路的目的是通过识别 X(s) 和 Y(s) 之间的较大差异并对其进行校正，使系统输出等于系统输入。

示例：电梯

这是一个关于参考输入和反馈系统的简单示例。

某栋楼里有一部电梯，有 5 层楼。按下按钮“1”会把你送到一楼，按下按钮“5”会把你送到五楼，等等。为了简单起见，一次只能按一个按钮。

按下特定的按钮是系统的参考输入。按下“1”会给系统一个参考输入 1，按下“2”会给系统一个参考输入 2，等等。然后，电梯系统试图使输出（电梯的物理楼层位置）与参考输入（在电梯中按下的按钮）匹配。误差信号 e(t) 表示参考输入 x(t) 和时间 t 时电梯的物理位置 y(t) 之间的差异。

假设电梯在一楼，并且在时间 t₀ 时按下了按钮“5”。然后参考输入成为一个阶跃函数。

x(t)=5u(t-t_{0})

我们在“楼层”单位中测量。在时间 t₀ 时，误差信号为

e(t_{0})=x(t_{0})-y(t_{0})=5-1=4

这意味着电梯需要向上行驶 4 层。在时间 t₁ 时，当电梯在二楼时，误差信号为

e(t_{1})=x(t_{1})-y(t_{1})=5-2=3

这意味着电梯还有 3 层要走。最后，在时间 t₄ 时，当电梯到达顶层时，误差信号为

e(t_{4})=x(t_{4})-y(t_{4})=5-5=0

当误差信号为零时，电梯停止移动。本质上，我们可以定义三种情况。

e(t) 为正数：在这种情况下，电梯向上移动一层，然后再次检查。
e(t) 为零：电梯停止。
e(t) 为负数：电梯向下移动一层，然后再次检查。

状态空间反馈回路

在状态空间表示中，工厂通常由状态空间方程定义。

x'(t)=Ax(t)+Bu(t)

y(t)=Cx(t)+Du(t)

该系统被认为是预先存在的，矩阵 A、B、C 和 D 被认为是系统内部的（因此不可更改）。此外，在典型的系统中，状态变量要么是虚构的（表示为虚拟变量），要么是不可测量的。出于这些原因，我们需要向系统添加外部组件，例如增益元件或反馈元件，以提高性能。

考虑在系统输入端添加增益矩阵 K，以及一个负反馈元件 F，该元件乘以系统输出 y 并添加到系统的输入信号中。有两种情况

反馈元件 F 在乘以增益矩阵 K 之前从输入中减去。
反馈元件 F 在乘以增益矩阵 K 之后从输入中减去。

在情况 1 中，反馈元件 F 在将增益乘以输入之前添加到输入中。如果 v 是整个系统的输入，那么我们可以定义 u 为

u(t)=Fv(t)-FKy(t)

在情况 2 中，反馈元件 F 在将增益乘以输入之后从输入中减去。如果 v 是整个系统的输入，那么我们可以定义 u 为

u(t)=Kv(t)-Fy(t)

开环与闭环

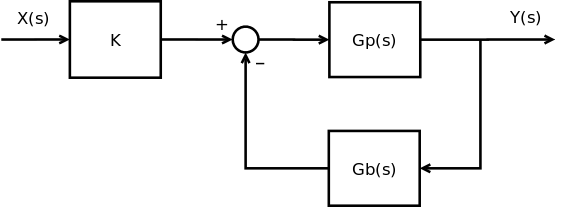
假设我们有上面所示的广义系统。顶部部分，Gp(s) 表示所有正向路径上的系统和控制器。底部部分，Gb(s) 表示系统中所有反馈处理元件。系统开头的字母“K”称为**增益**。我们将在后面的章节中更多地讨论增益。我们可以定义**闭环传递函数**如下

[闭环传递函数]

H_{cl}(s)={\frac {KGp(s)}{1+Gp(s)Gb(s)}}

如果我们“打开”循环，并断开反馈节点，我们可以定义**开环传递函数**，如下所示

[开环传递函数]

H_{ol}(s)=KGp(s)

我们可以根据这个开环传递函数重新定义闭环传递函数

H_{cl}(s)={\frac {H_{ol}(s)}{1+Gp(s)Gb(s)}}

这些结果很重要，它们将在本书的其余部分中使用，无需进一步解释或推导。

控制器的放置

我们可以将附加控制器放置在许多不同的位置。


在系统前面，在反馈回路之前。在反馈回路内，在正向路径上，在系统之前。在正向路径上，在系统之后。在反馈回路内，在反向路径上。在反馈回路之后。