控制系统/根轨迹

问题

考虑像收音机这样的系统。收音机有一个“音量”旋钮，用于控制系统的增益。高音量意味着更多功率传递到扬声器，低音量意味着更少功率传递到扬声器。当音量值增加时，收音机传递函数的极点会发生变化，它们可能变得不稳定。我们想要找出收音机是否会变得不稳定，如果是，我们想要找出哪些音量值会导致它变得不稳定。我们目前的方法需要我们为每个新的音量值（增益，“K”）代入，并求解开环传递函数的根。这个过程可能很长。幸运的是，有一种名为根轨迹的方法，它允许我们为所有增益值绘制系统所有极点的位置图。

根轨迹

当我们改变增益时，我们注意到系统的极点和零点实际上在S 平面中移动。当我们需要为每个新的增益值重复求解高阶方程时，这一事实会让生活变得非常困难。解决这个问题的办法是一种称为根轨迹图的技术。根轨迹允许您通过遵循几个简单的规则来绘制所有增益值的极点和零点的位置图。正如我们所知，风扇开关也可以控制风扇的速度。

假设我们有一个特定系统的闭环传递函数

${\frac {N(s)}{D(s)}}={\frac {KG(s)}{1+KG(s)H(s)}}$

其中 N 是传递函数的分子多项式，D 是传递函数的分母多项式。现在，我们知道要找到方程的极点，我们必须将分母设为 0，并求解特征方程。换句话说，特定方程的极点位置必须满足以下关系

$D(s)=1+KG(s)H(s)=0$

从同一个方程中，我们可以这样操作方程

$1+KG(s)H(s)=0$

$KG(s)H(s)=-1$

最后，通过转换为极坐标

$\angle KG(s)H(s)=180^{\circ }$

现在我们有两个方程控制着系统所有增益值的极点位置

[幅值方程]

$1+KG(s)H(s)=0$

[相位方程]

$\angle KG(s)H(s)=180^{\circ }$

数字系统

相同的基本方法可用于考虑 Z 域中的数字系统

${\frac {N(z)}{D(z)}}={\frac {KG(z)}{1+K{\overline {GH}}(z)}}$

其中 N 是关于 z 的分子多项式，D 是关于 z 的分母多项式，${\overline {GH}}(z)$ 是系统的开环传递函数，在 Z 域中。

根据特征方程的定义，分母 D(z) 等于

$D(z)=1+K{\overline {GH}}(z)=0$

我们可以如下操作

$1+K{\overline {GH}}(z)=0$

$K{\overline {GH}}(z)=-1$

现在我们可以将其转换为极坐标，并取多项式的角度

$\angle K{\overline {GH}}(z)=180^{\circ }$

现在我们只剩下两个重要的方程

[幅值方程]

$1+K{\overline {GH}}(z)=0$

[相位方程]

$\angle K{\overline {GH}}(z)=180^{\circ }$

如果您比较这两个方程，Z 域方程与 S 域方程几乎完全相同，作用方式也完全相同。在本章的剩余部分，我们将只考虑 S 域方程，并且理解数字系统以几乎相同的方式运行。

根轨迹法

注意
在本节中，S 平面和 Z 平面的规则相同，因此我们将不提及它们之间的差异。

在变换域（参见右侧注释）中，当增益较小时，极点从开环传递函数的极点开始。当增益变为无穷大时，极点移动到与系统的零点重叠。这意味着在根轨迹图上，所有极点都朝零点移动。只有一个极点可以朝一个零点移动，这意味着极点的数量必须与零点的数量相同。

如果传递函数中的零点少于极点，则存在一定数量的隐式零点位于无穷远处，极点将趋近于这些零点。

首先，我们需要将幅值方程转换为稍微方便一点的形式

$KG(s)H(s)+1=0\to G(s)H(s)={\frac {-1}{K}}$

注意
我们通常用大写字母表示频域中的函数，但a(s)和b(s)并不重要，因此用小写字母表示。

现在，我们可以假设 G(s)H(s) 是某种形式的分数，其分子和分母都是多项式。我们可以使用任意函数 a(s) 和 b(s) 来表示这个方程，如下所示

${\frac {a(s)}{b(s)}}={\frac {-1}{K}}$

我们将在后面的步骤中用到这些函数 a(s) 和 b(s)。

我们可以首先在图上用“X”标记 b(s) 的根来开始绘制根轨迹。接下来，我们在图上标记 a(s) 的根，并用“O”标记它们。

接下来，我们检查实轴。从图的右侧开始，向左移动，我们在实轴上每经过一个实轴上奇数个极点或零点的左侧，就绘制一条根轨迹线。这乍一看可能很棘手，但随着练习会变得更容易。

现在，根轨迹线从每个极点开始。因此，在实轴上，如果两个极点似乎通过根轨迹线相连，则这两个极点实际上会相互靠近，然后“分离”，并离开轴线。极点离开轴线的位置称为分离点。从这里，根轨迹线朝最近的零点移动。

重要的是要注意，s 平面关于实轴对称，所以在 S 平面的上半部分绘制的内容，必须在 S 平面的下半部分以镜像方式绘制。

一旦极点从实轴分离，它们可以朝无穷远移动（以遇到隐式零点），或者它们可以移动以遇到显式零点，或者它们可以重新加入实轴以遇到位于实轴上的零点。如果极点朝无穷远移动，它总是遵循一条渐近线。渐近线的数量等于无穷远处的隐式零点的数量。

根轨迹法则

以下是绘制根轨迹图的完整规则集。我们将使用 p 和 z 分别表示开环传递函数的极点和零点的数量。我们将使用 P_i 和 Z_i 分别表示第 i 个极点和第 i 个零点的位置。同样，我们将使用 ψ_i 和 ρ_i 分别表示从给定点到第 i 个极点和零点的角度。所有角度都以弧度表示（π 表示 π 弧度）。

有 11 条规则，如果正确遵循，将使您能够创建正确的根轨迹图。

规则 1

对于 b(s) 的每个根，都有一个根轨迹分支。

规则 2

b(s) 的根是开环传递函数的极点。用 X 在图上标记 b(s) 的根。

规则 3

a(s) 的根是开环传递函数的零点。用 O 在图上标记 a(s) 的根。O 的数量应该小于或等于 X 的数量。在无穷远处有 p - z 个零点。这些位于无穷远处的零点被称为“隐式零点”。根轨迹的所有分支将从一个极点移动到一个零点（因此，一些分支可能会朝无穷远移动）。

规则 4

如果实轴上的一点位于奇数个极点和零点的左侧，则该点是根轨迹的一部分。

规则 5

可以通过幅值方程绝对值的倒数来确定根轨迹上任何点的增益。

$\left|{\frac {b(s)}{a(s)}}\right|=|K|$

规则 6

根轨迹图关于实轴对称。所有复根都是共轭的。

规则 7

在实轴上相遇的两个根将在某些分离点离开轴线。如果我们将 s → σ（没有虚部），我们可以使用以下方程

$K=-{\frac {b(\sigma )}{a(\sigma )}}$

然后求导以找到局部最大值

${\frac {dK}{d\sigma }}={\frac {d}{d\sigma }}{\frac {b(\sigma )}{a(\sigma )}}$

规则 8

根轨迹的分离线以 ${\frac {\pi }{\alpha }}$ 的角度分开，其中 α 是在分离点相交的极点的数量。

规则 9

根轨迹的分离线遵循渐近线，这些渐近线与实轴的交点角度为 φ_ω，其值由下式给出：

$\phi _{\omega }={\frac {\pi +2N\pi }{p-z}},\quad N=0,1,...p-z-1$

这些渐近线的起点 OA 由极点位置之和减去零点位置之和，再除以极点和零点数量之差得出。

$OA={\frac {\sum _{p}P_{i}-\sum _{z}Z_{i}}{p-z}}$

OA 点应该位于实轴上。

规则 10

根轨迹的分支在 **角度方程** 值为 π（即 180^o）的点处与虚轴相交。

规则 11

根轨迹分支与复共轭极点或零点的交角由在极点或零点附近无穷小位置分析 **角度方程** 得出。离开角 φ_d 由以下方程给出：

$\sum _{p}\psi _{i}+\sum _{z}\rho _{i}+\phi _{d}=\pi$

到达角 φ_a 由下式给出：

$\sum _{z}\rho _{i}+\sum _{p}\psi _{i}+\phi _{a}=\pi$

我们将在本章的剩余部分解释这些规则。

根轨迹方程

以下是两个主要方程

[根轨迹方程]

S 域方程	Z 域方程
$1+KG(s)H(s)=0$	$1+K{\overline {GH}}(z)=0$
$\angle KG(s)H(s)=180^{o}$	$\angle K{\overline {GH}}(z)=180^{o}$

注意，所有极点和零点的角度之和必须等于 180。

渐近线数量

如果系统显式零点的数量用 Z（大写 z）表示，系统的极点数量用 P 表示，那么渐近线的数量（N_a）由下式给出：

[渐近线数量]

$N_{a}=P-Z$

渐近线的角度由下式给出：

[渐近线角度]

$\phi _{k}=(2k+1){\frac {\pi }{P-Z}}$

当$k=[0,1,...N_{a}-1]$时。

渐近线交点

渐近线与实轴相交于点

[渐近线原点]

$\sigma _{0}={\frac {\sum _{P}-\sum _{Z}}{P-Z}}$

其中$\sum _{P}$是所有极点位置的总和，$\sum _{Z}$是所有显式零点位置的总和。

分离点

分离点位于以下方程的根处

[分离点位置]

${\frac {dG(s)H(s)}{ds}}=0$ 或 ${\frac {d{\overline {GH}}(z)}{dz}}=0$

求解 z 后，实根会给出分离点/重入点。复根对应于没有分离点/重入点。

分离点方程可能难以求解，因此很多时候实际位置是近似的。

根轨迹和稳定性

根轨迹过程应该生成一个图，显示系统的所有增益 K 值下的极点位置。当 D 的任何或所有根都位于不稳定区域时，系统是不稳定的。当任何根都位于临界稳定区域时，系统是临界稳定的（振荡的）。当 D 的所有根都位于稳定区域时，系统是稳定的。

需要注意的是，对于增益 K₁ 稳定的系统，对于不同的增益 K₂ 可能变得不稳定。一些系统可能具有在稳定和不稳定之间多次交叉的极点，从而导致多个增益值使系统不稳定。

以下是快速复习

区域	S 域		Z 域
稳定区域	左半 S 平面	$\sigma <0$	单位圆内	$|z|<1$
临界稳定区域	纵轴	$\sigma =0$	单位圆	$|z|=1$
不稳定区域	右半 S 平面	$\sigma >0$	单位圆外	$|z|>1$

示例

示例 1：一阶系统

求开环系统的根轨迹

$T(s)={\frac {1}{1+2s}}$

如果我们观察特征方程，我们可以快速求解系统的单个极点

$D(s)=1+2s=0$

$s=-{\frac {1}{2}}$

我们在根轨迹图上绘制该点，并且该单个点左侧实轴上的所有点都在根轨迹上（根据上述规则）。因此，我们系统的根轨迹看起来像这样

从这张图中，我们可以看出，对于所有增益值，该系统都是稳定的。

示例 2：三阶系统

我们得到一个具有三个实极点的系统，由传递函数表示

$T(s)={\frac {1}{(s+1)(s+2)(s+3)}}$

这个系统稳定吗？

为了回答这个问题，我们可以绘制根轨迹。首先，我们在图上绘制位于 -1、-2 和 -3 的极点。第一个和第二个极点之间的实轴以及第三个极点左侧的实轴都在根轨迹上。我们还知道，在某个点上会从实轴分离。渐近线的原点位于

$OA={\frac {-1+-2+-3}{3}}=-2$,

并且渐近线的角度由下式给出

$\phi ={\frac {180(2k+1)}{3}}\;\mathrm {for} \;k=0,1,2$

我们知道分离发生在第一个和第二个极点之间，因此我们将估计确切的分离点。绘制根轨迹后，我们得到以下图形。

我们可以看到，对于较低的增益值，系统是稳定的，但是对于较高的增益值，系统变得不稳定。

示例：共轭复零点

求以下系统传递函数的根轨迹图

$T(s)=K{\frac {s^{2}+4.5s+5.625}{s(s+1)(s+2)}}$

如果我们观察分母，我们有位于原点、-1 和 -2 的极点。根据 **规则 4**，我们知道第一个和第二个极点之间的实轴以及第三个极点之后的实轴都在根轨迹上。我们还知道，在第一个和第二个极点之间会有一个分离点，这样它们才能接近共轭复零点。如果我们对分子使用二次方程，我们可以发现零点位于

$s=(-2.25+j0.75),(-2.25-j0.75)$

如果我们绘制我们的图形，我们将得到以下结果

我们可以从该图中看出，对于所有 K 值，该系统都是稳定的。

示例：使用 MATLAB/Octave 绘制根轨迹

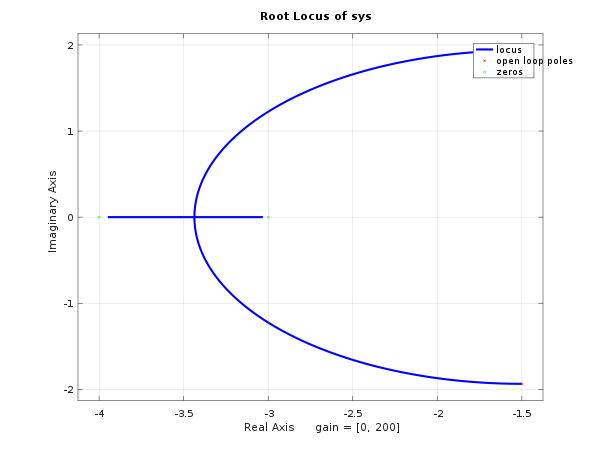
{{TextBox|1=使用 MATLAB、Octave 或其他数学仿真软件为以下系统生成根轨迹图

$T(s)=K{\frac {s^{2}+7s+12}{(s^{2}+3s+6)}}$

首先，我们必须将分母展开

$N(s)=S^{2}+7S+12$

$D(s)=S^{2}+3S+2$

现在，我们可以从分子和分母生成系数向量

 num = [0 1 7 12];
 den = [0 1 3 2];

接下来，我们可以将这些向量输入到 **rlocus** 命令中

 rlocus(num, den);

**注意**: 在 Octave 中，我们需要首先通过输入以下命令创建系统结构：

 sys = tf(num, den);
 rlocus(sys);

无论哪种方式，我们都会生成以下图表

← Jury 检验

控制系统

奈奎斯特稳定性判据 →