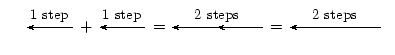FHSST 物理/向量/数学性质

向量的数学性质

向量是数学对象，我们将用它们来用数学语言描述物理。但是，首先我们需要了解向量的数学性质（例如它们如何加减）。

我们现在将使用表示位移的箭头来说明向量的性质。请记住，位移只是向量的一个例子。我们也可以选择使用力来说明向量的性质。

向量的加法

如果我们将位移向量定义为向前方向两步，而另一个定义为向前方向三步，那么将它们加在一起将意味着向前移动总共五步。从图形上看，这可以通过首先沿着第一个向量向前两步，然后沿着第二个向量向前三步来实现。

我们将第二个向量加在第一个向量的末端，因为这是第一个向量作用后我们现在的位置。从第一个向量的尾部（起点）到最后一个向量的头部（终点）的向量是所有向量的总和。这就是向量加法的头尾相连法。

向量相加的顺序无关紧要。在上面的例子中，如果你先向前走三步，然后再向前走两步，最终的结果仍然是向前走五步。

向量相加的最终答案称为合向量。

定义：若干个向量的合向量是指单个向量，其作用与所有向量共同作用产生的效果相同。

换句话说，可以用合向量来代替各个向量——总的效果是一样的。如果向量 ${\overrightarrow {a}}$ 和 ${\overrightarrow {b}}$ 的合向量为 ${\overrightarrow {R}}$，则可以用以下数学公式表示：${\begin{matrix}{\overrightarrow {R}}&=&{\overrightarrow {a}}+{\overrightarrow {b}}.\end{matrix}}$

让我们再考虑一些使用位移的向量加法的例子。箭头告诉你在哪个方向移动多远。指向右边的箭头对应于向前移动，而指向左边的箭头对应于向后移动。查看下面所有的例子并检查它们。

让我们测试第一个。它说向前一步，然后再向前一步，与一个长度是两倍的箭头相同——向前两步。

你可能会回到原点。在这种情况下，你所做的事情的最终结果是你什么地方都没有去过（你的起点和终点在同一个位置）。在这种情况下，你的合位移是一个长度为零单位的向量。我们使用符号 ${\overrightarrow {0}}$ 来表示这样的向量。

以同样的方式检查下面的例子。指向页面的箭头可以看作是向左移动，指向页面下方的箭头可以看作是向右移动。

尝试几个来让自己信服！

重要的是要认识到方向并不特殊——向前和向后或向左和向右的处理方式相同。任何一组平行方向也是如此。

在上面的例子中，各个位移彼此平行。但是，相同的头尾相连的向量加法技术可以应用于任何方向的向量。

现在你已经发现了向量的一个用途；描述合位移——经过一系列移动后你移动了多远，哪个方向。

虽然这里向量加法是通过位移来演示的，但所有向量都以完全相同的方式工作。因此，如果给定多个力作用于一个物体上，你可以使用相同的方法来确定作用在物体上的合力。我们将在后面详细介绍向量加法。

向量的减法

减去一个向量是什么意思？这很简单：如果我们有 5 个苹果，然后减去 3 个苹果，就只剩下 2 个苹果。现在让我们用步数来进行——如果我们向前走了 5 步，然后减去向前走了 3 步，就只剩下向前走了两步。

我们做了什么？你最初向前走了 5 步，然后向后走了 3 步。向后的位移将由一个指向左侧（向后）的箭头表示，长度为 3。添加这两个向量的最终结果是向前走了 2 步。

因此，从另一个向量中减去一个向量与添加一个方向相反的向量是一样的（即减去向前走 3 步与添加向后走 3 步相同）。

这表明在这个问题中，指向右边的箭头是正的，而指向左边的箭头是负的。更一般地说，方向相反的向量符号不同（即，如果我们将向上定义为正，那么向下作用的向量为负）。因此，改变向量的符号只是将它的方向反转。

用数学形式表示，从 ${\overrightarrow {b}}$ 中减去 ${\overrightarrow {a}}$ 会得到一个新的向量 ${\overrightarrow {c}}$

${\begin{matrix}{\overrightarrow {c}}&=&{\overrightarrow {b}}-{\overrightarrow {a}}\\&=&{\overrightarrow {b}}+(-{\overrightarrow {a}})\end{matrix}}$

这清楚地表明，从 ${\overrightarrow {b}}$ 中减去向量 ${\overrightarrow {a}}$ 与将 $(-{\overrightarrow {a}})$ 加到 ${\overrightarrow {b}}$ 是相同的。看一下以下向量减法的示例。

标量乘法

当您将向量乘以标量（普通数字）时会发生什么？

回到正常的乘法，我们知道 $2\times 2$ 只是 2 组 2 相加得到 4。我们可以采用类似的方法来理解向量乘法是如何工作的。