分形/计算机图形技术/2D/网格

数字区域边界追踪 - 起点

该域已被离散化为网格，然后光栅化为图像

图像

数字图像

• 二进制图像（1 位颜色）
• 灰度图像
• 彩色图像

• 
  二进制（1 位）图像
• 
  8 位灰度图像
• 
  24 位彩色图像

网格

• 网格
• 平铺
• 平面的镶嵌
  • 集合划分
• 格点
• 网格
• 棋盘格

另见

• 标尺
• 轴

维度

• 2D
• 3D

多边形 3D 网格的元素

类型

对网格进行分类是根据它们的网格基本元素：

• 规则网格 = 结构化网格 = 全局网格（有限差分）
  • 四边形网格在结构化网格中最常见
    • 二次 = 矩形网格
  • 三角网格：三角形是绘制各种网格和形状的最基本和标准方法之一
    • "考克斯特-弗鲁登塔尔三角剖分。它是通过使用均匀的立方网格划分空间来构建的，三角剖分是通过细分每个立方体得到的。"
  • 六边形
• 非结构化 = 不规则网格、自适应网格、局部网格（快速行进方法）。网格细化 = 自适应网格
  • 四叉树网格
  • BSP 树
  • 三角形曲面网格始终快速且易于创建。它在非结构化网格中最常见。
  • 空间自适应斐波那契网格

• 
  基本 2D 单元形状
• 
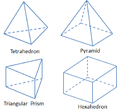
  基本 3D 单元形状

通过规则多边形进行平铺：规则（= 结构化）网格

• 
  三角形：考克斯特-弗鲁登塔尔三角剖分
• 
  二次
• 
  六边形平铺

三角剖分

• 曲面三角剖分
• commons 中的分类：三角剖分 (几何)
• 维基百科中的分类：三角剖分 (几何)
• 维基教科书中的德劳内三角剖分
• CONREC - 由 Paul Bourke 于 1987 年 7 月编写的等高线子程序（使用三角剖分） - 以规则的三角形网格表示的曲面
• delaunator - 用于对 2D 点进行德劳内三角剖分的超快速 JavaScript 库

• 
  用三角形表示的海豚插图。
• 
• 

应用

• 对于变形图像，德劳内三角剖分提供了一种“好”的方法，可以从要移动的点创建三角形网格。每个三角形都可以以简单的方式扭曲，从而导致整个图像发生复杂的“变形”扭曲。在所示的变形示例中，三角形形状从一个图像扭曲到另一个图像，例如，第一个图像中的头发被扭曲以适应第二个图像中的头发。与此同时，颜色从一种颜色“交叉淡入”到另一种颜色，因此灰色交叉淡入棕色。

内华达山脉地形图	2D 三角形网格	从网格计算的 2D 解决方案

• 为了对给定一组采样点的地形或其他物体进行建模，德劳内三角剖分提供了一组不错的三角形，可以用作模型中的多边形。特别是，德劳内三角剖分避免了狭窄的三角形（因为它们与它们的面积相比具有较大的外接圆）。

• 德劳内三角剖分在许多其他应用中使用，其中形状必须被划分为三角形。结构中应力和应变的分析通常使用三角形网格完成。在上面的分析中，在最感兴趣的区域放置了更多点，以便在该区域获得更精细的更详细的分析。这也就是我们在变形图像时所做的 - 我们在想要对变形的精细细节进行最大程度控制的地方放置了更多点。如果你想把皱眉变成微笑，就在嘴周围放更多点，这样你就可以更容易地改变形状。

像素连通性

维基百科中的像素连通性

• 
  正方形 4 连通性
• 
  正方形 8 连通性
• 
  六边形 6 连通性

创建

• gnuplot

网格

网格是通过较小的离散单元来表示更大的几何域。

按单元类型分类

• 多边形网格是顶点、边和面的集合，这些集合定义了多面体对象的形状。
  • 面通常由三角形（三角形网格）组成
  • 四边形（四边形）
  • 简单的凸多边形（n 边形）

软件

• openmesh - 一种通用的、高效的多边形网格数据结构（C++）
• meshlab
• paraview
• 多边形网格处理库 是一个现代的 C++ 开源库，用于处理和可视化多边形曲面网格。 演示
• VCG 可视化和计算机图形库（简称 VCG）是一个开源的便携式 C++ 模板库，用于操作、处理和使用 OpenGL 显示三角形和四面体网格
• meshio 用于 python 中多种网格格式的输入/输出
• mesh pro 商业

维基百科中的网格生成

坐标系

在几何学中，坐标系是一个使用一个或多个数字（= 坐标）来唯一确定空间中一个点的位置的系统

参见

• 镶嵌是将空间划分为一组较小的多边形的过程。
• commons:Category:Mesh in computer graphics
• 维基百科: 网格单元拓扑
• 寻路
• 三角形带 是一系列连接的三角形，它们共享顶点，从而可以更有效地利用计算机图形的内存。
• 变换
• 光栅化
  • 维度感知光栅化
• 平面分解
• 平铺
  • 罗伯特·希顿：波函数坍缩算法