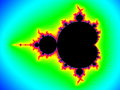
分形/扫描

扫描，采样

采样

• 从函数、映射、图像中获取有限数量的值的过程。^[1][2]
• 在统计学、质量保证和调查方法学中，抽样是从统计总体中选择个体子集（统计样本）以估计整个总体的特征。统计学家试图收集代表所讨论总体的样本。抽样比测量整个总体成本更低，数据收集速度更快，并且可以在无法测量整个总体的情况下提供见解。

分类标准:

• 遍数（单遍、多遍）
• 网格（规则=均匀/不规则或自适应）
• 随机（随机）/非随机
• 有分解或无分解

按范围划分的采样类型

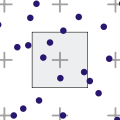
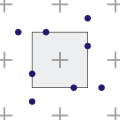
• 点采样=点采样方法。种子是一个定义的、有理复杂的数字，它代表一个像素=像素中心。请注意，可以在一个像素内找到无限多个点，而许多这样的点可能具有与像素中心不同的颜色/行为。
• 空间采样（样本之间发生了什么？）：一个手动定义的同质网格=均匀采样
• 1 像素近似=图像显示“平面上距离填充的朱利亚集至多为像素直径的点的集合”^[3]
  • 超采样^[4]=亚像素近似（分辨率）^[5]

按自适应划分的采样

• 规则、均匀（非自适应）采样
• 自适应（非均匀）采样=自适应网格细化 (AMR)
  • 基于梯度局部分形分析的细节增强：分形图像模型的关键概念是分形维数能够稳健地表示图像的内在结构信息。^[6][7]
  • 对复平面进行四叉树分解，并进行自适应细化，可以得到自适应近似
    • 自适应细分
    • “Mathematica 在需要时自动采样更多点以创建平滑的函数可视化”^[8]
    • 自适应采样用于精确绘制数学曲线^[9]

类型

• 标准扫描：一步渲染整个图像（以全分辨率）
• fractint 绘制方法
• 在每个后续细化步骤上进行圆形渲染

步骤

• 预览
• 最终渲染

按变换或平面类型（参数或动态）划分的类型

• 扫描标准 c 平面
• 扫描指数平面

标准

扫描平面

• 所有像素（平面逐像素扫描）一次通过
• 相同的像素大小（规则、均匀网格）

它还取决于平面描述

int SetPlane(complex double center, double radius, double a_ratio){

	ZxMin = creal(center) - radius*a_ratio;	
	ZxMax = creal(center) + radius*a_ratio;	//0.75;
	ZyMin = cimag(center) - radius;	// inv
	ZyMax = cimag(center) + radius;	//0.7;
    double PixelWidth = (ZxMax-ZxMin)/iWidth;
    double PixelHeight = (ZyMax-ZyMin)/iHeight; // pixel_size = PixelWidth = PixelHeight
	return 0;

}

角落

这里在Lisp

; common lisp. Here float values can be used,  there is no mapping
(loop for y from -1.5 to 1.5 by 0.1 do
      (loop for x from -2.5 to 0.5 by 0.05 do
            (princ (code-char 42))) ; print char
      (format t "~%")) ; new line

以及在C

/* c */
/* screen coordinate = coordinate of pixels */      
int iX, iY, 
iXmin=0, iXmax=1000,
iYmin=0, iYmax=1000,
iWidth=iXmax-iXmin+1,
iHeight=iYmax-iYmin+1;

/* world ( double) coordinate = parameter plane*/
const double ZxMin=-5;
const double ZxMax=5;
const double ZyMin=-5;
const double ZyMax=5;

/* */
double PixelWidth=(ZxMax-ZxMin)/iWidth;
double PixelHeight=(ZyMax-ZyMin)/iHeight;
double Zx, Zy,    /* Z=Zx+Zy*i   */
       Z0x, Z0y,  /* Z0 = Z0x + Z0y*i */

 for(iY=0;iY<iYmax;++iY)
      { Z0y=ZyMin + iY*PixelHeight; /* mapping from screen to world; reverse Y  axis */
        if (fabs(Z0y)<PixelHeight/2) Z0y=0.0; /* Zy = 0 is a special value  */    
        for(iX=0;iX<iXmax;++iX)
         {    /* initial value of orbit Z0 */
           Z0x=ZxMin + iX*PixelWidth;
          }
      }

由 Robert Munafo 完成的正常网格扫描绘图^[10]

  /* Plot a single pixel, row i and column j
 
   NOTE:
     itmax is the maximum number of Mandelbrot iterations
     min_r is the real coordinate of the left edge of the image
     max_i is the imaginary coordinate of the top of the image
     px_spacing = pixel size  is the width of the image (in real coordinates) divided by the number of pixels in a row
     image aspect ratio = 1:1
  */
  void pixel_53(int i, int j, int itmax)
  {
    double cr, ci;
 
    ci = max_i - ((double) i) * px_spacing;
    cr = min_r + ((double) j) * px_spacing;
    evaluate_and_plot(cr, ci, itmax, i, j);
  }

半径

  // modified code using center and radius to scan the plane 
  int height = 720;
  int width = 1280;
  double dWidth;
  double dRadius = 1.5;
  double complex center= -0.75*I;
  double complex c;
  int i,j;

  double width2; // = width/2.0
  double height2; // = height/2.0
  
  width2 = width /2.0;
  height2 = height/2.0;

complex double coordinate(int i, int j, int width, int height, complex double center, double radius) {
  double x = (i - width /2.0) / (height/2.0);
  double y = (j - height/2.0) / (height/2.0);
  complex double c = center + radius * (x - I * y);
  return c;
}

for ( j = 0; j < height; ++j) {
    for ( i = 0; i < width; ++i) {
      c = coordinate(i, j, width, height, center, dRadius);
      // do smth 
       }
     }

另一个版本

int main()
{
  int aa = 4;
  int w = 800 * aa;
  int h = 800 * aa;
  
  #pragma omp parallel for schedule(static, 1)
  for (int j = 0; j < h; ++j)
  {
    double y = (h/2 - (j + 0.5)) / (h/2) * r;
    for (int i = 0; i < w; ++i)
    {
      double x = (i + 0.5 - w/2) / (h/2) * r;
      double _Complex c = x + I * y;
      // proceed
    }
  }
  
  return 0;
}

平面分解

四叉树

四叉树类型

• 区域四叉树
• 点四叉树

• 距离估计，由 Claude Heiland-Allen 完成的 Koebe 1/4 定理
• 由 Mandrian 完成的快速曼德布罗集四叉树
• 由 Rico Mariani 完成的绘制曼德布罗集的 Mariani-Silver 算法
• 来自曼德布罗集词汇表和百科全书的 Mariani/Silver 算法，由 Robert Munafo 完成，(c) 1987-2022。
• openprocessing：由 Naoki Tsutae 完成的四叉树

• 
• 
• 
• 
  曼德布罗多线程
• 
• 
  迭代可视化
• 

// Quad-tree by Naoki Tsutae in Processing
// https://openprocessing.org/sketch/1769288
quadTree = (x, y, size) => {
 if (size < minRectSize) return;
 const n = noise((x + posx) * 0.001, (y + posy) * 0.001, variation);
 if (abs(n - 0.45) > size / maxRectSize) {
   rect(x, y, size);
 } else {
   size /= 2;
   const d = size / 2;
   quadTree(x + d, y + d, size);
   quadTree(x + d, y - d, size);
   quadTree(x - d, y + d, size);
   quadTree(x - d, y - d, size);
 }
};

区域四叉树

区域四叉树表示空间划分，通过将区域分解为四个相等的象限、子象限等等，每个叶节点包含与特定子区域相对应的数据。树中的每个节点要么具有

• 正好四个子节点
• 或者没有子节点（叶节点）。

遵循这种分解策略的四叉树的高度（即，只要在子象限中有感兴趣的数据，就细分子象限）对正在分解的空间中感兴趣区域的空间分布敏感且依赖于此。区域四叉树是一种trie。

深度为 n 的区域四叉树可用于表示包含 2ⁿ × 2ⁿ 个像素的图像，其中每个像素值均为 0 或 1。根节点表示整个图像区域。如果任何区域中的像素并非完全为 0 或 1，则将其细分。在此应用中，每个叶节点表示一个像素块，这些像素块均为 0 或 1。请注意，当这些树用于存储图像时，在空间方面可能会有潜在的节省；图像通常有许多大小可观的区域，在整个区域中具有相同的颜色值。与其存储图像中每个像素的二维数组，不如使用四叉树来捕获可能比我们否则需要像素分辨率大小的单元高出许多划分级别的相同信息。树分辨率和整体大小受像素大小和图像大小的限制。

区域四叉树还可以用作数据场的可变分辨率表示。例如，区域中的温度可以存储为四叉树，每个叶节点存储其表示的子区域的平均温度。

Koebe 四分之一定理:

Once b [the exterior distance estimate for c] is found, by the Koebe 1/4-theorem, we know there's no point of the Mandelbrot set with distance from c smaller than b/4. 

// code in Haskell by Claude Heiland-Allen https://mathr.co.uk/blog/2010-10-30_distance_estimation.html
exterior :: Square -> Bool
exterior s@(Square a b c d) = fromMaybe False $ do
  lb <- distance a
  lt <- distance b
  rb <- distance c
  rt <- distance d
  let k = 4 * sqrt 2 * size s
  return $ and
    [ lb + rb > k
    , lt + rt > k
    , lb + lt > k
    , rb + rt > k
    ]

抗锯齿和超采样

计算最终颜色值

超采样或超采样抗锯齿 (SSAA) 是一种空间抗锯齿方法，即用于从计算机游戏中渲染的图像或生成图像的其他计算机程序中消除锯齿（锯齿状和像素化边缘，俗称“锯齿”）的方法。锯齿的出现是因为与具有连续平滑曲线和线条的现实世界物体不同，计算机屏幕向观看者显示大量的小方块。这些像素大小相同，每个像素都有单一颜色。线条只能显示为像素集合，因此除非它是完全水平或垂直的，否则看起来会很锯齿。超采样的目的是减少这种效果。在像素内部的多个实例（而不仅仅是在中心，像正常情况一样）进行颜色采样，然后计算平均颜色值。这是通过以比要显示的分辨率高得多的分辨率渲染图像，然后将其缩小到所需大小，并使用额外的像素进行计算来实现的。结果是降采样的图像，在物体边缘的像素行之间具有更平滑的过渡。

样本数量决定了输出质量。

• TechInfo - 由 Michael Condron 提供的抗锯齿
• Fract (Lisp 代码) 由 Yannick Gingras 提供
• 维基百科上的空间抗锯齿
• 分形论坛讨论：分形的抗锯齿 - 最佳方法？

• 超级采样
• 
  超级采样图像示例
• 
  超级采样的 Cpp 代码
• 
  带锯齿的棋盘 - 图像和 C 源代码

超级采样，其他名称

• 抗粒几何
• 超级采样（下采样）
• 缩小尺寸
• 缩小比例
• 亚像素精度

计算成本和自适应超级采样

超级采样在计算上很昂贵，因为它需要更大的显卡内存和内存带宽，因为使用的缓冲区大小要大得多。 解决这个问题的一种方法是使用称为自适应超级采样的技术，它只对物体边缘的像素进行超级采样。

最初，每个像素内只取几个样本。如果这些值非常相似，则只使用这些样本确定颜色。如果不是，则使用更多样本。这种方法的结果是，只有在必要的地方才会计算更多样本，从而提高性能。

类型

在像素内取样时，必须以某种方式确定样本位置。虽然这样做的方法数量是无限的，但有一些方法是常用的。

• 
  均匀分布的网格算法
• 
  旋转网格算法（样本密度为 2 倍）
• 
  随机算法
• 
  抖动算法
• 
  泊松圆盘算法
• 
  准蒙特卡罗方法算法
• 
  N 皇后
• 
  RGSS
• 
  高分辨率抗锯齿 (HRAA)，五边形
• 
  翻转四边形
• 
  翻转三角形

网格

最简单的算法。像素被分成几个子像素，每个子像素的中心都会取一个样本。它快速且易于实现。但是，由于采样的规律性，如果使用的子像素数量较少，仍然会发生锯齿。

随机

也称为随机采样，它避免了网格超级采样的规律性。但是，由于模式的不规则性，样本在像素的某些区域会变得不必要，而在其他区域则会缺失。

泊松圆盘

• 
  使用泊松圆盘采样生成的点样本，以及最小点间距离的图形表示

泊松圆盘采样算法 将样本随机放置，然后检查任何两个样本是否过于接近。最终结果是均匀但随机的样本分布。但是，该算法所需的计算时间过长，不适合用于实时渲染，除非采样本身在计算上比样本点的定位更昂贵，或者样本点不会为每个像素重新定位。

Poisson-disk sampling (blue noise) is the best sampling pattern. It maximizes the uniformity of the samples in addition to the randomness of their placement, which gets you the most bang for your buck with respect to the contribution of each sample. quaz0r on FF

链接

• 由 christian 于 2017 年 4 月 22 日提供的 poisson-disc-sampling-in-python

抖动

对网格算法的修改，以近似泊松圆盘。像素被分成几个子像素，但样本不是从每个子像素的中心取的，而是从子像素内的随机点取的。聚集仍然可能发生，但程度较小。 抖动也被推荐用于避免莫尔纹。

旋转网格

使用 2×2 网格布局，但样本模式被旋转，以避免样本与水平或垂直轴对齐，这极大地提高了最常见情况下的抗锯齿质量。为了获得最佳模式，旋转角度为 arctan (1/2)（约 26.6 度），正方形被拉伸了${\frac {\sqrt {5}}{2}}$倍。

具有极端伪随机锯齿的图像示例

因为分形具有无限的细节，并且除了算术舍入误差之外没有噪声，所以它们比照片或其他测量数据更清晰地说明了锯齿。逃逸时间（它们在像素的精确中心转换为颜色）在集合的边界处趋于无穷大，因此，由于锯齿，靠近边界的中心的颜色是不可预测的。此示例在其大约一半的像素中都有边缘，因此它显示出许多锯齿。第一张图像以其原始采样率上传。（由于大多数现代软件都会进行抗锯齿处理，因此可能需要下载完整尺寸的版本才能看到所有锯齿。）第二张图像以五倍的采样率进行计算，然后使用抗锯齿进行下采样。假设人们真的想要每个像素的平均颜色，那么这张图像就更接近了。它明显比第一张图像更有序。

为了正确比较这些图像，有必要以全尺寸查看它们。

• 
  1. 使用程序“MandelZot”计算
• 
  2. 通过模糊和下采样五倍进行抗锯齿处理
• 
  3. 对边缘点进行插值，然后进行抗锯齿处理并进行下采样
• 
  4. 对从上一张图像中删除的点进行增强
• 
  5. 再次下采样，不进行抗锯齿处理

在这种情况下，碰巧有额外的信息可用。通过使用“距离估计器”算法重新计算，识别出了非常靠近集合边缘的点，因此，集合边缘附近快速变化的逃逸时间会将异常精细的细节混叠进来。从这些计算出的点得出的颜色已被识别为其像素的异常不具有代表性。集合在那里变化得更快，因此单个点样本不能代表整个像素。在第三张图像中，这些点被替换为周围点的插值。这减少了图像的噪点，但也有使颜色变亮的副作用。因此，此图像与通过更大的计算点集获得的图像不完全相同。为了显示被丢弃了什么，第四张图像显示了被拒绝的点，这些点被混合到灰色背景中。

最后，“发芽涡轮机”非常规则，因此在向下取样以获取最近的像素时，在主“涡轮轴”附近可以清楚地看到系统性的（莫尔）混叠。第一张图像中的混叠看起来是随机的，因为它来自像素大小以下的所有细节级别。当抑制较低级别的混叠以制作第三张图像，然后再次对第三张图像进行降采样（无抗锯齿）以制作第五张图像时，第三张图像尺度上的顺序在第五张图像中表现为系统性的混叠。

图像的纯降采样具有以下效果（建议全尺寸查看）

• 
  1) Mandelbrot 集合 的特定螺旋特征的图片
• 
  2) 每个像素 4 个样本
• 
  3) 每个像素 25 个样本
• 
  4) 每个像素 400 个样本

代码

• 由 用户 Geek3 编写的 Cpp 代码

 // subpixels finished -> make arithmetic mean
 char pixel[3];
 for (int c = 0; c < 3; c++)
   pixel[c] = (int)(255.0 * sum[c] / (subpix * subpix)  + 0.5);
 fwrite(pixel, 1, 3, image_file);
 //pixel finished

• Ned Batchelder 的 Aptus 命令行版本（python 和 c 代码）（参见 aptuscmd.py）使用通过 PIL 函数 resize 的高质量降采样滤波器
• Josef Jelinek 编写的 Java 代码: 使用网格算法进行超采样，计算 4 个新点（角点），产生的颜色是每个颜色分量的平均值

 //Created by Josef Jelinek
 // http://java.rubikscube.info/
 Color c0 = color(dx, dy); // color of central point
 // computation of 4 new points for antialiasing
 if (antialias) { // computes 4 new points (corners)
   Color c1 = color(dx - 0.25 * r, dy - 0.25 * r);
   Color c2 = color(dx + 0.25 * r, dy - 0.25 * r);
   Color c3 = color(dx + 0.25 * r, dy + 0.25 * r);
   Color c4 = color(dx - 0.25 * r, dy + 0.25 * r);
  // resulting color; each component of color is an avarage of 5 values (central point and 4 corners)
   int red = (c0.getRed() + c1.getRed() + c2.getRed() + c3.getRed() + c4.getRed()) / 5;
   int green = (c0.getGreen() + c1.getGreen() + c2.getGreen() + c3.getGreen() + c4.getGreen()) / 5;
   int blue = (c0.getBlue() + c1.getBlue() + c2.getBlue() + c3.getBlue() + c4.getBlue()) / 5;
   color = new Color(red, green, blue);
 }

• 可以创建大图像（例如 10 000 x 10 000），并将其转换/调整大小（缩小）。例如使用 ImageMagick

convert big.ppm -resize 2000x2000 m.png

降采样和插值本质上是压缩，低频分量，即

• 变化速度低于采样频率一半的缓慢变化颜色将被保留
• 高频细节将丢失

区间算术

• 用于生成有保证的 Julia 集合图像的自适应算法
• 真实形状算法 (TSA)

如何优化搜索最近的点？

• gamedev.stackexchange 问题：如何优化搜索最近的点？

另请参阅

• Tessellation 是将空间划分为一组较小多边形的过程
• 2D 网格类型
• commons:Category:Mesh in computer graphics
• 采样和图像噪声 - dither 用于更准确地显示包含比显示硬件能够显示的更大范围颜色的图形
• Fractint 绘制方法
• Steven Stoft 编写的 Fratal Witchcraft 绘制方法
• AlmondBread 算法
• rugh 集方法
• 细胞映射 基于区间算术，在图中使用标签传播以避免函数迭代和舍入误差
• “我们将基于区间算术的细胞映射与图中的标签传播相结合，以避免函数迭代和舍入误差。” - Luiz Henrique de Figueiredo 等人
• 使用外部距离估计 和 Koebe 四分之一定理
• 使用 对称

参考资料

• Serious Statistics: The Aliasing Adventure By Guest_Jim March 17, 2019