分形/复平面上的迭代/花瓣
Leau-Fatou 花的花瓣

"花瓣...有趣之处不仅在于它们对抛物点附近出现的动力学提供了相当直观的理解,而且在于 f0 在花瓣上的动力学可以线性化,即它与由 T(w) := w + 1 定义的 C 的位移映射 T 共轭。"(Laurea Triennale[1])
- 花瓣没有统一的定义
- "花瓣是 不变的约旦域"(R PEREZ-MARCO[2] (其中 q 是子周期。并且抛物线 c 参数是曼德布罗特集的父组件和子组件之间的根点)
- 花瓣是陷阱,它捕获任何趋向于抛物点的轨道
- 花瓣是花的一部分
花的花瓣可以是
- 吸引/排斥
- 小/α/大/(小的吸引花瓣与排斥花瓣不重叠,但大的则重叠)
每个花瓣在 f^周期下是不变的。换句话说,它被 f^周期映射到自身。
吸引花瓣 P 是
- 每个花瓣在 下是不变的。换句话说,它被 映射到自身:
- 域 (拓扑圆盘) 包含
- 抛物周期点 p 在其边界 (精确地在其根部,它是所有吸引花瓣和排斥花瓣的公共点 = Lea-Fatou 花的中心)
- 临界点或其在另一侧的 n=周期像 (仅小的?)
- 陷阱 捕获任何趋向于抛物点的轨道[3]
- 包含在填充的 Julia 集的组件内的集合。抛物固定点的吸引花瓣包含在其吸引盆中
- "... 就该属性而言,它最大。这个首选花瓣 P max 始终在其边界上有一个或多个临界点。"[4]
- "吸引花瓣是完全位于 Fatou 集中的解析曲线的内部,在固定点处具有正确的切线性质,并且被映射到其内部,通过映射的正确幂" Scott Sutherland
- "... 吸引花瓣是周期点周围足够小的圆盘中的一组点,它们的正向轨道在返回映射的幂下始终保留在圆盘内。" (W P Thurston: 关于迭代有理映射的几何和动力学)
花瓣 关于 d-1 方向 是对称的
在哪里
- d 是 (待做)
- l 从 0 到 d-2
花瓣可以有不同的尺寸。
如果 ,那么 Julia 集应该在 n 个方向上接近抛物周期点,在 n 个花瓣之间。 [5]
"用全纯动力学的语言来说,人们会说你正在研究多项式在抛物线不动点 附近的动力学。通过一个简单的线性变量变换,任何这样的抛物线不动点的研究都可以简化为对 的研究。然后你可以应用另一个变换 。因此,你被简化为对 的研究。如果实部 $Re(w)$ 足够大,你将得到 。这将给你你想要的东西(当你回到 z 变量时)。
区域 (对于较大的 )看起来像某种心形(在你的特定情况下)当你把它可视化在 z 变量中(它被诗意地称为吸引花瓣)。 Sylvain Bonnot[6]
构造花瓣
[edit | edit source]
陷阱参数
- 形状
- 中心
- 大小
子周期分量的目标集
- 1 和 2 目标集可以是圆,抛物线不动点位于其边界上(目标集位于分量内部)。
- 对于周期 3 及更高(p > 2),目标集是中心在抛物线不动点处的圆的三角形片段。
- 按周期划分的分量的目标集
-
p=1 圆形
-
p=2 圆形
-
p>2。三角形。这里目标集很窄,所以未定义点是可见的。
-
p = 11 的射线和临界轨道
- 分量陷阱:三角形
- BDM 陷阱:三角形
在哪里
- z1、z2 是边界分量的外部射线的最后一点(通常是最大的一个,临界点在其中)。
- 是临界点,或者如果临界轨道臂不是直线,则它是它的前向像。
- 是抛物线不动点。
- 是一个前临界点 = 临界点的原像。
由于动力学延迟,计算在临界轨道和外部射线落在抛物线不动点之前停止。剩余的间隙用从最后一点到着陆点的线填充(近似)。
-
计算和近似部分
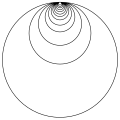
0/1 或 1/1
[edit | edit source]-
它是 fc(z)=z^2 + 1/4 的动态平面。它是围绕抛物线不动点 z=0.5 的缩放。显示了 Julia 集内部某些点的轨道(白色点)。
-
吸引花瓣(灰色)
-
抛物线不动点附近的动力学
-
1 花瓣花(偶极子)内部动力学的连续模型
第一个吸引花瓣是一个圆,它具有
- 中心位于 x 轴上
- 半径 = (cabs(zf) + cabs(z))/2
其他(更大的)吸引花瓣是第一个花瓣的前像,其中包括第一个花瓣。
在哪里
- z 是临界轨道的最后一点。
- zf 是一个不动点。
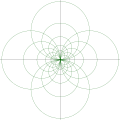
1/2
[edit | edit source]-
2 花瓣花(四极子)内部动力学的模型
-
点状四极子场的等势面的等高线图
圆形吸引花瓣
- 中心位于定点和临界点之间。
- 半径小于定点和临界点之间距离的一半。
// choose such value that level sets cross at z=0
// choose radius such a
double GivePetalRadius(complex double c, complex double fixed, int n){
complex double z = 0.0; // critical point
int k;
// best for n>1
int kMax = (n*ChildPeriod) - 1; // ????
for(k=0; k<kMax-1; ++k)
z = z*z + c; // forward iteration
return cabs(z-fixed)/2.0;
}
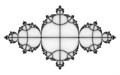
1/3
[edit | edit source]-
胖杜瓦迪兔子朱利亚集的定点附近的轨道
斯科特·萨瑟兰的方法:[7]
- 选择包含临界点的连通分量
- 找到一条完全位于法图集内的解析曲线,在定点处具有正确的切线性质,并且被映射到其内部的正确映射幂次
- 另外两个只是这条曲线在第一次和第二次迭代下的图像。
其他情况
[edit | edit source]-
1/30
花瓣数量
[edit | edit source]| 此页面上次编辑于 18 个月前,可能已被弃用 此页面自 2023 年 3 月 18 日起未被编辑,但本书中的其他页面可能已被编辑。查看相关更改以查看本书的当前状态。 您可以通过编辑和更新本书来提供帮助。如果此页面没有被积极编辑,请删除 {{under construction}}。在WB:PROJECTS中寻求帮助。 |

对于二次多项式
重数 = 父周期 + 子周期
花瓣数量 = 重数 - 父周期
这是因为在抛物情况下,定点与周期循环重合。循环的长度(子周期)等于花瓣的数量。
对于其他多项式映射
-
一个临界点和 5 个花瓣
-
13 个临界点和 26 个花瓣。
-
14 个临界点和 14 个花瓣。
-
z^4-z 有 3 个临界点和 6 个花瓣
| f(z) | 花瓣数量 | 解释 |
|---|---|---|
| d-1 | 对于 点 z=0 的重数为 d | |
| d+2 | (?)对于 根 z=0 的重数为 d+3 | |
对于 f(z)= -z+z^(p+1) 抛物花具有
- 2p 个花瓣,当 p 为奇数时
- p 个花瓣,当 p 为偶数时[8]
... (待办事项)