复数有理函数的迭代^[1]^[2]^[3]

示例

牛顿分形
commons:Category:Complex rational maps
Suzanne Boyd 和 Alexander J. Mitchell 在 2023 年发表的“Generalized McMullen Maps 的有界性轨迹和婴儿 Mandelbrot 集”
马克·麦克卢尔：黎曼球面上的一个 Julia 集
f(z)=z2/(z9-z+0,025) ^[4]
f(z)=(z3-z)/(dz2+1)，其中 d=-0,003+0,995i ^[5]
f(z)=(z3-z)/(dz2+1)，其中 d=1,001· e2Pi/30 ^[6]
Xender 的 Multibrot 集^[7]
$f_{\lambda }(z)=z^{n}+{\frac {\lambda }{z^{d}}}$ ^[8]
马克·麦克卢尔的 Rational Julia Sets
f(z) = (z^n+c)/(c^n+z)，对于 n = -2 ^[9]
Jasper Weinrich Burd：气泡浴 Julia 集的 Thompson 类群
安德斯·桑德伯格在 2004 年发表的“鲍鱼分形”
(z2-1)/(z2+1)。它在 ±1 处有简单的零点，在 ±i 处有简单的极点。
Shigehiro Ushiki = ComplexExplorer 页面
沃尔夫·荣格的“具有超吸引 2 周期的有理映射”
胡军和 Arkady Etkin 的“具有逃逸临界点的三次有理映射的 Julia 集”
骆育生在 2021 年发表的“关于具有有限连接 Fatou 集的双曲有理映射”
骆育生在 2021 年发表的“关于几何有限退化 I：主要双曲分量的边界”
骆育生在 2021 年发表的“关于几何有限退化 II：收敛和发散”
math.stackexchange 问题：如何计算负 Multibrot 集
尤尔根·迈尔的“奇异 Julia 集”
存在 Julia 集为整个平面的有理函数。第一个例子由 Lattès 给出： $R(z)={\frac {(z^{2}+1)^{2}}{4z(z^{2}-1)}}$ ^[10]
邱维元、杨飞、尹永成的“Julia 集为 Cantor 圆的有理映射”
Petersen, C. L. 和 S. Zakeri。“关于具有 Siegel 圆盘的典型二次多项式的 Julia 集”。《数学年鉴》，第 159 卷，第 1 期，2004 年，第 1-52 页。
沈亮、吴盛建的“关于具有两个 Siegel 圆盘的二次有理映射的注记”。《中国科学数学》（英文版）。2010 年 7 月，第 26 卷，第 7 期，第 1393-1402 页。在线发表日期：2010 年 6 月 15 日。DOI：10.1007/s10114-010-6611-3 Http://www.ActaMath.com
克里斯·金的“Mandelbrot 映射”
fractalforums.org : z-plus-c2-z3-plus-c $f(z)={\frac {\left(z+c\right)^{2}}{z^{3}+c}}$

图库

有理函数
${\frac {z}{z-1}}$
${\frac {z^{2}}{z^{2}-1}}$
${\frac {z^{3}}{z^{3}-1}}$
${\frac {z^{4}}{z^{4}-1}}$
${\frac {z^{5}}{z^{5}-1}}$
${\frac {z^{7}}{z^{7}-1}}$

有理函数
${\frac {z^{4}+0.05}{z^{4}-1}}$

${\frac {z^{3}}{z^{5}-1}}$
${\frac {z^{4}}{z^{5}-1}}$
${\frac {z^{5}}{z^{5}-1}}$
${\frac {z^{6}}{z^{5}-1}}$
${\frac {z^{7}}{z^{5}-1}}$

${\frac {(z-4i+3)(z-2-3i)z}{(z+2i+4)(z+3i-2)}}$

Blaschke 分式

对临界点的分析

kill(all);
remvalue(all);
display2d:false;
ratprint : false; /* remove "rat :replaced " */



rho : -0.6170144002709304 +0.7869518599370003*%i;

define(f(z), rho * z^2 * (z-3)/(1-3*z));

/* first derivativa wrt z */
define( d(z), diff(f(z),z,1));


/* hipow does not expand expr, so hipow (expr, x) and hipow (expand (expr, x)) may yield different results */
n : hipow(num(expand(f(z))),z);
m : hipow(denom(expand(f(z))),z);

/* check if infinity is a fixed point */
limit(f(z),z,infinity);



/* finite critical points */

s:solve(d(z)=0)$
s : map(rhs,s)$
s : map('float,s)$
s : map('rectform,s)$

所以有 3 个临界点

2 个有限临界点：z=1.0 和 z= 0.0
无穷大

动力学平面包含 3 个吸引域

吸引不动点 z = 无穷大（超吸引）的吸引域，有无数个连通分支
吸引不动点 z = 0（超吸引）的吸引域，有无数个连通分支
抛物型 3 周期循环的吸引域（其中 z= 1 为临界点）

有限 Blaschke 积

$B_{n}(z)$ 是一个 n 次有限 Blaschke 积。^[11] 它是一个：^[12]

有理函数
在开单位圆盘上的解析函数，使得 *f* 可以扩展到闭单位圆盘上的连续函数，该函数将单位圆映射到自身
在开单位圆盘内没有极点
特别地，如果 *ƒ* 满足上述条件，并且在单位圆内没有零点，那么 *ƒ* 为常数（这一事实也是最大值原理（应用于谐函数 log(|*ƒ*(*z*)|)）的推论）。
Blaschke 积 B 是圆盘倍增映射 R(z) = z^2 （等价于 θ → 2θ (mod 1)）的有理扰动。
一个有限 Blaschke 积可以通过其临界点集唯一地描述
使圆盘固定的有理映射 = 使闭单位圆盘 D 映射到自身的映射
它们的迭代理论可以从 Fuchsian 群的角度进行分析。
双曲平面上的多项式 = 双曲多项式
一个有限 Blaschke 积，限制在单位圆上，是一个光滑的覆盖映射
单位圆盘 D、单位圆 ∂D 和闭单位圆盘补集 C\D 都是 B 的完全不变集

B_{n}(z)=\zeta \prod _{i=1}^{n}\left({{z-a_{i}} \over {1-{\overline {a_{i}}}z}}\right)^{m_{i}}

其中

$\zeta$ 是一个模为 1 的常数。它是一个位于单位圆上的点： $|\zeta |=1$
$m_{i}$ 是零点的重数 $a_{i}$
$(a_{i})_{i=1}^{n}$ 是开单位圆盘 $|a_{i}|<1$ 中 n 个点的有限序列。

(a_{i})_{i=1}^{n}=(a_{1},a_{2},\ldots ,a_{n}).

Blaschke 积的构建块^[13] 是以下形式的 Möbius 变换：

$b_{k}(z)=e^{i\theta k}{\frac {a_{k}-z}{1-{\overline {a_{k}}}z}}$

其中

ak ∈ D := {z ∈ C|, |z| < 1}
θk ∈ R.

有限（无限）Blaschke 积具有以下形式：

$w=B(z)=\prod _{k=1}^{n}b_{k}(z)$

示例

Curtis T McMullen 的二次有理映射

分类

类似于 Möbius 变换，有限 Blaschke 积存在一个分类。^[14]

如果 B 的 Denjoy-Wolff 点 z0 位于 D 中，则 B 为椭圆型。|B' (z0)| < 1.
如果 B 的 Denjoy-Wolff 点 z0 位于 ∂D 上且 B'(z0) < 1，则 B 为双曲型。
如果 B 的 Denjoy-Wolff 点 z0 位于 ∂D 上且 B'(z0) = 1，则 B 为抛物型。

B 的 **Denjoy-Wolff 点** 是唯一的 z0 ∈ D，使得 $B^{n}(z)\to z_{0}$ 对于所有 z ∈ D 成立。

Julia 集

令 B 为度数为 d > 1 的有限 Blaschke 积。Julia 集 $J_{B}$ ，即迭代 $B^{n}$ 在任何邻域上不正常的集合，要么是单位圆 $S^{1}$ ，要么是 Cantor 子集^[15] ^[16]

如果 B 为椭圆型，则 J(B) = ∂D，
如果 B 为双曲型，则 J(B) 是 D 的 Cantor 子集，
如果 B 为抛物型，并且 z0 ∈ ∂D 是 B 的 Denjoy-Wolff 点，
- 如果 B(z0) = 0 ，则 J(B) = ∂D
- 如果 $B''(z0)\neq 0.$ ，则 J(B) 是 ∂D 的 Cantor 子集。

BDM 的边界

临界轨道

McMullen 映射

奇异扰动映射，也称为 McMullen 映射^[17]

  $R_{\lambda }(z)=z^{m}+\lambda /z^{d}$

度数 2

反向 Basilica Julia 集

函数： $f(z)={\frac {z^{2}}{z^{2}-1}}$

maxima

Maxima 5.41.0 http://maxima.sourceforge.net
using Lisp GNU Common Lisp (GCL) GCL 2.6.12
Distributed under the GNU Public License. See the file COPYING.
Dedicated to the memory of William Schelter.
The function bug_report() provides bug reporting information.
(%i1) display2d:false;

(%o1) false
(%i2) f:z^2/(z^2-1);

(%o2) z^2/(z^2-1)
(%i3) dz:diff(f,z,1);

(%o3) (2*z)/(z^2-1)-(2*z^3)/(z^2-1)^2
(%i4) s:solve(f=z);

(%o4) [z = -(sqrt(5)-1)/2,z = (sqrt(5)+1)/2,z = 0]
(%i5) s:map('float,s);

(%o5) [z = -0.6180339887498949,z = 1.618033988749895,z = 0.0]
(%i6)

因此，不动点 $z:f(z)=z$

z = -0.6180339887498949
z = 1.618033988749895
z = 0.0

泡泡浴 Julia 集

二次有理函数 f

f(z)={\frac {1-z^{2}}{z^{2}}}

关于 z 的导数为

f'(z)={\frac {-2}{z^{3}}}

f 的 Julia 集被称为泡泡浴 Julia 集。 ^[18] 它被称为泡泡浴，因为它在视觉上与一桶泡泡相似。

函数 f 在黎曼球面上的所有 z 中都有定义 ${\hat {\mathbf {C} }}$ = 它在整个黎曼球面上定义

f:{\hat {\mathbf {C} }}\to {\hat {\mathbf {C} }}

f 的 Fatou 集是 3 循环的吸引盆，该 3 循环由点 0、-1 和无穷大组成。它是唯一一个吸引循环，并且是超吸引循环
Julia 集 J(f) 是其轨道不被吸引到上述 3 循环的点的集合
f 的唯一临界点是
- z = 0，因为它是 d(z) 的 3 阶极点，是 1/d(z) 的零点
- z = 无穷大，因为它是函数 d(z) 的零点

Maxima CAS 代码

kill(all);
remvalue(all);
display2d:false;

define(f(z), (1 -z^2)/(z^2));

(%o3) f(z):=(1-z^2)/z^2
define( d(z), ratsimp(diff(f(z),z,1)));

(%o13) d(z):=-2/z^3
(%i14) limit(d(z),z,infinity);

(%o14) 0
(%i15) limit(d(z),z,0);

(%o15) infinity

(%i2) f(-1);
(%o2)                                  0
(%i3) limit(d(z),z,0);
(%o3)                             limit  d(z)
                                  z -> 0
(%i4) limit(f(z),z,0);
(%o4)                                 inf
(%i5) limit(f(z),z,inf);
(%o5)                                 - 1

周期循环的稳定性

kill(all);
display2d:false;
ratprint : false; /* remove "rat :replaced " */


define(f(z), (1 -z^2)/(z^2));

F(z0):= block(
	[z],
	if is(z0 = 0) then 	z: limit(f(z),z,0)
	elseif is(z0 = infinity) then z: limit(f(z),z,infinity)
	elseif is(z0 = inf) then z: limit(f(z),z,inf)
	else z:f(z0),
	
	return(z)
)$

define( dz(z), ratsimp(diff(f(z),z,1)));

Dz(z0) := block(

	[m,z],
	if is(z0 = 0) then m: limit(dz(z),z,0)
	elseif is(z0 = infinity) then m: limit(dz(z),z,infinity)
	elseif is(z0 = inf) then m: limit(dz(z),z,inf)
	else m:dz(z0),
	
	return(m)

)$

GiveStability(z0, p):=block(
	[z,d],
	
	/* initial values */
	d : 1,
	z : z0,
	
	for i:1 thru p step 1 do (
	
		d : Dz(z)*d,	
		z: F(z)
		/*print("i = ", 0, "  d =",d, "  z = ", z)*/
	),
	
	return (cabs(d))
)$

GiveStability(-1,3);

另请参阅

Boettcher 映射

由 Michael Becker 编写的 2 次

1 个周期 4 盆

3 次

映射的组成部分 $f(z)=z-(z^{3}-1)/3z^{2}$ 包含吸引点，这些吸引点是 $z^{3}=1$ 的解。这是因为该映射是用于查找方程 $z^{3}=1$ 的解的牛顿-拉夫森公式。这些解自然必须是吸引不动点。

由 Michael Becker 编写的 3 次

1 个周期 2 盆

$f(z)={\frac {1}{z^{3}+z*(-3-3*I)}}$

2 个临界点：{ -0.4550898605622273*I -1.098684113467809, 0.4550898605622273*I+1.098684113467809}；两个临界点都趋向于周期循环。

只有一个吸引周期循环：周期 2 循环 = {0, 无穷大}。

整个平面（球面）是周期 2 循环（分为 2 个部分）的吸引盆。Julia 集是边界。

2 个周期 2 盆

仅 Julia 集
Julia 集、吸引盆、临界轨道、吸引循环

功能

  $f(z)={\frac {1}{z^{3}+a*z+b}}$

其中

a = 2.099609375
b = 0.349609375

衍生物

 d(z):=-(3*z^2+2.099609375)/(z^3+2.099609375*z+0.349609375)^2

临界点

  [-0.8365822085525526*%i,0.8365822085525526*%i]

也可以使用 Wolfram Alpha 检查

 solve (3*z^2+2.099609375)/(z^3+2.099609375*z+0.349609375)^2=0

结果

 z = ± (5/16)* i* sqrt(43/6))

这两个是 2 个有限临界点。

无穷大也是一个临界点，因为一阶导数的分母阶数严格大于分子阶数。在数值计算中，可以使用临界值（临界点的像）

  $f(\infty )=0$

有两个周期 2 循环

{ +0.4101296722285255 +0.5079485669960778*I , +0.4101296722285255 -0.5079485669960778*I };
{ +1.6890328811664648 +0.0000000000000000*I , +0.1147519899962205 +0.0000000000000000*I };

两个有限临界点都落入第一个循环。无穷大（或其像零）落入第二个循环（在水平轴上）

无穷大不是不动点

remvalue(all);
display2d:false;
define(f(z), 1/(z^3+ 2.099609375*z +  0.349609375));
(%i5)limit(f(z),z,infinity);
(%o5) 0
(%i6) limit(f(z),z,0);
(%o6) 2.860335195530726

5 次

作者：L. Javier Hernandez Paricio

有理映射 $h(z)={\frac {1+4z^{5}}{5z^{4}}}$ 有六个不动点

∞（排斥）
−0,809017 − 0,587785i
−0,809017 +0,587785i
0,309017 − 0,951057i
0,309017 + 0,951057i
1

与不动点（6= ∞）相关联的端点的盆地与牛顿-拉夫森数值方法应用于寻找方程 $z^{5}-1=0$ 的根时的吸引盆地相同。^[19]

degree 6

degree 6 函数 f 的 Julia 集 ^[20]

$f(z)=z^{2}{\frac {3-z^{4}}{2}}$

在以下位置有 3 个超吸引不动点

z = 0
z = 1
z = ∞

所有其他临界点都在 1 的反向轨道上。

如何计算迭代

z:x+y*%i;
z1:z^2*(3-z^4)/2;
realpart(z1);
((x^2−y^2)*(−y^4+6*x^2*y^2−x^4+3)−2*x*y*(4*x*y^3−4*x^3*y))/2
imagpart(z1);
(2*x*y*(−y^4+6*x^2*y^2−x^4+3)+(x^2−y^2)*(4*x*y^3−4*x^3*y))/2

使用 Maxima CAS 查找不动点

z1:z^2*(3-z^4)/2;
s:solve(z1=z);
s:float(s);

结果

[z=−1.446857247913871,z=.7412709105660023,z=−1.357611535209976*%i−.1472068313260655,z=1.357611535209976*%i−.1472068313260655,z=1.0,z=0.0]

检查根的重数

multiplicities;
[1,1,1,1,1,1]

 z1:z^2*(3-z^4)/2;
 s:solve(z1=z)$
 s:map(rhs,s)$
 f:z1;
 k:diff(f,z,1);
 define(d(z),k);
 m:map(d,s)$
 m:map(abs,m)$
 s:float(s);
 m:float(m);

结果：有 6 个不动点，其中 2 个是超吸引的 (m=0)，其余是排斥的 (m>1)

 [−1.446857247913871,.7412709105660023,−1.357611535209976*%i−.1472068313260655,1.357611535209976*%i−.1472068313260655,1.0,0.0]
 [14.68114348748323,1.552374536603988,10.66447061028112,10.66447061028112,0.0,0.0]

临界点

[%i,−1.0,−1.0*%i,1.0,0.0]

degree 9 作者：Michael Becker

参考文献

通过临界点描述 Blaschke 乘积作者：Oleg Ivrii，特拉维夫大学：视频，演示
mathoverflow 问题：finding-the-critical-points-of-a-degree-5-blaschke-product

另请参阅

[1] 复数多项式的 Julia 集及其计算机实现作者：CM Stroh

[2] Julia 集作者：Michael Becker.

[3] 具有抛物线不动点的有理映射族的动力学和分岔作者：R. HAGIHARA 和 J. HAWKINS

[4] (z)=z2/(z9-z+0,025) 作者：Esmeralda Rupp-Spangle

[5] (z)=(z3-z)/(dz2+1) 其中 d=-0,003+0,995i 作者：Esmeralda Rupp-Spangle

[6] (z)=(z3-z)/(dz2+1) 其中 d=1,001· e2Pi/30 作者：Esmeralda Rupp-Spangle

[7] 数字狂想曲作者：Xender

[8] 有理映射的 Julia 集作者：PAUL BLANCHARD，CUZZOCREO，ROBERT L. DEVANEY，DANIEL M. LOOK，ELIZABETH D. RUSSELL

[9] ractalforums：分形数学、混沌理论和研究> 一般讨论 > Do z-->z/c² or z-->z*c² create a fractal

[10] th.stackexchange 问题：relation-between-filled-julia-set-and-julia-set-of-a-rational-function?

[11] 有限 Blaschke 乘积：概述作者：Stephan Ramon Garcia，Javad Mashreghi，William T. Ross

[12] 二维 Blaschke 乘积的动力学作者：ENRIQUE R. PUJALS 和 MICHAEL SHUB

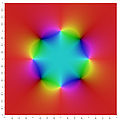
[13] Blaschke 乘积映射的彩色可视化作者：Cristina Ballantine 和 Dorin Ghisa

[14] 外摆线和 Blaschke 乘积作者：Chunlei Cao，Alastair Fletcher，Zhuan Ye

[15] 有限 Blaschke 乘积的收敛指数作者：Gavin L. Jones. Annales Academiæ Scientiarum Fennicæ Mathematica Volumen 22, 1997, 245–254

[16] Blaschke 乘积和参数空间作者：Katherine Plikuhn

[17] 有理映射的 Julia 集的对称性作者：Gustavo Rodrigues Ferreira

[18] 泡泡浴 Julia 集的类似汤姆森群作者：Jasper Weinrich-Burd，2013

[19] 外部离散半流：端点的盆地作者：L. Javier Hernandez Paricio，Miguel Maranon Grandes，M. Teresa Rivas Rodrıguez

[20] 关于 Thurston 的拉回映射作者：XAVIER BUFF，ADAM EPSTEIN，SARAH KOCH 和 KEVIN PILGRIM

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]