交通基础/路线选择

路线分配、路线选择或交通分配涉及在交通网络中选择起点和目的地之间的路线（称为路径）。它是传统的交通预测模型中的第四步，紧随出行生成、目的地选择和出行方式选择。出行分配的区域间交互分析提供了起点-目的地出行表。出行方式选择分析表明哪些出行者将使用哪种出行方式。为了确定设施需求以及成本效益，我们需要知道网络中每条路线和每条链路上的出行者数量（路线只是起点和目的地之间的一系列链路）。我们需要进行交通（或出行）分配。假设有一个公路和公共交通系统网络，以及一个拟议中的扩建项目。我们首先需要知道当前的出行时间和出行流量模式，然后是如果扩建项目完成会发生什么。

链路性能函数

驾驶员给其他人带来的成本被称为边际成本。然而，在做决定时，驾驶员只面对自己的成本（平均成本），而忽略了给其他人带来的任何成本（边际成本）。

$AverageCost=S_{T}/Q$
$MarginalCost=\delta S_{T}/\delta Q$

其中 $S_{T}$ 是总成本， $Q$ 是流量。

BPR链路性能函数

假设我们正在考虑一个公路网络。对于每条链路，都存在一个函数表明阻力与交通流量之间的关系。美国公共道路局 (BPR) 开发了一个链路（弧）拥塞（或流量-延迟，或链路性能）函数，我们将其称为S_a(Q_a)

$S_{a}\left({Q_{a}}\right)=t_{a}\left({1+0.15\left({\frac {Q_{a}}{c_{a}}}\right)^{4}}\right)\,\!$

t_a = 链路 a 的自由流出行时间，单位为时间

Q_a = 链路 a 上的交通流量（或体积），单位为时间（更准确地说：尝试使用链路 a 的流量）

c_a = 链路 a 的容量，单位为时间

S_a(Q_a) 是车辆在链路 a 上的平均出行时间

还有其他拥塞函数。CATS 长期使用与 BPR 不同的函数，但当比较 CATS 和 BPR 函数时，结果似乎没有太大差异。

流量可以超过容量吗？

在一条链路上，容量被认为是“流出”。需求是流入。

如果一段时间内流入 > 流出，就会出现排队（以及延误）。

例如，在 1 小时内，如果 2100 辆车到达，2000 辆车离开，那么还有 100 辆车仍在链路上。链路性能函数试图以一种简单的方式来表示这种现象。

沃德罗普的均衡原理

用户均衡

每个用户都采取行动来最小化自己的成本，前提是其他所有用户也这样做。所有使用路线的出行时间相同，并且低于任何未使用的路线的出行时间。

系统最优

每个用户都采取行动来最小化系统上的总出行时间。

无政府状态的价格

我们之所以出现拥塞，是因为人们是自私的。这种自私的成本（当人们根据自己的利益而不是社会的利益行事时）就是无政府状态的价格。

用户均衡条件下系统范围内的出行时间与系统最优条件下系统范围内的出行时间的比率。

无政府状态的价格 = $UE/SO>1$

对于具有线性链路性能函数（延迟函数）的双链路网络，无政府状态的价格小于4/3。

这是否过高？是否应该采取措施，或者33%的浪费是可以接受的？ [在其他情况下，在不同的假设下，损失可能更大/更小，等等。]

流量守恒

道路分配中一个重要的因素是流量守恒。这意味着在给定的时间段内，进入交叉路口（链路段）的车辆数量等于离开交叉路口的车辆数量（源点和汇点除外）。

类似地，进入链路后部的车辆数量等于离开前部的车辆数量（在很长一段时间内）。

自动分配

长期技术

以上示例适用于双链路问题，但实际网络要复杂得多。估计每条路线上的用户数量问题由来已久。随着高速公路和快速路（高速公路）的建设，规划者开始对此问题进行深入研究。高速公路比当地街道系统提供更优良的服务水平，并将交通从当地系统中转移出去。最初，转移是主要的技术。使用出行时间的比率，并辅以成本、舒适度和服务水平的考虑。

芝加哥地区交通研究 (CATS) 的研究人员开发了高速公路与当地街道的转移曲线。加州也做了很多工作，因为加州在高速公路规划方面有早期经验。除了转移类型的研究之外，CATS 还针对在处理复杂网络时出现的一些技术问题进行了研究。其中一项成果是用于查找网络上最短路径的摩尔算法。

转移方法无法处理的问题是链路和路线上的交通量对出行时间的影响。如果大量车辆试图使用某项设施，该设施就会变得拥挤，出行时间就会增加。在没有考虑反馈机制的情况下，早期的规划研究（实际上，大多数研究是在 1960 年至 1975 年期间）忽略了反馈。他们使用摩尔算法确定最短路径，并将所有交通分配到最短路径。这就是所谓的全或无分配，因为从 i 到 j 的所有交通都沿着某条路线行驶，或者根本不行驶。

从技术计算的角度来看，全或无或最短路径分配并非微不足道。每个交通区域都连接到 n-1 个区域，因此需要考虑许多路径。此外，我们最终关注的是链路上的交通流量。一条链路可能是几条路径的一部分，并且需要将沿着路径的交通流量逐链路相加。

可以提出一个支持全或无方法的论点。该论点如下：规划研究旨在支持投资，以便所有链路都提供良好的服务水平。使用与计划的服务水平相关的出行时间，计算结果表明改进到位后交通将如何流动。了解链路上的交通流量，就可以计算出满足所需服务水平所需的容量。

启发式程序

为了考虑交通负荷对出行时间和交通均衡的影响，开发了若干启发式计算程序。一种启发式方法按增量进行。要分配的交通量被分成几部分（通常为 4 部分）。分配第一部分交通量。计算新的出行时间，然后分配下一部分交通量。重复最后一步，直到分配完所有交通量。CATS 使用了该方法的变体；它按行分配 OD 表中的数据。

FHWA 收集的计算机程序中包含的启发式方法采用另一种方式。

步骤 0：首先使用全或无程序加载所有交通流量。
步骤 1：计算由此产生的出行时间，然后重新分配交通流量。
步骤 2：现在，开始使用权重进行重新分配。计算前两次加载中的加权出行时间，并将其用于下一次分配。最新的迭代获得 0.25 的权重，之前的迭代获得 0.75 的权重。
步骤 3. 继续进行。

这些程序似乎“运行良好”，但并不精确。

弗兰克-沃尔夫算法

Dafermos（1968）应用了弗兰克-沃尔夫算法（1956 年，Florian 1976），该算法可用于处理交通均衡问题。

均衡分配

为了将交通流量分配到路径和链路，我们必须制定规则，并且存在著名的沃德罗普均衡（1952 年）条件。这些条件的实质是，旅行者会努力寻找从起点到终点的最短（阻力最小）路径，并且当没有旅行者可以通过切换到新路径来减少出行努力时，就会发生网络均衡。这些被称为用户最优条件，因为一旦系统处于均衡状态，任何用户都不会从更改出行路径中获益。

用户最优均衡可以通过解决以下非线性规划问题来找到

$\min \sum _{a}{\int _{0}^{v_{a}}{S_{a}\left(Q_{a}\right)}}dx\,\!$

受制于

$Q_{a}=\sum _{i}{\sum _{j}{\sum _{r}{\alpha _{ij}^{ar}Q_{ij}^{r}}}}\,\!$

$\sum _{r}{Q_{ij}^{r}=Q_{ij}}\,\!$

$Q_{a}\geq 0,\;Q_{ij}^{r}\geq 0\,\!$

其中 $Q_{ij}^{r}\,\!$ 是从起点 i 到终点 j 的路径 r 上的车辆数量。因此，约束 (2) 表明所有旅行必须发生：i = 1 ... n; j = 1 ... n

$\alpha _{ij}^{ar}\,\!$ = 1 当且仅当链接 a 在从 i 到 j 的路径 r 上；否则为零。

因此，约束 (1) 对每个链接上的流量求和。网络上的每个链接都有一个约束。约束 (3) 确保没有负流量。

公共交通分配

也有一些方法被开发用来将乘客分配到公共交通工具。^[1]为了提高公共交通分配估计的准确性，通常会做出一些假设。这些假设的示例包括以下内容

所有公共交通出行都按照既定且预先定义的时间表运行，该时间表是已知的或对用户容易获得的。
公共交通服务（汽车/有轨电车/公交车容量）具有固定容量。^[2]

示例

示例 1

T问题

问题

如果链接 a 上的链接性能函数

$S_{a}=5+2*Q_{a}\,\!$

而链接 b 上的函数

$S_{b}=10+Q_{b}\,\!$

其中起点和终点之间的总流量为 1000 次旅行。求解两条并联链接的简单网络中链接 a 和 b 上的流量。

示例

解决方案

时间（成本）在所有使用过的路线中都相等，因此 $S_{a}=S_{b}$

我们还有流量守恒，因此 $Q_{a}+Q_{b}=Qo=Qd=1000$

$5+2*(1000-Q_{b})=10+Q_{b}$

$1995=3Q_{b}$

$Q_{b}=665;Q_{a}=335$

示例 2

T问题

问题

Eash、Janson 和 Boyce（1979 年）的一个示例将说明非线性规划问题的解决方案。从节点 1 到节点 2 有两条链接，每条链接都有一个阻力函数（参见图 1）。图 2 中曲线下的区域对应于公式 1 中从 0 到 a 的积分，它们加起来等于 220,674。请注意，链接 b 的函数是反方向绘制的。

$S_{a}=15\left({1+0.15\left({\frac {Q_{a}}{1000}}\right)^{4}}\right)\,\!$

$S_{b}=20\left({1+0.15\left({\frac {Q_{b}}{3000}}\right)^{4}}\right)\,\!$

$Q_{a}+Q_{b}=8000\,\!$

请用图形显示均衡结果。

示例

解决方案

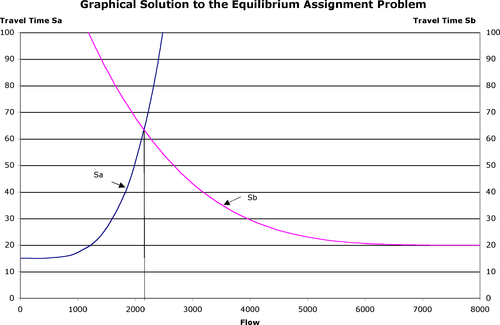
在均衡状态下，路线 *a* 上有 2152 辆车，路线 *b* 上有 5847 辆车。每条路线的旅行时间相同：大约 63 分钟。

图 3 说明了与均衡解不一致的车辆分配。曲线保持不变，但随着车辆在路线上的重新分配，阴影区域必须包含在解中，因此图 3 中的解比图 2 中的解大阴影区域的面积。

例 3

T问题

问题

Assume the traffic flow from Milwaukee to Chicago, is 15000 vehicles per hour. The flow is divided between two parallel facilities, a freeway and an arterial. Flow on the freeway is denoted  $Q_{f}$ , and flow on the two-lane arterial is denoted  $Q_{a}$ .

高速公路的旅行时间（以分钟计）（ $C_{f}$ ) 由下式给出

$C_{f}=10+Q_{f}/1500\,\!$

干线的旅行时间（ $C_{a}$ ) 由下式给出

$C_{a}=15+Q_{a}/1000\,\!$

应用沃德罗普的用户均衡原理，确定两条路线的流量和旅行时间。

示例

解决方案

旅行时间彼此相等

$C_{f}=C_{a}$

$10+Q_{f}/1500=15+Q_{a}/1000$

总交通流量等于 15000

$Q_{f}+Q_{a}=15000$

$Q_{a}=15000-Q_{f}$

$10+Q_{f}/1500=15+(15000-Q_{f})/1000$

求解 $Q_{f}$

$Q_{f}=60000/5=12000$

$Q_{a}=15000-Q_{f}=3000$

$C_{f}=18$

$C_{a}=18$

思考题

我们如何让驾驶员考虑他们的边际成本？
或者：我们如何让驾驶员以“系统最优”的方式行事？

示例问题

问题 (解答)
问题 (解答)

变量

$C_{T}$ - 总成本
$C_{k}$ - 路段 $k$ 的旅行成本
$Q_{k}$ - 路段 $k$ 的流量（体积）

缩略语

VDF - 交通量延迟函数
LPF - 路段性能函数
BPR - 公路局
UE - 用户均衡
SO - 系统最优
DTA - 动态交通分配
DUE - 确定性用户均衡
SUE - 随机用户均衡
AC - 平均成本
MC - 边际成本

关键词

路线分配，路线选择，汽车分配
交通量延迟函数，路段性能函数
用户均衡
系统最优
流量守恒
平均成本
边际成本

外部练习

使用 STREET 网站上的 ADAM 软件，尝试 Assignment #3，了解网络特征的变化如何影响路线选择。

其他问题

视频

参考文献

Dafermos, Stella. C. 和 F.T. Sparrow “一般网络的交通分配问题”。国家标准局研究杂志，73B，第 91-118 页。 1969 年。
Florian, Michael 编辑，交通均衡方法，施普林格出版社，1976 年。
Wardrop, J. C. “道路交通研究的某些理论方面”。土木工程师学会会刊第二部分，9，第 325-378 页。 1952 年
Eash, Ronald, Bruce N. Janson 和 David Boyce 均衡出行分配：实际应用的优势和意义，交通研究记录 728，第 1-8 页，1979 年。
Evans, Suzanne P. . “结合出行分配和路径分配的某些模型的推导和分析”。交通研究，第 10 卷，第 37-57 页，1976 年
Hendrickson, C.T. 和 B.N. Janson，“几种土木工程问题的通用网络流公式”。土木工程系统 1(4)，第 195-203 页，1984 年

进一步阅读

背景

[1] Spiess (1993) 基于最优策略的交通均衡分配

[2] Paolo Carraresi, Federico Malucelli, Stefano Pallottino (1995) 关于区域公共交通分配

[1]

[2]