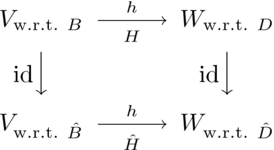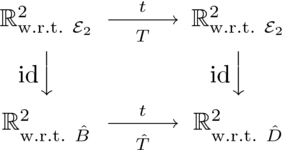线性代数/改变映射表示

线性代数
← 改变向量的表示	改变映射表示	投影 →

第一小节展示了如何将向量相对于一个基的表示转换为该向量相对于另一个基的表示。在这里我们将看到如何将映射相对于一对基的表示转换为该映射相对于另一对基的表示。也就是说，我们想要在这个箭头图中矩阵之间的关系。

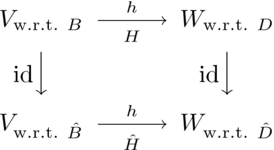
要从该图的左下角移动到右下角，我们可以直接向右移动，或者向上移动到 $V_{B}$ ，然后向右移动到 $W_{D}$ ，然后向下移动。用矩阵表示，我们可以计算 ${\hat {H}}={\rm {Rep}}_{{\hat {B}},{\hat {D}}}(h)$ ，要么简单地使用 ${\hat {B}}$ 和 ${\hat {D}}$ ，要么首先用 ${\rm {Rep}}_{{\hat {B}},B}({\mbox{id}})$ 改变基，然后乘以 $H={\rm {Rep}}_{B,D}(h)$ ，然后用 ${\rm {Rep}}_{D,{\hat {D}}}({\mbox{id}})$ 改变基。此等式总结了这一点。

{\hat {H}}={\rm {Rep}}_{D,{\hat {D}}}({\mbox{id}})\cdot H\cdot {\rm {Rep}}_{{\hat {B}},B}({\mbox{id}})\qquad \qquad (*)

(为了将这个等式与它前面的句子进行比较，请记住，这个等式是从右到左读的，因为函数组合是从右到左读的，而矩阵乘法代表组合。）

示例 2.1

矩阵

T={\begin{pmatrix}\cos(\pi /6)&-\sin(\pi /6)\\\sin(\pi /6)&\cos(\pi /6)\end{pmatrix}}={\begin{pmatrix}{\sqrt {3}}/2&-1/2\\1/2&{\sqrt {3}}/2\end{pmatrix}}

表示，关于 ${\mathcal {E}}_{2},{\mathcal {E}}_{2}$ ，变换 $t:\mathbb {R} ^{2}\to \mathbb {R} ^{2}$ ，它将向量 $\pi /6$ 弧度逆时针旋转。

我们可以将该表示形式相对于 ${\mathcal {E}}_{2},{\mathcal {E}}_{2}$ 转换为相对于

{\hat {B}}=\langle {\begin{pmatrix}1\\1\end{pmatrix}}{\begin{pmatrix}0\\2\end{pmatrix}}\rangle \qquad {\hat {D}}=\langle {\begin{pmatrix}-1\\0\end{pmatrix}}{\begin{pmatrix}2\\3\end{pmatrix}}\rangle

使用上面的箭头图和公式 ( $*$ )。

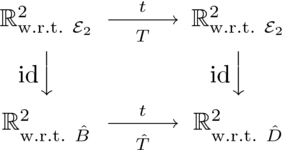
由此，我们可以使用公式

${\hat {T}}={\rm {Rep}}_{{\mathcal {E}}_{2},{\hat {D}}}({\mbox{id}})\cdot T\cdot {\rm {Rep}}_{{\hat {B}},{\mathcal {E}}_{2}}({\mbox{id}})$

注意 ${\rm {Rep}}_{{\mathcal {E}}_{2},{\hat {D}}}({\mbox{id}})$ 可以通过计算 ${\rm {Rep}}_{{\hat {D}},{\mathcal {E}}_{2}}({\mbox{id}})$ 的矩阵逆得到。

{\begin{array}{rl}{\rm {Rep}}_{{\hat {B}},{\hat {D}}}(t)&={\begin{pmatrix}-1&2\\0&3\end{pmatrix}}^{-1}{\begin{pmatrix}{\sqrt {3}}/2&-1/2\\1/2&{\sqrt {3}}/2\end{pmatrix}}{\begin{pmatrix}1&0\\1&2\end{pmatrix}}\\&={\begin{pmatrix}(5-{\sqrt {3}})/6&(3+2{\sqrt {3}})/3\\(1+{\sqrt {3}})/6&{\sqrt {3}}/3\end{pmatrix}}\end{array}}

虽然新矩阵看起来更乱，但它所代表的映射是相同的。例如，要复制 $t$ 在图片中的效果，从 ${\hat {B}}$ 开始，

{\rm {Rep}}_{\hat {B}}({\begin{pmatrix}1\\3\end{pmatrix}})={\begin{pmatrix}1\\1\end{pmatrix}}_{\hat {B}}

应用 ${\hat {T}}$ ，

{\begin{pmatrix}(5-{\sqrt {3}})/6&(3+2{\sqrt {3}})/3\\(1+{\sqrt {3}})/6&{\sqrt {3}}/3\end{pmatrix}}_{{\hat {B}},{\hat {D}}}{\begin{pmatrix}1\\1\end{pmatrix}}_{\hat {B}}={\begin{pmatrix}(11+3{\sqrt {3}})/6\\(1+3{\sqrt {3}})/6\end{pmatrix}}_{\hat {D}}

并与 ${\hat {D}}$ 进行比较

{\frac {11+3{\sqrt {3}}}{6}}\cdot {\begin{pmatrix}-1\\0\end{pmatrix}}+{\frac {1+3{\sqrt {3}}}{6}}\cdot {\begin{pmatrix}2\\3\end{pmatrix}}={\begin{pmatrix}(-3+{\sqrt {3}})/2\\(1+3{\sqrt {3}})/2\end{pmatrix}}

以查看它是否与上面的结果相同。

示例 2.2

在 $\mathbb {R} ^{3}$ 上，映射

{\begin{pmatrix}x\\y\\z\end{pmatrix}}{\stackrel {t}{\longmapsto }}{\begin{pmatrix}y+z\\x+z\\x+y\end{pmatrix}}

也就是说，它相对于标准基是这样表示的

{\rm {Rep}}_{{\mathcal {E}}_{3},{\mathcal {E}}_{3}}(t)={\begin{pmatrix}0&1&1\\1&0&1\\1&1&0\end{pmatrix}}

也可以用另一个基来表示

如果 $B=\langle {\begin{pmatrix}1\\-1\\0\end{pmatrix}},{\begin{pmatrix}1\\1\\-2\end{pmatrix}},{\begin{pmatrix}1\\1\\1\end{pmatrix}}\rangle$ 那么 ${\rm {Rep}}_{B,B}(t)={\begin{pmatrix}-1&0&0\\0&-1&0\\0&0&2\end{pmatrix}}$

以更简单的方式，即对角矩阵的作用很容易理解。

当然，我们通常更喜欢使表示更容易理解的基变。当相对于相同起始基和结束基的表示为对角矩阵时，我们说该映射或矩阵已 **对角化**。在第五章中，我们将看到哪些映射和矩阵是可对角化的，以及在不可对角化的情况下，我们将看到如何获得几乎对角化的表示。

我们本节最后考虑一个更容易的情况，即表示相对于可能不同的起始基和结束基。回想一下，上一节表明矩阵改变基当且仅当它是可逆的。这给了我们上面箭头图和方程的另一个版本 ( $*$ ).

定义 2.3

相同大小的矩阵 $H$ 和 ${\hat {H}}$ **矩阵等价**，如果存在可逆矩阵 $P$ 和 $Q$ 使得 ${\hat {H}}=PHQ$ .

推论 2.4

矩阵等价的矩阵表示同一映射，相对于适当的基对。

问题 10 检查矩阵等价是否是等价关系。因此它将矩阵集划分为矩阵等价类。

所有矩阵

H

矩阵等价
到

{\hat {H}}

通过将矩阵等价与行等价进行比较，我们可以对这些类别有所了解（回想一下，当矩阵可以通过行运算相互简化为彼此时，它们是行等价的）。在 ${\hat {H}}=PHQ$ 中，矩阵 $P$ 和 $Q$ 是非奇异的，因此每个都可以写成基本约简矩阵的乘积（见前一小节中的引理 4.8）。左乘构成 $P$ 的约简矩阵的效果是执行行运算。右乘构成 $Q$ 的约简矩阵执行列运算。因此，矩阵等价是行等价的推广——如果一个矩阵可以通过一系列行约简步骤转换为另一个矩阵，则两个矩阵是行等价的，而如果一个矩阵可以通过一系列行约简步骤后跟一系列列约简步骤转换为另一个矩阵，则两个矩阵是矩阵等价的。

因此，如果矩阵是行等价的，那么它们也是矩阵等价的（因为我们可以取 $Q$ 为单位矩阵，因此不执行任何列运算）。然而，反之则不成立。

示例 2.5

这两个

{\begin{pmatrix}1&0\\0&0\end{pmatrix}}\qquad {\begin{pmatrix}1&1\\0&0\end{pmatrix}}

是矩阵等价的，因为第二个可以通过将第一列乘以 $-1$ 并加到第二列的列运算简化为第一个。它们不是行等价的，因为它们具有不同的简化行梯形形式（事实上，两者都已经是简化形式）。

我们将通过为矩阵等价类找到一组代表来结束本节。^[1]

定理 2.6

任何 $m\!\times \!n$ 秩为 $k$ 的矩阵与 $m\!\times \!n$ 矩阵矩阵等价，该矩阵除了前 $k$ 个对角元素为 1 外，所有元素均为零。

{\begin{pmatrix}1&0&\ldots &0&0&\ldots &0\\0&1&\ldots &0&0&\ldots &0\\&\vdots \\0&0&\ldots &1&0&\ldots &0\\0&0&\ldots &0&0&\ldots &0\\&\vdots \\0&0&\ldots &0&0&\ldots &0\end{pmatrix}}

有时这被描述为块部分单位形式。

\left({\begin{array}{c|c}I&Z\\\hline Z&Z\end{array}}\right)

证明

如上所述，对给定矩阵进行高斯-约旦消元，并将所有用于消元的矩阵组合起来，形成 $P$ 。然后利用主元进行列消元，最后交换列，将主元置于对角线上。将用于这些列操作的消元矩阵组合成 $Q$ 。

示例 2.7

我们通过寻找此矩阵的 $P$ 和 $Q$ 来说明证明过程。

{\begin{pmatrix}1&2&1&-1\\0&0&1&-1\\2&4&2&-2\end{pmatrix}}

首先进行高斯-约旦行消元。

{\begin{pmatrix}1&-1&0\\0&1&0\\0&0&1\end{pmatrix}}{\begin{pmatrix}1&0&0\\0&1&0\\-2&0&1\end{pmatrix}}{\begin{pmatrix}1&2&1&-1\\0&0&1&-1\\2&4&2&-2\end{pmatrix}}={\begin{pmatrix}1&2&0&0\\0&0&1&-1\\0&0&0&0\end{pmatrix}}

然后进行列消元，这涉及到右乘。

{\begin{pmatrix}1&2&0&0\\0&0&1&-1\\0&0&0&0\end{pmatrix}}{\begin{pmatrix}1&-2&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{pmatrix}}{\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&1&1\\0&0&0&1\end{pmatrix}}={\begin{pmatrix}1&0&0&0\\0&0&1&0\\0&0&0&0\end{pmatrix}}

最后交换列。

{\begin{pmatrix}1&0&0&0\\0&0&1&0\\0&0&0&0\end{pmatrix}}{\begin{pmatrix}1&0&0&0\\0&0&1&0\\0&1&0&0\\0&0&0&1\end{pmatrix}}={\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&0&0\end{pmatrix}}

最后，将左乘子合并为 $P$ ，将右乘子合并为 $Q$ ，得到 $PHQ$ 方程。

{\begin{pmatrix}1&-1&0\\0&1&0\\-2&0&1\end{pmatrix}}{\begin{pmatrix}1&2&1&-1\\0&0&1&-1\\2&4&2&-2\end{pmatrix}}{\begin{pmatrix}1&0&-2&0\\0&0&1&0\\0&1&0&1\\0&0&0&1\end{pmatrix}}={\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&0&0\end{pmatrix}}

推论 2.8

两个相同大小的矩阵当且仅当它们具有相同的秩时，它们是矩阵等价的。也就是说，矩阵等价类由秩来刻画。

证明

两个具有相同秩的相同大小的矩阵等价于同一个块部分单位矩阵。

示例 2.9

$2\!\times \!2$ 矩阵只有三种可能的秩：零、一或二。因此，存在三个矩阵等价类。

所有 $2\!\times \!2$ 矩阵：三个等价
类

每个类包含所有具有相同秩的 $2\!\times \!2$ 矩阵。只有一个秩为零的矩阵，因此该类只有一个成员，但其他两个类分别具有无限多个成员。

在本小节中，我们已经看到了如何将映射相对于第一对基的表示更改为相对于第二对基的表示。这导致了一个定义，描述了矩阵在这种情况下何时是等价的。最后，我们注意到，通过适当选择（可能是不同的）起始和结束基，任何映射都可以用块部分单位形式表示。

这种表示形式的优点之一是，在某种意义上，当映射以这种方式表达时，我们可以完全理解映射：如果基是 $B=\langle {\vec {\beta }}_{1},\dots ,{\vec {\beta }}_{n}\rangle$ 和 $D=\langle {\vec {\delta }}_{1},\dots ,{\vec {\delta }}_{m}\rangle$ ，那么映射发送

c_{1}{\vec {\beta }}_{1}+\dots +c_{k}{\vec {\beta }}_{k}+c_{k+1}{\vec {\beta }}_{k+1}+\dots +c_{n}{\vec {\beta }}_{n}\;\longmapsto \;c_{1}{\vec {\delta }}_{1}+\dots +c_{k}{\vec {\delta }}_{k}+{\vec {0}}+\dots +{\vec {0}}

其中 $k$ 是映射的秩。因此，我们可以将任何线性映射理解为一种投影。

{\begin{pmatrix}c_{1}\\\vdots \\c_{k}\\c_{k+1}\\\vdots \\c_{n}\end{pmatrix}}_{B}\;\mapsto \;{\begin{pmatrix}c_{1}\\\vdots \\c_{k}\\0\\\vdots \\0\end{pmatrix}}_{D}

当然，要“理解”以这种方式表达的映射，我们需要了解 $B$ 和 $D$ 之间的关系。然而，尽管有这个困难，这仍然是一个对线性映射很好的分类。 }}

练习

此练习推荐所有读者完成。

问题 1

判断以下矩阵是否矩阵等价。

${\begin{pmatrix}1&3&0\\2&3&0\end{pmatrix}}$ , ${\begin{pmatrix}2&2&1\\0&5&-1\end{pmatrix}}$
${\begin{pmatrix}0&3\\1&1\end{pmatrix}}$ , ${\begin{pmatrix}4&0\\0&5\end{pmatrix}}$
${\begin{pmatrix}1&3\\2&6\end{pmatrix}}$ , ${\begin{pmatrix}1&3\\2&-6\end{pmatrix}}$

此练习推荐所有读者完成。

问题 2

求每个矩阵的矩阵等价类中的规范代表。

${\begin{pmatrix}2&1&0\\4&2&0\end{pmatrix}}$
${\begin{pmatrix}0&1&0&2\\1&1&0&4\\3&3&3&-1\end{pmatrix}}$

问题 3

假设关于

B={\mathcal {E}}_{2}\qquad D=\langle {\begin{pmatrix}1\\1\end{pmatrix}},{\begin{pmatrix}1\\-1\end{pmatrix}}\rangle

变换 $t:\mathbb {R} ^{2}\to \mathbb {R} ^{2}$ 由此矩阵表示。

{\begin{pmatrix}1&2\\3&4\end{pmatrix}}

使用基变换矩阵将 $t$ 表示为每对基。

${\hat {B}}=\langle {\begin{pmatrix}0\\1\end{pmatrix}},{\begin{pmatrix}1\\1\end{pmatrix}}\rangle$ , ${\hat {D}}=\langle {\begin{pmatrix}-1\\0\end{pmatrix}},{\begin{pmatrix}2\\1\end{pmatrix}}\rangle$
${\hat {B}}=\langle {\begin{pmatrix}1\\2\end{pmatrix}},{\begin{pmatrix}1\\0\end{pmatrix}}\rangle$ , ${\hat {D}}=\langle {\begin{pmatrix}1\\2\end{pmatrix}},{\begin{pmatrix}2\\1\end{pmatrix}}\rangle$

此练习推荐所有读者完成。

问题 4

在方程 ${\hat {H}}=PHQ$ 中， $P$ 和 $Q$ 的大小是多少？

此练习推荐所有读者完成。

问题 5

使用定理 2.6 来证明一个方阵是可逆的当且仅当它与单位矩阵等价。

此练习推荐所有读者完成。

问题 6

证明当 $A$ 是一个可逆方阵时，如果 $P$ 和 $Q$ 是可逆方阵，使得 $PAQ=I$ ，则 $QP=A^{-1}$ 。

此练习推荐所有读者完成。

问题 7

为什么定理 2.6 不能说明每个矩阵都是可对角化的（参见例 2.2）？

问题 8

矩阵等价矩阵是否一定具有矩阵等价的转置？

问题 9

如果 $k=0$ ，定理 2.6 会发生什么？

此练习推荐所有读者完成。

问题 10

证明矩阵等价是一个等价关系。

此练习推荐所有读者完成。

问题 11

证明零矩阵在其矩阵等价类中是唯一的。还有其他类似的矩阵吗？

问题 12

在 $\mathbb {R} ^{1}$ 和 $\mathbb {R} ^{3}$ 上的变换矩阵有哪些等价类？

问题 13

有多少个矩阵等价类？

问题 14

矩阵等价类在标量乘法和加法下是否封闭？

问题 15

设 $t:\mathbb {R} ^{n}\to \mathbb {R} ^{n}$ 由 $T$ 关于 ${\mathcal {E}}_{n},{\mathcal {E}}_{n}$ 表示。

在该特定情况下求 ${\rm {Rep}}_{B,B}(t)$ 。
$T={\begin{pmatrix}1&1\\3&-1\end{pmatrix}}\qquad B=\langle {\begin{pmatrix}1\\2\end{pmatrix}},{\begin{pmatrix}-1\\-1\end{pmatrix}}\rangle$
描述 ${\rm {Rep}}_{B,B}(t)$ 的一般情况，其中 $B=\langle {\vec {\beta }}_{1},\ldots ,{\vec {\beta }}_{n}\rangle$ 。

问题 16

设 $V$ 有基 $B_{1}$ 和 $B_{2}$ ，假设 $W$ 有基 $D$ 。设 $h:V\to W$ ，求计算 ${\rm {Rep}}_{B_{2},D}(h)$ 的公式，该公式从 ${\rm {Rep}}_{B_{1},D}(h)$ 中计算。
用一个 $V$ 的基和两个 $W$ 的基，重复上一个问题。