在之前的小节中,我们已经用线性映射的加法和标量乘法来表示线性映射,接下来自然要考虑的映射操作是复合。
为了了解复合的表示是如何从两个复合物的表示中产生的,让我们考虑一个例子。
- 示例 2.2
令  和
和  ,固定基
,固定基  ,
, ,
, ,并让这些成为表示。
,并让这些成为表示。

为了表示组合  ,我们固定一个
,我们固定一个  ,表示
,表示  的
的  ,然后表示
,然后表示  的那个。
的那个。  的表示是
的表示是  的矩阵和
的矩阵和  的向量的乘积。
的向量的乘积。

对
在 v {\displaystyle v}  上进行分配和重新分组,得到
上进行分配和重新分组,得到
- = ( ( 1 ⋅ 4 + 1 ⋅ 5 ) v 1 + ( 1 ⋅ 6 + 1 ⋅ 7 ) v 2 + ( 1 ⋅ 8 + 1 ⋅ 9 ) v 3 + ( 1 ⋅ 2 + 1 ⋅ 3 ) v 4 ( 0 ⋅ 4 + 1 ⋅ 5 ) v 1 + ( 0 ⋅ 6 + 1 ⋅ 7 ) v 2 + ( 0 ⋅ 8 + 1 ⋅ 9 ) v 3 + ( 0 ⋅ 2 + 1 ⋅ 3 ) v 4 ( 1 ⋅ 4 + 0 ⋅ 5 ) v 1 + ( 1 ⋅ 6 + 0 ⋅ 7 ) v 2 + ( 1 ⋅ 8 + 0 ⋅ 9 ) v 3 + ( 1 ⋅ 2 + 0 ⋅ 3 ) v 4 ) D {\displaystyle ={\begin{pmatrix}(1\cdot 4+1\cdot 5)v_{1}+(1\cdot 6+1\cdot 7)v_{2}+(1\cdot 8+1\cdot 9)v_{3}+(1\cdot 2+1\cdot 3)v_{4}\\(0\cdot 4+1\cdot 5)v_{1}+(0\cdot 6+1\cdot 7)v_{2}+(0\cdot 8+1\cdot 9)v_{3}+(0\cdot 2+1\cdot 3)v_{4}\\(1\cdot 4+0\cdot 5)v_{1}+(1\cdot 6+0\cdot 7)v_{2}+(1\cdot 8+0\cdot 9)v_{3}+(1\cdot 2+0\cdot 3)v_{4}\end{pmatrix}}_{D}}

我们将其识别为该矩阵-向量积的结果。
- = ( 1 ⋅ 4 + 1 ⋅ 5 1 ⋅ 6 + 1 ⋅ 7 1 ⋅ 8 + 1 ⋅ 9 1 ⋅ 2 + 1 ⋅ 3 0 ⋅ 4 + 1 ⋅ 5 0 ⋅ 6 + 1 ⋅ 7 0 ⋅ 8 + 1 ⋅ 9 0 ⋅ 2 + 1 ⋅ 3 1 ⋅ 4 + 0 ⋅ 5 1 ⋅ 6 + 0 ⋅ 7 1 ⋅ 8 + 0 ⋅ 9 1 ⋅ 2 + 0 ⋅ 3 ) B , D ( v 1 v 2 v 3 v 4 ) D {\displaystyle ={\begin{pmatrix}1\cdot 4+1\cdot 5&1\cdot 6+1\cdot 7&1\cdot 8+1\cdot 9&1\cdot 2+1\cdot 3\\0\cdot 4+1\cdot 5&0\cdot 6+1\cdot 7&0\cdot 8+1\cdot 9&0\cdot 2+1\cdot 3\\1\cdot 4+0\cdot 5&1\cdot 6+0\cdot 7&1\cdot 8+0\cdot 9&1\cdot 2+0\cdot 3\end{pmatrix}}_{B,D}{\begin{pmatrix}v_{1}\\v_{2}\\v_{3}\\v_{4}\end{pmatrix}}_{D}}

因此,表示 g ∘ h {\displaystyle g\circ h}  的矩阵具有 G {\displaystyle G}
的矩阵具有 G {\displaystyle G}  的行与 H {\displaystyle H}
的行与 H {\displaystyle H}  的列组合在一起。
的列组合在一起。
- 定义 2.3
m × r {\displaystyle m\!\times \!r}  矩阵 G {\displaystyle G}
矩阵 G {\displaystyle G}  和 r × n {\displaystyle r\!\times \!n}
和 r × n {\displaystyle r\!\times \!n}  矩阵 H {\displaystyle H}
矩阵 H {\displaystyle H}  的矩阵乘积 是 m × n {\displaystyle m\!\times \!n}
的矩阵乘积 是 m × n {\displaystyle m\!\times \!n}  矩阵 P {\displaystyle P}
矩阵 P {\displaystyle P}  ,其中
,其中
- p i , j = g i , 1 h 1 , j + g i , 2 h 2 , j + ⋯ + g i , r h r , j {\displaystyle p_{i,j}=g_{i,1}h_{1,j}+g_{i,2}h_{2,j}+\dots +g_{i,r}h_{r,j}}

也就是说, i , j {\displaystyle i,j}  -th entry of the product is the dot product of the i {\displaystyle i}
-th entry of the product is the dot product of the i {\displaystyle i}  -th row and the j {\displaystyle j}
-th row and the j {\displaystyle j}  -th column.
-th column.
- G H = ( ⋮ g i , 1 g i , 2 … g i , r ⋮ ) ( h 1 , j … h 2 , j … ⋮ h r , j ) = ( ⋮ … p i , j … ⋮ ) {\displaystyle GH={\begin{pmatrix}&\vdots \\g_{i,1}&g_{i,2}&\ldots &g_{i,r}\\&\vdots \end{pmatrix}}{\begin{pmatrix}&h_{1,j}\\\ldots &h_{2,j}&\ldots \\&\vdots \\&h_{r,j}\end{pmatrix}}={\begin{pmatrix}&\vdots \\\ldots &p_{i,j}&\ldots \\&\vdots \end{pmatrix}}}

- 示例 2.4
来自 示例 2.2 的矩阵以这种方式组合。
- ( 1 ⋅ 4 + 1 ⋅ 5 1 ⋅ 6 + 1 ⋅ 7 1 ⋅ 8 + 1 ⋅ 9 1 ⋅ 2 + 1 ⋅ 3 0 ⋅ 4 + 1 ⋅ 5 0 ⋅ 6 + 1 ⋅ 7 0 ⋅ 8 + 1 ⋅ 9 0 ⋅ 2 + 1 ⋅ 3 1 ⋅ 4 + 0 ⋅ 5 1 ⋅ 6 + 0 ⋅ 7 1 ⋅ 8 + 0 ⋅ 9 1 ⋅ 2 + 0 ⋅ 3 ) = ( 9 13 17 5 5 7 9 3 4 6 8 2 ) {\displaystyle {\begin{pmatrix}1\cdot 4+1\cdot 5&1\cdot 6+1\cdot 7&1\cdot 8+1\cdot 9&1\cdot 2+1\cdot 3\\0\cdot 4+1\cdot 5&0\cdot 6+1\cdot 7&0\cdot 8+1\cdot 9&0\cdot 2+1\cdot 3\\1\cdot 4+0\cdot 5&1\cdot 6+0\cdot 7&1\cdot 8+0\cdot 9&1\cdot 2+0\cdot 3\end{pmatrix}}={\begin{pmatrix}9&13&17&5\\5&7&9&3\\4&6&8&2\end{pmatrix}}}

- 示例 2.5
- ( 2 0 4 6 8 2 ) ( 1 3 5 7 ) = ( 2 ⋅ 1 + 0 ⋅ 5 2 ⋅ 3 + 0 ⋅ 7 4 ⋅ 1 + 6 ⋅ 5 4 ⋅ 3 + 6 ⋅ 7 8 ⋅ 1 + 2 ⋅ 5 8 ⋅ 3 + 2 ⋅ 7 ) = ( 2 6 34 54 18 38 ) {\displaystyle {\begin{pmatrix}2&0\\4&6\\8&2\end{pmatrix}}{\begin{pmatrix}1&3\\5&7\end{pmatrix}}={\begin{pmatrix}2\cdot 1+0\cdot 5&2\cdot 3+0\cdot 7\\4\cdot 1+6\cdot 5&4\cdot 3+6\cdot 7\\8\cdot 1+2\cdot 5&8\cdot 3+2\cdot 7\end{pmatrix}}={\begin{pmatrix}2&6\\34&54\\18&38\end{pmatrix}}}

- 定理 2.6
线性映射的组合由代表的矩阵乘积表示。
- 证明
(该论点与例 2.2类似。) 假设 h : V → W {\displaystyle h:V\to W}  和 g : W → X {\displaystyle g:W\to X}
和 g : W → X {\displaystyle g:W\to X}  分别由 H {\displaystyle H}
分别由 H {\displaystyle H}  和 G {\displaystyle G}
和 G {\displaystyle G}  表示,分别对应基底 B ⊂ V {\displaystyle B\subset V}
表示,分别对应基底 B ⊂ V {\displaystyle B\subset V}  , C ⊂ W {\displaystyle C\subset W}
, C ⊂ W {\displaystyle C\subset W}  和 D ⊂ X {\displaystyle D\subset X}
和 D ⊂ X {\displaystyle D\subset X}  ,大小分别为 n {\displaystyle n}
,大小分别为 n {\displaystyle n}  , r {\displaystyle r}
, r {\displaystyle r}  和 m {\displaystyle m}
和 m {\displaystyle m}  。对于任何 v → ∈ V {\displaystyle {\vec {v}}\in V}
。对于任何 v → ∈ V {\displaystyle {\vec {v}}\in V}  , R e p C ( h ( v → ) ) {\displaystyle {\rm {Rep}}_{C}(\,h({\vec {v}})\,)}
, R e p C ( h ( v → ) ) {\displaystyle {\rm {Rep}}_{C}(\,h({\vec {v}})\,)}  的第 k {\displaystyle k}
的第 k {\displaystyle k}  个分量是
个分量是
- h k , 1 v 1 + ⋯ + h k , n v n {\displaystyle h_{k,1}v_{1}+\cdots +h_{k,n}v_{n}}

因此, R e p D ( g ∘ h ( v → ) ) {\displaystyle {\rm {Rep}}_{D}(\,g\circ h\,({\vec {v}})\,)}  的第 i {\displaystyle i}
的第 i {\displaystyle i}  个分量是:
个分量是:
- g i , 1 ⋅ ( h 1 , 1 v 1 + ⋯ + h 1 , n v n ) + g i , 2 ⋅ ( h 2 , 1 v 1 + ⋯ + h 2 , n v n ) {\displaystyle g_{i,1}\cdot (h_{1,1}v_{1}+\dots +h_{1,n}v_{n})+g_{i,2}\cdot (h_{2,1}v_{1}+\dots +h_{2,n}v_{n})}

- + ⋯ + g i , r ⋅ ( h r , 1 v 1 + ⋯ + h r , n v n ) {\displaystyle +\dots +g_{i,r}\cdot (h_{r,1}v_{1}+\dots +h_{r,n}v_{n})}

将 v {\displaystyle v}  进行分配并重新分组。
进行分配并重新分组。
- = ( g i , 1 h 1 , 1 + g i , 2 h 2 , 1 + ⋯ + g i , r h r , 1 ) ⋅ v 1 {\displaystyle =(g_{i,1}h_{1,1}+g_{i,2}h_{2,1}+\dots +g_{i,r}h_{r,1})\cdot v_{1}}

- + ⋯ + ( g i , 1 h 1 , n + g i , 2 h 2 , n + ⋯ + g i , r h r , n ) ⋅ v n {\displaystyle +\dots +(g_{i,1}h_{1,n}+g_{i,2}h_{2,n}+\dots +g_{i,r}h_{r,n})\cdot v_{n}}

最后,注意到每个 v j {\displaystyle v_{j}}  的系数
的系数
- g i , 1 h 1 , j + g i , 2 h 2 , j + ⋯ + g i , r h r , j {\displaystyle g_{i,1}h_{1,j}+g_{i,2}h_{2,j}+\dots +g_{i,r}h_{r,j}}

与乘积 G H {\displaystyle GH}  中 i , j {\displaystyle i,j}
中 i , j {\displaystyle i,j}  项的定义相符。
项的定义相符。
该定理是支持定义的结果的一个例子。我们可以用这个 **箭头图** 来描绘定义和定理一起表达的内容(“wrt” 代表“相对于”)。
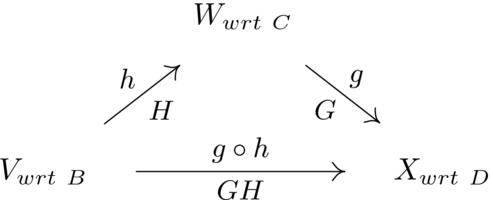
箭头上方,映射表明从 V {\displaystyle V}  到 X {\displaystyle X}
到 X {\displaystyle X}  的两种方式,直接通过合成或通过 W {\displaystyle W}
的两种方式,直接通过合成或通过 W {\displaystyle W}  ,具有相同的效果。
,具有相同的效果。
- v → ⟼ g ∘ h g ( h ( v → ) ) v → ⟼ h h ( v → ) ⟼ g g ( h ( v → ) ) {\displaystyle {\vec {v}}{\stackrel {g\circ h}{\longmapsto }}g(h({\vec {v}}))\qquad {\vec {v}}{\stackrel {h}{\longmapsto }}h({\vec {v}}){\stackrel {g}{\longmapsto }}g(h({\vec {v}}))}

(这仅仅是复合的定义)。箭头下方,矩阵表示产品执行相同的操作——将 G H {\displaystyle GH}  乘以列向量 R e p B ( v → ) {\displaystyle {\rm {Rep}}_{B}({\vec {v}})}
乘以列向量 R e p B ( v → ) {\displaystyle {\rm {Rep}}_{B}({\vec {v}})}  与首先将列向量乘以 H {\displaystyle H}
与首先将列向量乘以 H {\displaystyle H}  ,然后将结果乘以 G {\displaystyle G}
,然后将结果乘以 G {\displaystyle G}  具有相同的效果。
具有相同的效果。
- R e p B , D ( g ∘ h ) = G H = R e p C , D ( g ) R e p B , C ( h ) {\displaystyle {\rm {Rep}}_{B,D}(g\circ h)=GH={\rm {Rep}}_{C,D}(g)\,{\rm {Rep}}_{B,C}(h)}

矩阵乘法运算的定义并没有限制我们将其视为线性映射复合的表示。我们可以通过将其作为一种机械程序进行研究来深入了解这种操作。令人惊奇的是,行和列是如何结合的。
这种结合的一个方面是所涉及矩阵的大小非常重要。简单来说, m × r times r × n equals m × n {\displaystyle m\!\times \!r{\text{ times }}r\!\times \!n{\text{ equals }}m\!\times \!n}  .
.
- 示例 2.7
这个乘法没有定义
- ( − 1 2 0 0 10 1.1 ) ( 0 0 0 2 ) {\displaystyle {\begin{pmatrix}-1&2&0\\0&10&1.1\end{pmatrix}}{\begin{pmatrix}0&0\\0&2\end{pmatrix}}}

因为左侧的列数不等于右侧的行数。
就底层映射而言,大小必须匹配这一事实反映了矩阵乘法仅在相应的函数复合
- dimension n space ⟶ h dimension r space ⟶ g dimension m space {\displaystyle {\text{dimension }}n{\text{ space}}\;{\stackrel {h}{\longrightarrow }}\;{\text{dimension }}r{\text{ space}}\;{\stackrel {g}{\longrightarrow }}\;{\text{dimension }}m{\text{ space}}}

是可能的。
矩阵乘法运算中行和列组合方式的另一个方面是,在 i , j {\displaystyle i,j}  项的定义中
项的定义中
- p i , j = g i , 1 h 1 , j + g i , 2 h 2 , j + ⋯ + g i , r h r , j {\displaystyle p_{i,j}=g_{i,{\color {red}1}}h_{{\color {red}1},j}+g_{i,{\color {red}2}}h_{{\color {red}2},j}+\dots +g_{i,{\color {red}r}}h_{{\color {red}r},j}}

g {\displaystyle g}  上的红色下标是列指示符,而 h {\displaystyle h}
上的红色下标是列指示符,而 h {\displaystyle h}  上的红色下标表示行。也就是说,求和是在 G {\displaystyle G}
上的红色下标表示行。也就是说,求和是在 G {\displaystyle G}  的列上进行,但在 H {\displaystyle H}
的列上进行,但在 H {\displaystyle H}  的行上进行;左侧的处理方式与右侧不同,因此 G H {\displaystyle GH}
的行上进行;左侧的处理方式与右侧不同,因此 G H {\displaystyle GH}  可能不等于 H G {\displaystyle HG}
可能不等于 H G {\displaystyle HG}  。矩阵乘法不满足交换律。
。矩阵乘法不满足交换律。
- 示例 2.9
矩阵乘法几乎从不满足交换律。通过以两种方式相乘随机选择的矩阵来测试这一点。
- ( 1 2 3 4 ) ( 5 6 7 8 ) = ( 19 22 43 50 ) ( 5 6 7 8 ) ( 1 2 3 4 ) = ( 23 34 31 46 ) {\displaystyle {\begin{pmatrix}1&2\\3&4\end{pmatrix}}{\begin{pmatrix}5&6\\7&8\end{pmatrix}}={\begin{pmatrix}19&22\\43&50\end{pmatrix}}\qquad {\begin{pmatrix}5&6\\7&8\end{pmatrix}}{\begin{pmatrix}1&2\\3&4\end{pmatrix}}={\begin{pmatrix}23&34\\31&46\end{pmatrix}}}

- 示例 2.10
交换律失效的情况可能更加严重
- ( 5 6 7 8 ) ( 1 2 0 3 4 0 ) = ( 23 34 0 31 46 0 ) {\displaystyle {\begin{pmatrix}5&6\\7&8\end{pmatrix}}{\begin{pmatrix}1&2&0\\3&4&0\end{pmatrix}}={\begin{pmatrix}23&34&0\\31&46&0\end{pmatrix}}}

然而
- ( 1 2 0 3 4 0 ) ( 5 6 7 8 ) {\displaystyle {\begin{pmatrix}1&2&0\\3&4&0\end{pmatrix}}{\begin{pmatrix}5&6\\7&8\end{pmatrix}}}

甚至都没有定义。
除了不满足交换律外,矩阵乘法在代数上表现良好。以下是一些不错的性质,更多性质可以在 习题 10 和 习题 11 中找到。
- 注 2.13
我们也可以通过繁琐的索引运算来证明这个结果。例如,结合律可以写成: ( F G ) H {\displaystyle (FG)H}  的第 i , j {\displaystyle i,j}
的第 i , j {\displaystyle i,j}  个元素是
个元素是
- ( f i , 1 g 1 , 1 + f i , 2 g 2 , 1 + ⋯ + f i , r g r , 1 ) h 1 , j + ( f i , 1 g 1 , 2 + f i , 2 g 2 , 2 + ⋯ + f i , r g r , 2 ) h 2 , j ⋮ + ( f i , 1 g 1 , s + f i , 2 g 2 , s + ⋯ + f i , r g r , s ) h s , j {\displaystyle {\begin{array}{rl}&(f_{i,1}g_{1,1}+f_{i,2}g_{2,1}+\dots +f_{i,r}g_{r,1})h_{1,j}\\&\quad +(f_{i,1}g_{1,2}+f_{i,2}g_{2,2}+\dots +f_{i,r}g_{r,2})h_{2,j}\\&\quad \;\;\vdots \\&\quad +(f_{i,1}g_{1,s}+f_{i,2}g_{2,s}+\dots +f_{i,r}g_{r,s})h_{s,j}\end{array}}}

(其中 F {\displaystyle F}  , G {\displaystyle G}
, G {\displaystyle G}  和 H {\displaystyle H}
和 H {\displaystyle H}  是 m × r {\displaystyle m\!\times \!r}
是 m × r {\displaystyle m\!\times \!r}  , r × s {\displaystyle r\!\times \!s}
, r × s {\displaystyle r\!\times \!s}  和 s × n {\displaystyle s\!\times \!n}
和 s × n {\displaystyle s\!\times \!n}  矩阵),分配
矩阵),分配
- f i , 1 g 1 , 1 h 1 , j + f i , 2 g 2 , 1 h 1 , j + ⋯ + f i , r g r , 1 h 1 , j + f i , 1 g 1 , 2 h 2 , j + f i , 2 g 2 , 2 h 2 , j + ⋯ + f i , r g r , 2 h 2 , j ⋮ + f i , 1 g 1 , s h s , j + f i , 2 g 2 , s h s , j + ⋯ + f i , r g r , s h s , j {\displaystyle {\begin{array}{rl}&f_{i,1}g_{1,1}h_{1,j}+f_{i,2}g_{2,1}h_{1,j}+\dots +f_{i,r}g_{r,1}h_{1,j}\\&\quad +f_{i,1}g_{1,2}h_{2,j}+f_{i,2}g_{2,2}h_{2,j}+\dots +f_{i,r}g_{r,2}h_{2,j}\\&\quad \;\;\vdots \\&\quad +f_{i,1}g_{1,s}h_{s,j}+f_{i,2}g_{2,s}h_{s,j}+\dots +f_{i,r}g_{r,s}h_{s,j}\end{array}}}

并围绕 f {\displaystyle f}  进行重新分组
进行重新分组
- f i , 1 ( g 1 , 1 h 1 , j + g 1 , 2 h 2 , j + ⋯ + g 1 , s h s , j ) + f i , 2 ( g 2 , 1 h 1 , j + g 2 , 2 h 2 , j + ⋯ + g 2 , s h s , j ) ⋮ + f i , r ( g r , 1 h 1 , j + g r , 2 h 2 , j + ⋯ + g r , s h s , j ) {\displaystyle {\begin{array}{rl}&f_{i,1}(g_{1,1}h_{1,j}+g_{1,2}h_{2,j}+\dots +g_{1,s}h_{s,j})\\&\quad +f_{i,2}(g_{2,1}h_{1,j}+g_{2,2}h_{2,j}+\dots +g_{2,s}h_{s,j})\\&\quad \;\;\vdots \\&\quad +f_{i,r}(g_{r,1}h_{1,j}+g_{r,2}h_{2,j}+\dots +g_{r,s}h_{s,j})\end{array}}}

以获得 i , j {\displaystyle i,j}  的 F ( G H ) {\displaystyle F(GH)}
的 F ( G H ) {\displaystyle F(GH)}  项。
项。
对比验证结合律的两种方法,一种是在证明中,另一种是在上面。上面的论证很难理解,因为虽然计算很容易检查,但算术似乎与任何想法都没有联系(它也基本上重复了 定理 2.6 的证明,因此效率低下)。证明中的论证更短、更清晰,并说明了这种性质“真正”成立的原因。这说明了在向量空间章节前言中提到的评论——至少在某些情况下,来自更高层次结构的论证更清晰。
我们现在已经了解了如何从两个线性映射的表示中推导出它们组合的表示。我们称这个组合为两个矩阵的乘积。这种运算极其重要。在我们继续研究如何表示线性映射的逆之前,我们将在下一小节中进一步探讨它。
- 本练习建议所有读者完成。
- 本练习建议所有读者完成。
- 本练习建议所有读者完成。
- 本练习建议所有读者完成。
- 问题 5
找到从以下开始得到的方程组
- h 1 , 1 x 1 + h 1 , 2 x 2 + h 1 , 3 x 3 = d 1 h 2 , 1 x 1 + h 2 , 2 x 2 + h 2 , 3 x 3 = d 2 {\displaystyle {\begin{array}{*{3}{rc}r}h_{1,1}x_{1}&+&h_{1,2}x_{2}&+&h_{1,3}x_{3}&=&d_{1}\\h_{2,1}x_{1}&+&h_{2,2}x_{2}&+&h_{2,3}x_{3}&=&d_{2}\end{array}}}

并进行此变量更改(即替换)。
- x 1 = g 1 , 1 y 1 + g 1 , 2 y 2 x 2 = g 2 , 1 y 1 + g 2 , 2 y 2 x 3 = g 3 , 1 y 1 + g 3 , 2 y 2 {\displaystyle {\begin{array}{*{2}{rc}r}x_{1}&=&g_{1,1}y_{1}&+&g_{1,2}y_{2}\\x_{2}&=&g_{2,1}y_{1}&+&g_{2,2}y_{2}\\x_{3}&=&g_{3,1}y_{1}&+&g_{3,2}y_{2}\end{array}}}

- 问题 6
正如定义 2.3 指出,矩阵乘法运算概括了点积。一个 1 × n {\displaystyle 1\!\times \!n}  行向量和一个 n × 1 {\displaystyle n\!\times \!1}
行向量和一个 n × 1 {\displaystyle n\!\times \!1}  列向量的点积是否与其矩阵乘积相同?
列向量的点积是否与其矩阵乘积相同?
- 本练习建议所有读者完成。
- 问题 8
证明在 R 1 {\displaystyle \mathbb {R} ^{1}}  上的线性变换的复合运算满足交换律。这对于任何一维空间都成立吗?
上的线性变换的复合运算满足交换律。这对于任何一维空间都成立吗?
- 问题 9
为什么矩阵乘法不定义为逐元素乘法?这样会更容易,而且也满足交换律。
- 本练习建议所有读者完成。
- 问题 10
- 证明 H p H q = H p + q {\displaystyle H^{p}H^{q}=H^{p+q}}
 且 ( H p ) q = H p q {\displaystyle (H^{p})^{q}=H^{pq}}
且 ( H p ) q = H p q {\displaystyle (H^{p})^{q}=H^{pq}}  对于正整数 p , q {\displaystyle p,q}
对于正整数 p , q {\displaystyle p,q}  成立。
成立。 - 证明 ( r H ) p = r p ⋅ H p {\displaystyle (rH)^{p}=r^{p}\cdot H^{p}}
 对于任何正整数 p {\displaystyle p}
对于任何正整数 p {\displaystyle p}  和标量 r ∈ R {\displaystyle r\in \mathbb {R} }
和标量 r ∈ R {\displaystyle r\in \mathbb {R} }  成立。
成立。
- 本练习建议所有读者完成。
- 问题 11
- 矩阵乘法如何与标量乘法交互: r ( G H ) = ( r G ) H {\displaystyle r(GH)=(rG)H}
 吗? G ( r H ) = r ( G H ) {\displaystyle G(rH)=r(GH)}
吗? G ( r H ) = r ( G H ) {\displaystyle G(rH)=r(GH)}  吗?
吗? - 矩阵乘法如何与线性组合交互: F ( r G + s H ) = r ( F G ) + s ( F H ) {\displaystyle F(rG+sH)=r(FG)+s(FH)}
 吗? ( r F + s G ) H = r F H + s G H {\displaystyle (rF+sG)H=rFH+sGH}
吗? ( r F + s G ) H = r F H + s G H {\displaystyle (rF+sG)H=rFH+sGH}  吗?
吗?
- 本练习建议所有读者完成。
- 问题 13
在 R 3 {\displaystyle \mathbb {R} ^{3}}  中绕某个轴旋转向量是一个线性映射。证明线性映射不满足交换律,方法是几何地证明旋转不满足交换律。
中绕某个轴旋转向量是一个线性映射。证明线性映射不满足交换律,方法是几何地证明旋转不满足交换律。
- 问题 14
在 定理 2.12 的证明中,使用了一些映射。这些映射的定义域和值域是什么?
- 问题 15
矩阵秩如何与矩阵乘法交互?
- 两个秩为 n {\displaystyle n}
 的矩阵的乘积的秩可以小于 n {\displaystyle n}
的矩阵的乘积的秩可以小于 n {\displaystyle n}  吗?可以大于吗?
吗?可以大于吗? - 证明两个矩阵的乘积的秩小于等于每个因子的秩的最小值。
- 问题 16
“与…交换”在 n × n {\displaystyle n\!\times \!n}  矩阵中是等价关系吗?
矩阵中是等价关系吗?
- 本练习建议所有读者完成。
- 问题 18
证明,对于方阵, ( S + T ) ( S − T ) {\displaystyle (S+T)(S-T)}  不一定等于 S 2 − T 2 {\displaystyle S^{2}-T^{2}}
不一定等于 S 2 − T 2 {\displaystyle S^{2}-T^{2}}  。
。
- 本练习建议所有读者完成。
- 问题 21
- 证明对于任何 2 × 2 {\displaystyle 2\!\times \!2}
 矩阵 T {\displaystyle T}
矩阵 T {\displaystyle T}  ,存在标量 c 0 , … , c 4 {\displaystyle c_{0},\dots ,c_{4}}
,存在标量 c 0 , … , c 4 {\displaystyle c_{0},\dots ,c_{4}}  且不全为 0 {\displaystyle 0}
且不全为 0 {\displaystyle 0}  ,使得组合 c 4 T 4 + c 3 T 3 + c 2 T 2 + c 1 T + c 0 I {\displaystyle c_{4}T^{4}+c_{3}T^{3}+c_{2}T^{2}+c_{1}T+c_{0}I}
,使得组合 c 4 T 4 + c 3 T 3 + c 2 T 2 + c 1 T + c 0 I {\displaystyle c_{4}T^{4}+c_{3}T^{3}+c_{2}T^{2}+c_{1}T+c_{0}I}  为零矩阵(其中 I {\displaystyle I}
为零矩阵(其中 I {\displaystyle I}  是 2 × 2 {\displaystyle 2\!\times \!2}
是 2 × 2 {\displaystyle 2\!\times \!2}  单位矩阵,其 1 , 1 {\displaystyle 1,1}
单位矩阵,其 1 , 1 {\displaystyle 1,1}  和 2 , 2 {\displaystyle 2,2}
和 2 , 2 {\displaystyle 2,2}  元素为 1 {\displaystyle 1}
元素为 1 {\displaystyle 1}  ,其余元素为零;参见 习题 19)。
,其余元素为零;参见 习题 19)。 - 令 p ( x ) {\displaystyle p(x)}
 是一个多项式 p ( x ) = c n x n + ⋯ + c 1 x + c 0 {\displaystyle p(x)=c_{n}x^{n}+\dots +c_{1}x+c_{0}}
是一个多项式 p ( x ) = c n x n + ⋯ + c 1 x + c 0 {\displaystyle p(x)=c_{n}x^{n}+\dots +c_{1}x+c_{0}}  。如果 T {\displaystyle T}
。如果 T {\displaystyle T}  是方阵,则定义 p ( T ) {\displaystyle p(T)}
是方阵,则定义 p ( T ) {\displaystyle p(T)}  为矩阵 c n T n + ⋯ + c 1 T + I {\displaystyle c_{n}T^{n}+\dots +c_{1}T+I}
为矩阵 c n T n + ⋯ + c 1 T + I {\displaystyle c_{n}T^{n}+\dots +c_{1}T+I}  (其中 I {\displaystyle I}
(其中 I {\displaystyle I}  是适当大小的单位矩阵)。证明对于任何方阵,都存在一个多项式,使得 p ( T ) {\displaystyle p(T)}
是适当大小的单位矩阵)。证明对于任何方阵,都存在一个多项式,使得 p ( T ) {\displaystyle p(T)}  为零矩阵。
为零矩阵。 - 方阵的最小多项式 m ( x ) {\displaystyle m(x)}
 是使得 m ( T ) {\displaystyle m(T)}
是使得 m ( T ) {\displaystyle m(T)}  为零矩阵的,最低次且首项系数为 1 {\displaystyle 1}
为零矩阵的,最低次且首项系数为 1 {\displaystyle 1}  的多项式。求此矩阵的最小多项式。
的多项式。求此矩阵的最小多项式。- ( 3 / 2 − 1 / 2 1 / 2 3 / 2 ) {\displaystyle {\begin{pmatrix}{\sqrt {3}}/2&-1/2\\1/2&{\sqrt {3}}/2\end{pmatrix}}}

(这是关于 E 2 , E 2 {\displaystyle {\mathcal {E}}_{2},{\mathcal {E}}_{2}}  ,标准基,关于 π / 6 {\displaystyle \pi /6}
,标准基,关于 π / 6 {\displaystyle \pi /6}  弧度的逆时针旋转的表示。)
弧度的逆时针旋转的表示。)
- 问题 23
回想一下 a 1 , a 2 , … , a n {\displaystyle a_{1},a_{2},\dots ,a_{n}}  数字序列的求和符号。
数字序列的求和符号。
- ∑ i = 1 n a i = a 1 + a 2 + ⋯ + a n {\displaystyle \sum _{i=1}^{n}a_{i}=a_{1}+a_{2}+\dots +a_{n}}

在这个符号中, i , j {\displaystyle i,j}  是 G {\displaystyle G}
是 G {\displaystyle G}  和 H {\displaystyle H}
和 H {\displaystyle H}  乘积的项是这个。
乘积的项是这个。
- p i , j = ∑ k = 1 r g i , k h k , j {\displaystyle p_{i,j}=\sum _{k=1}^{r}g_{i,k}h_{k,j}}

使用此符号,
- 重新证明矩阵乘法满足结合律;
- 重新证明 定理 2.6。
解答








































































































































































