线性代数/主题：晶体

每个人都注意到食盐是立方体形状的。

值得注意的是，对立方体外形的解释是最简单的：内部形状，即原子的排列方式，也是立方体形状的。内部结构如下图所示。食盐是氯化钠，图中显示的小球是钠，大球是氯。（为了简化视图，只显示了前、上、右边的钠和氯。）

当我们将少量食盐散布在桌面上时，我们看到的食盐颗粒由许多重复的这种基本单元组成。也就是说，这些原子立方体堆叠起来，形成了我们看到的更大的立方体结构。像食盐这样的具有规则内部结构的固体被称为晶体。

我们可以将注意力集中在正面上。在那里，我们看到这种模式重复了很多次。

该单元格角之间的距离约为 3.34 埃（1 埃为$10^{-10}$ 米）。显然，这个单位不适合描述晶格中的点。相反，我们自然地采用这种基底作为单位。

$\langle {\begin{pmatrix}3.34\\0\end{pmatrix}},{\begin{pmatrix}0\\3.34\end{pmatrix}}\rangle$

然后我们可以描述，例如，上面图片中右上角的角为$3{\vec {\beta }}_{1}+2{\vec {\beta }}_{2}$.

另一个常见的晶体是铅笔芯。它是石墨，由以这种形状排列的碳原子构成。

这是一层石墨。一块石墨由许多层这种平面堆叠而成。（平面之间的化学键比平面内部的键弱得多，这解释了为什么石墨可以书写——它可以被剪切，使得平面滑落并留在纸上。）可以通过将六边形环分解成三个区域来形成一个方便的长度单位，这三个区域是这个晶胞的旋转。

        

那么，一个自然基底将由形成该晶胞边的向量组成。底部和斜面的距离是$1.42$ 埃，所以这个

$\langle {\begin{pmatrix}1.42\\0\end{pmatrix}},{\begin{pmatrix}1.23\\.71\end{pmatrix}}\rangle$

是一个好的基底。

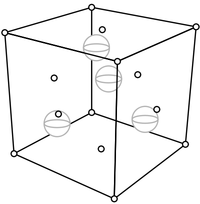
方便基底的选择可以扩展到三维空间。另一种由碳形成的常见晶体是金刚石。与食盐一样，它也是由立方体构成，但每个立方体内的结构比食盐的复杂。除了每个角都有一个碳原子外，

每个面的中间也有一个碳原子。

（为了清楚地显示添加的面碳原子，角碳原子已缩减为点。）立方体内部还有四个碳原子，两个位于底部向上四分之一处，另外两个位于顶部向下四分之一处。

（与以前一样，此处先前显示的碳原子已缩减为点。）立方体沿任何边的距离为$2.18$ 埃。因此，描述碳原子位置及其之间键的自然基底是这个。

$\langle {\begin{pmatrix}2.18\\0\\0\end{pmatrix}},{\begin{pmatrix}0\\2.18\\0\end{pmatrix}},{\begin{pmatrix}0\\0\\2.18\end{pmatrix}}\rangle$

即使这里给出的几个例子也表明，晶体的结构非常复杂，需要一个有组织的系统来给出原子的位置以及它们是如何化学键合的。用于组织的工具之一是一个方便的基底。这种基底的应用很简单，但它显示了一个基底概念自然产生的环境。本章的工作只是将这个简单的概念发展起来。

练习

问题 1

一小块食盐的一面有多少个基本区域？ (用尺子可以估计该面是一个边长为 $0.1$ 厘米的正方形。)

问题 2

在石墨的图片中，想象我们对一个点 $5.67$ 埃向上和 $3.14$ 埃从原点出发感兴趣。

1. 用石墨给出的基底来表示该点。
2. 该点距离原点多少个六边形形状？
3. 用第二个基底表示该点，其中第一个基底向量相同，但第二个基底向量与第一个基底向量垂直（向上穿过平面），长度相同。

问题 3

给出金刚石立方体中原子在基底和埃中的位置。

问题 4

这说明了如何根据物质的晶体形状计算出晶胞的尺寸（参见 Ebbing 1993, p. 462）。

1. 回想一下，一摩尔中有 $6.022\times 10^{23}$ 个原子（这是阿伏伽德罗常数）。从这一点出发，以及铂的质量为 $195.08$ 克每摩尔，计算每个原子的质量。
2. 铂在面心立方晶格中结晶，每个晶格点上都有原子，也就是说，它看起来像上面给出的金刚石晶体的中间图片。找到每个晶胞中的铂原子数（提示：将位于单个晶胞内的铂原子分数加起来）。
3. 据此，找出晶胞的质量。
4. 铂晶体的密度为 $21.45$ 克每立方厘米。据此，以及晶胞的质量，计算出晶胞的体积。
5. 找出每条边的长度。
6. 描述一个自然的三维基底。

解决方案

参考资料

• Ebbing, Darrell D. (1993), General Chemistry (Fourth ed.), Houghton Mifflin.