"高维几何"听起来很奇特。它确实很奇特——有趣且令人大开眼界。但它并不遥不可及。
我们首先定义一维空间为集合  。为了看到这个定义是合理的,绘制一个一维空间
。为了看到这个定义是合理的,绘制一个一维空间

并进行与  的通常对应:选择一个点标记为
的通常对应:选择一个点标记为  ,另一个标记为
,另一个标记为  。
。

现在,有了刻度和方向,找到对应于例如  的点很容易——从
的点很容易——从  开始,沿着
开始,沿着  的方向(即正方向)前进,但不要停在那里,继续前进
的方向(即正方向)前进,但不要停在那里,继续前进  倍的距离。
倍的距离。
这里的基本思想是将大小与方向结合起来,这是扩展到更高维度的关键。
由大小和方向组成的对象称为向量(我们将使用与上一节相同的词,因为我们将在下面展示如何用列向量描述这样的对象)。我们可以将向量绘制为具有特定长度并指向某个方向。

这里有一个微妙之处——这些向量

是相等的,即使它们起始位置不同,因为它们具有相等的长度和相等的方向。再说一次:这些向量不仅仅是相似,它们是相等的。
如何理解在不同位置的事物可以相等?将向量视为表示位移("向量"在拉丁语中意为 "载体" 或 "旅行者")。这些正方形经历了相同的位移,尽管这些位移起始位置不同。

有时,为了强调向量不固定的特性,它们被称为自由向量。因此,这些自由向量是相等的,因为每个向量都表示一个向右移动一个单位,向上移动两个单位的位移。
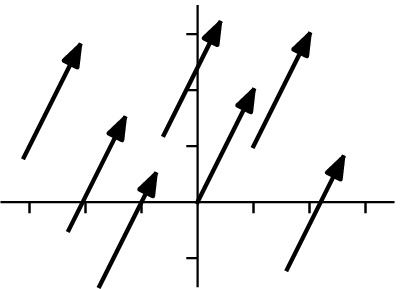
更一般地,平面上向量相等,当且仅当它们在第一分量上的变化相同,在第二分量上的变化也相同:从  指向
指向  的向量等于从
的向量等于从  指向
指向  的向量,当且仅当
的向量,当且仅当  且
且  。
。
像“从  开始的向量,如果它要延伸到
开始的向量,如果它要延伸到  ” 这样的表达很笨拙。相反,我们将这样的向量描述为
” 这样的表达很笨拙。相反,我们将这样的向量描述为

例如,上面显示的“向右移动一个单位,向上移动两个单位”的箭头就描绘了这个向量。

我们通常将箭头绘制为从原点开始,并称其为规范位置(或自然位置)。当向量

处于其规范位置时,它延伸到端点  .
.
我们通常只提及“点
 "
"
”,而不是“该向量的规范位置的端点”。
因此,我们将这两个集合都称为  .
.

在上一节中,我们用代数的动机定义了向量和向量运算;

现在我们可以从几何角度来解释这些运算。例如,如果 代表一个位移,那么
代表一个位移,那么 代表一个方向相同但距离是其三倍的位移,而
代表一个方向相同但距离是其三倍的位移,而  代表一个与
代表一个与  相同距离但在相反方向的位移。
相同距离但在相反方向的位移。

并且,当  和
和  代表位移时,
代表位移时, 代表这两个位移的组合。
代表这两个位移的组合。
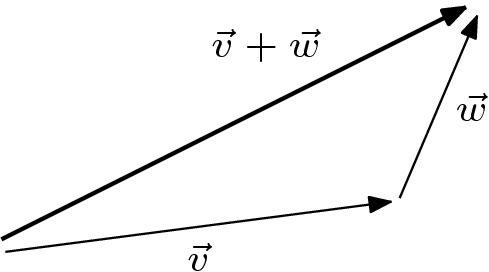
这条长箭头表示这种意义上的组合位移:如果在一分钟内,一艘船相对于地球的运动使它产生了  的位移,而一名乘客相对于船的甲板的运动产生了
的位移,而一名乘客相对于船的甲板的运动产生了  的位移,那么
的位移,那么  就是乘客相对于地球的位移。
就是乘客相对于地球的位移。
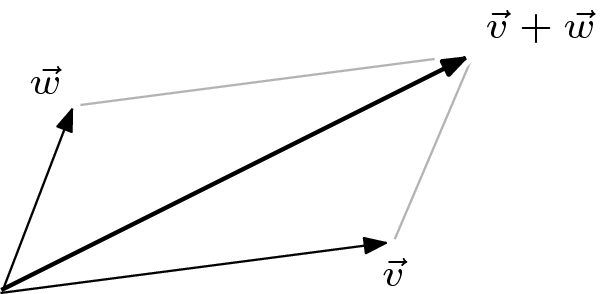
理解向量和的另一种方法是使用平行四边形法则。画出由向量  形成的平行四边形,那么和
形成的平行四边形,那么和  沿着对角线延伸到远角。
沿着对角线延伸到远角。
以上图示展示了向量和向量运算在  中的行为。我们可以将这种行为扩展到
中的行为。我们可以将这种行为扩展到  ,甚至扩展到我们没有图像的更高维空间,并进行明显的推广:如果一个自由向量从
,甚至扩展到我们没有图像的更高维空间,并进行明显的推广:如果一个自由向量从  开始,在
开始,在  结束,那么它可以用下面这列向量表示
结束,那么它可以用下面这列向量表示

(向量相等如果它们有相同的表示),我们并不太在意区分一个点和以该点为终点的向量的规范表示,

加法和标量乘法都是按分量进行的。
我们已经考虑了点,现在转向直线。
在  中,经过
中,经过  和
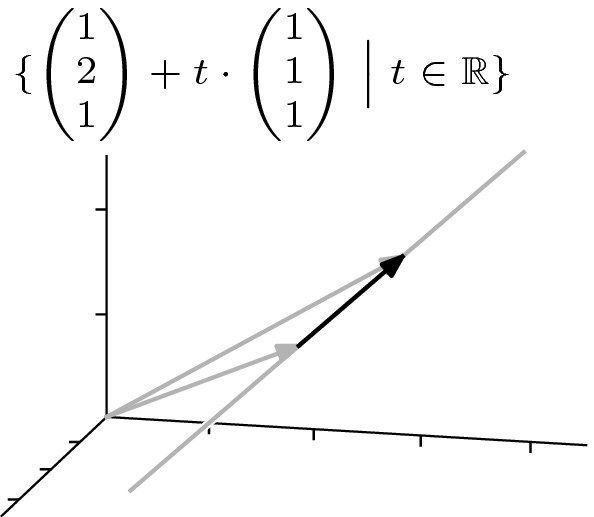
和  的直线包含(以下集合中向量的终点)
的直线包含(以下集合中向量的终点)

该描述表达了这幅图。
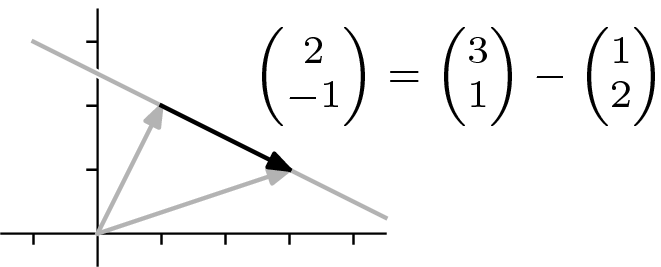
与参数  相关的向量在其整个主体都在直线上——它是一个方向向量,用于直线。请注意,直线上位于
相关的向量在其整个主体都在直线上——它是一个方向向量,用于直线。请注意,直线上位于  左侧的点使用
左侧的点使用  的负值来描述。
的负值来描述。
在  中,经过
中,经过  和
和  的直线是以下形式的向量集(向量终点)
的直线是以下形式的向量集(向量终点)
更高维空间中的直线也是以相同的方式工作的。
如果一条直线使用一个参数,因此可以在一个维度上自由移动,那么一个平面必须包含两个参数。例如,经过点  ,
, ,和
,和  的平面包含(以下集合中向量的终点)
的平面包含(以下集合中向量的终点)

(与参数相关的列向量

是两个整个向量都在平面上的向量)。与直线一样,请注意,这个平面中的某些点是用负数描述的  或负数
或负数  或两者。
或两者。
在代数和微积分中经常遇到的平面描述使用单个方程作为描述平面中点的一、二、三坐标之间关系的条件。

从这种描述到我们在这本书中喜欢的向量描述的转换是将条件视为一个方程线性系统,并将  参数化。
参数化。

从直线和平面的推广,我们定义一个 维线性曲面(或
维线性曲面(或 平面)在
平面)在  中为
中为  ,其中
,其中  。例如,在
。例如,在  中,
中,

是一条直线,

是一个平面,以及

是一个三维线性曲面。同样,直观的理解是,直线允许在一个方向上运动,平面允许在两个方向的组合上运动,等等。
线性曲面的描述可能会对维度产生误导 - 这个

是一个退化的平面,因为它实际上是一条直线。

我们将在第二章的线性无关部分看到,向量之间的哪些关系会导致它们生成的线性曲面退化。
在本节的最后,我们将用几何术语重新说明第一节的结论。首先,具有  个未知数的线性方程组的解集是
个未知数的线性方程组的解集是  中的线性曲面。具体来说,它是一个
中的线性曲面。具体来说,它是一个  维线性曲面,其中
维线性曲面,其中  是系统梯形形式中自由变量的个数。其次,齐次线性方程组的解集是经过原点的线性曲面。最后,我们可以将任何线性方程组的通解集看作是其关联齐次方程组的解集从原点偏移一个向量,即任何特解。
是系统梯形形式中自由变量的个数。其次,齐次线性方程组的解集是经过原点的线性曲面。最后,我们可以将任何线性方程组的通解集看作是其关联齐次方程组的解集从原点偏移一个向量,即任何特解。
- 此练习推荐所有读者尝试。
- 问题 1
找到每个向量的规范名称。
- 从
 到
到  的向量,在
的向量,在  中。
中。 - 从
 到
到  的向量,在
的向量,在  中。
中。 - 从
 到
到  的向量,在
的向量,在  中。
中。 - 从
 到
到  的向量,在
的向量,在  中。
中。
- 此练习推荐所有读者尝试。
- 问题 2
判断这两个向量是否相等。
- 从
 到
到  的向量,和从
的向量,和从  到
到  的向量。
的向量。 - 从
 到
到  的向量,和从
的向量,和从  到
到  的向量。
的向量。
- 此练习推荐所有读者尝试。
- 问题 3
向量  是否位于通过
是否位于通过  和
和  的直线上?
的直线上?
- 此练习推荐所有读者尝试。
- 问题 4
- 描述通过
 ,
,  , 和
, 和  的平面。
的平面。 - 原点在这个平面上吗?
- 问题 5
描述包含以下点和直线的平面。

- 此练习推荐所有读者尝试。
- 问题 6
找到这些平面的交点

- 此练习推荐所有读者尝试。
- 问题 7
如果可能,求解以下各对的交集。
-


-


- 问题 8
当一个平面不经过原点时,对位于平面内的向量的操作比平面经过原点时要复杂。请考虑本节中关于平面

以及它显示的三个向量,其端点为  ,
,  , 以及
, 以及  .
.
- 重新绘制图像,包括在平面内长度是具有终点
 的向量的两倍的向量。你的向量的终点不是
的向量的两倍的向量。你的向量的终点不是  ; 它是多少?
; 它是多少? - 重新绘制图像,包括在平面内显示以
 和
和  为终点的向量的和的平行四边形。和的终点,在对角线上,不是
为终点的向量的和的平行四边形。和的终点,在对角线上,不是  ; 它是多少?
; 它是多少?
- 问题 10
应该如何定义  ?
?
- 此练习推荐所有读者尝试。
- ?问题 11
一个人以  英里/小时的速度向东行驶,发现风似乎直接从北方吹来。当他的速度翻倍时,风似乎从东北方向吹来。风的速率是多少?(Klamkin 1957)
英里/小时的速度向东行驶,发现风似乎直接从北方吹来。当他的速度翻倍时,风似乎从东北方向吹来。风的速率是多少?(Klamkin 1957)
- 此练习推荐所有读者尝试。
- 问题 12
欧几里得将平面描述为“一个与直线在自身上平行的表面”。注释者(例如,希罗)将此解释为“(平面表面)是这样的,如果一条直线经过它的两个点,这条直线在各个位置都与它完全重合,所有方向都是这样”。(来自 Heath 1956 的翻译,第 171-172 页。)本节中描述的平面具有该特性吗?这个描述是否充分定义了平面?
解答
- Klamkin, M. S. (proposer) (1957), "Trickie T-27", Mathematics Magazine, 30 (3): 173 .
- Heath, T. (1956), Euclid's Elements, vol. 1, Dover.











































































































