实分析/连续性

←极限

实分析 连续性

总变差→

现在我们已经定义了函数的极限，我们可以定义一个函数连续意味着什么。连续性的概念抓住了函数“没有突然跳跃或振荡”的直观图像。然而，在本页中，我们将从这个基本定义转向具有清单的内容；具有严谨性的内容。这不仅在实分析中很重要，在其他数学领域也很重要。

连续性标志着函数分类的新方法，特别是当本页后面解释的定理被使用时，这种分类尤为突出。然而，如果读者是线性地阅读本维基教科书，那么应该注意，本维基教科书将描述具有比连续性更多属性的函数。例如，初等数学中的函数，如多项式、三角函数以及指数和对数函数，包含比连续函数更多级别的属性。我们还将看到一些不连续函数的例子，以提供一些关于不符合条件的常见函数的说明。

定义

I 上的连续函数定义

---

给定一个区间 $I$ 和一个函数 $f:I\to \mathbb {R}$，在I 上连续被定义为遵循以下性质

$\forall \varepsilon >0:\exists \delta >0:\forall x\in I:\exists c\in \mathbb {R} :|x-c|<\delta \implies |f(x)-f(c)|<\varepsilon$

它表示为 $\lim _{x\to c}f(x)=f(c)$

读者可能会注意到这个定义与极限的定义之间的相似之处，因为与极限不同，在极限中，函数 $f$ 可以收敛到任何值，连续性限制返回值只能是函数 $f$ 被评估时预期的值。这种额外的限制提供了许多新的定理，如下面的标题所示，其中一些最重要的定理将被展示。

运算

由于极限在代数运算下保持不变，让我们检查一下连续性是否也是如此。

代数运算

我们看到，如果 $f(x)$ 和 $g(x)$ 在 c 处都连续，连续性在以下情况下仍然有效

在代数运算下保持不变的连续函数列表

加法	$\lim _{x\rightarrow c}{(f+g)(x)}=f(c)+g(c)$
减法	$\lim _{x\rightarrow c}{(f-g)(x)}=f(c)-g(c)$
乘积	$\lim _{x\rightarrow c}{(f\cdot g)(x)}=f(c)\cdot g(c)$
函数的倍数	$\lim _{x\rightarrow c}{\lambda \cdot g(x)}=\lambda \cdot g(c)$
倒数	$\lim _{x\rightarrow c}{\left({\dfrac {1}{g}}\right)(x)}={\dfrac {1}{g(c)}}$
除法	$\lim _{x\rightarrow c}{\left({\dfrac {f}{g}}\right)(x)}={\dfrac {f(c)}{g(c)}}$

当然，对于任何除法，g(c) 必须是一个有效数字，即不为 0。

这实际上是在您查看极限的代数运算保存证明时得出的推论。只需将极限值 *L* 和 *M* 分别替换为 ƒ(c) 和 g(c) 即可。

我们可以使用序列极限来证明函数不连续，方法如下

• $f(x)$ 在 $c$ 处不连续，当且仅当存在两个序列 $(x_{n})\rightarrow c$ 和 $(y_{n})\rightarrow c$ 使得 $\lim _{n\rightarrow \infty }(f(x_{n}))\not =\lim _{n\rightarrow \infty }(f(y_{n}))$.

复合

复合比较棘手，但它仍然像直觉暗示的那样起作用；两个连续函数的复合仍然是一个连续函数。

定理

---

如果 $f:B\rightarrow \mathbb {R}$ 在 $g(x)$ 的值域上是连续的，并且 $g:A\rightarrow B$ 在任何区间 $A$ 上是连续的，那么复合函数 $(f\circ g)(x)=f(g(x))$ 在 A 上是连续的。

证明过程简单地通过满足复合函数 $f$ 和 $g$ 的连续性定义来完成。因此，除了纯粹的定义之外，没有使用代数或定理。

证明复合函数在 c 处连续

首先，我们知道连续性需要什么。因此，我们将使用最基本满足连续性要求的定义来定义 epsilon。	令 $\epsilon >0$
由于 f 必须是连续的，我们也写下我们知道是真的——它满足连续性的属性清单。现在，我们将对 delta 变量进行一些修改，原因将在后面解释。	$\exists \delta _{1}>0:|x-c|<\delta _{1}\implies |f(x)-f(c)|<\epsilon$.
但是，$f$ 还有更多属性。关键的是 $c$ 和 $x$ 指的是什么。由于函数 $f$ 在 $g(x)$ 的值域上是连续的，这意味着 $f$ 的输入值实际上是 $g$ 的输出值。因此，我们可以用 $g(x)$ 的输出值有效地替换 $f$ 中的 $c$ 和 $x$ 的值。	$\exists \delta _{1}>0:|g(x)-g(c)|<\delta _{1}\implies |f\circ g(x)-f\circ g(c)|<\epsilon$.
由于 g 必须是连续的，我们也会写下我们知道为真的内容，即连续性的定义。	$\exists \delta _{2}>0:|x-c|<\delta _{2}\implies |g(x)-g(c)|<\epsilon$.
表达式 $|g(x)-g(c)|<\epsilon$ 和 $|g(x)-g(c)|<\delta _{1}$ 非常相似。我们可以利用这一点，看看是否可以利用我们知道的任何性质。 考虑到 $\epsilon$ 的唯一要求是它必须为正，并且它的不等式关系对任何数字都成立，并且 $\delta _{1}$ 为正且是一个数字，那么我们可以将二者联系起来，并定义 $\epsilon$ 为 $\delta _{1}$。	令 $\epsilon =\delta _{1}$
因此，我们抽象地将一个基于我们知道为真的内容构建的连续性定义串联起来；即 $f$ 和 $g$ 的连续性。阅读这个新蕴涵语句的有效结果；即 $f$ 和 $g$ 的复合函数的连续性，我们确信我们的说法，即 $f$ 和 $g$ 的复合函数也是连续的。证毕。	因此 $|x-c|<\delta _{2}\implies |g(x)-g(c)|<\delta _{1}\implies |f(g(x))-f(g(c))|<\epsilon$ 所以 $f\circ g(x)$ 在 A 上是连续的。
$\square$

三个连续性定理

考虑一下连续性的直观概念。如果你不能想象一个多项式函数的图像，它总是起作用的。当曲线平滑地穿过函数的定义域时，它就是连续性的图形表示。然而，我们如何从数学上知道它是连续的呢？好吧，我们将从三个连续性定理开始，这些定理将验证这个概念。

介值定理

这是关于连续性的一个重要定理。它本质上表明连续函数没有突然的跳跃或断裂。

定理

---

设 f(x) 是一个连续函数。如果 $a<b$ 且 $f(a)<m<f(b)$，则 $\exists c\in (a,b):f(c)=m$.

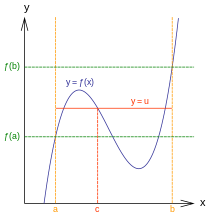介值定理：给定一个在 [a,b] 上连续的函数，以及三个变量 a < c < b，则必须有 ƒ(a) < ƒ(c) < ƒ(b)

证明

设 $S=\{x\in (a,b):f(x)<m\}$，设 $c=\sup S$.

设 $\epsilon =|f(c)-m|$。根据连续性，$\exists \delta :|x-c|<\delta \implies |f(x)-f(c)|<\epsilon$.

如果 f(c) < m，那么 $|f(c+{\frac {\delta }{2}})-f(c)|<\epsilon$，所以 $f(c+{\frac {\delta }{2}})<f(c)+\epsilon =m$。但然后 $c+{\frac {\delta }{2}}\in S$，这意味着 c 不是 S 的上界，矛盾。

如果 f(c) > m，那么由于 $c=\sup S$，$\exists x:x\in S,c>x>c-\delta$。但由于 $|x-c|<\delta$，$|f(x)-f(c)|<\epsilon$，所以 $f(x)>f(c)-\epsilon$ = m，这意味着 $x\notin S$，矛盾。 $\Box$

我们现在将证明最小-最大定理，这是另一个与连续性相关的重大结果。本质上，它指出闭区间上的任何连续映射都是有界的，并且它也取得了这些界限。

最小-最大定理

该定理是另一个较大定理的第一部分。但是，就其本身而言，它有助于弥合关于函数的上确界和下确界之间的差距。

定理

---

给定一个在 [a,b] 上的连续函数 ƒ，即 $f:[a,b]\to \mathbb {R}$，那么 $f([a,b])$ 是有界的。

证明

假设如果可能的话，$f$ 是无界的。

令 $x_{1}={\tfrac {a+b}{2}}$。 然后，$f$ 在至少一个闭区间 $[a,x_{1}]$ 和 $[x_{1},b]$ 上无界（否则，$f$ 在 $[a,b]$ 上有界，这与假设矛盾）。 将此区间称为 $I_{1}$。

类似地，将 $I_{1}$ 分成两个闭区间，并令 $I_{2}$ 是 $f$ 无界的那个区间。

因此，我们得到一个嵌套闭区间的序列 $[a,b]\supseteq I_{1}\supseteq I_{2}\supseteq \ldots$，使得 $f$ 在每个区间上都是无界的。

我们知道，一个嵌套闭区间序列的交集是非空的。 因此，令 $x_{0}\in I_{1}\cap I_{2}\cap \ldots$

因为 $f(x)$ 在 $x=x_{0}$ 处连续，所以存在 $\delta >0$ 使得 $x\in V_{\delta }(x_{0})\implies f(x)\in (f(x_{0})-1,f(x_{0})+1)$ 但根据定义，总存在 $k\in \mathbb {N}$ 使得 $I_{k}\subseteq V_{\delta }(x_{0})$，与 $f$ 在 $I_{k}$ 上无界假设矛盾。因此，$f$ 在 $[a,b]$ 上有界。

极值定理

这是定理的第二部分。它比之前的定理更具论断性，说明不仅存在上确界和下确界，而且它们也可以被函数ƒ取到，并且位于您指定的区间内。

定理

---

对于在 [a,b] 上连续的函数ƒ，即 $f:[a,b]\to \mathbb {R}$，如果 $M,m$ 分别是 $f([a,b])$ 的上界和下界，则存在 $c,d\in [a,b]$ 使得 $f(c)=M,f(d)=m$。

极值定理的描述：对于在 [a,b] 上连续的函数，一定存在最大值点 c 和 d，使得 ƒ(c) 是区间内的最大值，ƒ(d) 是区间内的最小值。

证明

假设如果可能，$M=\sup(f([a,b]))$ 但 $M\notin f([a,b])$.

考虑函数 $g(x)={\frac {1}{M-f(x)}}$. 由连续性的代数性质，$g:[a,b]\to \mathbb {R}$ 是连续的。然而，$M$ 是 $f([a,b])$ 的聚点，$g(x)$ 在 $[a,b$ 上无界，与 (i) 矛盾。因此，$M\in f([a,b])$。类似地，我们可以证明 $m\in f([a,b])$.

附录

连续性将在数学的其他分支中再次出现。您不仅会遇到连续性的不同变体，还会遇到连续性的不同定义。

一致连续性

令 $A\subseteq \mathbb {R}$
令 $f:A\to \mathbb {R}$

我们说 $f$ 在 $A$ 上是一致连续的，当且仅当对于每个 $\varepsilon >0$ 存在 $\delta >0$ 使得如果 $x,y\in A$ 且 $|x-y|<\delta$，那么 $|f(x)-f(y)|<\varepsilon$

Lipschitz 连续性

令 $A\subseteq \mathbb {R}$
令 $f:A\to \mathbb {R}$

我们说 $f$ 在 $A$ 上是Lipschitz 连续的，当且仅当存在一个正实数常数 $K$ 使得，对于所有 $x,y\in A$，$|f(x)-f(y)|\leq K|x-y|$.

最小的这样的 $K$ 被称为函数 $f$ 的Lipschitz 常数。

拓扑连续性

如前所述，连续函数的概念被应用于数学的许多领域，特别是在拓扑学中。在这种情况下，连续性的另一种表征非常有用。

定理

令 $A\subseteq \mathbb {R}$
令 $f:A\to \mathbb {R}$

$f(x)$ 在 $x=c$ 处连续当且仅当对于 $f(x)$ 的每一个开邻域 $V$，都存在 $x$ 的一个开邻域 $U$，使得 $U\subseteq f^{-1}(V)$

需要注意的是，“开集”这个概念可以在比实数集或度量空间更一般的环境下定义，因此这种描述方式具有很高的实用性。