三角函数/三角方程求解

三角方程包含三角函数的方程。如果它们只包含这些函数和常数，那么解法需要找到一个未知数，它是三角函数的参数。

基本三角方程

sin(x) = n

$n$	$\sin(x)=n$
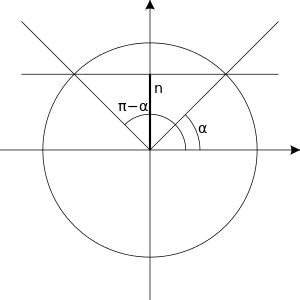
$|n|<1$	${\begin{matrix}x=\alpha +2k\pi \\x=\pi -\alpha +2k\pi \\\alpha \in \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]\end{matrix}}$
$n=-1$	$x=-{\begin{matrix}{\frac {\pi }{2}}\end{matrix}}+2k\pi$
$n=0$	$x=k\pi$
$n=1$	$x={\begin{matrix}{\frac {\pi }{2}}\end{matrix}}+2k\pi$
$|n|>1$	$x\in \varnothing$

方程 $\sin(x)=n$ 只有在 $n$ 在区间 $[-1,1]$ 内时才有解。如果 $n$ 在此区间内，那么我们首先找到一个 $\alpha$ 使得

$\alpha =\arcsin(n)$

那么解就是

$x=\alpha +2k\pi$

$x=\pi -\alpha +2k\pi$

其中 $k$ 是整数。

在 $n$ 等于 1、0 或 -1 的情况下，这些解有更简单的形式，总结在右侧的表格中。

例如，要解

$\sin {\bigl (}{\tfrac {x}{2}}{\bigr )}={\frac {\sqrt {3}}{2}}$

首先找到 $\alpha$ 

$\alpha =\arcsin {\bigl (}{\tfrac {\sqrt {3}}{2}}{\bigr )}={\frac {\pi }{3}}$

然后代入上面的公式

${\frac {x}{2}}={\frac {\pi }{3}}+2k\pi$

${\frac {x}{2}}=\pi -{\frac {\pi }{3}}+2k\pi$

解出关于 $x$ 的线性方程得到最终答案

$x={\frac {2\pi }{3}}(1+6k)$

$x={\frac {4\pi }{3}}(1+3k)$

其中 $k$ 是整数。

cos(x) = n

$n$	$\cos(x)=n$
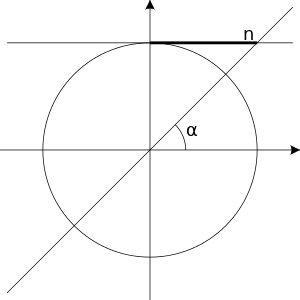
$|n|<1$	${\begin{matrix}x=\pm \alpha +2k\pi \\\alpha \in [0,\pi ]\end{matrix}}$
$n=-1$	$x=\pi +2k\pi$
$n=0$	$x={\begin{matrix}{\frac {\pi }{2}}\end{matrix}}+k\pi$
$n=1$	$x=2k\pi$
$|n|>1$	$x\in \varnothing$

与正弦方程类似，形如$\cos(x)=n$ 的方程只有当n在区间$[-1,1]$ 内时才有解。为了解这样的方程，我们首先要找到一个角度$\alpha$ 使得

$\alpha =\arccos(n)$

然后，$x$ 的解为

$x=\pm \alpha +2k\pi$

其中 $k$ 是整数。

当$n$ 等于 1、0 或 -1 时，更简单的案例总结在右侧表格中。

tan(x) = n

$n$	$\tan(x)=n$
一般情况 情况	${\begin{matrix}x=\alpha +k\pi \\\alpha \in \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]\end{matrix}}$
$n=-1$	$x=-{\begin{matrix}{\frac {\pi }{4}}\end{matrix}}+k\pi$
$n=0$	$x=k\pi$
$n=1$	$x={\begin{matrix}{\frac {\pi }{4}}\end{matrix}}+k\pi$

形如$\tan(x)=n$ 的方程对于任何实数$n$ 都有解。为了找到它们，我们必须首先找到一个角度$\alpha$ 使得

$\alpha =\arctan(n)$

找到 $\alpha$ 后，$x$ 的解为

$x=\alpha +k\pi$

当 $n$ 等于 1、0 或 -1 时，解的形式更简单，如右侧表格所示。

cot(x) = n

$n$	$\cot(x)=n$
一般情况 情况	${\begin{matrix}x=\alpha +k\pi \\\alpha \in \left[0;\pi \right]\end{matrix}}$
$n=-1$	$x=-{\begin{matrix}{\frac {3\pi }{4}}\end{matrix}}+k\pi$
$n=0$	$x={\begin{matrix}{\frac {\pi }{2}}\end{matrix}}+k\pi$
$n=1$	$x={\begin{matrix}{\frac {\pi }{4}}\end{matrix}}+k\pi$

方程 $\cot(x)=n$ 对于任何实数 $n$ 都有解。为了找到它们，我们必须首先找到一个角 $\alpha$，使得

$\alpha =\operatorname {arccot}(n)$

找到 $\alpha$ 后，$x$ 的解为

$x=\alpha +k\pi$

当 $n$ 等于 1、0 或 -1 时，解的形式更简单，如右侧表格所示。

csc(x) = n 以及 sec(x) = n

三角方程 $\csc(x)=n$ 以及 $\sec(x)=n$ 可以通过将其转换为其他基本方程来求解

$\csc(x)=n\ \Leftrightarrow \ {\frac {1}{\sin(x)}}=n\ \Leftrightarrow \ \sin(x)={\frac {1}{n}}$

$\sec(x)=n\ \Leftrightarrow \ {\frac {1}{\cos(x)}}=n\ \Leftrightarrow \ \cos(x)={\frac {1}{n}}$

更多例子

一般来说，为了解决三角方程，我们必须首先使用三角恒等式将它们转化为基本三角方程。本节列出了一些常见的示例。

a sin(x)+b cos(x) = c

为了解决这个方程，我们将使用以下恒等式：

$a\sin(x)+b\cos(x)={\sqrt {a^{2}+b^{2}}}\sin(x+\alpha )$

$\alpha ={\begin{cases}\arctan {\bigl (}{\frac {b}{a}}{\bigr )},&{\mbox{if }}a>0\\\pi +\arctan {\bigl (}{\frac {b}{a}}{\bigr )},&{\mbox{if }}a<0\end{cases}}$

该方程变为：

${\sqrt {a^{2}+b^{2}}}\sin(x+\alpha )=c$

$\sin(x+\alpha )={\frac {c}{\sqrt {a^{2}+b^{2}}}}$

该方程的形式为 $\sin(x)=n$，可以使用上面给出的公式求解。

例如，我们将解决：

$\sin(3x)-{\sqrt {3}}\cos(3x)=-{\sqrt {3}}$

在这种情况下，我们有：

$a=1,b=-{\sqrt {3}}$

${\sqrt {a^{2}+b^{2}}}={\sqrt {1^{2}+{\Big (}-{\sqrt {3}}{\Big )}^{2}}}=2$

$\alpha =\arctan {\Big (}-{\sqrt {3}}{\Big )}=-{\frac {\pi }{3}}$

应用恒等式：

$2\sin \left(3x-{\frac {\pi }{3}}\right)=-{\sqrt {3}}$

$\sin \left(3x-{\frac {\pi }{3}}\right)=-{\frac {\sqrt {3}}{2}}$

因此，根据 $\sin(x)=n$ 的公式，方程的解为

$3x-{\frac {\pi }{3}}=-{\frac {\pi }{3}}+2k\pi \ \Leftrightarrow \ x={\frac {2k\pi }{3}}$

$3x-{\frac {\pi }{3}}=\pi +{\frac {\pi }{3}}+2k\pi \ \Leftrightarrow \ x={\frac {\pi }{9}}(6k+5)$

其中 $k$ 是整数。