波动/费马原理

波动 : 几何光学
1 - 2 - 3 - 4 - 5 - 6
问题

费马原理

费马原理可以用来发展几何光学的一种替代方法。该原理（以最简单的形式）指出，给定频率的光波在两点之间传播的路径需要最短的时间。最明显的例子是光穿过均匀介质，其中光速不会随位置变化。在这种情况下，最短时间等效于两点之间的最短距离，众所周知，这条线是一条直线。因此，费马原理与光在均匀介质中沿直线传播是一致的。

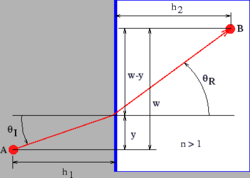
费马原理也可以用来推导出反射和折射定律。例如，图 3.10 显示了反射光线的候选光线，其中入射角和反射角不相等。光从 A 点传播到 B 点所需的时间为

t=[\{h_{1}^{2}+y^{2}\}^{1/2}+\{h_{2}^{2}+(w-y)^{2}\}^{1/2}]/c

(4.12)

其中 $c$ 是光速。我们通过对 $t$ 关于 $y$ 进行微分，并将结果设为零，得到

{\frac {y}{\{h_{1}^{2}+y^{2}\}^{1/2}}}={\frac {w-y}{\{h_{2}^{2}+(w-y)^{2}\}^{1/2}}}.

(4.13)

然而，我们注意到这个等式的左侧仅仅是 $\sin \theta _{I}$ ，而右侧是 $\sin \theta _{R}$ ，因此最小时间条件简化为 $\sin \theta _{I}=\sin \theta _{R}$ 或 $\theta _{I}=\theta _{R}$ ，这就是反射定律。

类似的分析可以用来推导出斯涅尔折射定律。光在折射率为 $n$ 的介质中的速度为 $c/n$ ，其中 $c$ 是其在真空中的速度。因此，光在该介质中传播一定距离所需的时间是 $n$ 倍于光在真空中传播相同距离所需的时间。参考图3.11，光从A到B所需的时间变为

t=[\{h_{1}^{2}+y^{2}\}^{1/2}+n\{h_{2}^{2}+(w-y)^{2}\}^{1/2}]/c.

(4.14)

这导致了以下条件：

\sin \theta _{I}=n\sin \theta _{R}

(4.15)

其中 $\theta _{R}$ 现在是折射角。我们识别出这个结果是斯涅尔定律。

请注意，反射案例说明了关于费马原理的一点：最小时间实际上可能是局部最小值而不是全局最小值——毕竟，在图3.10中，从A到B的全局最小距离仍然只是两点之间的直线！实际上，从点A开始的光将通过两条路径到达点B——直线路径和反射路径。

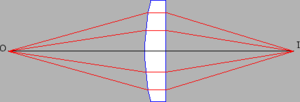
图3.13说明了一种相当奇特的情况。请注意，从点O发出并与透镜相交的所有光线最终都落在了点I上。这似乎与费马原理相矛盾，因为只有最小（或最大）时间轨迹应该出现。然而，计算表明，在这个特定情况下，所有说明的轨迹都花费了相同的时间。因此，光不能使用费马原理选择一条轨迹而不是另一条，所有轨迹都同样有利。请注意，这个推论并不适用于任何轨迹集合，而只适用于从一个焦点到另一个焦点的轨迹集合。

波动 : 几何光学
1 - 2 - 3 - 4 - 5 - 6
问题