有时你无法找到精确答案,只能找到答案所在范围的估计值。这个答案,以及合适的 **误差界限**,是可以接受的,并且经常用于实验数据,因为在实验数据中,高度的精确性并不总是合理。
如果你被告知某扇门高 2 米,你可以假设这扇门的高度可以在 1.5 米到 2.5 米之间,用 **不等式**  表示,并且实际上是四舍五入到 2 米的。如果你被告知同一扇门高 2.0 米,那么你可以假设更高的精确度,并说这扇门的高度在 1.95 米到 2.05 米之间,用不等式
表示,并且实际上是四舍五入到 2 米的。如果你被告知同一扇门高 2.0 米,那么你可以假设更高的精确度,并说这扇门的高度在 1.95 米到 2.05 米之间,用不等式  表示。在这里你会说门的高度是 2 米,**误差界限**为
表示。在这里你会说门的高度是 2 米,**误差界限**为  。这意味着实际值在声明值的 0.05m 之内。如果你没有得到测量值的误差界限,你应该假设最后一个数字是四舍五入的,并将所有其他数字视为准确的。
。这意味着实际值在声明值的 0.05m 之内。如果你没有得到测量值的误差界限,你应该假设最后一个数字是四舍五入的,并将所有其他数字视为准确的。
门的实际高度的最小值和最大值被称为 **下界** 和 **上界**,用于确定测量的精度。
**绝对误差** 是获得的值和真实值之间的差值。测量的绝对误差可以使用以下公式找到

**相对误差** 是绝对误差占真实值的比例。测量的相对误差可以使用以下公式找到

**百分比误差** 是绝对误差占真实值的百分比。测量的百分比误差可以使用以下公式找到

例如,如果 2 米门的真实值为 1.95 米,则绝对误差为 ,相对误差为
,相对误差为 ,百分比误差为
,百分比误差为 .
.
不等式是比较点、线或曲线的相对大小的表达式。与等式不同,等式两边始终相等,不等式可以有一边大于或等于另一边。
主要有四个基本符号
 小于,
小于, 大于,
大于, 小于或等于,以及
小于或等于,以及 大于或等于。
大于或等于。
例如, 表示
表示 小于 4,
小于 4, 表示
表示 大于 4,
大于 4, 表示
表示 等于 4 或小于 4 的任何数字,而
等于 4 或小于 4 的任何数字,而 表示
表示 等于 4 或大于 4 的任何数字。
等于 4 或大于 4 的任何数字。
注意 和
和 本质上是相同的陈述。
本质上是相同的陈述。
如果您对哪个符号表示小于和大于是感到困惑,那么记住不等式符号始终指向较小的数字会很有帮助。要记住的一条基本规则是,如果除以或乘以负数,不等式符号就会反转。例如 将变为
将变为 。这是有道理的,因为 -4 大于 -5,而 5 大于 4。
。这是有道理的,因为 -4 大于 -5,而 5 大于 4。
在某些情况下,两个不等式可以合并成一个。例如,门的高度据说在  和
和  之间。通常的写法是
之间。通常的写法是  。注意不等号的方向是一致的。
。注意不等号的方向是一致的。  是完全可以接受的,但将方向相反的不等式合并是不正确的,必须将它们作为两个独立的不等式保留。
是完全可以接受的,但将方向相反的不等式合并是不正确的,必须将它们作为两个独立的不等式保留。
为了解线性不等式,只需将 x 隔离。例如: 


注意符号的变化。
为了解二次不等式,我们需要:1)将不等式设为零。
2)因式分解方程并找到零点。
3)用方程的零点作为唯一点建立数轴。在这些点之间建立区间。
4)找到因式的符号。然后找到方程在区间上的符号。
5)满足不等式的区间是你的答案集。
例如:找到满足关系  的区间。
的区间。
步骤 1:
步骤 2: ,因此零点将是 -1 和 5
,因此零点将是 -1 和 5
步骤 3
编辑:需要新的图片来显示中间列为:x 大于或等于 -1 且小于或等于 5。
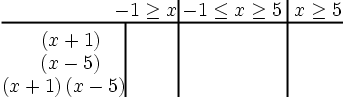
步骤 4:
步骤 5:满足该关系的区间是  和
和  。这是解集。
。这是解集。
解涉及分数的方程与解二次不等式非常相似。当您解涉及分数的不等式时,不能交叉相乘(因为您可能在乘以一个负数,这将反转不等式的符号)。这将导致错误的答案。还要记住,分母永远不能为零。
例如:找到满足关系  的区间。
的区间。
步骤 1: 将  简化后得到
简化后得到  .
.
步骤 2: 已经因式分解,所以零点为 -1 和 5。
步骤 3:
步骤 4:
步骤 5: 满足关系式的区间是  和
和  ,因此
,因此  。注意,
。注意, 大于是因为 x 不能等于 -1,否则分母将为零。
大于是因为 x 不能等于 -1,否则分母将为零。
区间表示法是另一种写不等式问题的解集区间的方法。应该使用区间表示法给出答案,因为它更容易理解。在区间表示法中,解集用括号给出。使用两种类型的括号:
( ) 这类括号表示端点不包含在解集中。  和
和 
[ ] 这类括号表示端点包含在解集中。  和
和 
还可以使用这些括号的各种组合。如果有多个区间,需要使用数学并集符号  。此外,如果区间到达
。此外,如果区间到达  ,则需要使用圆括号 ),因为
,则需要使用圆括号 ),因为  是一个概念,而不是一个数字。
是一个概念,而不是一个数字。
例如,将  转换为区间表示法。
转换为区间表示法。
在区间表示法中,解集变为 ![{\displaystyle \left(-\infty ,-4\right)\cup \left[-3,7\right)\cup \left(8,9\right]\cup \left[12,\infty \right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5d111db3b2d335b733e41291e8825ab741bc9ea) ,正如您所见,这更容易理解。
,正如您所见,这更容易理解。
















































![{\displaystyle \left(-\infty ,-4\right)\cup \left[-3,7\right)\cup \left(8,9\right]\cup \left[12,\infty \right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5d111db3b2d335b733e41291e8825ab741bc9ea)