坐标是描述位置的一种方式。 在二维中,位置由两个垂直方向给出,即 *x* 和 *y*。
直线具有固定的斜率。 直线的斜率及其 y 轴截距是区分一条直线与另一条直线的两个信息。
直线最常见的形式是 y = mx + c。 m 是直线的斜率,c 是直线与 y 轴的交点。 当 c 为 0 时,直线通过原点 (0,0)。 方程的其他形式为 x = a,用于无限斜率的垂直线,y = b 用于斜率为零的水平线。 此外,一些方程通常写为:px + qy + c = 0。 您也可以使用方程 y-y1=m(x-x1)
直线的陡峭程度可以通过其斜率来衡量,斜率是 y 方向的变化量除以 x 方向的变化量。 字母 m 用于表示斜率。 求斜率的公式为:  作为旁注
作为旁注  .
.
斜率为 m 且经过坐标  的直线方程为:
的直线方程为:  。 然后只需将方程重新排列成 y = mx + c 的形式。
。 然后只需将方程重新排列成 y = mx + c 的形式。
如果一对直线的斜率相等,则它们平行(符号为  )。 如果它们的斜率相等,则
)。 如果它们的斜率相等,则  。 因此,为了找到平行线的方程,您需要原始线的斜率和平行线上的一组坐标。 然后使用点斜式来找到平行线的方程。
。 因此,为了找到平行线的方程,您需要原始线的斜率和平行线上的一组坐标。 然后使用点斜式来找到平行线的方程。
两条直线互相垂直(符号为  ),如果它们的斜率乘积为
),如果它们的斜率乘积为  。因此,如果你需要一条垂直于另一条直线的直线的方程,你只需要用 m 的负倒数替换斜率 m。
。因此,如果你需要一条垂直于另一条直线的直线的方程,你只需要用 m 的负倒数替换斜率 m。
例如,如果直线 1 为 y = 2x + 3,并且你需要找到一条通过点 (0, 1) 的垂直于它的直线,那么斜率 m = -1/2(因为 2 x -1/2 = -1)。
这给出了 y = -x/2 +c。
将已知点 (0, 1) 代入此方程得到
1 = -0/2 +c,这给出了 c = 1
因此,方程为 y = 1 - x/2。
使用两点的坐标,可以使用勾股定理计算它们之间的距离。任意两点  和
和  之间的距离 d 由下式给出:
之间的距离 d 由下式给出:
当两点的坐标已知时,中点是这两点之间中点。对于任意两点 A 和 B
和 B ,AB 中点的坐标可以通过
,AB 中点的坐标可以通过  找到。
找到。
只要两条直线不平行,它们就会在一点相交。你可以通过简单地 联立方程 求解两个方程来找到交点。对于曲线也是如此,尽管非线性曲线可能在多个点相交或根本不相交,并且通常需要不同的方法来求解。
要绘制一条曲线的图形,你只需要知道曲线的形状以及其他重要的信息,如 x 轴和 y 轴的交点以及任何最大值和最小值的点。
 |

|
0 次 - 常数 -  或 或  。在本例中 y=2 。在本例中 y=2 |
1 次 - 线性 -  或 或  。在本例中 y = x。 。在本例中 y = x。 |
 |
|
二次函数 - 二次方 -  . 在这种情况下 y = . 在这种情况下 y =  |
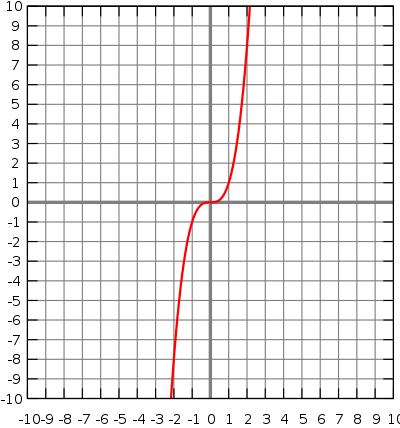
三次函数 - 立方 -  . 在这种情况下 y = . 在这种情况下 y =  |
注意: 所有  的奇数次方具有相同的形状,从左下角到右上角,所有
的奇数次方具有相同的形状,从左下角到右上角,所有  的偶数次方具有相同的“桶状”曲线。
的偶数次方具有相同的“桶状”曲线。
就像前面一样,具有  偶数次方的所有曲线具有相同的形状,具有
偶数次方的所有曲线具有相同的形状,具有  奇数次方的曲线具有另一种形状。
奇数次方的曲线具有另一种形状。
 |

|
 |

|
 |

|
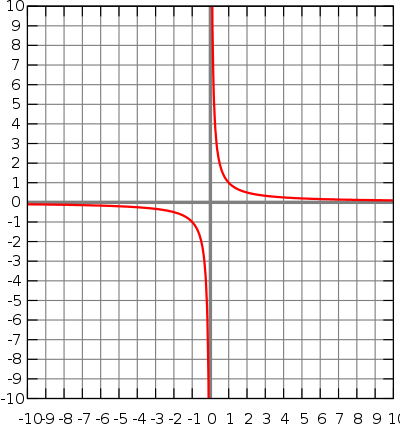
这种形式的所有曲线都没有  的值,因为
的值,因为  是未定义的。在
是未定义的。在  轴上有渐近线,曲线越来越缓慢地向 y 轴移动,但永远不会真正接触到。
轴上有渐近线,曲线越来越缓慢地向 y 轴移动,但永远不会真正接触到。

这种形式的所有曲线都没有 x < 0 的值。它们都具有相同的形状。
当一条直线与一条曲线相交时,可以通过将直线的方程代入曲线的方程来找到交点。如果直线形如  ,那么你可以用
,那么你可以用  替换任何
替换任何  的实例,然后展开方程,然后因式分解得到的二次方程。
的实例,然后展开方程,然后因式分解得到的二次方程。
需要有关描述曲线和直线之间几何关系的信息
可以使用与直线和曲线相同的方法。但是,它只适用于简单的情况。当代数方法失效时,需要求助于图形方法或数值方法。在考试中,你只需要使用代数方法。
在许多情况下,使用这些规则可以很容易地从现有图形获得新图形。
 是
是  关于 x 轴的对称图形。
关于 x 轴的对称图形。 是
是  关于 y 轴的对称图形。
关于 y 轴的对称图形。
 如果
如果  则远离 y 轴拉伸,如果
则远离 y 轴拉伸,如果  则向 y 轴拉伸。在这两种情况下,变化幅度为 b 个单位。
则向 y 轴拉伸。在这两种情况下,变化幅度为 b 个单位。 如果
如果  则向 x 轴拉伸,如果
则向 x 轴拉伸,如果  则远离 x 轴拉伸。在这两种情况下,变化幅度为 a 个单位。
则远离 x 轴拉伸。在这两种情况下,变化幅度为 a 个单位。
 是将 f(x) 向右平移 h 个单位后的图形。
是将 f(x) 向右平移 h 个单位后的图形。 是将 f(x) 向左平移 h 个单位后的图形。
是将 f(x) 向左平移 h 个单位后的图形。 是将 f(x) 向上平移 k 个单位后的图形。
是将 f(x) 向上平移 k 个单位后的图形。 是将 f(x) 向下平移 k 个单位后的图形。
是将 f(x) 向下平移 k 个单位后的图形。
圆形是平面中所有与给定点(称为圆心)距离为定值 r 的点的集合。距离 r 是圆形的半径。

圆形的两个基本定律是


如果半径垂直于弦,那么半径将平分该弦。

如果圆周上的任意一点与直径连接,则会形成一个直角三角形。

如果画出半径,然后从该点画出切线,那么半径和切线将相互垂直。

圆的标准方程为

这将始终得到一个以原点 (0,0) 为中心的圆。如果我们想要一个以 (h,k) 为中心的圆,则使用以下公式。

但是你不能用计算器绘制这两个方程。你需要将它分成两个方程,但图将不完美,因为当 x = 0 和  :
:  和
和  时,x 未定义。
时,x 未定义。
以下是  的图形。
的图形。




































































