微积分/空间中的曲线和曲面

← 向量	微积分	多元微积分 →
	空间中的曲线和曲面

对于许多实际应用，你必须使用直线、平面、曲线和曲面在三维空间中的数学描述。这需要一些关于向量的知识，以及在不使用计算器的情况下构建三维图形的能力。

三维空间中的直线

虽然直线的方程在前面的章节中讨论过（参见第7.1章），但本章将更详细地解释直线的性质和重要方面，以及扩展到三维空间中的一般曲线。

参数方程回顾

回想一下第5.1章，参数方程使用不同的变量来表达两个变量之间的关系。例如，看看下面的圆的方程

$x^{2}+y^{2}=1$

如果我们将变量 $x$ 和 $y$ 用一个新的变量 $t$ 表示，并且我们知道 $\cos ^{2}t+\sin ^{2}t=1$ ，我们可以将原始方程改写为

$x=\cos t$

$y=\sin t$

上面的方程是半径为 $1$ 的圆的参数形式。

现在，让我们谈谈三维空间中的直线。

三维空间中直线的方程

空间中的一条直线由空间中的两个点定义，我将它们称为 $P_{1}$ 和 $P_{2}$ 。令 $\mathbf {r} _{0}$ 为从原点到 $P_{1}$ 的向量， $\mathbf {r} _{2}$ 为从原点到 $P_{2}$ 的向量。给定这两个点，直线上的其他任何点 $P$ 可以通过以下方式到达

\mathbf {r} =\mathbf {r} _{0}+\mathbf {v} t

其中 $\mathbf {v}$ 是从 $P_{1}$ 到 $P_{2}$ 的向量

\mathbf {v} =\mathbf {r} _{0}-\mathbf {r} _{2}

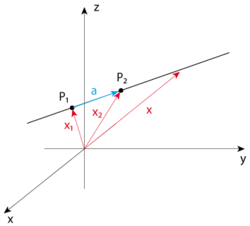
为了直观地理解直线的方程，想象有一条直线经过向量 $\mathbf {r} _{0}$ 的端点，并沿向量 $\mathbf {v}$ 的方向延伸。只需将其视为点斜式的一个向量版本。例如，假设在三维空间中有一条直线，其方程为

$\mathbf {r} =\langle 2,5,4\rangle +\langle 1,1,1\rangle t$

我们可以先找到点 $(2,5,4)$ ，然后将直线沿着向量 $\langle 1,1,1\rangle$ 平行方向拉伸。最终的图形是直线 $\mathbf {r} =\langle 2,5,4\rangle +\langle 1,1,1\rangle t$ 的图形。有时方向向量 $\mathbf {v}$ 未知。但是，我们可以通过找到直线上的另一个点来轻松求解。在本例中，点 $(5,8,7)$ 在直线上。通过计算两点之间的向量，我们可以发现方向向量是 $\langle 3,3,3\rangle$ 。因此，直线的方程可以写成

$\mathbf {r} =\langle 2,5,4\rangle +\langle 3,3,3\rangle t_{1}$

它等价于原始方程 $\mathbf {r} =\langle 2,5,4\rangle +\langle 1,1,1\rangle t$ ，因为如果我们令 $t=3t_{1}$ ，原始方程将变为上面的方程。因此，使用向量形式来写三维空间中直线的方程有无数种方法。现在，有一种参数形式可以表达直线。回想一下，还有另一种写向量的方法： $a\mathbf {i} +b\mathbf {j} +c\mathbf {k}$ 。因此，我们可以将原始方程 $\mathbf {r} =\langle 2,5,4\rangle +\langle 1,1,1\rangle t$ 重写为

$\mathbf {r} =\langle 2+t,5+t,4+t\rangle =(2+t)\mathbf {i} +(5+t)\mathbf {j} +(4+t)\mathbf {k}$

然后，我们将各个部分分配给相应的 $x,y,z$ 轴

$x=2+t$
$y=5+t$
$z=4+t$

这是直线方程的参数形式。

最后，表示直线的常用方法是使用对称方程，这只是参数形式的另一种微小变换。

$x-2=y-5=z-4$

概括地说，基本上有三种方法可以写出通过点 $(x_{0},y_{0},z_{0})$ 且方向为 $\langle a,b,c\rangle$ 的直线方程。

向量方程	参数方程	对称方程
$\mathbf {r} =\langle x_{0},y_{0},z_{0}\rangle +\langle a,b,c\rangle t$	$x=x_{0}+at$ $y=y_{0}+bt$ $z=z_{0}+ct$	${\frac {x-x_{0}}{a}}={\frac {y-y_{0}}{b}}={\frac {z-z_{0}}{c}}$

两条直线之间的关系

有些直线彼此相交，有些则不相交。直线可以是平行、垂直或相交的，这些将在本部分讨论。

交点

假设有两条直线，它们的方程为

$L_{1}:\langle 2,5,4\rangle +\langle 1,1,1\rangle t$ 或参数形式 $L_{1}:{\begin{cases}x=2+t\\y=5+t\\z=4+t\end{cases}}$

$L_{2}:\langle 5,-1,0\rangle +\langle -{\frac {1}{2}},4,3\rangle s$ 或参数形式 $L_{2}:{\begin{cases}x=5-{\frac {1}{2}}s\\y=-1+4s\\z=3s\end{cases}}$

要找出它们是否相交，我们只需要解这个方程组

${\begin{cases}2+t=5-{\frac {1}{2}}s\\5+t=-1+4s\\4+t=3s\end{cases}}$

如果方程组只有一个解，那么两条直线在一点相交。如果方程组有无穷多解，那么两条直线重合。如果方程组没有解，那么两条直线根本不相交。在本例中，有一个解

${\begin{cases}t=2\\s=2\end{cases}}$

因此，两条直线在点 $(4,7,6)$ 相交。如果我们想进一步了解两条直线之间的夹角，我们可以应用点积公式。两条直线之间的夹角应该为

$\theta =\arccos({\frac {\mathbf {v_{1}} \,\cdot \,\mathbf {v_{2}} }{\|\mathbf {v_{1}} \|\|\mathbf {v_{2}} \|}})$

平行

要发现三维空间中的两条平行直线，我们只需要查看方向向量 $\mathbf {v}$ 。如果两条直线 $\mathbf {v_{1}} ,\mathbf {v_{2}}$ 的方向向量满足关系 $\mathbf {v_{2}} =k\mathbf {v_{1}} ,k\in \mathbb {R}$ ，那么这两条直线互相平行。例如，两条直线 $L_{1}:\langle 2,5,4\rangle +\langle 1,1,1\rangle t$ 和 $L_{2}:\langle 5,-1,0\rangle +\langle -3,-3,-3\rangle s$ 互相平行，因为 ${\frac {\langle -3,-3,-3\rangle }{-3}}=\langle 1,1,1\rangle$ 。

垂直

要使两条直线互相垂直，这两条直线必须首先相交。如果它们确实相交，请回忆向量点积。点积指出

$\mathbf {a} \,\cdot \,\mathbf {b} =\|\mathbf {a} \|\|\mathbf {b} \|\cos \theta$

如果两条直线互相垂直，则 $\theta ={\frac {\pi }{2}}$ ，由此得出 $\mathbf {a} \,\cdot \,\mathbf {b} =\|\mathbf {a} \|\|\mathbf {b} \|\cos {\frac {\pi }{2}}=0$ 。

因此，如果我们继续这种思路，我们可以发现，如果我们在每条线上选择两个向量，对它们进行点积，结果为零，那么我们可以安全地说这两条线相互垂直。然而，有一个更方便的方法来简化这个过程。我们不需要在每条线上找到两个向量，而是只需要对两个方向向量应用点积，因为方向向量是从各自线上点计算出来的。

所以如果我们有两条直线

$L_{1}:\langle 2,5,4\rangle +\langle 1,1,1\rangle t$ 和 $L_{2}:\langle 6,6,5\rangle +\langle -2,1,1\rangle s$

它们相互垂直，因为

${\begin{cases}2+t=6-2s\\5+t=6+s\\4+t=5+s\end{cases}}$ 只有一个解： ${\begin{cases}t=2\\s=1\end{cases}}$ ，这意味着它们相交。而且 $\langle 1,1,1\rangle \,\cdot \,\langle -2,1,1\rangle =0$

因此结束了证明。

异面直线

异面直线是不相交且不平行的直线。例如，直线 $L_{1}:\langle 2,5,4\rangle +\langle 1,1,1\rangle t$ 和 $L_{2}:\langle 5,-1,0\rangle +\langle 3,-3,-3\rangle s$ 是异面直线。

两条异面直线之间的距离

要解决这个问题，我们需要了解三维空间中的平面，这将在下面讨论。

三维空间中的平面

介绍

相同的思想可以用来描述三维空间中的平面，它由空间中三个点（不在一条线上）唯一确定（ $P_{1},P_{2},P_{3}$ ）。设 $\mathbf {x} _{i}$ 为从原点到 $P_{i}$ 的向量。那么

\mathbf {x} =\mathbf {x} _{1}+\lambda \mathbf {a} +\mu \mathbf {b}

其中

\mathbf {a} =\mathbf {x} _{2}-\mathbf {x} _{1}\,\,{\text{and}}\,\,\mathbf {b} =\mathbf {x} _{3}-\mathbf {x} _{1}

注意，起点不一定要是 $\mathbf {x} _{1}$ ，可以是平面上的任何点。同样，向量 $\mathbf {a}$ 和 $\mathbf {b}$ 唯一的条件是它们必须是我们平面上的两个非共线向量。

回想一下，在二维向量中，如果有两个向量 $\mathbf {i} ,\mathbf {j}$ ，笛卡尔平面上的任何向量都可以用向量 $\mathbf {i} ,\mathbf {j}$ 表示为 $a\mathbf {i} +b\mathbf {j} \quad (a,b\in \mathbb {R} )$ 。使用相同的方法，我们可以推断出

the $\lambda \mathbf {a} +\mu \mathbf {b}$ 部分告诉我们图形应该是平面，而 $\mathbf {x} -\mathbf {x} _{1}$ 部分描述了“斜率”和轴交点

但是，还有两种方法可以表示三维空间中的平面：向量方程和标量方程。

平面的向量方程和标量方程

平面的向量方程要求我们理解点积的威力。我们已经知道，当两个向量的点积为零时，这两个向量应该相互垂直。现在，想象一个三维空间中的向量 $\mathbf {n}$ 。如果我们将所有与 $\mathbf {n}$ 垂直的向量 $\Delta \mathbf {r}$ 绘制出来，结果会是什么？

结果应该是具有垂直于平面的向量的平面。因此，平面的向量方程只是 $\mathbf {n} \,\cdot \,\Delta \mathbf {r} =0$ 。

向量 $\mathbf {n}$ 是法向量，它垂直于平面

向量 $\Delta \mathbf {r} =\mathbf {r} -\mathbf {r_{0}}$ 是变量向量，其中 $\mathbf {r} =\langle x,y,z\rangle$ （平面上未知点）以及 $\mathbf {r_{0}} =\langle x_{0},y_{0},z_{0}\rangle$ （平面上给定点）。这个表达式仅仅意味着平面上所有向量。

当然，平面向量方程可以改写为 $\mathbf {n} \,\cdot \,(\mathbf {r} -\mathbf {r_{0}} )=0$ 或者 $\mathbf {n} \,\cdot \,\mathbf {r} =\mathbf {n} \,\cdot \,\mathbf {r_{0}}$ ，这取决于作者。

要找到标量方程，我们只需要计算点积并进行一些简化。因此，假设

$\mathbf {n} =\langle a,b,c\rangle$ ， $\mathbf {r} =\langle x,y,z\rangle$ 以及 $\mathbf {r_{0}} =\langle x_{0},y_{0},z_{0}\rangle$ 根据向量方程
$\mathbf {n} \,\cdot \,(\mathbf {r} -\mathbf {r_{0}} )=0$
因此，我们有
$\langle a,b,c\rangle \,\cdot \,\langle x-x_{0},y-y_{0},z-z_{0}\rangle =0$
经过一些代数运算，我们可以得到
$ax+by+cz-(ax_{0}+by_{0}+cz_{0})=0$
由于 $ax_{0}+by_{0}+cz_{0}$ 是一个常数，我们令 $ax_{0}+by_{0}+cz_{0}=-d$ 。因此，平面的标量方程为 $ax+by+cz+d=0$

注意常数 $a,b,c$ 与法向量的 $\mathbf {i} ,\mathbf {j} ,\mathbf {k}$ 分量相同。这个性质在讨论两个平面的关系时非常有用。此外， $-d=\mathbf {n} \,\cdot \,\mathbf {r_{0}}$ 。

$\blacksquare$

总结一下，有三种方法可以表示三维空间中的平面，后两种更常用

从直线方程扩展	向量方程	标量方程
$\mathbf {x} =\mathbf {x} _{1}+\lambda \mathbf {a} +\mu \mathbf {b}$	$\mathbf {n} \,\cdot \,(\mathbf {r} -\mathbf {r_{0}} )=0$	$ax+by+cz+d=0$

两个平面的关系

平行

法向量很重要，因为它决定了平面的形状。因此，当我们讨论两个平面的关系时，实际上是在尝试找出两个平面的法向量之间的联系。在本例中，假设三维空间中有两个平面： $a_{1}x+b_{1}y+c_{1}z+d_{1}=0$ 和 $a_{2}x+b_{2}y+c_{2}z+d_{2}=0$ 。这两个平面的法向量应该是

$\mathbf {n_{1}} =\langle a_{1},b_{1},c_{1}\rangle ,\,\mathbf {n_{2}} =\langle a_{2},b_{2},c_{2}\rangle$

由于法向量与其对应的平面垂直，如果法向量彼此平行，那么它们对应的平面也应该彼此平行。因此，

如果 $\mathbf {n_{1}} =k\mathbf {n_{2}} \quad (k\in \mathbb {R} )$ ，那么 $a_{1}x+b_{1}y+c_{1}z+d_{1}=0$ 和 $a_{2}x+b_{2}y+c_{2}z+d_{2}=0$ 彼此平行。

垂直

如果法向量互相垂直，则它们所在的平面也互相垂直。换句话说，如果 $\mathbf {n_{1}} \perp \mathbf {n_{2}}$ ，那么这两个平面互相垂直。

交点

为了完全理解如何找到两条直线的交点，我们应该熟悉法向量及其潜在的应用。如果两个平面不平行，并且不是同一个平面，那么它们必须互相交叉。交点应该形成一条直线。想象一下，有两个平面 $a_{1}x+b_{1}y+c_{1}z+d_{1}=0$ 和 $a_{2}x+b_{2}y+c_{2}z+d_{2}=0$ ，它们的各自的法向量 $\mathbf {n_{1}} \neq k\mathbf {n_{2}} \quad (k\in \mathbb {R} )$ （这意味着它们不平行）。

因为法向量与平面上所有向量完全垂直，所以反过来也成立：平面上所有向量都与它们各自的法向量垂直。这就是 $\mathbf {n} \,\cdot \,(\mathbf {r} -\mathbf {r_{0}} )=0$ 是平面向量方程的原因。由于两个平面的交点是一条直线，我们可以说方向向量 $\mathbf {v}$ 应该在这两个平面上。

因为 $\mathbf {v}$ 位于两个平面上， $\mathbf {v}$ 应该与两个法向量垂直。
$\mathbf {v} \perp \mathbf {n_{1}} ,\,\mathbf {v} \perp \mathbf {n_{2}}$
回想一下，两个向量的叉积将产生一个新的向量，该向量与这两个原始向量都垂直。我们可以计算 $\mathbf {n_{1}} ,\mathbf {n_{2}}$ 的叉积来创建 $\mathbf {v}$ 。
$\mathbf {n_{1}} \times \mathbf {n_{2}} ={\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\a_{1}&b_{1}&c_{1}\\a_{2}&b_{2}&c_{2}\end{vmatrix}}=(b_{1}c_{2}-b_{2}c_{1})\mathbf {i} -(a_{1}c_{2}-a_{2}c_{1})\mathbf {j} +(a_{1}b_{2}-a_{2}b_{1})\mathbf {k}$
因此，这条线的方向向量为 $\mathbf {v} =\mathbf {n_{1}} \times \mathbf {n_{2}} =\langle b_{1}c_{2}-b_{2}c_{1},a_{1}c_{2}-a_{2}c_{1},a_{1}b_{2}-a_{2}b_{1}\rangle$

我们还需要知道直线上的一点来完成方程式，因为 $\mathbf {r} =\mathbf {r} _{0}+\mathbf {v} t$ 。要找到一个点，只需设 $z=0$ ，然后在以下方程组中求解 $x,y$
${\begin{cases}a_{1}x+b_{1}y+d_{1}=0\\a_{2}x+b_{2}y+d_{2}=0\end{cases}}\Rightarrow {\begin{cases}x={\frac {b_{1}d_{2}-b_{2}d_{1}}{a_{1}b_{2}-a_{2}b_{1}}}\\y={\frac {a_{1}d_{2}-a_{2}d_{1}}{a_{2}b_{1}-a_{1}b_{2}}}\end{cases}}$
由于解过于复杂，无法写下来，我们将让 $x={\frac {b_{1}d_{2}-b_{2}d_{1}}{a_{1}b_{2}-a_{2}b_{1}}}=x_{0}$ 以及 $y={\frac {a_{1}d_{2}-a_{2}d_{1}}{a_{2}b_{1}-a_{1}b_{2}}}=y_{0}$ 。因此，点 $(x_{0},y_{0},0)$ 同时位于两个平面（回想一下，我们令 $z=0$ ）上，并且 $\mathbf {P_{0}} =\langle x_{0},y_{0},0\rangle$ .

现在，我们知道直线 $(x_{0},y_{0},0)$ 上的一个点以及方向向量 $\mathbf {v} =\mathbf {n_{1}} \times \mathbf {n_{2}} =\langle b_{1}c_{2}-b_{2}c_{1},a_{1}c_{2}-a_{2}c_{1},a_{1}b_{2}-a_{2}b_{1}\rangle$ ，这两个平面的交线是： $L:\langle {\frac {b_{1}d_{2}-b_{2}d_{1}}{a_{1}b_{2}-a_{2}b_{1}}},{\frac {a_{1}d_{2}-a_{2}d_{1}}{a_{2}b_{1}-a_{1}b_{2}}},0\rangle +\langle b_{1}c_{2}-b_{2}c_{1},a_{1}c_{2}-a_{2}c_{1},a_{1}b_{2}-a_{2}b_{1}\rangle t$

对于那些喜欢更简洁表达的人

$L:\langle x_{0},y_{0},0\rangle +\langle b_{1}c_{2}-b_{2}c_{1},a_{1}c_{2}-a_{2}c_{1},a_{1}b_{2}-a_{2}b_{1}\rangle t$

$L:\mathbf {P_{0}} +(\mathbf {n_{1}} \times \mathbf {n_{2}} )t$

如果要想知道两个平面之间的夹角，类似于我们求两条直线之间的夹角，可以应用点积

$\theta =\arccos({\frac {\mathbf {n_{1}} \,\cdot \,\mathbf {n_{2}} }{\|\mathbf {n_{1}} \|\|\mathbf {n_{2}} \|}})$

$\blacksquare$

两个平行平面之间的距离

两个不平行平面之间的距离为零，因为它们相交。所以，我们应该关注平行平面之间的距离。在我们进行之前，如果我们知道点到平面的距离，会更方便。

设距离为 $D$ ，点为 $P=(x_{1},y_{1},z_{1})$ ，平面为 $ax+by+cz+d=0$ .

知道平面的方程可以帮助我们知道法向量，因为法向量垂直于平面，是我们需要的准确方向。 $\mathbf {n} =\langle a,b,c\rangle$ .

现在，我们开始求解。首先，假设存在一个点 $P_{0}=(x_{0},y_{0},z_{0})$ 在平面 $ax+by+cz+d=0$ 上。然后，我们创建一个从 $P_{0}$ 到 $P$ 的向量： ${\overrightarrow {P_{0}P}}=\langle x_{1}-x_{0},y_{1}-y_{0},z_{1}-z_{0}\rangle$ 。我们还将向量 ${\overrightarrow {P_{0}P}}$ 和 $\mathbf {n}$ 之间的夹角设为 $\theta$ 。如果我们绘制出它的图形，我们可以很容易地理解距离是如何推导出来的。

$D=|\|{\overrightarrow {P_{0}P}}\|\ \cos \theta |$ （需要使用绝对值，因为距离应该始终大于零）

然而，我们不知道 $\theta$ 。我们可以通过应用点积来计算 $\theta$ 。但是，有一种更简单的方法。

使用一些非常有趣的运算，我们可以得到
$D={\frac {|\|\mathbf {n} \|\|{\overrightarrow {P_{0}P}}\|\cos \theta |}{\|\mathbf {n} \|}}$
正如我们所见，分子实际上是表达两个向量点积的另一种方式。因此，我们可以不再担心不知道 $\theta$ 的值。
$D={\frac {|\mathbf {n} \ \cdot \ {\overrightarrow {P_{0}P}}|}{\|\mathbf {n} \|}}$
我们现在可以用它们的坐标来替换这些向量。经过一些代数运算，我们得到
$D={\frac {|\mathbf {n} \ \cdot \ {\overrightarrow {P_{0}P}}|}{\|\mathbf {n} \|}}={\frac {|ax_{1}+by_{1}+cz_{1}-(ax_{0}+by_{0}+cz_{0})|}{\sqrt {a^{2}+b^{2}+c^{2}}}}$
由于 $P_{0}=(x_{0},y_{0},z_{0})$ 在平面上， $ax_{0}+by_{0}+cz_{0}=-d$ 。我们可以进一步简化公式为 $D={\frac {|ax_{1}+by_{1}+cz_{1}+d|}{\sqrt {a^{2}+b^{2}+c^{2}}}}$ ，从而完成了我们的推导。

还有其他方法可以写出该公式。对于喜欢更简单符号的人来说，以下公式也是表示距离的方法

$D={\frac {|\mathbf {n} \ \cdot \ {\overrightarrow {P_{0}P}}|}{\|\mathbf {n} \|}}$ 或 $D=\mathrm {comp} _{\mathbf {n} }{\overrightarrow {P_{0}P}}$

$\blacksquare$

经过对距离公式的进一步“研究”，我们可以发现，只需要平面的方程和一个点就可以计算它们之间的距离，这非常方便，因为我们需要解决问题的因素越少，问题就越方便。当我们尝试找到两个平行平面之间的距离时，我们只需要一个平面上的一个点和平面的方程来解决。

两条异面直线之间的距离（续）

假设直线 $L_{1},L_{2}$ 是异面直线，我们可以通过假设这些直线属于两个平行平面 $P_{1},P_{2}$ 来计算距离。然后，问题就从求解两条异面直线之间的距离变为求解两个平行平面之间的距离。

我们仍然需要知道两个平面的法向量。我们可以简单地对两条直线的两个方向向量进行叉积运算： $\mathbf {n} =\mathbf {v_{1}} \times \mathbf {v_{2}}$ 。 $\mathbf {n} \neq 0$ 因为 $\mathbf {v_{1}} ,\mathbf {v_{2}}$ 并不指向相同的方向。现在我们可以将新推导出的距离公式应用于两条异面直线。

圆柱体和二次曲面

本章节需要您对圆锥曲线有一定的了解（参见第1.6章）。

圆柱

圆柱面是由所有平行于一条给定直线并穿过给定平面曲线的直线组成的曲面。存在几种特殊的圆柱面，例如抛物柱面和圆柱面。例如，右侧的图像是抛物柱面。抛物柱面通常具有以下方程

$z=x^{2}$ 等。

如果我们想在不旋转的情况下移动圆柱体，我们可以有以下方程

$z-k=(x-h)^{2}$ ，其中 $h,k$ 是常数。

这与我们在第1.6章早期讨论过的抛物线类似，但增加了一个新的维度。圆柱面，类似于我们推导出抛物柱面的方式，看起来就像一个圆柱体，其“底面”是圆形，方程为

$x^{2}+y^{2}=1$ 等。

如果我们想使圆柱面更“椭圆形”，就像我们推导出椭圆方程的方式一样，椭圆柱面具有以下方程

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$ ，其中 $a,b$ 是常数。

这就像 $xy$ 平面上的一个椭圆，但在 $z$ 方向上无限延伸。

二次曲面

二次曲面的通用方程

二次曲面的通用方程为

Ax^{2}+By^{2}+Cz^{2}+Dxy+Eyz+Fxz+Gx+Hy+Iz+J=0

其中 $A,B,C,D,E,F,G,H,I,J$ 是常数。

它看起来类似于圆锥曲线的通用方程（ $Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$ ），除了它还有一个变量 $z$ 。经过一些平移和旋转，我们可以将通用方程简化为标准方程

二次曲面的标准方程

二次曲面的标准方程为

Ax^{2}+By^{2}+Cz^{2}+J=0\quad {\text{or}}\quad Ax^{2}+By^{2}+Iz=0

其中 $A,B,C,I,J$ 是常数。

当然，根据具体的二次曲面，存在不同的标准方程形式，我们将在接下来的讨论中看到。

椭球面

椭球的方程为

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}+{\frac {z^{2}}{c^{2}}}=1$

绘制二次曲面比较困难，因为不像二维平面那样只有两个变量，而是有三个变量，如果没有计算器的帮助，绘制过程会非常复杂。但是，有一种方法可以让我们更容易理解。我们可以分析每个平面上的形状，然后将每个平面上的分析结果组合起来，形成一个相当完整的曲面图。以这个为例

$x^{2}+{\frac {y^{2}}{9}}+{\frac {z^{2}}{4}}=1$

首先让我们检查 $xy$ -平面。为了检查 $xy$ -平面，我们需要想象 $z$ 为一个常数。在这种情况下，假设 $z=k$ ，那么

$x^{2}+{\frac {y^{2}}{9}}=1-{\frac {k^{2}}{4}}$ ，其中 $-2\leq k\leq 2$ 。

我们可以看到，在 $xy$ -平面上，图形将像一个椭圆。我们称之为在平面 $z=k$ 上的水平截面为椭圆。

让我们进一步分析在平面 $x=k,y=k$ 上的垂直截面。

${\frac {y^{2}}{9}}+{\frac {z^{2}}{4}}=1-k^{2}\quad x=k$ ，其中 $-1\leq k\leq 1$ 。

$x^{2}+{\frac {z^{2}}{4}}=1-{\frac {k^{2}}{9}}\quad y=k$ ，其中 $-3\leq k\leq 3$ 。

我们可以看到，在平面 $x=k,y=k$ 上的两个垂直截面上都是椭圆。换句话说，在 $xz$ 平面和 $yz$ 平面上，图形看起来像椭圆。由于所有截面都是椭圆，所以该曲面是一个椭球，顶点为 $(\pm 1,0,0),(0,\pm 3,0),(0,0,\pm 2)$ 。

椭圆抛物面

椭圆抛物面的方程为

${\frac {z}{c}}={\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}$

根据哪个截面是椭圆，方程会有所不同。对于上面的方程，水平截面是椭圆，如右图所示。

例如，取 $z=x^{2}+y^{2}$ ，水平截面，即 $z=k$ 为

$x^{2}+y^{2}=k$ ，其中 $k>0$ 。

对于两个垂直截面，我们可以看到它们都是抛物线形状。

$z=x^{2}+k^{2}\quad y=k$

$z=y^{2}+k^{2}\quad x=k$

该椭圆抛物面的顶点为 $(0,0,0)$ 。

双曲抛物面

双曲抛物面的方程为

${\frac {z}{c}}={\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}$

相应的截面是

${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}={\frac {k}{c}}\quad z=k$ ，其中 ${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}={\frac {k}{c}}{\text{ when }}k>0\quad {\text{and}}\quad {\frac {y^{2}}{b^{2}}}-{\frac {x^{2}}{a^{2}}}={\frac {k}{c}}{\text{ when }}k<0$ 。水平截面是双曲线。

${\frac {z}{c}}={\frac {x^{2}}{a^{2}}}-{\frac {k^{2}}{b^{2}}}\quad y=k$ 。垂直截面是抛物线。

${\frac {z}{c}}={\frac {k^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}\quad x=k$ 。垂直截面是抛物线。