通常,你会遇到以显式形式表达的函数,即  的形式。要找到
的形式。要找到  相对于
相对于  的导数,你对等式两边求导,得到
的导数,你对等式两边求导,得到
![{\displaystyle {\frac {dy}{dx}}={\frac {d}{dx}}[f(x)]=f'(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5326dab9b69c29a51068061c1f34ceabf1ac8a03)
但假设你有一个  的关系。在这种情况下,将
的关系。在这种情况下,将  解为
解为  的函数可能不方便,甚至不可能。一个很好的例子是关系
的函数可能不方便,甚至不可能。一个很好的例子是关系  。在这种情况下,你可以利用 **隐函数求导** 来求导数。为此,对等式两边求导,并解出
。在这种情况下,你可以利用 **隐函数求导** 来求导数。为此,对等式两边求导,并解出  。也就是说,形成
。也就是说,形成
![{\displaystyle {\frac {d}{dx}}{\bigl [}f{\bigl (}x,y(x){\bigr )}{\bigr ]}={\frac {d}{dx}}{\big [}g{\bigl (}x,y(x){\bigr )}{\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6016d795e7556324ef64947c8f84f10be41ffea6)
并解出  。每当你对一个变量相对于另一个变量求导时,都需要使用链式法则。例如,
。每当你对一个变量相对于另一个变量求导时,都需要使用链式法则。例如,
![{\displaystyle {\frac {d}{dx}}(y^{3})={\frac {d}{dy}}[y^{3}]\cdot {\frac {dy}{dx}}=3y^{2}\cdot y'}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5d3b59fad82ccce72ecf27b8e1675128c39404d)
要理解隐函数微分法并有效地使用它,重要的是要认识到其核心思想就是链式法则。首先让我们回顾一下链式法则。假设我们有两个可微函数  ,我们想知道函数
,我们想知道函数  的导数,链式法则指出
的导数,链式法则指出
![{\displaystyle {\frac {d}{dx}}{\bigl [}f{\bigl (}g(x){\bigr )}{\bigr ]}=f'{\bigl (}g(x){\bigr )}\cdot g'(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e596118af0cab829b12dec0a6f0ee05d4f242694)
也就是说,我们先对  进行正常的求导,然后代入
进行正常的求导,然后代入  ,最后将结果乘以
,最后将结果乘以  的导数。
的导数。
现在假设我们要对像  这样的项求导,相对于
这样的项求导,相对于  ,我们认为
,我们认为  是
是  的函数,所以在接下来的计算中,我们将其写成
的函数,所以在接下来的计算中,我们将其写成  ,而不是仅仅写成
,而不是仅仅写成  。项
。项  只是
只是  和
和  的复合函数。也就是说,
的复合函数。也就是说, 。回想一下
。回想一下  ,那么链式法则指出
,那么链式法则指出
![{\displaystyle {\frac {d}{dx}}{\bigl [}f{\bigl (}y(x){\bigr )}{\bigr ]}=f'{\bigl (}y(x){\bigr )}\cdot y'(x)=2y(x)y'(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57a24127aed120ea4e263f431119c0502cf494e4)
当然,我们通常认为  是
是  的函数,而并非总是写成
的函数,而并非总是写成  ,所以这个计算通常简写为
,所以这个计算通常简写为

不要因为我们还不知道  是什么而感到困惑,它只是一个函数,而且经常地,如果我们对两个相等的量求导,那么就可以显式地解出
是什么而感到困惑,它只是一个函数,而且经常地,如果我们对两个相等的量求导,那么就可以显式地解出  (正如我们将在下面的例子中看到的)。这使得它成为求导的一种非常强大的技术。
(正如我们将在下面的例子中看到的)。这使得它成为求导的一种非常强大的技术。
例如,假设我们对 相对于
相对于  的导数感兴趣,其中
的导数感兴趣,其中  由以下等式关联
由以下等式关联

此等式表示一个以原点为中心,半径为 1 的圆。请注意  不是
不是  的函数,因为它不满足 垂直线测试(例如,当
的函数,因为它不满足 垂直线测试(例如,当  时,
时, )。
)。
为了找到  ,首先我们可以分离变量得到
,首先我们可以分离变量得到

两边开平方,我们得到  的两个独立函数
的两个独立函数

我们可以将其改写为分数幂

使用链式法则,我们得到

简化并代入  到这个方程中,我们得到
到这个方程中,我们得到

使用相同的方程

首先,对等式两边求导 
![{\displaystyle {\frac {d}{dx}}[x^{2}+y^{2}]={\frac {d}{dx}}[1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00d1e61ce2b704b39884bf0912548093b9241785)
![{\displaystyle {\frac {d}{dx}}[x^{2}]+{\frac {d}{dx}}[y^{2}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/312afa8f5fb0007e43ed0d3a892552c4a7b9c56d)
为了对等式左侧的第二项(称为  )求导,使用链式法则
)求导,使用链式法则

所以等式变为

分离变量

将等式两边除以  ,并简化得到与上面相同的结论
,并简化得到与上面相同的结论


当求导无法显式求导的方程时,隐式求导非常有用,因为无法分离变量。
例如,考虑方程:

对等式两边求导(记住对项  使用乘积法则)
使用乘积法则)

将包含  的项分离
的项分离

提取公因子  并将等式两边除以另一项
并将等式两边除以另一项


可以解为

然后求导

然而,使用隐函数求导也可以像这样求导
![{\displaystyle {\frac {d}{dx}}[xy]={\frac {d}{dx}}[1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b616e67fbda614eaacc9c29cbcbe0abbbe377a63)
使用乘积法则

解出 

注意,如果我们将  代入
代入  ,我们最终得到
,我们最终得到  。
。
反正弦、反余弦、反正切。这些函数允许你根据某个角度的正弦、余弦或正切来确定该角度。
首先,让我们从反正弦开始,使得

为了找到  ,我们首先需要将其分解成我们可以处理的形式
,我们首先需要将其分解成我们可以处理的形式

然后我们可以对它求导

…并解出 
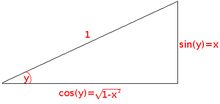
 给我们这个单位三角形。
给我们这个单位三角形。

在这一点上,我们需要回到单位三角形。由于  是角度,对边是
是角度,对边是  ,邻边是
,邻边是  ,斜边是 1。由于我们已经根据单位三角形确定了
,斜边是 1。由于我们已经根据单位三角形确定了  的值,我们可以将其代入上面的方程,得到
的值,我们可以将其代入上面的方程,得到
反正弦函数的导数

|
我们可以对反余弦函数和反正切函数使用相同的方法
反余弦函数的导数

|
反正切函数的导数

|





![{\displaystyle {\frac {dy}{dx}}={\frac {d}{dx}}[f(x)]=f'(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5326dab9b69c29a51068061c1f34ceabf1ac8a03)



![{\displaystyle {\frac {d}{dx}}{\bigl [}f{\bigl (}x,y(x){\bigr )}{\bigr ]}={\frac {d}{dx}}{\big [}g{\bigl (}x,y(x){\bigr )}{\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6016d795e7556324ef64947c8f84f10be41ffea6)

![{\displaystyle {\frac {d}{dx}}(y^{3})={\frac {d}{dy}}[y^{3}]\cdot {\frac {dy}{dx}}=3y^{2}\cdot y'}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5d3b59fad82ccce72ecf27b8e1675128c39404d)


![{\displaystyle {\frac {d}{dx}}{\bigl [}f{\bigl (}g(x){\bigr )}{\bigr ]}=f'{\bigl (}g(x){\bigr )}\cdot g'(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e596118af0cab829b12dec0a6f0ee05d4f242694)







![{\displaystyle {\frac {d}{dx}}{\bigl [}f{\bigl (}y(x){\bigr )}{\bigr ]}=f'{\bigl (}y(x){\bigr )}\cdot y'(x)=2y(x)y'(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57a24127aed120ea4e263f431119c0502cf494e4)










![{\displaystyle {\frac {d}{dx}}[x^{2}+y^{2}]={\frac {d}{dx}}[1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00d1e61ce2b704b39884bf0912548093b9241785)
![{\displaystyle {\frac {d}{dx}}[x^{2}]+{\frac {d}{dx}}[y^{2}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/312afa8f5fb0007e43ed0d3a892552c4a7b9c56d)














![{\displaystyle {\frac {d}{dx}}[xy]={\frac {d}{dx}}[1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b616e67fbda614eaacc9c29cbcbe0abbbe377a63)












