通常情况下,你会遇到以显式形式表达的函数,即以  的形式表达。为了求
的形式表达。为了求  关于
关于  的导数,你需要对等式两边求关于
的导数,你需要对等式两边求关于  的导数,得到
的导数,得到
![{\displaystyle {\frac {dy}{dx}}={\frac {d}{dx}}[f(x)]=f'(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5326dab9b69c29a51068061c1f34ceabf1ac8a03)
但假设你有一个形式为  的关系。在这种情况下,将
的关系。在这种情况下,将  表示为
表示为  的函数可能很麻烦,甚至不可能。一个很好的例子是关系式
的函数可能很麻烦,甚至不可能。一个很好的例子是关系式  。在这种情况下,你可以利用 **隐函数微分** 来求导数。为此,你需要对等式两边求关于
。在这种情况下,你可以利用 **隐函数微分** 来求导数。为此,你需要对等式两边求关于  的导数,并求解
的导数,并求解  。也就是说,形成
。也就是说,形成
![{\displaystyle {\frac {d}{dx}}{\bigl [}f{\bigl (}x,y(x){\bigr )}{\bigr ]}={\frac {d}{dx}}{\big [}g{\bigl (}x,y(x){\bigr )}{\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6016d795e7556324ef64947c8f84f10be41ffea6)
并求解  。每当你对一个变量关于另一个变量求导时,都需要使用链式法则。例如,
。每当你对一个变量关于另一个变量求导时,都需要使用链式法则。例如,
![{\displaystyle {\frac {d}{dx}}(y^{3})={\frac {d}{dy}}[y^{3}]\cdot {\frac {dy}{dx}}=3y^{2}\cdot y'}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5d3b59fad82ccce72ecf27b8e1675128c39404d)
要理解隐函数求导的原理并熟练运用它,必须认识到其关键思想就是链式法则。首先让我们回顾一下链式法则。假设我们有两个可微函数  ,我们感兴趣的是计算函数
,我们感兴趣的是计算函数  的导数,链式法则表明
的导数,链式法则表明
![{\displaystyle {\frac {d}{dx}}{\bigl [}f{\bigl (}g(x){\bigr )}{\bigr ]}=f'{\bigl (}g(x){\bigr )}\cdot g'(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e596118af0cab829b12dec0a6f0ee05d4f242694)
也就是说,我们像正常一样对  求导,然后代入
求导,然后代入  ,最后将结果乘以
,最后将结果乘以  的导数。
的导数。
现在假设我们要对类似  的项进行微分,相对于
的项进行微分,相对于  ,我们认为
,我们认为  是
是  的函数,所以在这个计算的剩余部分,我们将其写成
的函数,所以在这个计算的剩余部分,我们将其写成  而不是仅仅写成
而不是仅仅写成  。
。  只是
只是  和
和  的复合函数。也就是说,
的复合函数。也就是说,  。 回想一下
。 回想一下  ,那么链式法则指出
,那么链式法则指出
![{\displaystyle {\frac {d}{dx}}{\bigl [}f{\bigl (}y(x){\bigr )}{\bigr ]}=f'{\bigl (}y(x){\bigr )}\cdot y'(x)=2y(x)y'(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57a24127aed120ea4e263f4311119c0502cf494e4)
当然,通常我们认为  是
是  的函数,而不必总是写成
的函数,而不必总是写成  ,所以这个计算通常只写成
,所以这个计算通常只写成

不要被我们还不知道  是什么这个事实所迷惑,它是一个函数,而且通常如果我们对两个相等的量求导,就可以显式地解出
是什么这个事实所迷惑,它是一个函数,而且通常如果我们对两个相等的量求导,就可以显式地解出  (正如我们将在下面的例子中看到的)。这使得它成为求导数的一种非常强大的技术。
(正如我们将在下面的例子中看到的)。这使得它成为求导数的一种非常强大的技术。
例如,假设我们对  相对于
相对于  的导数感兴趣,其中
的导数感兴趣,其中  由以下方程相关联
由以下方程相关联

这个方程表示一个以原点为中心的半径为 1 的圆。请注意, 不是
不是  的函数,因为它不满足 垂直线测试 (
的函数,因为它不满足 垂直线测试 ( 当
当  时,例如)。
时,例如)。
要找到  ,首先我们可以分离变量得到
,首先我们可以分离变量得到

对等式两边开平方根,我们得到两个关于  的独立函数
的独立函数

我们可以将其改写为分数幂

利用链式法则,我们得到:

并通过将  代回这个方程进行简化,得到
代回这个方程进行简化,得到

使用相同的方程

首先,对等式两边关于  求导
求导
![{\displaystyle {\frac {d}{dx}}[x^{2}+y^{2}]={\frac {d}{dx}}[1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00d1e61ce2b704b39884bf0912548093b9241785)
![{\displaystyle {\frac {d}{dx}}[x^{2}]+{\frac {d}{dx}}[y^{2}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/312afa8f5fb0007e43ed0d3a892552c4a7b9c56d)
为了对等式左边第二项(记为  )进行求导,可以使用链式法则
)进行求导,可以使用链式法则

因此,该方程变为

分离变量

两边同除以  ,并简化得到与上面相同的解
,并简化得到与上面相同的解


当对无法显式求导的方程进行求导时,隐式求导非常有用,因为无法将变量分离。
例如,考虑方程

对等式两边进行求导(记住对项  使用乘积法则)
使用乘积法则)

将包含  的项分离出来
的项分离出来

提取公因子  ,并将两边除以另一项
,并将两边除以另一项


可以解为

然后求导

然而,使用隐式微分,也可以这样进行微分
![{\displaystyle {\frac {d}{dx}}[xy]={\frac {d}{dx}}[1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b616e67fbda614eaacc9c29cbcbe0abbbe377a63)
使用乘积法则

解出 

注意,如果我们将  代入
代入  ,我们将再次得到
,我们将再次得到  。
。
反正弦、反余弦、反正切。这些函数允许你根据一个角的正弦、余弦或正切来确定这个角。
首先,我们从反正弦开始,使得

为了找到  ,我们需要首先把它分解成我们可以处理的形式
,我们需要首先把它分解成我们可以处理的形式

然后我们可以对它求导

…并解出 
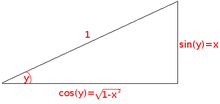
 给我们这个单位三角形。
给我们这个单位三角形。

此时,我们需要回到单位圆三角形。由于  是角,而对边是
是角,而对边是  ,邻边是
,邻边是  ,斜边是 1。 由于我们已经根据单位圆三角形确定了
,斜边是 1。 由于我们已经根据单位圆三角形确定了  的值,我们可以将其代回上面的方程,得到
的值,我们可以将其代回上面的方程,得到
反正弦函数的导数

|
我们可以对反余弦和反正切函数使用相同的步骤
反余弦函数的导数

|
反正切函数的导数

|





![{\displaystyle {\frac {dy}{dx}}={\frac {d}{dx}}[f(x)]=f'(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5326dab9b69c29a51068061c1f34ceabf1ac8a03)



![{\displaystyle {\frac {d}{dx}}{\bigl [}f{\bigl (}x,y(x){\bigr )}{\bigr ]}={\frac {d}{dx}}{\big [}g{\bigl (}x,y(x){\bigr )}{\big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6016d795e7556324ef64947c8f84f10be41ffea6)

![{\displaystyle {\frac {d}{dx}}(y^{3})={\frac {d}{dy}}[y^{3}]\cdot {\frac {dy}{dx}}=3y^{2}\cdot y'}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5d3b59fad82ccce72ecf27b8e1675128c39404d)


![{\displaystyle {\frac {d}{dx}}{\bigl [}f{\bigl (}g(x){\bigr )}{\bigr ]}=f'{\bigl (}g(x){\bigr )}\cdot g'(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e596118af0cab829b12dec0a6f0ee05d4f242694)







![{\displaystyle {\frac {d}{dx}}{\bigl [}f{\bigl (}y(x){\bigr )}{\bigr ]}=f'{\bigl (}y(x){\bigr )}\cdot y'(x)=2y(x)y'(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57a24127aed120ea4e263f4311119c0502cf494e4)










![{\displaystyle {\frac {d}{dx}}[x^{2}+y^{2}]={\frac {d}{dx}}[1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00d1e61ce2b704b39884bf0912548093b9241785)
![{\displaystyle {\frac {d}{dx}}[x^{2}]+{\frac {d}{dx}}[y^{2}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/312afa8f5fb0007e43ed0d3a892552c4a7b9c56d)














![{\displaystyle {\frac {d}{dx}}[xy]={\frac {d}{dx}}[1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b616e67fbda614eaacc9c29cbcbe0abbbe377a63)












