平面的坐标

类型

一般类型

线性/非线性（轴的刻度）
维度：1D、2D、3D、...
3D 的方向
- 手性（右手坐标系 (RHS) 或左手坐标系 (LHS))^[1]
原点位置
- 左上角原点坐标系（原点位于屏幕的左上角，x 和 y 向右和向下为正）
- 左下角原点坐标系（原点位于窗口或客户端区域的左下角）
- 中间 = 中心原点坐标系（0,0 坐标位于中间。x 从左到右增加。y 从下到上增加。）

存在不同的二维坐标系：^[2]

笛卡尔坐标系（直角、正交）
椭圆坐标系（曲线坐标）
抛物线
极坐标
对数极坐标
双极坐标
规范化齐次坐标

计算机图形中的类型

世界坐标（使用浮点数）^[3]
设备坐标^[4]
- 屏幕坐标（使用整数）用于屏幕、位图或数组的像素

这两种类型之间的关系创建了新项目

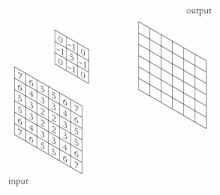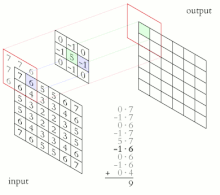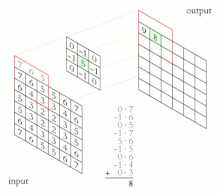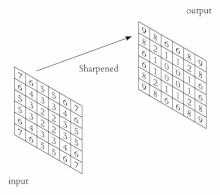
像素^[5] 大小（像素间距）与缩放有关
屏幕和整数坐标之间的映射（转换）^[6]^[7]
裁剪
光栅化

这些不是

地理空间坐标
- 地理坐标系 (GCS)
- 空间参考系统 (SRS) 或坐标参考系统 (CRS)

笛卡尔坐标系

笛卡尔坐标系用于欧几里得几何。

裁剪
窗口-视口变换

笛卡尔坐标系

1D、2D、3D、...
每个轴上的线性刻度（保持形状）
坐标
- 正交（直角）
- 极坐标

元素

原点 (0,0) 及其位置
单位
方向
宽度、高度

齐次坐标

齐次坐标或射影坐标，由奥古斯特·费迪南德·莫比乌斯于 1827 年引入，是射影几何中使用的一种坐标系。

它们具有以下优点：

可以使用有限坐标表示包括无穷远点在内的点的坐标
涉及齐次坐标的公式通常比它们的笛卡尔对应公式更简单、更对称
齐次坐标具有广泛的应用，包括计算机图形和三维计算机视觉，它们允许仿射变换以及一般来说射影变换很容易用矩阵表示
使用规范化的齐次坐标避免了有理函数迭代中的溢出和下溢错误迭代

在齐次坐标中，二维平面上的一个点是一个三元组（一个由 3 个数字组成的有限有序列表（序列））^[8]: $x,y,w$

元素

扩展的欧几里得平面或实射影平面

转换

从齐次坐标 $(x,y,w)$ 到笛卡尔坐标 $(x,y)$ 的转换，我们只需将每个笛卡尔坐标 $x$ 和 $y$ 除以 $w$ ^[9]

 $({\frac {x}{w}},{\frac {y}{w}})$

要将笛卡尔坐标 $(x,y)$ 转换为齐次坐标，在末尾添加一个第三个坐标 1

 $(x,y,1)$

齐次坐标下的矩阵运算

对数极坐标

在数学中，对数极坐标（或对数极坐标）是二维坐标系，其中点由两个数字标识

一个表示到某个点的距离的对数
一个表示角度

对数极坐标与极坐标密切相关，极坐标通常用于描述具有某种旋转对称性的平面域。在诸如调和分析和复分析的领域中，对数极坐标比极坐标更规范。另请参阅指数映射

定义

平面上的对数极坐标由一对实数 (ρ,θ) 组成，其中 ρ 是给定点与原点之间距离的对数，θ 是参考线（x 轴）与过原点和该点的直线之间的角度。角度坐标与极坐标相同，而半径坐标根据以下规则进行变换

r=e^{\rho }

.

其中 $r$ 是到原点的距离。

对数极坐标映射：从笛卡尔空间 (x,y) 到极坐标空间或 (ρ,θ) 空间的近似映射^[10]

 $x,y\to \rho ,\theta \to log(\rho ),\theta$

 $\rho ={\sqrt {(x-x_{c})^{2}+(y-y_{c})^{2}}}$ 
 $\theta ={\frac {y-y_{c}}{x-x_{c}}}$

其中

其中 $\rho$ 是图像中心（例如 $(x_{c},y_{c})$ ）的径向距离
$\theta$ 表示角度。

应用

图像分析

早在 1970 年代末，离散螺旋坐标系的应用已出现在图像分析（图像配准）中。用这种坐标系而不是笛卡尔坐标系来表示图像，在旋转或放大图像时具有计算优势。此外，人眼视网膜中的光感受器分布方式与螺旋坐标系非常相似。^[11] 它也可以在曼德勃罗特分形中找到（参见右侧图片）。

对数极坐标还可以用于构建拉东变换及其逆变换的快速方法。^[12]

离散几何

由对数极坐标给出的圆盘中的离散坐标系 (n = 25)
可以很容易地用对数极坐标表示的圆盘中的离散坐标系 (n = 25)
$Part of a Mandelbrot fractal showing spiral behaviour$

显示螺旋行为的曼德勃罗特分形的一部分

为了用数值方法求解一个域中的偏微分方程，必须在这个域中引入一个离散的坐标系。如果这个域具有旋转对称性，并且您想要一个由矩形组成的网格，那么极坐标是一个糟糕的选择，因为它在圆心处会产生三角形而不是矩形。

然而，可以通过以下方式引入对数极坐标来解决这个问题

将平面分成边长为 2 $\pi$ /n 的正方形网格，其中 n 是一个正整数
使用复指数函数在平面上创建对数极坐标网格。然后，左半平面被映射到单位圆盘上，半径的数量等于 n。更重要的是，可以将这些正方形的对角线映射到单位圆盘上，这将在单位圆盘中产生一个由螺旋线组成的离散坐标系，请参阅右侧的图形。

屏幕或图像或设备坐标

图像中的坐标值始终为正^[13]
原点 = 点 (90, 0) 位于屏幕的左上角
坐标是整数值
屏幕上的坐标系是左手系的，即 x 坐标从左到右增加，y 坐标从上到下增加。

栅格 2D 图形

世界坐标

// from screen to world coordinate ; linear mapping
// uses global cons
double GiveZx (int ix)
{
  return (ZxMin + ix * PixelWidth);
}

// uses globaal cons
double GiveZy (int iy)
{
  return (ZyMax - iy * PixelHeight);
}				// reverse y axis


complex double GiveZ (int ix, int iy)
{
  double Zx = GiveZx (ix);
  double Zy = GiveZy (iy);

  return Zx + Zy * I;




}

  // modified code using center and radius to scan the plane 
  int height = 720;
  int width = 1280;
  double dWidth;
  double dRadius = 1.5;
  double complex center= -0.75*I;
  double complex c;
  int i,j;

  double width2; // = width/2.0
  double height2; // = height/2.0
  
  width2 = width /2.0;
  height2 = height/2.0;

complex double coordinate(int i, int j, int width, int height, complex double center, double radius) {
  double x = (i - width /2.0) / (height/2.0);
  double y = (j - height/2.0) / (height/2.0);
  complex double c = center + radius * (x - I * y);
  return c;
}

for ( j = 0; j < height; ++j) {
    for ( i = 0; i < width; ++i) {
      c = coordinate(i, j, width, height, center, dRadius);
      // do smth 
       }
     }

或者简称为

 
 double pixel_spacing = radius / (height / 2.0);
 complex double c = center + pixel_spacing * (x-width/2.0 + I * (y-height/2.0));

坐标变换

另请参阅

平面变换

通常，存在许多不同的坐标系来描述几何图形。不同系统之间的关系由坐标变换描述，该变换给出了一个系统中的坐标关于另一个系统中的坐标的公式。例如，在平面上，如果笛卡尔坐标 (x, y) 和极坐标 (r, θ) 具有相同的原点，并且极轴是正的 x 轴，则从极坐标到笛卡尔坐标的坐标变换由 x = r cosθ 和 y = r sinθ 给出。

对于空间到自身的每个双射，都可以关联两个坐标变换

使得每个点的像的新坐标与原始点的老坐标相同（映射的公式是坐标变换的逆公式）
使得每个点的像的老坐标与原始点的新坐标相同（映射的公式与坐标变换的公式相同）

例如，在 1D 中，如果映射是向右平移 3，则第一个将原点从 0 移动到 3，使得每个点的坐标减少 3，而第二个将原点从 0 移动到 -3，使得每个点的坐标增加 3。以下是使用最广泛的一些坐标变换的列表。

二维

设 (x, y) 为标准笛卡尔坐标，(r, θ) 为标准极坐标。

到笛卡尔坐标

从极坐标

{\begin{aligned}x&=r\cos \theta \\y&=r\sin \theta \\[5pt]{\frac {\partial (x,y)}{\partial (r,\theta )}}&={\begin{bmatrix}\cos \theta &-r\sin \theta \\\sin \theta &r\cos \theta \end{bmatrix}}\\[5pt]{\text{Jacobian}}=\det {\frac {\partial (x,y)}{\partial (r,\theta )}}&=r\end{aligned}}

从对数极坐标

从笛卡尔坐标到对数极坐标的变换公式由下式给出

{\begin{cases}\rho =\ln \left({\sqrt {x^{2}+y^{2}}}\right),\\\theta =\operatorname {atan2} (y,\,x).\end{cases}}

从对数极坐标到笛卡尔坐标的变换公式为

{\begin{cases}x=e^{\rho }\cos \theta ,\\y=e^{\rho }\sin \theta .\end{cases}}

使用复数 (x, y) = x + iy，后一种变换可以写成

x+iy=e^{\rho +i\theta }

即复指数函数。

由此可以得出，谐波分析和复分析中的基本方程将与笛卡尔坐标系中的形式相同。这在极坐标系中是不成立的。

{\begin{aligned}x&=e^{\rho }\cos \theta ,\\y&=e^{\rho }\sin \theta .\end{aligned}}

使用复数 $(x,y)=x+iy'$ ，变换可以写成

x+iy=e^{\rho +i\theta }

也就是说，它是用复指数函数给出的。

从双极坐标

{\begin{aligned}x&=a{\frac {\sinh \tau }{\cosh \tau -\cos \sigma }}\\y&=a{\frac {\sin \sigma }{\cosh \tau -\cos \sigma }}\end{aligned}}

从双心双极坐标

{\begin{aligned}x&={\frac {1}{4c}}\left(r_{1}^{2}-r_{2}^{2}\right)\\y&=\pm {\frac {1}{4c}}{\sqrt {16c^{2}r_{1}^{2}-(r_{1}^{2}-r_{2}^{2}+4c^{2})^{2}}}\end{aligned}}

从切萨罗方程

{\begin{aligned}x&=\int \cos \left[\int \kappa (s)\,ds\right]ds\\y&=\int \sin \left[\int \kappa (s)\,ds\right]ds\end{aligned}}

到极坐标

从笛卡尔坐标

{\begin{aligned}r&={\sqrt {x^{2}+y^{2}}}\\\theta '&=\arctan \left|{\frac {y}{x}}\right|\end{aligned}}

注意：求解 $\theta '$ 会得到第一象限的角 ( ${\textstyle 0<\theta <{\frac {\pi }{2}}}$ )。为了找到 $\theta$ ，必须参考原始的笛卡尔坐标，确定 $\theta$ 所在的象限（例如，(3,−3) [笛卡尔坐标] 位于第四象限），然后使用以下方法求解 $\theta$

对于 $\theta '$ 在第一象限
$\theta =\theta '$
对于 $\theta '$ 在第二象限
$\theta =\pi -\theta '$
对于 $\theta '$ 在第三象限
$\theta =\pi +\theta '$
对于 $\theta '$ 在第四象限
$\theta =2\pi -\theta '$

必须用这种方式求解 $\theta$ ，因为对于所有 $\theta$ 的值， $\tan \theta$ 仅在 ${\textstyle -{\frac {\pi }{2}}<\theta <+{\frac {\pi }{2}}}$ 上定义，并且是周期性的（周期为 $\pi$ ）。这意味着反函数将只给出函数域中的值，但限制在一个周期内。因此，反函数的范围只是一个完整圆形的一半。

注意，也可以使用

{\begin{aligned}r&={\sqrt {x^{2}+y^{2}}}\\\theta '&=2\arctan {\frac {y}{x+r}}\end{aligned}}

从双心双极坐标

{\begin{aligned}r&={\sqrt {\frac {r_{1}^{2}+r_{2}^{2}-2c^{2}}{2}}}\\\theta &=\arctan \left[{\sqrt {{\frac {8c^{2}(r_{1}^{2}+r_{2}^{2}-2c^{2})}{r_{1}^{2}-r_{2}^{2}}}-1}}\right]\end{aligned}}

其中，2c 表示两极之间的距离。

从笛卡尔坐标系转换为对数极坐标系

{\begin{aligned}\rho &=\log {\sqrt {x^{2}+y^{2}}},\\\theta &=\arctan {\frac {y}{x}}.\end{aligned}}

弧长和曲率

在笛卡尔坐标系中

{\begin{aligned}\kappa &={\frac {x'y''-y'x''}{({x'}^{2}+{y'}^{2})^{\frac {3}{2}}}}\\s&=\int _{a}^{t}{\sqrt {{x'}^{2}+{y'}^{2}}}\,dt\end{aligned}}

在极坐标系中

{\begin{aligned}\kappa &={\frac {r^{2}+2{r'}^{2}-rr''}{(r^{2}+{r'}^{2})^{\frac {3}{2}}}}\\s&=\int _{a}^{\varphi }{\sqrt {r^{2}+{r'}^{2}}}\,d\varphi \end{aligned}}

三维

设 (x, y, z) 为标准笛卡尔坐标，(ρ, θ, φ) 为球面坐标，其中 θ 为从 +Z 轴测量的角度（如 [1]，参见球面坐标中的约定）。由于 φ 的范围为 360°，因此在取 φ 的反正切时，与极坐标（二维）坐标系中的情况相同。θ 的范围为 180°，从 0° 到 180°，在从反余弦计算时不会出现任何问题，但在取反正切时要小心。

如果在另一种定义中，选择 θ 从 −90° 到 +90°，与先前定义的方向相反，则可以从反正弦唯一地找到它，但要小心反余切。在这种情况下，下面所有公式中 θ 中的所有参数都应该交换正弦和余弦，并且作为导数也应该交换加号和减号。

所有除以零的结果都是沿一个主轴方向的特殊情况，实际上最容易通过观察解决。

到笛卡尔坐标

从球面坐标

{\begin{aligned}x&=\rho \,\sin \theta \,\cos \varphi \\y&=\rho \,\sin \theta \,\sin \varphi \\z&=\rho \,\cos \theta \\{\frac {\partial (x,y,z)}{\partial (\rho ,\theta ,\varphi )}}&={\begin{pmatrix}\sin \theta \cos \varphi &\rho \cos \theta \cos \varphi &-\rho \sin \theta \sin \varphi \\\sin \theta \sin \varphi &\rho \cos \theta \sin \varphi &\rho \sin \theta \cos \varphi \\\cos \theta &-\rho \sin \theta &0\end{pmatrix}}\end{aligned}}

因此体积元

dx\;dy\;dz=\det {\frac {\partial (x,y,z)}{\partial (\rho ,\theta ,\varphi )}}d\rho \;d\theta \;d\varphi =\rho ^{2}\sin \theta \;d\rho \;d\theta \;d\varphi

从圆柱坐标

{\begin{aligned}x&=r\,\cos \theta \\y&=r\,\sin \theta \\z&=z\,\\{\frac {\partial (x,y,z)}{\partial (r,\theta ,z)}}&={\begin{pmatrix}\cos \theta &-r\sin \theta &0\\\sin \theta &r\cos \theta &0\\0&0&1\end{pmatrix}}\end{aligned}}

因此体积元

dV=dx\;dy\;dz=\det {\frac {\partial (x,y,z)}{\partial (r,\theta ,z)}}dr\;d\theta \;dz=r\;dr\;d\theta \;dz

到球面坐标

从笛卡尔坐标

{\begin{aligned}\rho &={\sqrt {x^{2}+y^{2}+z^{2}}}\\\theta &=\arctan \left({\frac {\sqrt {x^{2}+y^{2}}}{z}}\right)=\arccos \left({\frac {z}{\sqrt {x^{2}+y^{2}+z^{2}}}}\right)\\\varphi &=\arctan \left({\frac {y}{x}}\right)=\arccos \left({\frac {x}{\sqrt {x^{2}+y^{2}}}}\right)=\arcsin \left({\frac {y}{\sqrt {x^{2}+y^{2}}}}\right)\\{\frac {\partial \left(\rho ,\theta ,\varphi \right)}{\partial \left(x,y,z\right)}}&={\begin{pmatrix}{\frac {x}{\rho }}&{\frac {y}{\rho }}&{\frac {z}{\rho }}\\{\frac {xz}{\rho ^{2}{\sqrt {x^{2}+y^{2}}}}}&{\frac {yz}{\rho ^{2}{\sqrt {x^{2}+y^{2}}}}}&-{\frac {\sqrt {x^{2}+y^{2}}}{\rho ^{2}}}\\{\frac {-y}{x^{2}+y^{2}}}&{\frac {x}{x^{2}+y^{2}}}&0\\\end{pmatrix}}\end{aligned}}

另请参阅有关atan2的文章，了解如何优雅地处理一些边缘情况。

因此对于元素

d\rho \ d\theta \ d\varphi =\det {\frac {\partial (\rho ,\theta ,\varphi )}{\partial (x,y,z)}}dx\ dy\ dz={\frac {1}{{\sqrt {x^{2}+y^{2}}}{\sqrt {x^{2}+y^{2}+z^{2}}}}}dx\ dy\ dz

从圆柱坐标

{\begin{aligned}\rho &={\sqrt {r^{2}+h^{2}}}\\\theta &=\arctan {\frac {r}{h}}\\\varphi &=\varphi \\{\frac {\partial (\rho ,\theta ,\varphi )}{\partial (r,h,\varphi )}}&={\begin{pmatrix}{\frac {r}{\sqrt {r^{2}+h^{2}}}}&{\frac {h}{\sqrt {r^{2}+h^{2}}}}&0\\{\frac {h}{r^{2}+h^{2}}}&{\frac {-r}{r^{2}+h^{2}}}&0\\0&0&1\\\end{pmatrix}}\\\det {\frac {\partial (\rho ,\theta ,\varphi )}{\partial (r,h,\varphi )}}&={\frac {1}{\sqrt {r^{2}+h^{2}}}}\end{aligned}}

转换为柱坐标

从笛卡尔坐标

{\begin{aligned}r&={\sqrt {x^{2}+y^{2}}}\\\theta &=\arctan {\left({\frac {y}{x}}\right)}\\z&=z\quad \end{aligned}}

{\frac {\partial (r,\theta ,h)}{\partial (x,y,z)}}={\begin{pmatrix}{\frac {x}{\sqrt {x^{2}+y^{2}}}}&{\frac {y}{\sqrt {x^{2}+y^{2}}}}&0\\{\frac {-y}{x^{2}+y^{2}}}&{\frac {x}{x^{2}+y^{2}}}&0\\0&0&1\end{pmatrix}}

从球面坐标

{\begin{aligned}r&=\rho \sin \varphi \\h&=\rho \cos \varphi \\\theta &=\theta \\{\frac {\partial (r,h,\theta )}{\partial (\rho ,\varphi ,\theta )}}&={\begin{pmatrix}\sin \varphi &\rho \cos \varphi &0\\\cos \varphi &-\rho \sin \varphi &0\\0&0&1\\\end{pmatrix}}\\\det {\frac {\partial (r,h,\theta )}{\partial (\rho ,\varphi ,\theta )}}&=-\rho \end{aligned}}

从笛卡尔坐标系获取弧长、曲率和挠率

{\begin{aligned}s&=\int _{0}^{t}{\sqrt {{x'}^{2}+{y'}^{2}+{z'}^{2}}}\,dt\\[3pt]\kappa &={\frac {\sqrt {(z''y'-y''z')^{2}+(x''z'-z''x')^{2}+(y''x'-x''y')^{2}}}{({x'}^{2}+{y'}^{2}+{z'}^{2})^{\frac {3}{2}}}}\\[3pt]\tau &={\frac {x'''(y'z''-y''z')+y'''(x''z'-x'z'')+z'''(x'y''-x''y')}{{(x'y''-x''y')}^{2}+{(x''z'-x'z'')}^{2}+{(y'z''-y''z')}^{2}}}\end{aligned}}

实现

wgpu

wgpu 使用 D3D 和 Metal 的坐标系：^[14]

渲染：中心点为 0，半径为 1，所以右上角为 (1,1)，左下角为 (-1,-1)
纹理：0 为左上角点，右上角为 (1,0)，左下角为 (0,1)

HTML 的 CSS 盒模型

用户坐标系
局部坐标系
变换矩阵

HTML 画布的坐标系 ^[15]

是一个二维网格
x 从左到右增加：从 x=0 (最左边) 到 x=+960 (最右边)
y 从下到上递减：从 y=+720 (底部) 到 y=0 (顶部).
原点 = 0,0 坐标位于左上角 (画布的左上角)

OpenGL

图形管道的三个基本步骤
OpenGL 管道
图形管道中的几何步骤
3D 图形渲染管道

OpenGL 中的五个不同的坐标系：^[16]

局部或对象
世界
视图或眼睛
剪切
屏幕

OpenGl

"OpenGL 在对象空间和世界空间中是右手坐标系，但在窗口空间 (又称屏幕空间) 中，我们突然变成了左手坐标系"^[17]
变换管道：局部坐标 -> 世界坐标 -> 视图坐标 -> 剪切坐标 -> 屏幕坐标^[18] "每个坐标系都为一个或多个 OpenGL 功能服务"^[19]
使用
- 齐次坐标^[20]
- 归一化设备坐标 (NDC) 仅坐标 (x,y,z) : -1 ≤ x,y,z ≤ +1。任何超出此范围的坐标都将被丢弃或剪切 = 不会在屏幕上显示^[21]
- 矩阵微积分

OpenCV

OpenCV 图像坐标系的原点位于图像的左上角

SVG

SVG 坐标系

SVG 中的默认坐标系与 HTML 中的坐标系基本相同
画布是所有 SVG 元素绘制的空间或区域^[22]
视窗定义了一个绘制区域，该区域以大小 (宽度、高度) 和原点为特征，以抽象用户单位测量。术语 SVG 视窗不同于 CSS 中使用的“视窗”术语
视窗^[23]

p5.js 库

二维坐标系^[24]

画布
原点 ( 0,0) 的位置

另请参阅

二维平面变换

参考资料

↑ 约翰·T·贝尔博士的坐标系
↑ 维基百科：坐标系
↑ 计算机图形学 StackExchange 问题：世界坐标、观察坐标和设备坐标之间的区别是什么
↑ Javatpoint：计算机图形学窗口
↑ 像素不是一个小方块，由 Alvy Ray Smith 撰写
↑ 如何将世界坐标转换为屏幕坐标，反之亦然
↑ 如何在 OpenGL 中将二维世界坐标转换为屏幕坐标
↑ 文字和按钮在线 - 一系列交互式内容的齐次坐标交互式指南
↑ 齐次坐标，由 Yasen Hu 撰写
↑ 使用对数极坐标变换和相位相关来恢复更高尺度的图像配准，JIGNESH NATVARLAL SARVAIYA、Suprava Patnaik 博士、Kajal Kothari，JPRR 第 7 卷，第 1 期（2012 年）；doi:10.13176/11.355
↑ Weiman、Chaikin，《用于图像处理和显示的对数螺旋网格》，《计算机图形学和图像处理》第 11 卷，第 197-226 页（1979 年）。
↑ Andersson、Fredrik，《使用对数极坐标和部分反投影对 Radon 变换进行快速反演》，《SIAM 应用数学杂志》第 65 卷，第 818-837 页（2005 年）。
↑ ronny restrepo：点云坐标
↑ raphlinus：wgpu
↑ w3schools：画布坐标
↑ learnopengl：坐标系
↑ stackoverflow 问题：OpenGL 坐标系是左手系还是右手系
↑ learnopengl：坐标系
↑ Paul Martz 撰写的 OpenGL 变换管道
↑ 宋浩安的齐次坐标
↑ ASPOSE 撰写的 SVG 坐标系和单位
↑ Sara Soueidan 撰写的 svg-coordinate-systems
↑ 二维坐标系，伦敦大学金史密斯学院

[1] 约翰·T·贝尔博士的坐标系

[2] 维基百科：坐标系

[3] 计算机图形学 StackExchange 问题：世界坐标、观察坐标和设备坐标之间的区别是什么

[4] Javatpoint：计算机图形学窗口

[5] 像素不是一个小方块，由 Alvy Ray Smith 撰写

[6] 如何将世界坐标转换为屏幕坐标，反之亦然

[7] 如何在 OpenGL 中将二维世界坐标转换为屏幕坐标

[8] 文字和按钮在线 - 一系列交互式内容的齐次坐标交互式指南

[9] 齐次坐标，由 Yasen Hu 撰写

[10] 使用对数极坐标变换和相位相关来恢复更高尺度的图像配准，JIGNESH NATVARLAL SARVAIYA、Suprava Patnaik 博士、Kajal Kothari，JPRR 第 7 卷，第 1 期（2012 年）；doi:10.13176/11.355

[11] Weiman、Chaikin，《用于图像处理和显示的对数螺旋网格》，《计算机图形学和图像处理》第 11 卷，第 197-226 页（1979 年）。

[12] Andersson、Fredrik，《使用对数极坐标和部分反投影对 Radon 变换进行快速反演》，《SIAM 应用数学杂志》第 65 卷，第 818-837 页（2005 年）。

[13] ronny restrepo：点云坐标

[14] raphlinus：wgpu

[15] w3schools：画布坐标

[16] rnopengl：坐标系

[17] stackoverflow 问题：OpenGL 坐标系是左手系还是右手系

[18] rnopengl：坐标系

[19] Paul Martz 撰写的 OpenGL 变换管道

[20] 宋浩安的齐次坐标

[21] 用于科学可视化的 Python 和 OpenGL，版权所有 (c) 2018 - Nicolas P. Rougier

[22] ASPOSE 撰写的 SVG 坐标系和单位

[23] Sara Soueidan 撰写的 svg-coordinate-systems

[24] 二维坐标系，伦敦大学金史密斯学院

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]