消歧义

平面的指数映射是

是平面的指数变换

平面的指数映射不是

指数函数（指数映射）的茱莉亚集合或曼德博集合，例如指数曼德博集合 z := exp(z) + c
一个轴上的对数刻度^[1]
两个轴上的对数刻度：对数-对数刻度图^[2]
极方位等距投影（黎曼几何中的指数映射）^[3]
指数算子，可以应用于灰度图像的变形算子。^[4]

比较不同输入下的指数函数

单个数字（0D 空间）给出数字的自然指数
数轴（1D 空间）。指数刻度不用。对数刻度用于指数数据。它给出线性函数。^[5]
平面（2D 空间）给出指数映射

数字

在数学中，对数是指数运算的逆函数。这意味着以 b 为底的数字 x 的对数是指将 b 提高到该指数，以产生 x

y=\log _{b}x

等同于

x=b^{y}

如果 $b$ 是一个正实数。（如果 $b$ 不是一个正实数，则指数和对数都可以定义，但可能取多个值，这使得定义变得更加复杂。）^[6]

对数函数和指数函数
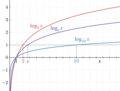
对数函数的图，具有三个常用的底数。特殊点 $log b b = 1$ 由虚线表示，所有曲线在 $log b 1 = 0$ 交汇
以 2 为底的对数图在x轴处交于 $x = 1$ ，并通过点 (2, 1)，(4, 2) 和 (8, 3)，例如， $log 2 (8) = 3$ 和 $23 = 8$ 。该图无限接近于y轴，但不会与之相交

实指数函数是从 $\mathbb {R}$ 到 $(0;\infty )$ 的双射。^[7] 它的逆函数是自然对数，记作 $\ln ,\log ,\log _{e};$ ；因此，一些旧的文本将指数函数称为反对数。

尺度

对数刻度（或对数刻度）是一种以紧凑的方式显示数值数据跨越非常大范围的值的方法——通常数据中最大的数字比最小的数字大数百甚至数千倍。这种刻度是非线性的：在对数刻度上，数字 10 和 20 以及 60 和 70 之间的距离并不相同。相反，数字 10 和 100 以及 60 和 600 的间距是相等的。因此，沿着刻度移动一个单位距离意味着该数字已乘以 10（或其他固定因子）。通常，指数增长曲线会显示在对数刻度上，否则它们会增长得太快，无法容纳在小型图表中。另一种思考方式是数据的位数以恒定的速度增长。例如，数字 10、100、1000 和 10000 在对数刻度上是等距的，因为它们的位数每次增加 1：2、3、4 和 5 位。这样，增加两位数会使对数刻度上测量的量乘以 100。

对数刻度

在 1 个轴上 = 半对数图^[8]
- 线性-对数图
- 对数-线性图
在两个轴上 = 对数-对数图^[9]

Lin-Lin 刻度
Log-Lin 刻度
Lin-Log 刻度
Log-Log 刻度

对数刻度用于指数数据。它给出线性函数。^[10]^[11]

映射

道格拉斯·N·阿诺德的复变函数图形:
- "复指数函数将以正负πi为界的无限开带一一映射到平面减去负实轴。
- 实部为常数的直线映射到圆，而虚部为常数的直线映射到从原点出发的射线。
- 在动画中，我们查看的是带内的一个矩形，而不是整个带，因此覆盖的区域是一个环减去负实轴。
- 环的内边界非常靠近原点，几乎不可见。
- 我们还使带的宽度略小于2π，以便环不会完全闭合."
- 复指数函数将矩形|Re(z)| ≤ a，|Im(z)| ≤ π映射到环 $e^{-a}\leq |w|\leq e^{a}$
保罗·福尔斯特德的复变函数组合查看器 - 选择的映射函数的组合：g(f(z))。需要增加网格大小才能获得相同的效果（矩形到环的映射）。
复指数函数作者：苏珊·阿丁顿
复变函数映射作者：胡安·卡洛斯·庞塞·坎普萨诺
复指数函数作者：滨田达吉 : 复指数函数将矩形域映射到扇形图像（穿孔圆的部分或完整扇区）
复指数映射由 Siamak 在 GeoGebra 上绘制:
- 垂直轴被变换到 w 平面的圆上
- 水平轴被变换到 w 平面的半径上
(保角)指数映射下 [-3,3]x[-3,3] 大小的正方形网格的图像几乎是完整的环^[12]
复指数函数将矩形 [-1,1]x[0 ,pi/2] 双全纯映射到四分之一环 $[e^{-1},e]x[e^{-1},e]$ ^[13]
太平洋科技的复指数函数 24 个视图
Mathematica 问题：如何将 expz 作为复变映射可视化

虚拟数学博物馆：保角映射，复指数函数"笛卡尔网格被“保角地”映射到极坐标网格（即保持角度）：实轴的平行线被映射到径向线，而平行于虚轴的长度为 2π 的线段被映射到以 0 为中心的圆."

exp(x + i · y) = exp(x) · exp(i · y) = exp(x) · cos(y) + i · exp(x) · sin(y)

表示复指数的曲面
实部
虚部
模量 = cabs
主幅角 = carg

表示复指数的密度曲线
实部
虚部

指数映射
对数极坐标映射。点 (x,y) 被映射到 $(\rho ,\theta )$ 其中 $\rho =\log {\sqrt {x^{2}+y^{2}}}$ 和 $\theta =\arctan({\frac {y}{x}})$ 。一般来说，以原点为圆心，半径为 r 的圆被映射到水平线和垂直线。
墨卡托投影与旋转
从切空间到球体的指数映射

3D	2D	描述
$f(z)=\exp(z)$	$f(z)=\exp(z)$
$f(z)=\log(z)$	$f(z)=\log(z)$

周期

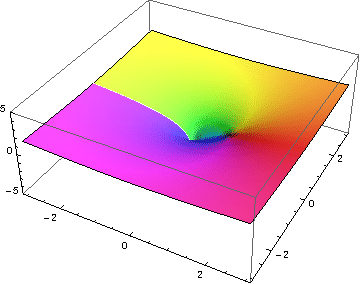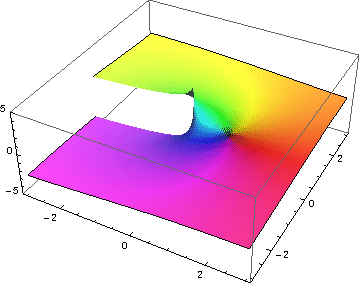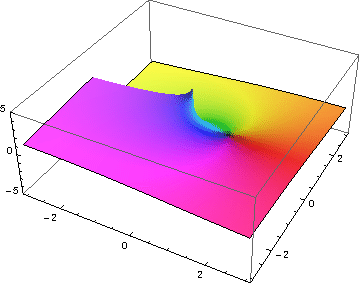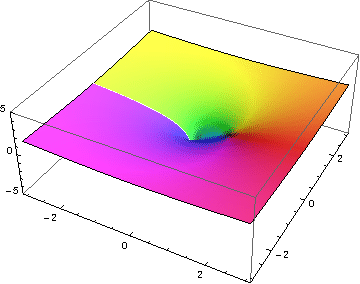指数函数是周期性的

exp(z + 2 π * i) = exp(z).

从公式中也可以清楚地看出周期性

exp(x + i * y) = exp(x) * (cos(y) + i * sin(y)) .

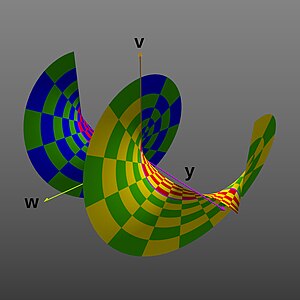
指数函数的图形是一个二维曲面 (x,y)，它在四维空间 (x,y,v,w) 中弯曲。

v+iw = exp(x+iy) 对于从 -1.5 到 1.5 的 x 值和从 -2π 到 2π 的 y 值，因此显示了螺旋的两个完整旋转。

名称

指数映射^[14]
指数映射^[15]^[16]^[17]
墨卡托（这不是一个好的名字，因为这里只是从平面复平面（二维笛卡尔平面）到指数平面的映射。这里没有从球面到平面复平面（笛卡尔平面）的映射^[18]）
- 墨卡托地图
- 墨卡托投影^[19]^[20]^[21]^[22]
极坐标投影
对数极坐标映射（对数极坐标）
对数^[23]
- 以点 c0 为中心的对数投影：z-> (log(|z-c0|)
log(z)-Mandelbrot-Zooms^[24] = 侧滚（侧滚分形缩放）^[25]^[26]^[27]

一般名称

图形投影
几何变换

描述

 Math notation

$map:\mathbb {C} \to \mathbb {C}$

$c_{e}\leftarrow e^{c}+c_{0}$

// c with complex type
complex double map(complex double c) {
return c_e = cexp(c) + c0; }

// c without complex type
cx_e = exp(creal(c)) * cos(cimag(c)) + realpart(c0); // real part of c_e
cy_e = exp(creal(c)) * sin(cimag(c)) + imagpart(c0); // imag part of c_e

特点

映射

笛卡尔平面上的矩形到极坐标的二次扇区，
x 映射到半径，y 映射到角度（弧度）^[28]

水平方向
- 映射 $c_{0}$ 到无穷大（序列的极限 = MF = Myrberg-Feigenbaum 点 = Feigenbaum 点)
- 将与上述序列相关的关键组件映射到相同大小
垂直方向
- 垂直坐标是以 $2\pi$ 为周期的，因为它们使用了三角函数

例子

周期为 $p=1*2^{n}$ （周期倍增级联）的根点序列，并且该序列的极限点是 Myrberg-Feigenbaum 点 $\mathbf {MF} _{1/2}=c_{0}=-1.401155...$
周期为 $p=1*3^{n}$ 的根点序列，并且该序列的极限点是 Myrberg-Feigenbaum 点 $\mathbf {MF} =c_{0}=-1.7864402555636388747...$

非正式描述

指数映射将整个复平面转换为一个条带，该条带沿实轴无限延伸，沿虚轴的宽度为 2π。指数映射来自曼德尔布罗集词汇表和百科全书，作者罗伯特·穆纳福，(c) 1987-2022
" 其思想是专注于曼德尔布罗集内或附近的某个点，并创建一个图像，其中一个方向是距离的对数，另一个方向是角度。结果非常类似于 astro-ph/031571 地图^[29] 和 XKCD 漫画版本。^[30] 该地图投影是共形的，因此它不会扭曲局部角度，并且物体通常在所有尺度上都是可识别的。" 安德斯·桑德伯格^[31]
曼德尔布罗集的图像，以 c0 为中心，采用对数投影：z-> (log(|z-c0|), arg(z-c0))。安德斯·桑德伯格 ^[32]
" 它是一个朝向目标点的对数映射（或者，正如有些人可能说的那样，一个以目标点为南极、复数 ∞ 为北极的墨卡托投影）；水平方向是周期性的，我将两个周期并排放置，而垂直方向则在顶部和底部延伸到无穷大，这对应于无限地放大或缩小，每次一个水平周期的尺寸为 exp(2π)≈535.5。对数映射上的水平线（“平行线”）对应于目标点的同心圆，垂直线对应于从目标点发出的半径；并且变形保持角度。" 戴维·马多尔 ^[33]
" 坐标系使得角度分量映射到结果图像的 y 轴，半径映射到 x 轴。此外，x 轴（半径）使用 exp 函数进行归一化，以便在该映射中保留角度。 " 米卡·塞帕 ^[34]
log : " 为了说明曼德尔布罗集边界的复杂性，图 8 显示了 dM 在变换 log(z - c) 下的图像，其中 c 为曼德尔布罗集边界的某个点。请注意，主心形的上右侧有一个尖点；在图中向左看对应于向点 c 放大。（具体来说，c = -0.39054087... - 0.58678790i...，该点位于主心形边界上，对应于黄金分割西格尔圆盘。）请注意，主心形的上右侧有一个尖点；在图中向左看对应于向点 c 放大。" ^[35]
" 传奇的横向滚动分形缩放。1 个月+（插值器+视频编辑器）= Log(z)。这意味着该位置的对数投影，这产生了这个有趣的横向滚动平面 ^^)" ^[36]
" 没有程序可以在 Log(Z) 平面渲染此分形。但你可以在 Ultra Fractal 或类似的具有可编程分布式的软件中制作它。公式为：C = exp(D)，其中 D 是你的可缩放坐标" SeryZone X
只是 c = c0 + cexp(x + i y) 和 x + i y = clog(c - c0)，以 2pi/width 缩放（克劳德）
想法
- J. Richard Gott III、Mario Jurić、David Schlegel、Fiona Hoyle、Michael Vogeley、Max Tegmark、Neta Bahcall、Jon Brinkmann 编著的《宇宙地图》
- XKCD 漫画版本

正式数学描述

正向变换

这里变换是 2 个变换的合成

复指数函数: $f(c)=e^{c}$
几何或复数平移 $t(x)=x+c_{0}$

  $c_{e}=t(f(c))$

c_{e}\leftarrow e^{c}+c_{0}

其中

c 是 c 平面（笛卡尔坐标系中的平面图像 = 两个轴上的线性刻度）中的一个参数点。它是二次映射 $z^{2}+c$ 的一个参数
$c_{e}$ 是新变换平面（对数极坐标图像）中的一个参数
$c_{0}$ 是一个常数参数（用于平移）。有时称为中心，但更好的名称似乎是：目标或极限点
e 是欧拉数，是一个数学常数，约等于 2.71828，

逆变换:

c=ln(c_{e}-c_{0})

其中

$ln$ 是自然对数

exp

复指数映射

复指数函数是周期性的，周期为 $2 πi$ ，并且 $\exp(z+2\pi ik)=\exp z$ 对所有 $z\in \mathbb {C} ,k\in \mathbb {Z}$ 成立。

指数函数将复平面中的任何直线映射到复平面中的对数螺旋线，中心位于原点。存在两种特殊情况

当原直线平行于实轴时，生成的螺旋线永远不会闭合自身；
当原直线平行于虚轴时，生成的螺旋线是某个半径的圆。

将复指数函数视为涉及四个实变量的函数： $v+iw=\exp(x+iy)$ 指数函数的图形是一个在四个维度上弯曲的二维曲面。

从 $xy$ 域的彩色编码部分开始，以下是该图形的不同投影到二维或三维空间中的表示。

复指数函数的图形
棋盘格键
$x>0:\;{\text{green}}$
投影到范围复平面 (V/W)。与下一个透视图像进行比较。
投影到 $x$ 、 $v$ 和 $w$ 维度，产生一个喇叭状或漏斗状的形状（想象成二维透视图像）。
投影到 $y$ 、 $v$ 和 $w$ 维度，产生螺旋形状。 ( $y$ 范围扩展到 $\pm 2\pi$ ，再次作为二维透视图像）。

第二张图展示了如何将域复平面映射到值域复平面。

零映射到 1
实数 $x$ 轴映射到正实数 $v$ 轴。
虚数 $y$ 轴以恒定角速度绕单位圆旋转。
具有负实部的值映射到单位圆内部。
具有正实部的值映射到单位圆外部。
具有恒定实部的值映射到以零为中心的圆。
具有恒定虚部的值映射到从零延伸的射线。

第三张图和第四张图展示了第二张图中的图形如何在其他两个维度（在第二张图中未显示）上延伸。

第三张图展示了沿实数 $x$ 轴延伸的图形。它展示了图形是关于实数指数函数图形的 $x$ 轴的旋转曲面，产生喇叭或漏斗形状。

第四张图展示了沿虚数 $y$ 轴延伸的图形。它展示了图形的曲面对于正负 $y$ 值并不真正沿负实数 $v$ 轴交汇，而是围绕 $y$ 轴形成螺旋曲面。由于它的 $y$ 值已扩展到 $\pm2 π$ ，此图也更好地描绘了虚数 $y$ 值中的 2π 周期性。

Log

复数对数作为共形映射^[37]

由于 ** $\log z$ ** 的一个分支是全纯的，并且由于它的导数 ** $\log z$ ** 从未为 0，它定义了一个共形映射。

例如，**主分支** $w=\operatorname {Log} z$ ，被视为从 $\mathbb {C} -\mathbb {R} _{\leq 0}$ 到由 $\left|\operatorname {Im} z\right|<\pi$ 定义的水平带的映射，具有以下属性，这些属性是极坐标形式公式的直接结果。

以 0 为中心的 _z_ 平面上的圆形映射到 _w_ 平面上的垂直线段，连接 $a-\pi i$ 到 $a+\pi i$ ，其中 _ $a$ _ 是圆形的半径的对数。
从 _z_ 平面上的 0 发出的射线映射到 _w_ 平面上的水平线。

如上，_z_ 平面上的每个圆形和射线在直角处相遇。它们的 Log 映射图像是 _w_ 平面上的垂直线段和水平线（分别），它们也以直角相遇。这是 Log 的共形特性的说明。

程序员说明

// https://code.mathr.co.uk/mandelbrot-graphics/blob/HEAD:/c/lib/m_d_transform.c
static void m_d_transform_exponential_forward(void *userdata, double _Complex *c, double _Complex *dc) {
  m_d_transform_exponential_t *t = userdata;
  double _Complex c0 = *c;
  double _Complex dc0 = *dc;
  *c = cexp(c0) + t->center;
  *dc = dc0 * cexp(c0);
}


static void m_d_transform_exponential_reverse(void *userdata, double _Complex *c, double _Complex *dc) {
  m_d_transform_exponential_t *t = userdata;
  double _Complex c0 = *c;
  double _Complex dc0 = *dc;
  *c = clog(c0 - t->center);
  *dc = dc0 / (c0 - t->center);
}

从 MathMap 过滤墨卡托

filter mercator (image in)
   in(xy*xy:[cos(pi/2/Y*y),1])
end

Maxima CAS 源代码

(%i1) kill(all);
(%i2) display2d:false;
(%i3) ratprint : false; /* remove "rat :replaced " */
(%i4) c:cx +cy*%i$
(%i5) c0:c0x+c0y*%i$
(%i6) realpart(c0 + exp(c));
(%o6) %e^cx*cos(cy)+c0x
(%i7) imagpart(c0 + exp(c));
(%o7) %e^cx*sin(cy)+c0y
(%i8) cabs(c0 + exp(c));
(%o8) sqrt((%e^cx*sin(cy)+c0y)^2+(%e^cx*cos(cy)+c0x)^2)
(%i9) carg(c0 + exp(c));
(%o9) atan2(%e^cx*sin(cy)+c0y,%e^cx*cos(cy)+c0x)

笔记

该映射是**周期性的**，因为内部有三角函数。

(%i1) kill(all);
(%i2) display2d:false;
(%i3) ratprint : false; /* remove "rat :replaced " */
(%i4) ce:ceex+cey*%i;
(%i5) c0:c0x+c0y*%i;
(%i6) realpart(log(ce - c0));
(%o6) log((cey-c0y)^2+(ceex-c0x)^2)/2
(%i7) imagpart(log(ce - c0));
(%o7) atan2(cey-c0y,ceex-c0x)

// https://www.foerstemann.name/dokuwiki/doku.php?id=log_z_-mandelbrot-zooms
// log(z)-Mandelbrot-Zooms by 
<languageVersion: 1.0;> 
kernel zoomer
< namespace : "Zoomer"; vendor : "private"; version : 2; description : "zoomer 2"; >
{
  const float PI = 3.14159265;
  const float EU = 2.71828; 
  parameter float translate <       
      minValue:float(0);
      maxValue:float(400.0); 
      defaultValue:float(0.0); >;
  parameter float rotate <       
      minValue:float(0.0);
      maxValue:float(960.0); 
      defaultValue:float(0.0); >;
  input image4 iImage1;
  input image4 iImage2;
  input image4 iImage3;
  input image4 iImage4;
  output float4 outputColor;
  void evaluatePixel()
  {
      float2 position = outCoord() - float2(479.5,199.5);
      float2 tmp = outCoord();
      tmp.y = abs(log(sqrt(pow(position.x,2.0) + pow(position.y,2.0))/510.0))*30.474;
      tmp.x = mod((atan(position.x, position.y)/PI + 1.0)*480.0, 958.5) ;
      position = tmp + float2(rotate,translate);
      position.x = mod(position.x,958.5)+1.0;
      if ( position.y < 398.5) {outputColor = sampleLinear( iImage1, position );} 
      else if ( position.y < 797.0) {outputColor = sampleLinear( iImage2, position - float2( 0.0 , 398.0 ));} 
      else if ( position.y < 1199.5) {outputColor = sampleLinear( iImage3, position - float2( 0.0 , 796.0 ));}
      else {outputColor = sampleLinear( iImage4, position - float2( 0.0 , 1194.0 ) );}  
  }
}

中心

$c_{0}$ 是一个常数参数（用于平移 = 偏移）。

它有时被称为中心，但更好的名称似乎是

目标
极限点
偏移或平移

目标点（中心）被投影到指数映射视图中的 -∞+0i。它将在最左边无限远，并且在图像上不可见。

缩放

图像的最左列具有最小缩放（最大的平面半径）
图像的最右列具有最大缩放（最小的平面半径）

指数网格扫描

约定

Robert Munafo 基于水平像素坐标生成角度，并基于垂直像素坐标生成半径（图像处于垂直位置，它位于较短的尺寸上）
通常的方法是从垂直像素坐标获得角度（图像处于水平位置，它位于较长的尺寸上）

具有指数坐标映射的网格扫描与平面图像的标准扫描不同。

for (int j = 0; j < h; ++j) { // vertical coordinate = number of the rows
    
     double e_angle = ((double) j) * px / r * 3.14159265359;  // Robert's way:  angle from 0 to 2π. 
   
   for (int i = 0; i < w; ++i) { // horizontal coordinate = number of the columns
    
       e_radius = ((double) i) * px / r * 3.14159265359;
       .....
    }

描述

图像宽度是最大像素数 = 图像以像素为单位的宽度（整数）

这里

像素坐标 j 从 0 到图像高度 - 1
因此 j/像素高度从 0.0 到 1.0
因此角度从 0 到 2 pi

Claude 的方法在数学上是正确的：角度通常被认为是从 -π 到 π，而不是从 0 到 2π。要解决这个问题，您可以在从其计算角度之前调整像素坐标。更改此

double e_angle = ((double) j) * px / r * 3.14159265359;

为此

double e_angle = ((double) (j-h/2)) * px / r * 3.14159265359;

笔记

e_radius 是 i 的线性函数
e_angle 是 j 的线性函数

计算像素坐标

以下是由 Robert Munafo 提供的示例^[39]

   /* Inputs are:
     ctr_r is the real coordinate of the center of the view we want to plot
     ctr_i is the imaginary coordinate of the center of the view
     
     real_width is the width of the image (in real coordinates). this should reflect the width when "zoomed in" all the way
     
     pixel_width is the number of pixels per row of the image we want to create
     pixel_height is the number of rows of pixels, or pixels per column
  
     This setup code computes:
     px_spacing is the width of the image (in real coordinate)
       divided by the number of pixels in a row
     halfwidth is half the width of the image (in real coordinate)
     halfheight is half the height of the image (in imaginary coordinate)
     min_r is the real coordinate of the left edge of the image
     max_i is the imaginary coordinate of the top of the image
  */
  void setup()
  {
    px_spacing = real_width / pixel_width;
    halfwidth = real_width / 2.0;    
    halfheight = halfwidth * pixel_height / pixel_width;
    min_r = ctr_r - halfwidth;
    max_i = ctr_i + halfheight;
  }
  

  /* Plot a single pixel, row i and column j. Use as many rows as you need
     for the image to show the whole Mandelbrot set. */
  void pixel_53(int i, int j, int itmax)
  {
    double cr, ci, offset_r, offset_i, angle, log_radius;
  
    /* compute angle and radius. Note that pixel_width is the number of
       pixels wide of the image, and j goes from 0 to pixel_width-1. This
       means that "j/pixel_width" goes from 0.0 to 1.0, and therefore
       angle goes from 0 to 2 pi. log_radius needs to be computed the
       same way in order for shapes to be preserved, which happens because
       the complex exponential function is a conformal map.
    Important: the row coordinate i can be as big as you want: add as many
       rows of pixels as are needed for the "log_radius" to get close to 1.
       This ensures that exp(log_radius) gets big enough to go beyond the
       area that has the Mandelbrot set in it. */
    angle =      (((double) j) / pixel_width) * 2.0 * 3.14159265359;
    log_radius = (((double) i) / pixel_width) * 2.0 * 3.14159265359;
  
    /* compute offsets = translation = add complex number offset */
    offset_r = cos(angle) * halfwidth * exp(log_radius);
    offset_i = sin(angle) * halfwidth * exp(log_radius);
  
    ci = ctr_i + offset_i;
    cr = ctr_r + offset_r;
    evaluate_and_plot(cr, ci, itmax, i, j);
  }

与

Claude Heiland-Allen 的指数条带进行比较：最终视频的渲染可以通过在重新投影到一系列平面图像之前，围绕缩放中心计算指数间隔的环来加速。如果出现问题，请访问：https://mathr.co.uk/mandelbrot/exponential_strip.svg

纵横比

为了获得最佳（更共形）结果，请使用宽纵横比（9:1 效果很好，窗口大小为 1152x128 或 1536x170）。

比例因子 R

为了最大程度地减少需要计算的像素总数，这与^[40]成正比

 $K={\frac {R^{2}-1}{logR}}$

用以下公式定义缩放效率：

 ${\frac {2}{K}}$

那么

传统的 R=2 的效率只有 46%，
R=4/3 的效率为 74%
R=8/7 的效率为 87%

其中

视频图像大小为 W×H

视频

图像

类别：曼德勃罗特集合 - commons 中的墨卡托投影

无变换
实数（= 1D）版本
1D：3 个具有非线性（即对数）x 轴比例的窗口
复数（= 2D）版本
正投影
极坐标投影
M(3,1) Misiurewicz 在 1E10 倍放大率下（底部）使用指数映射
GIMP 中的墨卡托效果，使用 MathMap

两张具有相同参数的图像。在上图中，主天线位于两侧，在下图中位于图像的中心

墨卡托
靠近 Myrberg-Feigenbaum 点区域的映射图。主曼德勃罗特集合的芽以几何方式收敛到该点（以 Feigenbaum 常数设定的速率），在顶部和底部产生规律间隔的芽。由于我没有它的精确坐标，因此该地图的中心略微偏离。
此图像对应于围绕一个点的 10^30 倍缩放（我只使用了 30 位精度，因此左侧边缘存在伪影
此图像对应于围绕一个点的 10^30 倍缩放（我只使用了 30 位精度，因此左侧边缘存在伪影）。
10^60 倍缩放。条带结构的出现是因为缩放穿过围绕较小曼德勃罗特集合的嵌入朱利亚集合；每个经过缩放的新曼德勃罗特集合都会将其自己的朱利亚集合添加到序列中。中心点为 c=-1.256827152259138864846434197797294538253477389787308085590211144291 +0.37933802890364143684096784819544060002129071484943239316486643285025i
$Zooms of the Mandelbrot set around a point projected so that the distance to the point forms a logarithmic scale. Details on the left edge are ~10^15 times smaller than on the right edge. The rightmost black blob in the pictures is the main "continent" of the set. Satelite sets of different sizes can be seen linked by fractal chains of varying complexity. The colors are set using the distance estimator method.$

曼德勃罗集在某一点周围的缩放，投影方式使该点距离形成对数刻度。左边缘的细节比右边缘小约 10^15 倍。图片中最右边的黑色斑点是集合的主要“大陆”。不同大小的卫星集可以通过不同复杂程度的分形链连接起来。颜色使用距离估计器方法设置。

如何从指数图像中读取位置？

fractalforums.org : 你能找到这个分形的位置吗？
"使用复数对数函数进行逆映射（将计算所需数据的在条带中的位置，以正常正交坐标空间中的给定位置表示）" Robert Munafo^[41]

提示

图像不具有对称性（上下），因此 c0 的虚部不为零

实现

分形程序

fraktaler-3
UltraFractal
fractalzoomer 中的 Polar_Projection
Fractalshades - Geoffroy Billotey 编写的 Python 程序
emndl: 曼德勃罗集的指数条带可视化，Claude Heiland-Allen 编写的程序
pfract - Mika Seppä 编写的控制台 C 程序
emndl: mathr 的指数条带曼德勃罗集渲染器: 它为: c = c0 + cexp(x + i y) 并且 x + i y = clog(c - c0)，宽度缩放 2pi/width
Fractalshades 文档 : P01-feigenbaum expmap

Kalles Fractaler 和 zoomasm

最终视频的渲染可以通过在重新投影到一系列平面图像之前，计算围绕缩放中心的指数间隔环来加速。
kf-2.15 支持以指数映射形式渲染 EXR 关键帧
zoomasm 可以将以上关键帧组装成缩放视频。zoomasm 从 EXR 开始，包括原始迭代数据，并且颜色算法可以编写在 OpenGL 着色器源代码片段中
Claude Heiland-Allen 编写的 kf-extras - 具有指数映射（也称为对数极坐标或墨卡托投影）转换器

OpenCV

ImageMagic

processing

forum.processing : how-to-change-an-image-from-x-y-coordinate-to-polar-coordinate

sci-kit

Mathworks

David Young 来自 mathworks 的对数极坐标图像采样版本 1.0.0.0 (4.33 KB)

glsl

一个典型的着色器看起来像这样（Thorsten Förstemann 编写的代码）

// https://web.archive.org/web/20210715234846/https://www.foerstemann.name/dokuwiki/doku.php?id=log_z_-mandelbrot-zooms
<languageVersion: 1.0;> 
kernel zoomer
< namespace : "Zoomer"; vendor : "private"; version : 2; description : "zoomer 2"; >
{
  const float PI = 3.14159265;
  const float EU = 2.71828; 
  parameter float translate <       
      minValue:float(0);
      maxValue:float(400.0); 
      defaultValue:float(0.0); >;
  parameter float rotate <       
      minValue:float(0.0);
      maxValue:float(960.0); 
      defaultValue:float(0.0); >;
  input image4 iImage1;
  input image4 iImage2;
  input image4 iImage3;
  input image4 iImage4;
  output float4 outputColor;
  void evaluatePixel()
  {
      float2 position = outCoord() - float2(479.5,199.5);
      float2 tmp = outCoord();
      tmp.y = abs(log(sqrt(pow(position.x,2.0) + pow(position.y,2.0))/510.0))*30.474;
      tmp.x = mod((atan(position.x, position.y)/PI + 1.0)*480.0, 958.5) ;
      position = tmp + float2(rotate,translate);
      position.x = mod(position.x,958.5)+1.0;
      if ( position.y < 398.5) {outputColor = sampleLinear( iImage1, position );} 
      else if ( position.y < 797.0) {outputColor = sampleLinear( iImage2, position - float2( 0.0 , 398.0 ));} 
      else if ( position.y < 1199.5) {outputColor = sampleLinear( iImage3, position - float2( 0.0 , 796.0 ));}
      else {outputColor = sampleLinear( iImage4, position - float2( 0.0 , 1194.0 ) );}  
  }
}

Python

stackoverflow 问题: image-information-along-a-polar-coordinate-system

这样创建的图像也称为

指数映射
墨卡托-曼德勃罗集映射
黎曼数球的墨卡托投影。^[42]^[43]

在以下程序示例中，计算了曼德勃罗集的对数投影，

曼德勃罗集使用 NumPy 通过复数矩阵进行计算。使用 David Madore 和 Anders Sandberg 提出的一种对数投影。这种投影使得缩放动画的计算更加容易

对数投影允许创建极速加速的曼德勃罗集缩放动画（另请参阅 Thorsten Förstemann 的动画和 Claude Heiland-Allen 的坐标分析 ^[44]^[45]^[46]^[47]

import numpy as np
import matplotlib.pyplot as plt

d, h = 200, 1000  # Pixeldichte (= Bildbreite) und Bildhöhe
n, r = 800, 5000  # Anzahl der Iterationen und Fluchtradius (r > 2)

x = np.linspace(0, 2, num=d+1)
y = np.linspace(0, 2 * h / d, num=h+1)

A, B = np.meshgrid(x * np.pi, y * np.pi)
C = 4.0 * np.exp((A + B * 1j) * 1j) + (- 1.748764520194788535 + 3e-13 * 1j)

Z, dZ = np.zeros_like(C), np.zeros_like(C)
D = np.zeros(C.shape)

for k in range(n):
    M = Z.real ** 2 + Z.imag ** 2 < r ** 2
    Z[M], dZ[M] = Z[M] ** 2 + C[M], 2 * Z[M] * dZ[M] + 1

N = abs(Z) > 2  # Distanzschätzung des Außenbereichs
D[N] = np.log(abs(Z[N])) * abs(Z[N]) / abs(dZ[N])

plt.imshow(D.T ** 0.05, cmap=plt.cm.nipy_spectral, origin="lower")
plt.savefig("Mercator_Mandelbrot_map.png", dpi=200)