交通运输基础/排队论

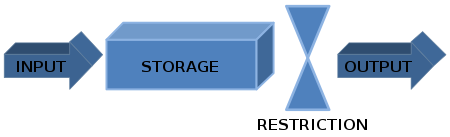
排队系统的示意图

排队论研究的是在需求超过可用容量的特定路段附近的交通行为。排队现象在许多常见情况下都能看到：乘坐公共汽车、火车或飞机，高速公路瓶颈，购物结账，下课时离开教室门口，等待实验室的电脑，麦当劳的汉堡包，或者理发店的理发。在交通工程中，排队可能发生在红绿灯、停车标志、瓶颈或任何基于设计或交通的流量收缩处。如果处理不当，排队会导致严重的网络拥堵或“交通堵塞”情况，因此工程师必须对其进行研究和理解。

累积输入输出图（Newell曲线）

显示排队累积输入和输出的Newell曲线

基于出发率和到达率对数据，可以得到每辆车的延迟。利用图中所示的输入输出 (I/O) 排队图，可以找到每辆车的延迟：第$i^{th}$辆车的延迟是出发时间减去到达时间（$t_{2}-t_{1}$）。总延迟是每辆车延迟的总和，也就是到达（A(t)）和离开（D(t)）曲线之间三角形的面积。

分布

到达分布 - 确定性（均匀）或随机（例如泊松）

服务分布 - 确定性或随机

服务方式

• 先到先服务（FCFS）或先进先出（FIFO）
• 后到先服务（LCFS）或后进先出（LIFO）
• 优先级（例如，匝道计量器上的HOV绕行）

排队特征

队列长度特征 - 有限或无限

通道数量 - 等待队列的数量（例如，匝道=2，超市=12）

我们使用以下符号

• 到达率 = $\lambda$
• 离开率 = $\mu$

利用率 $\rho ={\frac {\lambda }{\mu }}\,\!$

饱和度

过饱和：$\lambda >\mu$

欠饱和 $\lambda <\mu$

饱和 $\lambda =\mu$

Little公式

交通队列

Little 公式: $E(n)=\lambda E(v)$

这意味着平均队列长度（以车辆为单位）等于到达率（每单位时间车辆数）乘以平均等待时间（包括排队延迟时间和服务时间）（以时间单位计）。该结果与特定的到达分布无关，虽然可能很明显，但这是一个重要的基本原理，直到 1961 年才被证明。

更多应用请参阅维基百科文章。

无容量约束队列 (M/D/1) 和 (M/M/1)

随机排队队列长度.png

随机排队和确定性排队以及 BPR 的比较。

随机排队与 BPR 和 Akcelik 公式的比较。

已经表明，M/D/1 和 M/M/1 排队的队列长度、等待时间和延迟不同。这些差异体现在公式中，并在下面显示。请注意两者之间的细微差异。

M/D/1 和 M/M/1 队列属性的比较

	M/D/1	M/M/1
E(w)（平均等待时间）	$E(w)={\frac {\rho }{2\mu \left({1-\rho }\right)}}\,\!$	$E(w)={\frac {\lambda }{\mu \left({\mu -\lambda }\right)}}\,\!$
E(v)（平均总延迟）	$E(v)={\frac {2-\rho }{2\mu \left({1-\rho }\right)}}\,\!$	$E(v)={\frac {1}{\left({\mu -\lambda }\right)}}\,\!$
E(n)（系统中单位（包括正在服务的车辆）的预期数量）	$E(n)={\frac {(2-\rho )\rho }{2(1-\rho )}}\,\!$	$E(n)={\frac {\rho }{1-\rho }}\,\!$

注释

• 平均等待时间 (E(w)) 不包括服务时间。
• 平均总延迟 (E(v)) 为（等待时间 + 服务时间）。由于瓶颈的存在，有时也将其称为平均延迟时间。
• 系统中单位的预期数量 (E(n)) 包括当前正在服务的客户（以单位数计）。根据 Little 公式，这是到达率乘以在系统中花费的平均时间$E(n)=\lambda *E(v)$。
• 有时需要请求队列中单位的预期数量 (E(m))，不包括正在服务的客户，这需要使用不同的公式（到达率乘以平均等待时间$E(m)=\lambda *E(w)$），并且显然会得到一个较小的数字。

无容量约束队列 (M/M/1)（随机到达和随机服务）

除了之前提到的属性外，M/M/1 排队还有一些其他需要注意的属性。

其他 M/M/1 队列属性

	M/M/1
系统中 n 个单位的概率	$P\left(n\right)=\rho ^{n}\left({1-\rho }\right)\,\!$
到达的平均等待时间，包括排队和服务	$E\left(v\right)={\frac {1}{\left({\mu -\lambda }\right)}}\,\!$
队列中的平均等待时间（不包括正在服务的车辆）	$E\left(w\right)={\frac {\lambda }{\mu \left({\mu -\lambda }\right)}}\,\!$
系统中单位数量的期望值（包括正在服务的车辆）	$E\left(n\right)=\lambda E(v)={\frac {\lambda }{\mu -\lambda }}\,\!$
平均排队长度（不包括正在服务的车辆）	$E\left(m\right)=\lambda E(w)={\frac {\lambda ^{2}}{\mu \left({\mu -\lambda }\right)}}\,\!$
在系统中花费时间小于或等于t的概率	$P\left({v\leq t}\right)=1-e^{-\left({1-\rho }\right)\mu t}\,\!$
在排队中花费时间小于或等于t的概率	$P\left({w\leq t}\right)=1-\rho e^{-\left({1-\rho }\right)\mu t}\,\!$
在排队中花费时间超过t的概率，前提是排队不为空	$P\left({w>t}\right|{w>0})=e^{-\left({1-\rho }\right)\mu t}\,\!$
排队车辆数量超过N的概率	$P\left({n>N}\right)=\rho ^{N+1}\,\!$

等待时间如何随容量利用率变化

容量受限的排队（有限）

容量受限的排队允许最多一定数量的车辆等待，因此与无容量限制的排队具有不同的特性。对于单通道欠饱和有限排队，其中系统中最大单位数量指定为$N$，并且具有随机到达和离开($\lambda ,\mu$)，我们有

其他 M/M/1 队列属性

	M/M/1
系统中n个单位的概率	$P(n)={\frac {\left({1-\rho }\right)}{1-\rho ^{N+1}}}\left(\rho \right)^{n}\,\!$
系统中单位数量的期望值	$E(n)={\frac {\left(\rho \right)}{\left({1-\rho }\right)^{}}}{\frac {1-\left({N+1}\right)\left(\rho \right)^{N}+N\rho ^{N+1}}{1-\rho ^{N+1}}}\,\!$

队列产生的现实原因

道路:

• 几何瓶颈（车道减少、急弯、坡道）
• 事故和事件
• 交通信号灯和交叉路口控制
• 与其他交通方式平交（铁路道口、活动桥等）
• 收费站
• 匝道计量器
• “围观”效应
• 恶劣天气

火车和公交:

• 站台容量
• 检票口
• 售票窗口/售票机
• 火车最小安全间隔
• 安检点
• 火车进出站效率（轨道数量、道岔等）

航空和机场:

• 跑道
• 飞机指定最小安全跟随距离（政府规定）
• 飞机物理最小安全跟随距离（湍流产生等）
• 进近和离场的可用空域
• 售票柜台/值机手续
• 安检点
• 行李系统
• 航站楼飞机容量
• 航站楼内部乘客容量
• 恶劣天气

水运和海运:

• 船闸和水坝
• 港口容量
• 最小“安全”距离（由政府和物理学决定）
• 恶劣天气

太空飞行:

• 发射能力
• 轨道飞行器之间的最小间距
• 地球上的恶劣天气
• 不利的天体条件

示例

示例1

问题

问题

在克拉斯提汉堡店，如果顾客到达率是每分钟1人，服务率是每45秒1人，求平均排队人数、平均等待时间和平均总延迟时间。假设为M/M/1过程。

示例

解决方案

首先，我们将所有数据转换为分钟。

服务时间

${45/60}=0.75minutes\,\!$ 每位顾客。或者，您可以说服务员可以处理60/45 = 1/0.75 = 1.33位顾客/分钟。

到达率为每分钟1位顾客。

利用率$\rho =(60/60)/(60/45)=0.75$，这意味着服务员平均75%的时间都在忙碌。

平均排队人数 (E(n))

$E(n)={\frac {\rho }{1-\rho }}={\frac {0.75}{(1-0.75)}}=3\,\!$

$E(n)=\lambda E(v)=1*3.00$ 利特尔公式

平均等待时间

$E(w)={\frac {\lambda }{\mu \left({\mu -\lambda }\right)}}={\frac {1}{1.33\left({1.33-1}\right)}}=2.25\,\!$

平均延迟时间

$E(v)={\frac {1}{\left({\mu -\lambda }\right)}}={\frac {1}{\left({1.33-1}\right)}}=3=E(w)+servicetime=2.25+0.75\,\!$

比较

我们可以使用M/D/1方程计算相同的结果，结果如下表所示。

M/D/1 和 M/M/1 队列属性的比较

	M/D/1	M/M/1
E(n)（平均排队人数）	1.875	3
E(w)（平均等待时间）	1.125	2.25
E(v)（平均总延迟）	1.875	3

可以看出，与更随机的情况（M/M/1，既有随机到达又有随机服务）相关的延迟大于较不随机的情况（M/D/1），这是预料之中的。

示例2

问题

问题

荷马在不到1分钟、2分钟或3分钟内拿到他的汉堡包的可能性有多大？

示例

解决方案

$P\left({t\leq 1}\right)=1-e^{-\left({1-\rho }\right)\mu T}=1-e^{-\left({1-0.75}\right)1.333*1}=1-e^{-0.333}=0.283\,\!$

$P\left({t\leq 2}\right)=1-e^{-\left({1-\rho }\right)\mu T}=1-e^{-\left({1-0.75}\right)1.333*2}=1-e^{-0.667}=0.487\,\!$

$P\left({t\leq 3}\right)=1-e^{-\left({1-\rho }\right)\mu T}=1-e^{-\left({1-0.75}\right)1.333*3}=1-e^{-1}=0.631\,\!$

示例 3

问题

问题

在遇到为他做汉堡的“满脸青春痘的少年”之前，荷马等待超过 3 分钟的可能性是多少？

示例

解决方案

$P\left({w\leq 3}\right)=1-\rho e^{-\left({1-\rho }\right)\mu T}=1-0.75e^{-\left({1-0.75}\right)1.333*3}\,\!$

$P\left({w>3}\right)=1-P\left({w\leq 3}\right)\,\!$

示例 4

问题

问题

荷马前面有超过 5 个顾客的可能性有多大？

示例

解决方案

$P\left({n>5}\right)=\rho ^{N+1}=0.75^{6}=0.178\,\!$

思考题

问题

如何最小化排队等待时间？

解决方案

插队总是能起到作用，但这个问题将在不违反任何规则的情况下得到解答。想象一下，你出去吃饭，却发现你最喜欢的餐厅门口排着长队。你会怎么办？也许当时什么也做不了，但下次再去这家餐厅的时候，你可能会选择一个不同的时间。也许是更早的时间，以避免午餐或晚餐的高峰时段。在交通中也可以看到类似的决策。那些厌倦了在上班途中排队的人可能会尝试比高峰时段更早或（如果可能）更晚出发，以减少自己的出行时间。这通常效果不错，直到其他所有司机都想到了同样的办法，并将拥堵转移到不同的时间。

美国加州的两名摩托车骑手正在实施车道穿梭

为了最小化道路上排队的等待时间，一些地方允许在特定情况下进行车道过滤甚至车道穿梭。其他一些地方也曾考虑过这些措施，但没有成功。

“有证据（Hurt，1981）表明，在多车道道路（如州际公路）上穿梭于停着或缓慢行驶的汽车之间（即车道穿梭），与留在车道内并与其他车辆一起行驶相比，可以略微降低事故发生频率。”

示例问题

示例问题 1：收费站排队

问题 (解答)

示例问题 2：匝道计量排队

问题 (解答)

示例问题 3：匝道计量排队

问题 (解答)

变量

• A(t) = λ - 到达率
• D(t) = μ - 离开率
• 1/μ - 服务时间
• ρ = λ/ μ - 利用率
• Q - 平均排队长度，包括当前正在服务的顾客（以单位数量表示）
• w - 平均等待时间
• t - 平均延迟时间（排队时间 + 服务时间）

关键词

• 排队论
• 累积输入输出图（Newell 图）
• 平均排队长度
• 平均等待时间
• 系统平均总延迟时间
• 到达率，离开率
• 不饱和，饱和
• D/D/1，M/D/1，M/M/1
• 通道
• 泊松分布
• 服务率
• 有限（有容量）队列，无限（无容量）队列

外部练习

本次作业旨在为学生提供机会，让他们更好地理解两种排队理论：M/D/1 和 M/M/1。为了帮助计算本练习中所需的数值，提供了两个预格式化的电子表格。虽然这些电子表格提供了计算结果，但为了参考，下面列出了公式

$WT_{q}=({\frac {C_{\lambda }^{2}+C_{\mu }^{2}}{2C_{\lambda }^{2}}})({\frac {\rho }{1-\rho }}){\frac {1}{\mu }}\,\!$

其中

• $WT_{q}\,\!$：队列中客户的平均延迟
• $C_{\lambda }\,\!$：到达分布的变异系数（CV）
• $C_{\mu }\,\!$：离开分布的变异系数
• $CV\,\!$：标准差/均值；对于泊松过程，CV = (1/SqRt (均值))，对于恒定分布，CV = 0
• $\mu \,\!$：平均离开率
• $\lambda \,\!$：平均到达率
• $\rho \,\!$：利用率 = 到达率/服务率 $(\rho =\lambda /\mu )\,\!$

M/D/1 排队

从明尼苏达大学的 STREET 网站下载 M/D/1 排队的文件：M/D/1 队列电子表格

使用此电子表格，针对 10 种场景中的每一种运行 5 次模拟，使用下表中列出的到达和离开信息。换句话说，将相同的数据输入电子表格 5 次以捕获变化的种子，从而由于模型的敏感性而产生略微不同的答案。总共将运行 50 次模拟。

场景	1	2	3	4	5	6	7	8	9	10
到达率	0.01	0.025	0.05	0.1	0.2	0.3	0.4	0.5	0.6	0.7
服务率	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5

此外，找到所有十个场景的利用率。根据利用率和分布变异性，使用上述方程计算所有利用率值小于 1 的场景的平均延迟。

最后，在同一延迟-利用率图中总结从模拟和 WTq 方程获得的平均延迟。解释您的结果。随着利用率的增加，平均用户延迟如何变化？上述方程是否提供了平均延迟的令人满意的近似值？

M/M/1 排队

从明尼苏达大学的 STREET 网站下载 M/M/1 排队的文件：M/M/1 队列电子表格

使用此电子表格，针对 10 种场景中的每一种运行 5 次模拟，使用下表中列出的到达和离开信息。换句话说，将相同的数据输入电子表格 5 次以捕获变化的种子，从而由于模型的敏感性而产生略微不同的答案。总共将运行 50 次模拟。

场景	1	2	3	4	5	6	7	8	9	10
到达率	0.01	0.025	0.05	0.1	0.2	0.3	0.4	0.5	0.6	0.7
服务率	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5

同样，您需要为每个场景使用五个不同的随机种子。在延迟-利用率图中总结结果。解释您的结果（您不需要使用上面给出的 WTq 方程来计算 M/M/1 队列的延迟）。

其他问题

• 最后比较 M/M/1 队列和 M/D/1 队列。你能得出什么结论？（对于相同的平均到达率，用户在这两个排队系统中是否会遇到相同的延迟？为什么或为什么不？）
• 提供一个简短的示例，说明 M/M/1 可能是在何种情况下使用合适的模型。
• 提供一个简短的示例，说明 M/D/1 可能是在何种情况下使用合适的模型。

其他问题

• 其他问题
• 作业

视频

• 排队论导论
• 确定性队列
• 岩石漏斗实验
• 随机队列
• 随机队列 - 概率分布
• 排队 - 收费站示例