如何制作松木赛车/物理学

目录

• 首页
• 前言
• 规则
• 木块
• 轮子
• 轴
• 组装
• 物理学
• 附录

编辑

本模块包含一些关于松木赛车的简单物理学和一些化学知识。松木赛车将重力势能转换为平动动能（以及由此产生的速度）、旋转动能（旋转的轮子）和来自摩擦的热量。最快的赛车是起始时重力势能最大（重物在后部）、最终旋转动能最小（轻质轮子，一个抬起）且摩擦损失能量最少的赛车（适当的润滑和对准）。松木赛车是一个 5 盎司的实用物理学、化学和工程实验室。

松木赛车问题在下面以两种不同的方式进行处理：1）使用运动学方程；2）使用能量。这两种方法都同样有效，最终得到相同的结果。

运动学方程处理

我们将建立一个物理模型，考虑作用在松木赛车上的所有主要力。首先是重力，这是唯一（允许）的使赛车沿着斜坡加速的力。接下来，我们将考虑轴承对轮子的摩擦力和轮子踏板对轨道的摩擦力。最后，我们将考虑空气阻力及其对赛车运动的影响。

在本节中，我们将考虑一个理想化的汽车和赛道。汽车的质量为*M*，为 5 盎司 (141.7 克)，长度为*l*，为 7 英寸，车轮的质量为*m*，为 2.6 克，半径为*r*，为 0.5 英寸。赛道总长为*L*，由长度为 $L_{r}$ 的斜坡组成，斜坡的倾斜角度为 $\theta$，然后是一个长度为 $L_{f}$ 的水平路段，一直到终点。考虑到这种几何形状，起始高度的表达式为 $H=L_{r}\sin \theta$。为了简化问题，我们暂时不会考虑斜坡与水平路段之间的过渡。典型的松木赛道赛车的参数值为 $L_{r}=$ 8 英尺 (2.44 米)，$L_{f}=$ 24 英尺 (7.32 米)，$H=$ 4 英尺 (1.22 米)，以及 $\theta$ = 30$^{\circ }$.

同时，考虑一个不受外力作用的物体的运动方程。这将是汽车在赛道水平路段的运动情况，此时忽略了摩擦力和车轮旋转。在这种情况下，运动方程为

$a(t)=0\,;\,v(t)=v_{0}\,;\,d(t)=v_{0}t+d_{0}\,$,

其中，*a(t)* 为加速度，*v(t)* 为速度，*d(t)* 为时间为 *t* 时的距离。时间 *t=0* 时的初始距离和速度分别由 $d_{0}$ 和 $v_{0}$ 给出。

重力作用在坠落物体上的力

锤子和羽毛下降 - 阿波罗 15 号指令长大卫·斯科特证明伽利略是正确的。（1.38 MB，ogg/Theora 格式）。

首先考虑最基本情况，即质量为 *M* 的坠落物体（一个苹果？）。重力作用于该物体上的力由以下表达式给出：

$F_{g}=Mg\,$,

其中 *g* 是 重力加速度 (9.807 米/秒² = 32.17 英尺/秒²，在地球表面)。该力向下作用，导致物体加速向地球坠落。

该物体的运动方程（忽略摩擦力）如下：

$a(t)=g\,;\,v(t)=gt+v_{0}\,;\,d(t)={\frac {1}{2}}gt^{2}+v_{0}t+d_{0}\,$.

一个物体从 4 英尺（1.22 米）的高度落下需要 0.499 秒才能到达地面，并且最终速度达到 4.892 米/秒。如果该物体随后立即被转向在没有摩擦力的 24 英尺的平坦轨道上滑动，那么它将需要额外的 1.496 秒才能滑完整个轨道，总共需要 1.995 秒。

重力对松木赛车的影响

松木赛车不会直接向下坠落，而是沿着倾斜角为 $\theta$ 的斜坡向下行驶。只有沿轨道表面方向的重力分量才会导致赛车的加速度。由此产生的加速力为

$F_{a}=Mg\,\sin \theta \,$.

赛车只在倾斜角为 $\theta$ 的斜坡上加速。在平坦轨道部分，其中 $\theta =0$，此加速力变为零。这可以看作是具有减小的重力 $g_{\theta }$ 的加速度。

$g_{\theta }=g\,\sin \theta \,$.

这种减小的重力可以用于上述运动方程来求解赛车。在松木赛车初始坡度上，$v_{0}=0$ 且 $d_{0}=0$，因此（忽略摩擦力和车轮旋转）这些方程变为

$a(t)=g_{\theta }=g\,\sin \theta \,;\,v(t)=g_{\theta }t\,;\,d(t)={\cfrac {1}{2}}g_{\theta }t^{2}\,$.

沿着斜坡滚下的时间 $T_{r}$ 由下式给出

$d(T_{r})=L_{r}={\cfrac {1}{2}}g_{\theta }T_{r}^{2}\,$,

求解 $T_{r}$

$T_{r}={\sqrt {\cfrac {2L_{r}}{g_{\theta }}}}={\sqrt {\cfrac {2L_{r}}{g\sin \theta }}}\,}$.

斜坡底部最大速度为

$v(T_{r})=v_{max}=g_{\theta }T_{r}={\sqrt {2gL_{r}\sin \theta }}={\sqrt {2gH}}\,$.

对于理想斜坡，$T_{r}$ = 0.998 秒，$v_{max}$ = 4.892 米/秒。这个时间是上面自由落体情况的两倍，但获得的最大速度相同！

汽车在赛道平坦部分($\theta =0$)的运动方程，当$t>T_{r}$时，由以下给出

$a(t)=0\,;\,v(t)=v(T_{r})=v_{max}\,;\,d(t)=L_{r}+v_{max}(t-T_{r})\,;\,t>T_{r}\,$.

完成赛道平坦部分所需时间$T_{f}$ 为

$d(T_{r}+T_{f})=L_{r}+L_{f}=L_{r}+v_{max}T_{f}\,$.

求解$T_{f}$

$T_{f}={\cfrac {L_{f}}{v_{max}}}\,$.

完成这场比赛的理想汽车总时间为

$T=T_{r}+T_{f}={\cfrac {v_{max}}{g_{\theta }}}+{\cfrac {L_{f}}{v_{max}}}\,$.

平轨时间为 1.4953 秒，总时间为 2.4933 秒。由于达到了与自由落体情况相同的最大速度，因此（无摩擦）平轨时间相同。总时间包括沿着斜坡向下移动的额外半秒。

能量守恒

通过能量考虑可以获得对松木赛车物理的一些关键理解。通过这种思考，我们可以考虑系统中可用的势能以及车轮中的线性动能和旋转动能。上面我们只考虑了汽车沿斜坡向下移动和横穿赛道时的线性运动。事实上，车轮的旋转需要能量，从而从系统中消耗了本应用来加速汽车的能量。为了解释车轮的旋转，我们将考虑系统的能量。

我们将从系统中的势能开始，然后转向简单的线性情况，最后加上车轮的旋转。

势能

使松木赛车沿斜坡滚下的能量是势能（符号 $U_{g}$）。在斜坡底部，这种能量转化为动能（符号 $E_{k}\,$）。

势能可以用以下公式计算

$U_{g}=mgh\,$.

其中 m 是汽车的质量，$g$ 是重力加速度（在地球表面为 9.807 m/s² = 32.17 ft/s²），h 是汽车在起点斜坡上的高度（约 4 英尺 = 1.22 米）。一个 5 盎司的松木赛车中储存的势能约为 1.7 kg m²/s²= 1.7 J。1.7 焦耳的能量相当于 1.7 瓦的功率作用于一秒钟。

平动动能

动能可以用以下公式计算

$E_{k}={\frac {1}{2}}mv^{2}$.

其中 v 是汽车的速度（速度），以米每秒（国际单位制）测量。如果所有的势能都转化为动能，那么

$U_{g}=E_{k}\,$

并且，从上面代入，

$mgh={\frac {1}{2}}mv^{2}\,$

由于质量在等式两边，您可以将两边都除以 $m$ 并取消（移除）等式中的质量。

$gh={\frac {1}{2}}v^{2}\,$

并且，重新排列，速度可以从以下公式中找到

$v={\sqrt {2gh}}\,$

速度不取决于质量，正如伽利略在比萨斜塔上所证明的那样，在阿波罗 15 号着陆期间，大卫·斯科特在月球上进行了证明。任何从 1.219 米高处坠落物体的速度都是 4.890 m/s（11 英里/小时）。

旋转动能

向前移动并不是唯一的动能；旋转车轮也需要能量。每个车轮的旋转动能由以下公式给出

$E_{r}={\frac {1}{2}}I\omega ^{2}$,

其中 I 是车轮的惯性矩，ω 是角速度。由于我们只考虑车轮在赛道上不打滑的情况，因此角速度与线速度的关系为

$\omega =v/r\,$,

其中r是轮子的半径。一个半径为 r 且质量为 $m'$ 的圆环的惯性矩为

$I_{ring}=m'r^{2}\,$

对于圆盘，它为

$I_{disk}={\frac {1}{2}}m'r^{2}\,$

对于一个松木赛车轮，惯性矩可以近似为

$I=0.58\,mr^{2}\,$,

其中m是一个轮子的质量，r是轮子的半径。

因此，N个轮子的转动动能为

$E_{r}={\frac {N}{2}}(0.58\,mr^{2})\omega ^{2}={\frac {N}{2}}(0.58\,m)v\,^{2}\,$.

事实证明，在汽车最高速度 4.75 米/秒时，四个轮子中储存的能量为 0.094 焦耳（见下表）。与上面的 1.7 焦耳重力势能相比，几乎 6% 的能量存储在旋转的轮子中，大约 94% 的能量可用于汽车的向前速度。

如果我们再次将所有势能转化为动能，我们可以找到最大动能和速度

$U_{g}=E_{k}+E_{r}\,\Longrightarrow \,MgH={\frac {1}{2}}\left(Mv_{max}^{2}+0.58N\,mv_{max}\,^{2}\right)\,$.

求解速度，

$v_{max}={\sqrt {\cfrac {2gH}{1+0.58N{\cfrac {m}{M}}}}}\,={\sqrt {\cfrac {2gH}{\alpha _{R}}}}\,$

注意，这个结果再次独立于赛道的几何形状。旋转因子，它具有降低重力的效果，表示如下

$\alpha _{R}=1+0.58N{\cfrac {m}{M}}\,$.

此因子可与上述运动方程中的重力一起使用。它必须与由于赛道坡度引起的降低的重力相结合。所得的有效重力为

$g'_{\theta }={\cfrac {g\sin \theta }{\alpha _{R}}}\,$.

这个带有轮子旋转的降低的重力可以代入运动方程，以计算汽车在任何点的距离、速度和加速度。运动方程变为

$a(t)=g'_{\theta }={\cfrac {g\sin \theta }{\alpha _{R}}}\,;\,v(t)=g'_{\theta }t\,;\,d(t)={\cfrac {1}{2}}g'_{\theta }t^{2}\,$.

现在很清楚为什么最重的汽车是最快的：对于大的 M，$\alpha _{R}$ 接近 1，速度与无摩擦块的上述情况相同：4.9 米/秒。使用标准 3.6 克车轮，一辆 141.7 克（5 盎司）的汽车在轨道底部具有 4.75 米/秒的速度。一辆 113.4 克（4 盎司）的汽车具有 4.72 米/秒的速度。

轻车轮的优势也很明显。速度最慢的汽车是车轮质量最大的汽车。如果$m=M$（四个 35 克车轮在轨道上滚动！）速度为 2.7 米/秒。使用 3.6 克车轮，速度为 4.75 米/秒；使用 1 克轻车轮，速度为 4.85 米/秒。另一种看法是，轻车轮汽车的动能在车轮中的比例小于 2%，而标准车轮汽车的动能在车轮中的比例接近 6%。

只要车轮不接触地面，抬起一个车轮就会降低旋转能量。三轮（3.6 克）汽车的速度为 4.78 米/秒，而抬高轻车轮的汽车可以达到 4.86 米/秒。

理想化轨道

现在我们知道了理想化汽车能跑多快，让我们让它在理想化轨道上跑起来。典型的松木赛车轨道长 32 英尺，其中 4 英尺用于起跑门和制动装置，剩下 8.534 米用于行驶。轨道的第一个部分的坡度约为 20 度，有一个弯曲的过渡段，接着是一个平坦的段到终点。轨道可以用一个长度为$d_{1}$ 的直斜坡部分来近似，接着是一个长度为$d_{2}$ 的平坦部分。与使用弯曲轨道和数值积分 获得的结果相比，使用直线轨道近似计算的时间差异小于 0.001 秒。 对于直线轨道和 20 度坡度，$d_{1}$ = 3.564 米，$d_{2}$ = 4.970 米。汽车从零速度开始沿着斜坡段$d_{1}$ 行驶，并加速到速度$v\,$，平均速度为$v/2\,$。然后它以速度$v\,$ 行驶距离$d_{2}$。总时间为

$t=2{\frac {d_{1}}{v}}+{\frac {d_{2}}{v}}$

或 12.098/v 秒，如果速度以米/秒为单位给出。下表给出了不同条件下的行驶时间。

汽车速度和时间

条件	$h\,(m)$	$m\,(g)$	$m'\,(g)$	$v\,(m/s)$	$t\,(s)$
无摩擦块	1.219	任何	0	4.89	2.47
库存车轮	1.219	141.7	3.6	4.75	2.55
轻型（4 盎司）汽车	1.219	113.4	3.6	4.72	2.56
轻型车轮	1.219	141.7	1.0	4.85	2.49
一个抬高的车轮	1.219	141.7	2.7	4.78	2.53
轻型车轮，一个抬高	1.219	141.7	0.75	4.86	2.49
后轮偏置（原装车轮）	1.243	141.7	3.6	4.80	2.52

质心

到目前为止，我们已经将汽车近似为一个点质量，它从距离终点 1.219 米的高度开始，最终达到 0 米的高度。正如任何熟悉松木赛车的人都知道的那样，通常最好将质心尽可能地向后移动，部分原因是为了增加重力势能。将质心移到后面，汽车会快多少？考虑两辆汽车，汽车 A 的质心位于木块的中心，汽车 B 的质心位于扩展轴距配置的后面轴前 25.4 毫米（1 英寸），该轴距距离木块后部 15.9 毫米（5/8 英寸）。汽车 B 的质心比汽车 A 后移 47.6 毫米，在 30° 斜坡上高出 23.8 毫米。汽车 A 从 1.219 米的高度开始，（如上所示）最大速度为 4.75 米/秒，时间为 2.55 秒；汽车 B 从 1.243 米的高度开始，最大速度为 4.80 米/秒，时间为 2.52 秒。

摩擦力

图示说明作用在静止在斜面上的木块上的力。

摩擦 是两个相互接触的物体之间阻碍其相对运动的力。一般来说，摩擦力有两种类型——静摩擦和动摩擦。静摩擦力是抵抗运动的力。动摩擦力也称为滑动摩擦力，是在两个相对运动的物体之间产生的力。与松木赛车相关的主要摩擦类型是车轴在车轮上的动摩擦和车轮在赛道上滚动时的静摩擦。这两个方面将在下面进一步详细讨论。空气阻力被认为是一个特殊主题，将在下面详细讨论。

其他类型的摩擦，包括车轮内轮毂与车身、车轮外轮毂与车轴头、车轮与赛道导轨之间的接触，可以通过适当的汽车设计和调校来最大限度地减少或完全消除。

滑动（轴）摩擦

只要两个表面相互接触并处于相对运动状态，就会发生滑动摩擦。对于松木赛车，接触摩擦的主要来源是车轴在车轮上。这种摩擦发生在汽车“系统”内部，并且始终发生在金属车轴与塑料车轮之间。作用在车轴和车轮上的摩擦力 ($F'_{f}$) 如下

$F'_{f}=\mu N_{f}\,$,

其中 $N_{f}$ 是表面之间产生的正压力（垂直于接触面），$\mu$ 是摩擦系数。摩擦系数是两个相互接触的材料的属性。对于松木赛车，$\mu$ 的值为光滑塑料对金属约为 0.24，如果车轴经过抛光并使用石墨等润滑剂，可以降低到 0.10 或更低。

正压力是车身质量对车轴的力。在斜坡为 $\theta$ 的赛道上，所有承载车轴的总正压力为

$N_{f}=(M-Nm)g\cos \theta \,$,

其中 M 是汽车的质量，m 是车轮的质量，N 是承载车轮的数量。$M-Nm$ 对于一辆最大重量的汽车来说是 127.3 克，它有四个 3.6 克的承载车轮。

相对于赛道的摩擦力会因机械优势而降低，机械优势是车轮半径与车轮轴孔半径的比率。车轮每旋转一次，汽车行驶一个车轮周长：95.0 毫米。车轴每次旋转只在车轮轴孔周长上行驶 7.19 毫米。然后，车轮对车轴的摩擦力为

$F_{f}=\mu \left({\cfrac {r}{r_{B}}}\right)(M-Nm)g\cos \theta =\mu '(M-Nm)g\,$,

其中 $r_{B}$ 是车轮轴孔的半径，调整后的摩擦系数 $\mu '$ 为

$\mu '=\mu \left({\frac {r}{r_{B}}}\right)\,$.

由该力引起的线性加速度，包括车轮旋转的影响，与运动方向相反，并且为

$a'_{f}={\cfrac {\mu 'g\left(1-{\cfrac {Nm}{M}}\right)\cos \theta }{\alpha _{R}}}={\cfrac {\mu 'g\alpha _{m}\cos \theta }{\alpha _{R}}}\,}$,

其中车轮质量因子 $\alpha _{w}$ 已被定义为

$\alpha _{w}=1-{\frac {Nm}{M}}\,$.

由于这是一个恒定加速度，它可以在运动方程中写成一个有效减少的重力。到目前为止，所有几何、旋转和滑动摩擦效应的减少重力为

$g'_{\theta f}=g{\cfrac {\sin \theta -\mu '\alpha _{w}\cos \theta }{\alpha _{R}}}\,$.

使用以上值，车轮到轴承的摩擦力为 0.00946 牛顿。

请注意，由于车身质量更大（137.7 克车身加上四个 1.0 克车轮），轻轮车的车轮到轴承的摩擦力比标准轮车的摩擦力大 8%。但是，使用针式轴承可以将摩擦力减少一半，一些公开级别的比赛允许使用针式轴承。1 毫米针式轴承的机械优势为 30，摩擦力为 0.00453 牛顿（假设为轻轮）。

另一个结果是，抬起的车轮不会减少车轮到轴承的摩擦力。三轮车只是将重量分配到三个轴承上而不是四个轴承上，摩擦力是相同的。所有抬起的车轮优势都来自于旋转动能。

滚动摩擦

摩擦有两种：静摩擦和动摩擦。静摩擦是静止物体所受到的阻力，例如，静止在混凝土地板上的重箱子。滚动阻力 是滚动车轮与表面之间的摩擦。它是一种静摩擦，因为即使车轮在移动，它也没有与表面滑动。动摩擦是阻碍运动物体运动的力。使用箱子为例，当您在地板上滑动箱子时，必须克服的就是这种力。在车轮的例子中，滚动阻力是静止的，而滑行 或烧胎 涉及动摩擦。从这个意义上说，滚动阻力在很大程度上对松木赛车来说是一种“良好”的摩擦，因为它所做的功很少，并且因为它有助于将本来会是滑行摩擦的摩擦转化为车轮和轴承之间明显更小的摩擦。

滚动阻力产生的力由下式给出

$F_{r}=C_{rr}N\,$

其中 C_rr 是滚动摩擦系数 (CRF)，而$N$ 是法向力（垂直于轨道）。低滚动阻力轮胎的 CRF 值约为 0.002（参见滚动阻力 文章）。

在斜率为 $\theta$ 的轨道上，法向力垂直于轨道，由下式给出

$N_{\theta }=Mg\cos \theta \,$.

然后来自滚动阻力的摩擦力为

$F_{\theta r}=C_{rr}Mg\cos \theta \,$.

该力作用在与汽车运动方向相反的方向上。由该力引起的线性加速度为

$a'_{\theta rr}=g'C_{rr}\cos \theta ={\cfrac {gC_{rr}\cos \theta }{\alpha _{R}}}\,}$,

导致有效滚动阻力降低的重力为

$g'_{\theta rr}=g{\cfrac {\sin \theta -C_{rr}\cos \theta }{\alpha _{R}}}\,$,

滚动阻力降低的重力可以代入运动方程，以求解汽车在任何时间点的距离、速度和加速度。

在平坦的路段上，$\theta =0$ 并且

$F_{r}=C_{rr}Mg=0.002\times 0.1417\,kg\times 9.807\,m/s^{2}=0.0028\,N\$.

轮轴摩擦和滚动阻力的大小相当。从上面一节，滚动阻力估计约为0.003 N，而上面估计的轮轴摩擦大约是它的三倍。

可以降低CRF的汽车改装可以将滚动阻力降低相同的倍数。例如，“V”或“H”胎面花纹限制了车轮与轨道之间的接触面积，从而降低了CRF和滚动阻力。需要注意的是，抬高的车轮不会降低整体滚动阻力，因为汽车的全部重量分布在剩余的三个车轮上，并增加了它们的滚动阻力。然而，后轮驱动的汽车的后轮的滚动阻力更大，因为它们承受了更大的重量比例。

带摩擦的运动

包括轨道几何形状、车轮旋转、滑动摩擦和滚动摩擦的影响的“全部”降低的重力为

$g'_{\theta fr}={\cfrac {g_{\theta fr}}{\alpha _{R}}}=g{\cfrac {\sin \theta -\mu '\alpha _{w}\cos \theta -C_{rr}\cos \theta }{\alpha _{R}}}\,$.

注意，降低的重力可能是负数。特别是，当 $\theta =0$ 时，它在平坦的轨道上是负数。另一个有趣的现象是，$\theta$ 将存在一个最小值，低于该值，汽车将永远无法克服摩擦力并开始滚动——即使在倾斜的轨道上！

运动方程变为

$a(t)=g'_{\theta fr}\,;\,v(t)=g'_{\theta fr}t+v_{0}\,;\,d(t)={\cfrac {1}{2}}g'_{\theta fr}t^{2}+v_{0}t+d_{0}\,$.

比赛开始时，$v_{0}=0$ 和 $d_{0}=0$。当到达平坦路段的起点时，只需将时间重置为零，并使用 $\theta =0$，$v_{0}=v_{max}$（您必须根据这些方程式计算 $v_{max}$） 和 $d_{0}=L_{r}$。

测量摩擦力

可以使用图 1 中的装置测量静摩擦力和动摩擦力。^[3] 从 牛顿第二运动定律，我们知道力是平衡的，因此法向力平衡了汽车上的重力。

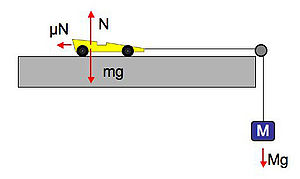图 1. 测量平坦表面上的摩擦系数。

$N_{f}=mg\,$.

当质量 M 恰好平衡静摩擦力时

$\mu N_{f}=mg\,$

以及

$\mu =M/m\,$ .

图 2. 测量倾斜表面上的摩擦系数。

读者可以验证，在图 2 所示的倾斜情况下，摩擦系数由以下公式给出

$\mu ={\frac {\left({\frac {M}{m}}-\sin(\theta )\right)}{\cos(\theta )}}\,$.

可以使用上述任何一种装置来确定动摩擦力，但操作过程需要更多耐心。增加或减少质量 M，直到在推动汽车时，汽车以恒定速度运动。此时，重力等于动摩擦力。诀窍是汽车不能加速也不能减速；我们希望 F=ma=0，但这次汽车是在运动中。

空气阻力

气体或液体对物体的摩擦力称为 阻力，阻力 F_d 可以通过以下公式计算。^[4]

$\mathbf {F} _{d}={1 \over 2}\rho AC_{d}v^{2}=bv^{2}$

其中 ρ 是空气密度（约为 1.2 kg/m³），v 是空气相对于物体的速度，A 是物体的正面面积，C_d 是 阻力系数，它取决于车辆的形状和表面（但对于典型的汽车，大约为 0.4）。常数 b 在上面定义为一个约定。对于一辆松木赛车，A 取决于汽车的设计——未切割的木块为 0.0014 m²。对于一辆使用标准车轮的 5 盎司的汽车，其速度为 4.75 m/s，产生的阻力为 0.0081 N。使用 $F=ma$，我们得到加速度为 -0.057 kgm/$s^{2}$，约为重力的 0.6%，但这仍然足以使汽车在赛道平坦路段的减速从 4.75 m/s 降至 4.69 m/s。^[5] 类似赛道的数值积分表明，比赛时间慢了 1.8%。^[6] 实际上，所有汽车都会受到一定的空气阻力，但低矮流畅的设计可能比空气动力学较差的汽车快几百分之一秒。

在松木赛车的尺寸和速度下，空气的 粘度完全无关紧要；唯一重要的空气阻力是阻力，它与空气密度和速度的平方成正比。阻力是一种 冲击压力。

要得到受冲击压力阻力影响的车辆的运动方程，我们考虑一辆在倾斜轨道上行驶的汽车，其车轮旋转并受到摩擦力，并在此模型中加入空气阻力。根据力的平衡，汽车的加速度为以下公式

${\frac {\mathbf {F} _{d}}{M}}=a(t)={\cfrac {g_{\theta fr}-{\frac {b}{M}}v^{2}}{\alpha _{R}}}$,

回顾一下，力与加速度通过牛顿第二运动定律有关，加速度是速度的导数。因此，运动速度方程可以写成

这是一个关于速度的非线性微分方程。它的解并不直接，但可以求解。运动方程为

$a(t)=g'_{\theta fr}\left[1-\tanh ^{2}\left(t{\sqrt {\cfrac {g'_{\theta fr}b}{\alpha _{R}M}}}\right)\right]\,$,

$v(t)={\sqrt {\frac {g'_{\theta fr}\alpha _{R}M}{b}}}\tanh \left(t{\sqrt {\cfrac {g'_{\theta fr}b}{\alpha _{R}M}}}\right)\,$,

$d(t)={\frac {\alpha _{R}M}{b}}\ln \left[\cosh \left(t{\sqrt {\cfrac {g'_{\theta fr}b}{\alpha _{R}M}}}\right)\right]\,$.

摩擦学

石墨的分子结构。碳原子是形成六边形平面结构的灰色球体。这些平面可以很容易地相互滑动，使块状石墨变得光滑。

摩擦学是研究摩擦、润滑和磨损的学科。由于摩擦是减缓松木赛车速度的力，而润滑可以减少摩擦，因此摩擦学是这项运动中必不可少的科学。磨损不是一个重要的考虑因素，因为正如我们在上面看到的那样，力很小。润滑剂必须减少车轮和轴之间的摩擦，并且必须与聚苯乙烯车轮相容。膨胀的聚苯乙烯被称为泡沫塑料，是热可可的绝佳杯子，但却是装有机溶剂（如汽油或萘，问问你爸爸关于旧汽车修理店的技巧）的糟糕容器。纯聚苯乙烯可以交联，与聚丁二烯形成共聚物，被称为高抗冲聚苯乙烯 (HIPS) 或高抗冲塑料。HIPS 非常适合注塑成型，因此松木赛车车轮使用它并不偶然。尽管如此，仍应注意防止不合适的溶剂，润滑剂、油漆或清洁剂远离车轮。润滑的另一个考虑因素是可能会用过量的润滑剂（尤其是液体）弄脏赛道。出于这个原因，一些比赛规则只允许使用干粉润滑剂。

二硫化钼 (MoS₂) 的 X 射线晶体结构。钼是蓝色，硫是黄色。

石墨

石墨，与钻石一样，是碳的几种形式之一。与钻石不同，石墨是一种劣质宝石，但它是一种极好的润滑剂。这是因为钻石中的化学键形成三维结构，而石墨中的化学键形成二维结构。石墨的二维片材可以轻松地相互滑动，使石墨粉末具有润滑特性。

二硫化钼

二硫化钼的化学式为 MoS₂，其化学结构与石墨类似，因为它形成了相互滑动的二维层。在松木赛车的应用中，二硫化钼粉末通常与石墨粉末混合。

特氟龙

特氟龙是杜邦公司对聚四氟乙烯 (PTFE) 的品牌名称，它是一种合成的氟聚合物（一种含有氟的聚合物）。特氟龙具有所有已知固体材料中最低的摩擦系数。它以粉末形式用作松木赛车润滑剂。