现代物理学/相对性原理应用

相对论在波中的应用

回到波的相位，我们立即看到

\phi =\mathbf {k} \cdot \mathbf {x} -\omega t=\mathbf {k} \cdot \mathbf {x} -(\omega /c)(ct)={\underline {k}}\cdot {\underline {x}}.

因此，写波的一个简洁方法是 $A({\underline {x}})=\sin({\underline {k}}\cdot {\underline {x}}).$ (6.8)

由于 ${\underline {x}}$ 已知是四维向量，并且波的相位已知是独立于参考系的标量，因此可以得出结论， ${\underline {k}}$ 确实是四维向量，而不仅仅是一组数字。因此，波四维向量长度的平方也必须是一个独立于参考系的标量

{\underline {k}}\cdot {\underline {k}}=\mathbf {k} \cdot \mathbf {k} -\omega ^{2}/c^{2}=const.

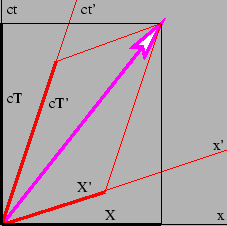
Figure 5.2: Resolution of a four-vector into components in two different reference frames.

四维向量在两个不同参考系中分解为分量的示意图。

让我们仔细回顾一下这意味着什么。正如该图所示，我们可以将位置四维向量 *x* 分解到两个不同参考系的坐标系中，例如 ( *X*, *T* ) 和 ( *X′*, *T′* )，但这只是表示同一个向量的不同方法。

这与三维向量在旋转坐标系中具有不同分量的方式完全相同。

类似地，就像三维向量在所有坐标系中具有相同的幅度一样，四维向量也是如此；即

X^{2}-c^{2}T^{2}=X^{\prime 2}-c^{2}T^{\prime 2}

将此应用于波四维向量，我们可以推断出

k^{2}-c^{-2}\omega ^{2}=k^{\prime 2}-c^{-2}\omega ^{\prime 2}

其中 *k* 和 ω 的无标注和带标注值分别指的是波四维向量在两个不同参考系中的分量。

到目前为止，这个论点适用于任何波。但是，波可以分为两类，一类是存在 *特殊* 参考系的波，另一类是不存在这种特殊参考系的波。

例如，声波在承载声音的气体静止的参考系中看起来最简单。同样，光在折射率不等于 1 的材料介质中传播也是如此。在这两种情况下，只有在材料介质静止的坐标系中，波速在所有方向上都是相同的。

如果没有材料介质，那么就没有明确的方法找到一个特殊坐标系，因此这些波必须属于第二类。这包括真空中所有的波，例如光。

在这种情况下，可以进行以下论证。一个相对于频率为 ω 且波数为 *k* 的波运动的观察者看到频率为 ω′ 且波数为 *k′* 的波。如果观察者能够以任何方式判断这些波是否来自一个相对于它们运动的源，那么他们就可以利用这一点来识别这些波的特殊坐标系，因此这些波看起来应该就像来自一个静止的频率为 ω 的源。

这迫使我们得出结论，对于这样的波

\omega ^{2}=c^{2}k^{2}+\mu ^{2}\,

其中 μ 是一个常数。所有在真空中传播的波都必须满足这个形式，这是一个比经典物理学中更加受限的选择。