信号处理/数字滤波器

数字滤波器

数字滤波器本质上是采样系统。输入和输出信号由时间距离相等的样本表示。

有限脉冲响应 (FIR) 滤波器

有限脉冲响应 (FIR) 滤波器的特点是，时间响应仅取决于输入信号的给定数量的最后一个样本。换句话说：一旦输入信号降至零，滤波器输出将在给定数量的采样周期后也降至零。

输出 $y(k)$ 由最后一个输入样本的线性组合给出 $x(k-i)$ .

y(k)=\sum _{i=0}^{N-1}b(i)\cdot x(k-i)

系数 $b(i)$ 给出了组合的权重。它们还对应于 z 域滤波器传递函数的分子系数。

下图显示了一个阶数为 $N$ 的 FIR 滤波器

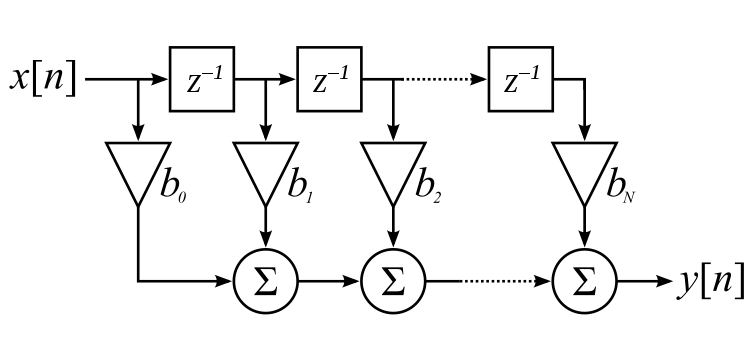
对于线性相位滤波器，系数值围绕中间系数对称，并且可以将延迟线折叠回该中间点以减少乘法次数。

FIR 滤波器的传递函数只包含分子。这对应于全零滤波器。

FIR 滤波器通常需要高阶，通常达到数百。因此，选择这种滤波器将需要大量的硬件或 CPU。尽管如此，选择 FIR 滤波器实现的一个原因是能够实现线性相位响应，这在某些情况下可能是一个要求。然而，滤波器设计者可以选择 IIR 滤波器，在通带中具有良好的相位线性，例如贝塞尔滤波器，或者设计一个全通滤波器来校正标准 IIR 滤波器的相位响应。

平均滤波器

顾名思义，平均滤波器（或简单移动平均滤波器，SMA 滤波器）计算信号的最后一个 $N$ 个样本的平均值

y(k)={\frac {1}{N}}\cdot \sum _{i=0}^{N-1}x(k-i)

它是 FIR 滤波器的最简单形式，所有系数都相等。

平均滤波器的传递函数由下式给出

{\begin{aligned}H(z)&={\frac {1}{N}}\cdot \sum _{i=0}^{N-1}z^{-i}\\&={\frac {1}{N}}\cdot \left({\frac {1-z^{-N}}{1-z^{-1}}}\right)\end{aligned}}

平均滤波器的传递函数在频域上有 $N$ 个等间距的零点。但是，直流处的零点被滤波器的极点掩盖了。因此，在直流处有一个更大的瓣，它代表了滤波器的通带。

加权移动平均

加权移动平均滤波器给样本添加权重，以便对其中一些样本给予更多重视。

y(k)={\frac {\sum _{i=0}^{N-1}w(k-i)\cdot x(k-i)}{\sum _{i=0}^{N-1}w(k-i)}}

权重可以线性变化或指数变化。

递归实现

移动平均滤波器的递归实现基于这样一个事实，即两个连续输出样本的输出由相同的一组输入样本的总和构成，只是第一个和最后一个样本除外。

y(k)=y(k-1)+{\frac {1}{N}}\cdot [x(k)-x(k-(N-1))]

级联积分梳状 (CIC) 实现

级联积分梳状滤波器 (CIC) 是一种特殊的技术，用于实现串联放置的平均滤波器。平均滤波器的串联放置增强了直流处的第一个瓣，相对于所有其他瓣。

CIC 滤波器实现了 $N$ 个平均滤波器的传递函数，每个滤波器计算 $RM$ 个样本的平均值。因此，它的传递函数由下式给出：

H(z)=\left({\frac {1-z^{-R\cdot M}}{1-z^{-1}}}\right)^{N}

CIC 滤波器用于将信号样本数量减少 R 倍，或者换句话说，以较低的频率对信号进行重新采样，丢弃 R-1 个样本中的 R 个样本。因子 M 指示信号使用了第一个瓣的多少部分。平均滤波级数 N 指示其他频段被抑制的程度，以牺牲在直流附近的传输函数不太平坦为代价。

CIC 结构允许仅使用加法器和寄存器来实现整个系统，而不使用任何在硬件方面贪婪的乘法器。

R 倍的下采样允许将信号分辨率提高 log₂(R) 位。

IIR 滤波器

典型滤波器

典型滤波器使用与滤波器阶数相等的延迟元件数量来实现滤波器传输函数，每个分子系数一个乘法器，每个分母系数一个乘法器，以及一系列加法器。类似于有源滤波器的典型结构，这种类型的电路已被证明对元件值非常敏感：系数的微小变化会对传输函数产生很大影响。

这里也是如此，有源滤波器设计已从典型滤波器转移到其他结构，例如“二阶节链”或“蛙跳滤波器”。

二阶节链

“二阶节”，通常称为“双二阶”，实现二阶传输函数。滤波器的传输函数可以分解为传输函数的乘积，每个传输函数都与一对极点和可能的一对零点相关联。如果传输函数的阶数为奇数，则必须在链中添加一个一阶节。该节与实极点和可能存在的实零点相关联。

最著名的滤波器双二阶结构是

直接形式 1
直接形式 2
直接形式 1 转置
直接形式 2 转置

下图所示的直接形式 2 转置在所需硬件以及信号和系数量化方面特别有趣。

数字蛙跳滤波器

滤波器结构

数字蛙跳滤波器基于对模拟有源蛙跳滤波器的模拟。这种选择的动机是为了继承原始梯形电路的优异通带灵敏度特性。

以下 4 阶全极点低通蛙跳滤波器

可以通过将模拟积分器替换为累加器来实现为数字电路。

将模拟积分器替换为累加器对应于将 Z 变换简化为 z = 1 + sT，它们是泰勒级数中 z = exp(sT) 的前两个项。对于采样频率远高于信号带宽的滤波器，这种近似足够好。

传输函数

上述滤波器的状态空间表示可以写成

{\begin{array}{ccrcccccc}z\cdot {\begin{bmatrix}w_{1}\\w_{2}\\w_{3}\\w_{4}\end{bmatrix}}&=&{\begin{bmatrix}1-{\frac {T}{t_{1}}}&-{\frac {T}{t_{1}}}&0&0\\{\frac {T}{t_{2}}}&1&-{\frac {T}{t_{2}}}&0\\0&{\frac {T}{t_{3}}}&1&-{\frac {T}{t_{3}}}\\0&0&{\frac {T}{t_{4}}}&1-{\frac {T}{t_{4}}}\end{bmatrix}}&\cdot &{\begin{bmatrix}w_{1}\\w_{2}\\w_{3}\\w_{4}\end{bmatrix}}&+&{\begin{bmatrix}{\frac {T}{t_{1}}}\\0\\0\\0\end{bmatrix}}&\cdot &U_{in}\\U_{out}&=&{\begin{bmatrix}0&0&0&1\end{bmatrix}}&\cdot &{\begin{bmatrix}w_{1}\\w_{2}\\w_{3}\\w_{4}\end{bmatrix}}&+&{\begin{bmatrix}0\end{bmatrix}}&\cdot &U_{in}\end{array}}

从这个方程组可以写出 A、B、C、D 矩阵：

A={\begin{bmatrix}1-{\frac {T}{t_{1}}}&-{\frac {T}{t_{1}}}&0&0\\{\frac {T}{t_{2}}}&1&-{\frac {T}{t_{2}}}&0\\0&{\frac {T}{t_{3}}}&1&-{\frac {T}{t_{3}}}\\0&0&{\frac {T}{t_{4}}}&1-{\frac {T}{t_{4}}}\end{bmatrix}}

B={\begin{bmatrix}{\frac {T}{t_{1}}}\\0\\0\\0\end{bmatrix}}

C={\begin{bmatrix}0&0&0&1\end{bmatrix}}

D={\begin{bmatrix}0\end{bmatrix}}

有了这个表示，就可以使用像 Octave 或 Matlab 这样的信号处理工具来绘制滤波器的频率响应或检查其零点和极点。

在数字跳跃滤波器中，系数的相对值决定了传递函数的形状（巴特沃斯，切比雪夫，…），而它们的幅度则决定了截止频率。将所有系数除以 2 会使截止频率降低一个倍频程（也是 2 倍）。

一个特例是巴特沃斯 3 阶滤波器，其时间常数的相对值为 1、1/2 和 1。因此，这个滤波器可以在硬件中实现，无需任何乘法器，而使用移位代替。

自回归滤波器 (AR)

自回归 (AR) 模型是以下形式的处理模型

u(n)=\sum _{m=1}^{M}a^{*}(m)u(n-m)+x(n)

其中u(n)是模型的输出，x(n)是模型的输入，u(n - m)是模型输出值的先前样本。这些滤波器被称为“自回归”，因为输出值是基于先前输出值的回归来计算的。AR 过程可以用全极点滤波器来表示。

ARMA 滤波器

自回归移动平均 (ARMA) 滤波器是 AR 和 MA 滤波器的组合。滤波器的输出作为加权输入样本和加权输出样本的线性组合给出

y(n)=\sum _{m=0}^{M}a^{*}(m)x(n-m)+\sum _{k=1}^{K}b^{*}(k)y(n-k)

ARMA 过程可以被认为是数字 IIR 滤波器，具有极点和零点。

Yule-Walker 方程

AR 滤波器在许多情况下是首选，因为它们可以使用Yule-Walker 方程进行分析。另一方面，MA 和 ARMA 过程可以通过复杂的非线性方程进行分析，这些方程难以研究和建模。

如果我们有一个具有抽头权重系数a（a(n), a(n - 1), ... 的向量）的 AR 过程，输入为x(n)，输出为y(n)，我们可以使用 Yule-Walker 方程。我们说 σ_x² 是输入信号的方差。我们把输入数据信号视为随机信号，即使它是确定性信号，因为我们不知道它的值，直到我们收到它。我们可以将 Yule-Walker 方程表示为

[Yule-Walker 方程]