材料强度/应力状态

工程力学中的材料强度

(最后) →

主应力

一般的应力状态可以用一个对称的 3 x 3 矩阵来表示。

总是可以找到一个坐标系，使得所有的剪切应力都为零。然后，3 x 3 矩阵被对角化，对角线上是三个主应力，所有其他分量都等于零。三个主应力通常标记为σ₁、σ₂和σ₃。
σ₁ 是最大的 (拉伸最大的) 主应力，σ₃ 是最小的 (压缩最大的) 主应力，σ₂ 是中间的主应力。

应力不变量

$I_{1}=\sigma _{3}+\sigma _{2}+\sigma _{1}$

$I_{2}=\sigma _{1}\sigma _{2}+\sigma _{2}\sigma _{3}+\sigma _{3}\sigma _{1}$

$I_{3}=\sigma _{1}\sigma _{2}\sigma _{3}$

静水应力

所谓的静水应力 σ_h 由下式给出

$\sigma _{h}=\left.{\frac {\sigma _{1}+\sigma _{2}+\sigma _{3}}{3}}\right.$

偏应力

正应力 - 压力

where pressure = average stress

莫尔圆

考虑二维应力状态，其中应力为σ_x、σ_y和τ_xy。我们有，对于另一个与x-y 成θ角的正交轴系 x'-y' ，应力为

$\sigma _{x'}={\frac {\sigma _{x}+\sigma _{y}}{2}}+{\frac {\sigma _{x}-\sigma _{y}}{2}}\cos 2\theta +\tau \sin 2\theta$

$\tau _{x'y'}=-{\frac {\sigma _{x}-\sigma _{y}}{2}}\sin 2\theta +\tau _{xy}\cos 2\theta$

从上面的公式可以看出，对于由σ_x、σ_y和τ_xy 给定的任何应力状态，我们都可以找到一个θ值，使得σ_x'的值最大。这个值称为主应力σ₁（对于最大值）或σ₂（对于最小值）。

主应力由下式给出

$\sigma _{1,2}={\frac {\sigma _{x}+\sigma _{y}}{2}}\pm {\sqrt {\left({\frac {\sigma _{x}-\sigma _{y}}{2}}\right)^{2}+\tau _{xy}^{2}}}$

最大剪切应力由下式给出：

τ_max = (σ₁ − σ₂)/2

根据σ_x'和τ_x'y'的定义，我们有：

$\left(\sigma _{x'}-{\frac {\sigma _{x}+\sigma _{y}}{2}}\right)^{2}+\tau _{x'y'}^{2}=\left({\frac {\sigma _{x}-\sigma _{y}}{2}}\right)^{2}+\tau _{xy}^{2}$

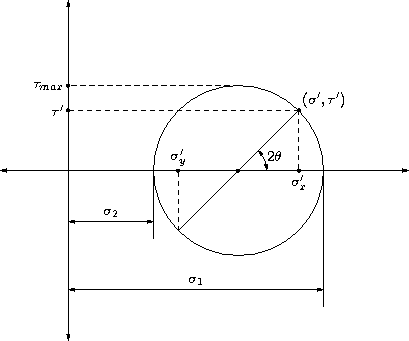
在σ-τ图中，这是一个圆，圆心位于x轴上，圆心到原点的距离由(σ_x + σ_y)/2给出，半径由下式给出：

$R={\sqrt {\left({\frac {\sigma _{x}-\sigma _{y}}{2}}\right)^{2}+\tau _{xy}^{2}}}$

该圆被称为莫尔圆，它有助于可视化一点处的应力状态。

上图显示了应力状态(σ, τ)的莫尔圆。圆心和半径由上述公式给出。另一个应力σ_y可以通过与(σ, τ)点相对的点读出。任何平面上的应力可以通过简单的几何结构找到。

常见情况下的莫尔圆

在这种情况下，上述剪切应力为σ₁/2。

液体，根据定义，不能承受剪切力。因此，莫尔圆图只是一个点。（这个点应该位于轴的负侧，因为液体只能抵抗压缩）

对于纯剪切，莫尔圆的圆心位于原点。

失效准则

对于各向同性材料，物体上任意一点的应力状态完全由主应力三元组确定。

现在我们能够变换应力得到主应力，我们可以使用这些应力来考虑一些假设用于在双轴和三轴应力状态下材料失效的准则（理论），这些准则通常基于在单轴应力状态下材料屈服和断裂的实验。根据这些实验，失效类型取决于材料类型。延性材料（大多数金属）的失效发生在达到弹性极限并开始屈服时。非延性材料（例如铸铁、混凝土）的失效发生在脆性断裂。

最大剪切应力准则

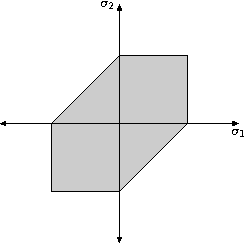
对于延性材料，一种失效理论是最大剪切应力理论。我们知道最大剪切应力由τ_max = (σ₁ − σ₂)/2给出。屈服强度σ_y可以通过单轴拉伸试验确定。因此，如果最大剪切应力理论有效，则当最大剪切应力达到σ_y/2时发生失效。

在上图中，如果应力状态位于阴影区域之外，则材料会失效。

最大畸变能准则

如果最大剪切应力理论有效，则当最大剪切应力达到 ${\frac {{\sqrt {2}}\sigma _{y}}{3}}$ 时发生失效。

材料失效

每种材料的实际失效模式都是唯一的，尽管可以将某些准则应用于材料类别。 失效模式。疲劳失效，