材料力学/扭转

工程力学中的材料力学

作用在长杆上的扭矩会使其沿扭矩方向扭转。分析是在垂直于轴线的截面上进行的，内阻扭矩的总和等于作用在系统上的外部扭矩。在本章中研究的杆件将做出以下假设

我们想要找到由于施加扭矩T而在半径为c的圆形轴中产生的最大剪切应力τ_max。根据上述假设，我们有，在轴内的任何点r处，剪切应力为τ_r = r/c τ_max。

∫τ_rdA r = T

∫ r²/c τ_max dA = T

τ_max/c∫r² dA = T

现在，我们知道，

J = ∫ r² dA

是横截面积的极惯性矩。

因此，最大剪切应力

τ_max = Tc/J

上述方程称为扭转公式。

现在，对于实心圆轴，我们有，

J = π/32(d)⁴

此外，对于任何距轴心r距离的点，我们有，剪切应力τ由下式给出

τ = Tr/J

在本分析中，我们只考虑简单圆轴的扭转荷载，即圆柱或无裂缝的非偏心管。圆轴在机械中作为传递扭矩的部件最为常见，例如旋转部件的传动轴（如电机传动轴）。这是幸运的，因为非圆形杆件在扭转下的分析很难进行解析。

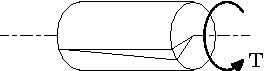
上图显示了一个在某一端受到扭矩T作用的轴的扭转。我们知道剪切角γ由下式给出

γ = τ/G

对于半径为c的轴，我们有

φ c = γ L

其中L是轴的长度。现在，τ由下式给出

τ = Tc/J

因此

φ = TL/GJ

作用在轴线x点上的扭矩T_x作用的圆形轴的扭转角φ由下式给出

$\phi =\phi _{B}-\phi _{A}=\int _{A}^{B}{\frac {T_{x}}{J_{x}G}}dx$

其中J_x是截面x处的矩。请注意，只要圆轴是圆形的，就可以使用扭转公式来计算面积变化缓慢的轴。