材料力学/入门概念

工程力学中的材料力学

应力

应力被定义为平均力除以力作用的物体面积。更准确地说，我们可以谈论一点的应力，或者简称为应力，这是当面积（一个无限小面积dA）接近于零时的极限情况。由于作用在无限小面积上的无限小力的法向分量而产生法向应力，而由于作用在无限小面积上的无限小力的切向分量而产生剪切应力。（注意：严格地说，应力并不存在。伸长率（ $\epsilon$ ) 和刚度 (E) 才存在。应力是一种方便的数学结构，它允许轻松地操作公式。）

考虑一个作用在任何任意角度上的微元面积 dA 上的力 dF。τ_xx = dF_x/dA 是法向应力，也表示为σ_x。剪切应力由τ_xy = dF_y/dA 和τ_xz = dF_z/dA 给出，其中 dF_y 和 dF_z 分别是力 dF 的 y 和 z 分量。这些剪切应力在平面y-z 上。

现在，不是考虑无限小的面积，而是考虑所讨论点处的无限小的体积。设这个体积是一个以dx、dy 和dz 为边的平行六面体。在这种情况下，一般来说有九个非零应力。它们形成一个应力张量，用以下 3x3 矩阵表示。

$\left({\begin{matrix}\sigma _{x}&\tau _{xy}&\tau _{xz}\\\tau _{yx}&\sigma _{y}&\tau _{yz}\\\tau _{zx}&\tau _{zy}&\sigma _{z}\end{matrix}}\right)$

因此，在平面应力情况下（例如，取平面x-y），我们将有四个分量的应力张量。此外，鉴于剪切应力对称性（τ_xy = τ_yx = τ），上述 3x3 矩阵简化为表示对称平面应力张量的 2x2 对称矩阵。

$\left({\begin{matrix}\sigma _{x}&\tau \\\tau &\sigma _{y}\end{matrix}}\right)$

剪切应力对称性在三维情况下成立。这使得上述 3x3 矩阵（以及相应的应力张量）是对称的：它的六个剪切应力分量中只有三个是独立的。因此，应力张量通常有六个不同的分量：三个法向应力和三个剪切应力。如上所述，在二维情况下，应力张量只有三个不同的分量：两个法向应力和一个剪切应力。

假设物体处于平衡状态，并分别在x 和y 方向受到f_x 和f_y（每单位体积）的力作用。那么可以证明，应力平衡方程在笛卡尔坐标系中的形式为

${\frac {\partial \sigma _{x}}{\partial x}}+{\frac {\partial \tau }{\partial y}}=f_{x}$

${\frac {\partial \tau }{\partial x}}+{\frac {\partial \sigma _{y}}{\partial y}}=f_{y}$

因此，在平面应力情况下，我们有两个方程涉及三个未知数。

现在转向一个最简单的物体一维载荷的例子。考虑一根两端沿纵轴拉伸的杆。

如果我们取一个垂直于轴线的截面，很容易看出σ_x = P/A，其中P 是载荷，A 是截面的横截面积。

现在考虑横截面相对于纵轴倾斜θ 的情况。在这种情况下，我们可以将力P 分解到沿截面和垂直于截面的方向。力的分量分别为P cosθ 和P sinθ。横截面的面积现在为A / cosθ。法向应力为σ_θ = P cosθ/(A/ cosθ) = (P/A) cos²θ。类似地，剪切应力为τ_θ = (P/A) sinθ cosθ。

应变

材料的应变定义为尺寸变化量与原始尺寸之比，是一个无量纲量。它用符号 ε 表示，其中 ε = (L − L₀)/L₀。这里 L₀ 称为标距长度。

上述定义的应变称为工程应变或名义应变，不同于自然应变或真应变，其定义为

$\epsilon _{n}=\int _{L_{0}}^{L}{\frac {dL'}{L'}}=\ln \left({\frac {L}{L_{0}}}\right)=\ln(1+\epsilon )$

请注意，对于较小的 ε 值，工程应变和自然应变是相同的，而且就本书中所述的大多数载荷和位移而言，其差异并不重要。此外，使用符号 e 表示工程应变和符号 ε 表示真应变的做法并不罕见。

在无穷小的情况下，我们有应变 ε_x = du/dx，其中 du 是线段 dx 的长度变化。因此，总长度变化由 Δ = ∫₀^L du = ∫₀^L ε_x dx 给出。

胡克定律

胡克定律指出，对于某些材料，应力与应变呈线性关系。这是罗伯特·胡克发现的经验定律，他在弹簧上观察到这种行为。因此，对于一维情况，我们有：

$\sigma =E\epsilon$

其中 E 是称为杨氏模量的比例常数。请注意，我们认为 E 的值在所有方向上都是相同的。其性质在各个方向上没有方向变化的材料称为各向同性材料。在不同方向上具有不同性质的材料称为各向异性。各向异性的最常见原因是材料的晶体性质。但是，大多数常见的结构材料在较大范围内没有相同的晶体取向。各向异性的另一个原因是材料加工的方式。一些加工方式，例如拉拔，往往会在特定方向上产生应力。

将胡克定律应用于长度变化的定义，我们有：

$\Delta =\int _{0}^{L}{\frac {\sigma }{E}}dx=\int _{0}^{L}{\frac {P}{AE}}dx$

或者：

$\Delta ={\frac {PL}{AE}}$

从力学中我们知道，弹簧的伸长量与力呈线性关系，比例常数通常用 k 表示。因此，轴向载荷作用下梁的弹簧常数为 AE/L。这可以扩展到不同形状的部件，因此结构是按复杂方式排列的弹簧的组合体。

泊松比

在许多材料中，纵向应变与横向应变呈线性关系。横向应变与纵向应变之比称为泊松比，用 ν 表示。

$\nu =-{\frac {\epsilon _{lat}}{\epsilon _{long}}}$

泊松比的值因材料而异，大多数常见金属约为 0.30。

近年来，再入材料的发现引起了极大的兴趣。这些是具有负泊松比的独特蜂窝和泡沫。三维各向同性固体中泊松比的允许范围为 -1 到 1/2（尽管一些聚合物泡沫已被发现表现出 1.0 的值）。

温度影响

材料由于温度变化而改变长度。为了量化该值，长度和温度必须参考某个确定的温度。变化率由线性热膨胀系数量化，用变量 CoF & α 表示，根据应变定义，我们有 ε = α ΔT，其中 ΔT 是温度变化（与给定参考点相比）。如果我们在刚性支撑之间有一个结构构件，则该构件内会产生 ΔT 的应变。还存在相关的应力，称为热应力，但是对于由于温度变化而改变长度但不受约束的构件，不会产生应力。横截面由不同 CoF 的材料组成的结构构件，会带来一个更复杂的问题。

由于变形而储存的能量

当压缩一根杆时，对杆所做的功将以能量的形式储存起来。在上图中，储存的能量显示为阴影区域。现在，我们知道，对于弹簧常数为 k、伸长量为 x 的弹簧，其储存的能量为 1/2 k x²。对于一根杆，其常数为 AE/L、伸长量为 PL/AE，其储存的能量为 1/2 P²L / AE。从上述公式可以看出，对于相同的直径和材料，使用长螺栓比短螺栓好，因为长螺栓的峰值载荷 P 更低，而无需进行任何动力学分析。

弹性变形和塑性变形

到目前为止，我们已经考虑了在施加载荷时发生弹性变形的构件。其中一些符合胡克定律，因此应力与应变之间的关系是线性的。弹性变形是指材料在外部载荷去除后能够恢复其原始形状的能力。但是，我们知道，对于较大的载荷，材料的变形是永久性的，这称为塑性变形。能够进行塑性变形的金属称为延性材料。无法进行塑性变形的材料称为脆性材料。

弹性区域非常小的材料称为塑性材料。上图显示了这种材料的理想化。当达到一定的应力状态时，材料会流动。

能够承受较大变形并保持弹性的材料被称为弹性材料。上图显示了一种理想的弹性材料——在这种情况下，它也遵循胡克定律，被称为线性弹性材料。需要注意的是，一种物质可以是弹性的，但仍然不遵循胡克定律（非线性弹性）。

大多数金属在小载荷下会发生弹性变形，在更大载荷下会发生塑性变形。对于大多数金属来说，当材料发生塑性变形时，应力会有一定的增加。然而，上面所示的弹塑性近似对于简单的分析来说已经足够了。

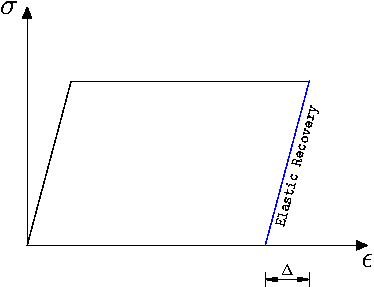
需要注意的是，表现出这种行为的材料会显示出所谓的弹性恢复，即样品会表现出一定的恢复到之前状态的趋势。在上图中，在载荷移除后，恢复量为Δ。注意，在卸载状态下，材料存在残余变形。

有些材料在塑性流动过程中表现出应力增加，这种现象被称为应变硬化。在这种情况下，可以使用具有两个斜率的应力应变曲线来近似模拟它们，但这种分析在实际应用中很少使用，因为大多数结构变形发生在弹性区域，塑性流动很可能被认为是失效模式。

剪切应变和模量

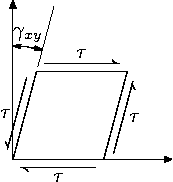
之前我们介绍了材料在轴向载荷作用下的应力-应变关系，我们发现应力σ与应变ε成正比。如果我们将剪切应力τ与剪切应变γ作图，对于遵循胡克定律的材料，我们将得到一条直线。因此，胡克定律可以使用以下方程扩展到剪切应力：τ = Gγ，其中G是剪切模量，γ是剪切应变。