| 糟糕。我应该从这些图中删除 alpha beta 和 gamma |
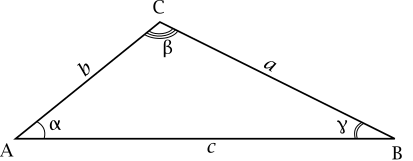
对于任何顶点为  的三角形,对应角为
的三角形,对应角为  ,对应对边长为
,对应对边长为  ,正弦定理指出
,正弦定理指出

这些表达式中的每一个都等于三角形 外接圆(过点  的圆)的直径。该定理也可以用倒数表示
的圆)的直径。该定理也可以用倒数表示


从顶点  向
向  (或
(或  的延长线)作垂线
的延长线)作垂线  ,将该三角形分为两个直角三角形
,将该三角形分为两个直角三角形  和
和  。我们可以用两种不同的方法计算高
。我们可以用两种不同的方法计算高  的长度
的长度 
 ;
;
 .
.
- 从这两个等式中消去

 .
.

通过使用另外两个垂直线,可以证明正弦定理。证毕。
这个公式可以用来在知道一条边和三个角的情况下求解三角形的另外两条边。 (如果知道两个角,则第三个角很容易求得,因为三个角的和是  .) 查看 已知 ASA 求解三角形。 它也可以用来在知道两条边和其中一条边所对的角的情况下求解一个角。
.) 查看 已知 ASA 求解三角形。 它也可以用来在知道两条边和其中一条边所对的角的情况下求解一个角。
三角形的面积可以用多种方法求解。 如果知道三条边,则使用海伦公式。
如果知道两条边和夹角,请参考上图中的第二个图。 假设边  和
和  ,以及它们之间的夹角
,以及它们之间的夹角  已知。 术语 /alpha 和 /gamma 是由希腊字母表示的变量,它们在三角学中通常可以互换使用,就像英文变量 x、y、z、a、b、c 等。 从三角形
已知。 术语 /alpha 和 /gamma 是由希腊字母表示的变量,它们在三角学中通常可以互换使用,就像英文变量 x、y、z、a、b、c 等。 从三角形  , 高度
, 高度  是
是  所以面积是
所以面积是  。
。
如果知道两个角和夹边,请参考上图中的第二个图。 假设边  和角
和角  和
和  已知。 假设
已知。 假设  。 那么
。 那么

因此
 .
.




























