 模函数
模函数模函数写成  ,它的定义是
,它的定义是  。你也可以写成
。你也可以写成  ,因为二次方会把任何负数变成正数,然后你取平方根,函数就变回原来的函数。模函数是多对一映射,因此没有逆函数。模函数用于当结果的值很重要而符号不重要时。只有在英国英语中才使用“模函数”这个词,否则它被称为绝对值函数。因此,在大多数计算器上你会看到 abs()。
,因为二次方会把任何负数变成正数,然后你取平方根,函数就变回原来的函数。模函数是多对一映射,因此没有逆函数。模函数用于当结果的值很重要而符号不重要时。只有在英国英语中才使用“模函数”这个词,否则它被称为绝对值函数。因此,在大多数计算器上你会看到 abs()。
在求解包含模的不等式时,重要的是要记住你不能简单地忽略模。相反,你需要使用规则: 。然后像你解决一般问题一样解决它。例如
。然后像你解决一般问题一样解决它。例如
求解 x 



在  图中,图像的负半部分关于 x 轴翻转。下面是
图中,图像的负半部分关于 x 轴翻转。下面是  的图像。
的图像。

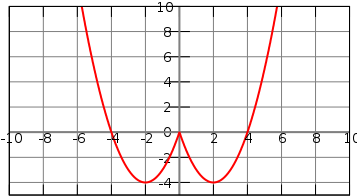
在  图中,图像的正半部分关于 y 轴翻转。下面是
图中,图像的正半部分关于 y 轴翻转。下面是  的图像。
的图像。

以 e 为底的指数函数是一个由无穷级数定义的超越函数,其近似值为 2.71828。
 .
.
e 是数学中最重要的数字之一,因为它被用于大多数自然增长过程的计算。由于它是一个指数函数,因此它遵循所有指数函数的定律。自然指数是自然对数的逆函数,因此  。右侧是
。右侧是  的图像。
的图像。
自然对数是以 e 为底的对数函数: 。它有一个特殊的符号
。它有一个特殊的符号  。由于自然对数是一个对数函数,因此它遵循所有对数函数的定律。自然对数是自然指数的逆函数,因此
。由于自然对数是一个对数函数,因此它遵循所有对数函数的定律。自然对数是自然指数的逆函数,因此  。右侧是
。右侧是  的图像。
的图像。
自然函数的主要用途之一是计算自然增长或衰减,可以使用以下公式计算: ,其中 y(t) 是最终值,
,其中 y(t) 是最终值, 是初始值,k 是增长常数,t 是经过的时间。一种特殊的衰变是元素的半衰期,其中 k 定义为:
是初始值,k 是增长常数,t 是经过的时间。一种特殊的衰变是元素的半衰期,其中 k 定义为: 。指数增长和衰减在从测量细菌菌落生长到计算涉及利息的应用中都有非常广泛的应用。
。指数增长和衰减在从测量细菌菌落生长到计算涉及利息的应用中都有非常广泛的应用。
一个细菌菌落开始时有 200 个细菌,2 小时后菌落增长到 600 个细菌。预测 6 小时后菌落中细菌的数量?
由此我们知道
- y(t) = 600
 = 200
= 200- k = x
- t = 2
现在我们将这些值代入公式

现在我们确保 e 是单独的

由于 ln 是反函数,我们用它来去除底数 e。

现在我们可以解出 x。
 ,所以菌落的增长因子约为 0.55
,所以菌落的增长因子约为 0.55
现在我们可以预测 6 小时后细菌的数量。


碳-14 元素的半衰期为 5730 年。100 克 C-14 样本何时会减少到 20% 的 C-14 和 80% 的 C-12?
- y(t) = 20% * 100 = 20
 = 100
= 100- half-life = 5730
- t = x
我们将所有已知数代入函数。请注意增长常数的特殊公式。

现在我们确保 e 是单独的

由于 ln 是反函数,我们用它来去除底数 e。


现在我们重新排列等式以隔离 t。

解出 t,我们得到该样本将在大约 13304.6 年后减少到 20% 的 C-14 和 80% 的 C-12。

在核心 3 中,我们将变换表补充了三个反射。以下是完整的变换表。
 是
是  关于 x 轴的反射。
关于 x 轴的反射。 是
是  关于 y 轴的反射。
关于 y 轴的反射。 是
是  当 y < 0 时关于 x 轴的反射。
当 y < 0 时关于 x 轴的反射。 是
是  当 x > 0 时关于 y 轴的反射。
当 x > 0 时关于 y 轴的反射。 是
是  关于直线 y=x 的反射。
关于直线 y=x 的反射。  必须具有 1:1 映射。
必须具有 1:1 映射。
 当
当  时,远离 y 轴拉伸;当
时,远离 y 轴拉伸;当  时,朝向 y 轴拉伸。在这两种情况下,变化量为 1/b 个单位。
时,朝向 y 轴拉伸。在这两种情况下,变化量为 1/b 个单位。 当
当  时,它会沿着 x 轴方向被拉伸;当
时,它会沿着 x 轴方向被拉伸;当  时,它会沿着 x 轴方向被拉伸。在这两种情况下,变化幅度都是 a 个单位。
时,它会沿着 x 轴方向被拉伸。在这两种情况下,变化幅度都是 a 个单位。
 是 f(x) 向右平移 h 个单位的结果。
是 f(x) 向右平移 h 个单位的结果。 是 f(x) 向左平移 h 个单位的结果。
是 f(x) 向左平移 h 个单位的结果。 是 f(x) 向上平移 k 个单位的结果。
是 f(x) 向上平移 k 个单位的结果。 是 f(x) 向下平移 k 个单位的结果。
是 f(x) 向下平移 k 个单位的结果。
描述函数  如何映射到
如何映射到  。
。
1) 关于 x 轴进行反射。
2) 沿 x 轴方向拉伸 4 倍。
3) 沿 x 轴方向平移 5 个单位到左侧,也可以写成关于 x = -5 进行反射。
4) 沿 y 轴方向向上平移 10 个单位。
5) 关于 y = x 进行反射。
6) 当 y < 0 时,关于 x 轴进行反射。
7) 当 x > 0 时,关于 y 轴进行反射。
现在来看图形
 通过这些变换后的图形并不容易识别为
通过这些变换后的图形并不容易识别为  的图形。
的图形。























































