以下是处理映射问题时使用的符号。
 表示一组...。
表示一组...。
例如, 表示一组
表示一组 ,其中
,其中 大于或等于 2。
大于或等于 2。
 表示函数 f 将集合 X 映射到集合 Y。另一种写法是
表示函数 f 将集合 X 映射到集合 Y。另一种写法是  。
。
 - 自然数 - 例如,{1,2,3,. ..}
- 自然数 - 例如,{1,2,3,. ..}
 - 整数 - 例如,{...−2,−1,0,1,2,. ..}
- 整数 - 例如,{...−2,−1,0,1,2,. ..}
 - 分数(有理数)
- 分数(有理数)
 - 实数,包括有理数和无理数,但不包括复数,例如
- 实数,包括有理数和无理数,但不包括复数,例如 
无理数没有通用符号 - 它们的符号是特定的 - 例如,{ }
}
映射:连接两组项目的规则。
对象/输入:起始集合中的一个项目。
映像/输出:结束集合中的一个项目。
定义域:所有对象组成的集合。
陪域:所有可能的结束值组成的集合。
值域:陪域中实际使用的元素。
1) 唯一的 
 唯一的
唯一的  (1:1 或单射映射)
(1:1 或单射映射)
2) 若干个 
 唯一
唯一  (多对一映射)
(多对一映射)
3) 唯一 
 若干个
若干个  (一对多映射)
(一对多映射)
4) 若干个 
 若干个
若干个  (多对多映射)
(多对多映射)
注意:函数只能是一对一 (单射) 或多对一映射。
函数将每个输入值对应到唯一的输出值。如果存在两个输出值,则该公式就不是函数。例如  是函数,因为每个 x 只有一个输出值,但
是函数,因为每个 x 只有一个输出值,但  不是函数,因为每个 x 可能有两个值,例如 4 =
不是函数,因为每个 x 可能有两个值,例如 4 =  和
和  ,因此 x 可以是 2 或 -2。圆形(和类似形状)的图形代表多对多映射,因此它们不是函数。可以使用垂直线测试来确定图形是否为函数。该测试指出,当且仅当绘制的任何垂直线与图形只相交一次时,该图形才为函数。函数共有四种表示方法:
,因此 x 可以是 2 或 -2。圆形(和类似形状)的图形代表多对多映射,因此它们不是函数。可以使用垂直线测试来确定图形是否为函数。该测试指出,当且仅当绘制的任何垂直线与图形只相交一次时,该图形才为函数。函数共有四种表示方法:
1) 公式
2) 图形
3) 表格
4) 文字描述
每个函数都有定义域和值域。定义域是输入值的集合。值域是输出值的集合。请记住,如果函数存在反射或平移,则定义域和值域中的一个或两个都会存在反射或平移。例如
函数  的定义域是
的定义域是  ,值域是
,值域是  ,而函数
,而函数  的定义域是
的定义域是  ,值域是
,值域是  。参见 反射规则 1 和平移规则 2.
。参见 反射规则 1 和平移规则 2.
函数的定义域通常是所有  ,但以下三种情况除外:1) 如果 x 出现在分母中,分母为零的点不在定义域中,例如
,但以下三种情况除外:1) 如果 x 出现在分母中,分母为零的点不在定义域中,例如
 的定义域是除 1 之外的所有
的定义域是除 1 之外的所有  。
。
2) 如果指数小于零且为偶数,定义域将是  ,例如
,例如
 的定义域是
的定义域是  ,但
,但 ![{\displaystyle {\sqrt[{3}]{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a55f866116e7a86823816615dd98fcccde75473) 的定义域是所有
的定义域是所有  。
。
3) 在分段函数中,定义域会受定义的限制,例如

 的定义域将是 (5,10)。
的定义域将是 (5,10)。
对于值域,有一个简单的规则需要记住。所有偶函数的值域都是  ,奇函数的值域是所有
,奇函数的值域是所有  。
。
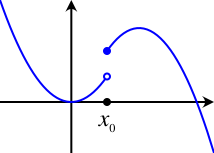
分段函数是在不同区间上由不同表达式给出的函数。  的图形如右图所示。空心圆表示该点未包含在图形中,实心圆表示该点包含在图形中。因此
的图形如右图所示。空心圆表示该点未包含在图形中,实心圆表示该点包含在图形中。因此  = 8,而不是 4。
= 8,而不是 4。
一对一函数必须对每个输入都有唯一的输出。例如, 不是一对一的,因为输入 -2 和 2 都会产生输出 4,但是
不是一对一的,因为输入 -2 和 2 都会产生输出 4,但是  是一对一的,因为每个输入都会产生唯一的输出,f(-2)= -8 且 f(2)=8。可以使用水平线测试来确定图形是否是一对一的。该测试指出,当且仅当绘制的任何水平线与图形仅相交一次时,函数才是一对一的。
是一对一的,因为每个输入都会产生唯一的输出,f(-2)= -8 且 f(2)=8。可以使用水平线测试来确定图形是否是一对一的。该测试指出,当且仅当绘制的任何水平线与图形仅相交一次时,函数才是一对一的。
函数的反函数将为函数的输出值产生输入值。函数必须是一对一的,反函数才存在。为了在数学上说明这一点: 和
和  。此外,反函数和函数的复合将产生 x:
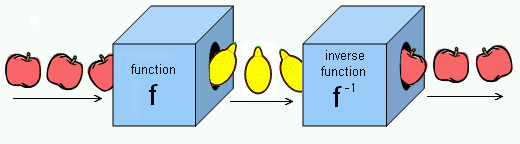
。此外,反函数和函数的复合将产生 x: 。下面可以找到一个涉及苹果和柠檬的示例。原始函数将苹果变成柠檬,而反函数将柠檬变成苹果。
。下面可以找到一个涉及苹果和柠檬的示例。原始函数将苹果变成柠檬,而反函数将柠檬变成苹果。
如何找到函数的反函数。
1) 求解关于 x 的方程
2) 将 y 与 x 交换。
3) 用  表示法写出。
表示法写出。
在例子中求  的反函数。
的反函数。
1) 

2) 
3) 
现在可以检验一下:  以及
以及  。
。
当我们画一个一一函数的反函数的图时,我们只需要交换x和y坐标: (x,y) 变为 (y,x)。坐标 (5,7) 在反函数的图上将是 (7,5)。这个图将是关于直线 y=x 的对称图形。在右侧的例子中,红色直线是  的图,绿色直线是
的图,绿色直线是 ![{\displaystyle f^{-1}\left(x\right)={\sqrt[{3}]{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b50805e63e9e51c5d9161ee0d65bb2fb9bc14474) 的图。
的图。
函数合成的数学符号是  。或者,合成也可以写成
。或者,合成也可以写成 ![{\displaystyle f\left[g\left(x\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48a7bc35b3f3b9700500700bfdd793b4bd01017c) 。当您合成两个函数时,您用第二个函数替换变量的所有实例。您可以通过合成中函数的书写顺序来判断函数的顺序
。当您合成两个函数时,您用第二个函数替换变量的所有实例。您可以通过合成中函数的书写顺序来判断函数的顺序  ,表示 F 由 G 组成。如果原始函数的定义域或值域以某种方式受限,那么复合函数也会以相同的方式受限。例如,
,表示 F 由 G 组成。如果原始函数的定义域或值域以某种方式受限,那么复合函数也会以相同的方式受限。例如, 和
和  ,求
,求  。然后找出定义域和值域。
。然后找出定义域和值域。
1) 将 f 中所有 x 的实例替换为  ,得到
,得到  。
。
2) 现在简化。  。
。
3) 定义域将是  ,因为 g(x) 永远不可能有负的 x 值,值域将是
,因为 g(x) 永远不可能有负的 x 值,值域将是  ,因为 g(x) 永远不可能为负。
,因为 g(x) 永远不可能为负。



























![{\displaystyle {\sqrt[{3}]{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a55f866116e7a86823816615dd98fcccde75473)


















![{\displaystyle f^{-1}\left(x\right)={\sqrt[{3}]{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b50805e63e9e51c5d9161ee0d65bb2fb9bc14474)

![{\displaystyle f\left[g\left(x\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48a7bc35b3f3b9700500700bfdd793b4bd01017c)








