A-level 数学/OCR/C2/三角函数

角的三角函数比

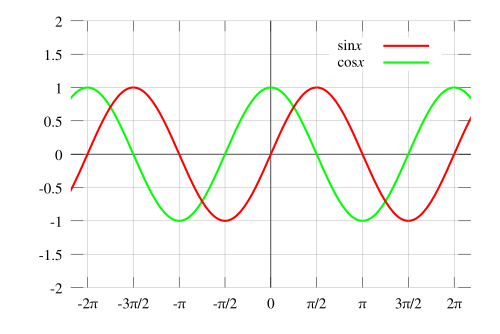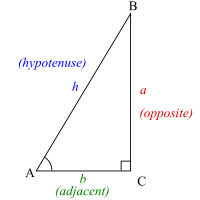
我们使用左侧的三角形来定义三个基本的三角函数比，使用角 A。一个好的记忆方法是缩略词 SOHCAHTOA，正弦对边比斜边，余弦邻边比斜边，正切对边比邻边。请记住，如果使用计算器获取三角函数比的值，请确保它处于正确的模式；如果角度是弧度，它应该处于弧度模式；如果角度是度数，它应该处于度数模式。您可以使用每个函数的倒数找到与值相对应的角度，通常列为 $\cos ^{-1},\sin ^{-1},\tan ^{-1}$ 在你的计算器上，关于反三角函数的正式讨论将在核心 3 中进行。正切图中的蓝色虚线是正切函数的渐近线。正切函数在这些点上将没有定义，因为在这些点上余弦图是零，请参阅正切恒等式。

函数	书写	定义	图
余弦	$\cos \theta \,$	${\frac {Adjacent}{Hypotenuse}}$
正弦	$\sin \theta \,$	${\frac {Opposite}{Hypotenuse}}$
正切	$\tan \theta \,$	${\frac {Opposite}{Adjacent}}$

CAST模型

CAST 模型用于显示三角函数比在哪个象限为正。一个记忆方法是 All Students Take Core 4。4 表示余弦在第四象限。另外，您需要知道 sin(x) = sin(π rad 或 180° - x) = c，cos(x) = cos(2π rad 或 360° - x) = c，tan(x) = tan(π rad 或 180° + x)= c。这很重要，因为如果 sin(x) = 1/2，并且它在 0° 和 360° 之间，那么 x 可以是 30° 或 150°。

重要的三角函数值

以下是具有常见三角函数值的表格（圆圈标有相同的值），您需要记住这些值。 $\theta \,$ $rad\,$ $\sin \theta \,$ $\cos \theta \,$ $\tan \theta \,$ $0^{\circ }$ 0 0 1 0 $30^{\circ }$ ${\frac {\pi }{6}}$ ${\frac {1}{2}}$ ${\frac {\sqrt {3}}{2}}$ ${\frac {1}{\sqrt {3}}}$ $45^{\circ }$ ${\frac {\pi }{4}}$ ${\frac {\sqrt {2}}{2}}$ ${\frac {\sqrt {2}}{2}}$ $1\,$ $60^{\circ }$ ${\frac {\pi }{3}}$ ${\frac {\sqrt {3}}{2}}$ ${\frac {1}{2}}$ ${\sqrt {3}}$ $90^{\circ }$ ${\frac {\pi }{2}}$ 1 0 无

余弦定理

勾股定理只适用于直角三角形，而余弦定理适用于任何三角形。 当你有一个直角三角形时，它会简化为与勾股定理相同的公式。 对于任何三角形 ABC，其角度测量值为 $\alpha$, $\beta$, $\gamma$ 和边长 a、b、c。

$a^{2}=b^{2}+c^{2}-2bc\cos \alpha \,$
$b^{2}=a^{2}+c^{2}-2ac\cos \beta \,$
$c^{2}=a^{2}+b^{2}-2ab\cos \gamma \,$

示例

当 a = 4 cm，b = 8 cm 且 $\gamma$ 等于 $64^{\circ }$ 时，c 的值为多少？ $c^{2}=4^{2}+8^{2}-2\times 4\times 8\cos 64^{\circ }\,$

$c^{2}=53\,$

$c\approx 7.28\ cm$

正弦定理

对于任意三角形 ABC，其角测量值为 $\alpha$，$\beta$，$\gamma$ 和边长为 a、b、c。

${\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}$

示例 如果角 α 为 $45^{\circ }$，角 β 为 $24^{\circ }$，边 b 为 3 cm，那么边 a 的长度是多少？

${\frac {a}{\sin 45^{\circ }}}={\frac {3}{\sin 24^{\circ }}}$

$a\times \sin 24^{\circ }=3\times \sin 45^{\circ }$

$a={\frac {3\times \sin 45^{\circ }}{\sin 24^{\circ }}}\approx 5.22\ {\mbox{cm}}$

三角形面积

对于任何三角形，面积等于两边乘积的一半乘以夹角的正弦值。如果夹角是直角，则公式简化为直角三角形面积公式，因为 $\sin 90^{\circ }=1$

$Area={\frac {1}{2}}bc\sin \alpha \,$

$Area={\frac {1}{2}}ac\sin \beta \,$

$Area={\frac {1}{2}}ab\sin \gamma \,$

示例

当a = 4 cm，b = 8 cm，并且 $\gamma$ 等于 $20^{\circ }$ 时，三角形的面积是多少？

$Area={\frac {1}{2}}\times 4\times 8\times \sin 20^{\circ }\,\approx 5.47\ {\mbox{cm}}^{2}$

勾股定理

$\sin ^{2}\theta +\cos ^{2}\theta =1\,$

证明

我们使用勾股定理

$a^{2}+b^{2}=c^{2}\,$

现在我们除以 $c^{2}$

${\frac {a^{2}}{c^{2}}}+{\frac {b^{2}}{c^{2}}}={\frac {c^{2}}{c^{2}}}\,$

我们得到

${\frac {a^{2}}{c^{2}}}+{\frac {b^{2}}{c^{2}}}=1\,$

我们可以写成

$\sin ^{2}\theta +\cos ^{2}\theta =1\,$

一种理解这个概念的方法是 $opposite^{2}+adjacent^{2}=hypotenuse^{2}={\frac {opposite^{2}}{hypotenuse^{2}}}+{\frac {adjacent^{2}}{hypotenuse^{2}}}=1$

实际例子

找出所有满足关系式 $15\sin ^{2}\left(x\right)=\cos \left(x\right)+13$ 的x的值， 其中 0 rad < x < 2π rad.

利用毕达哥拉斯恒等式，我们得到

$15\left(1-\cos ^{2}\left(x\right)\right)=\cos \left(x\right)+13$

现在我们可以简化

$15\cos ^{2}\left(x\right)-\cos \left(x\right)-2=0$

用 u 代替 cos(x) 更方便

$15u^{2}-u-2=0\,$

然后我们分解表达式

$\left(5u+2\right)\left(3u-1\right)=0$

$\cos \left(x\right)={\frac {-2}{5}}\ or\ {\frac {1}{3}}$

为了确定 x 的值，我们需要使用计算器上的 $\cos ^{-1}\left(x\right)$.

$\cos ^{-1}\left({\frac {-2}{5}}\right)\approx 1.9823\ rad$

$\cos ^{-1}\left({\frac {1}{3}}\right)\approx 1.2310\ rad$

但我们需要记住，在 2π 区间内，余弦函数在 2π - x 中的值相同。

2π rad - 1.2310 rad = 5.0222 rad

2π rad - 1.9823 rad = 4.3009 rad

因此，完整的答案是 1.2310 rad，1.9823 rad，4.3009 rad 和 5.0222 rad.

正切恒等式

$\tan \theta ={\frac {\sin \theta }{\cos \theta }}$

证明

$\tan \theta ={\frac {a}{b}}$

然后我们用 c 除分子和分母

$\tan \theta ={\frac {\frac {a}{c}}{\frac {b}{c}}}$

我们可以写成

$\tan \theta ={\frac {\sin \theta }{\cos \theta }}$

示例

sin(x) = 4cos(x)，求解 sin(x) 。所有单位都是弧度。

我们两边同除以 cos x，得到恒等式

tan(x)=4

我们使用 $tan^{-1}(x)$ 来得到 x = 1.3258 弧度。

现在我们可以解出 sin(x)

sin(x) = 4cos(1.3258 弧度) = 4*.2425 弧度 = .9701 弧度。

这是 C2 (核心数学 2) 模块的一部分，来自 A-level 数学 教材。

多项式除法与因式分解 / 数列与级数 / 对数与指数 / 圆与角 / 积分

附录 A: 公式