虽然许多情况下,一个值确实可以并且确实有一个精确的表示,可以用某个函数来描述,但在许多现实世界的环境中,特别是当需要对这些值进行近似时,这种方法是有用的。例如,建筑工人可能需要一个长为  英尺的房间。但是,这个值没有用,因为大多数尺子没有
英尺的房间。但是,这个值没有用,因为大多数尺子没有  的刻度。因此,工人们需要这个长度的近似值,才能建造一个长为
的刻度。因此,工人们需要这个长度的近似值,才能建造一个长为  英尺的房间。
英尺的房间。
有些数字以前很难近似,现在仍然很难近似,但微积分使近似更容易。数值分析 子领域研究用于近似数字的算法,包括但不限于残差(值与真实值之间的偏差)、小数精度级别以及达到一定精度水平所需的程序执行次数。
虽然本节不会替代数值分析(甚至没有接近),但本节希望能介绍一些有效的算法,将值近似到令人惊讶的精度水平。
在深入本节之前,第 2.4 节已经介绍了一种使用微积分作为依据来近似函数解的方法,称为二分法。因此,使用微积分来近似值并不令人惊讶。
 图 1:函数在
图 1:函数在  处的切线很好地近似了
处的切线很好地近似了  。
。
回顾导数的定义之一:它是函数  在点
在点  处的切线的斜率。考虑函数
处的切线的斜率。考虑函数  在
在  周围的局部行为,如果
周围的局部行为,如果  很小 并且
很小 并且  很小,则切线可以很好地近似值
很小,则切线可以很好地近似值  (参见图 1)。
(参见图 1)。
证明:注意,在某个可微函数  上,
上, 处的切线方程如下:
处的切线方程如下:
(2) 
其中  是切线的方程。
是切线的方程。
如果我们尝试通过切线来获得  (真实值),并且对于所有小的
(真实值),并且对于所有小的  ,都有
,都有  ,那么
,那么  。因此,
。因此,

请注意,为了使用此技术,需要满足以下条件:
 在
在  处可微,并在
处可微,并在 ![{\displaystyle \left[\alpha ,c\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/726706c3a0d704c73b14de9870efc7b0887f1c18) 上连续。
上连续。 很小,并且
很小,并且  很小。否则,可能会出现一些非常奇怪的近似值。
很小。否则,可能会出现一些非常奇怪的近似值。 在
在 ![{\displaystyle \left[\alpha ,c\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/726706c3a0d704c73b14de9870efc7b0887f1c18) 上是 单调的。(您将在第 6.2 节中更全面地了解这一点。)
上是 单调的。(您将在第 6.2 节中更全面地了解这一点。)
如果这些条件中的任何一个不成立,那么此技术将不起作用或用处不大。
示例 3.17.1:近似  |
线性逼近的好处是,我们不需要使用更难理解的函数,而是使用线性函数来估计函数的值,这可以说是我们所能使用的最简单的计算方法,假设导数的值很容易找到。
请注意,对于任何使用切线逼近(与线性逼近相同)获得的逼近,都存在一个余项,它将使逼近等于我们可以从函数中获得的真实值。 也就是说,
(3) 
其中  是余项。 不幸的是,这并不能让我们对残差进行精确估计,尤其是在我们无法找到该项的确切值的情况下。 虽然有一种技术可以确定这种类型估计的残差的上限,但将在第 6.11 节中进行,时间还很早。
是余项。 不幸的是,这并不能让我们对残差进行精确估计,尤其是在我们无法找到该项的确切值的情况下。 虽然有一种技术可以确定这种类型估计的残差的上限,但将在第 6.11 节中进行,时间还很早。
目前,我们最好的解决方案是确定我们给出的估计值低于还是高于真实值,这可以通过以下技术来完成。
高于或低于切线逼近的真实值
- 如果
 在
在  和
和  之间的区间内是凹向下的,则逼近将是一个过高估计。
之间的区间内是凹向下的,则逼近将是一个过高估计。
- 如果
 在
在  和
和  之间的区间内是凹向上的,则逼近将是一个过低估计。
之间的区间内是凹向上的,则逼近将是一个过低估计。
理由:假设  是
是 ![{\displaystyle \left[\alpha ,c\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/726706c3a0d704c73b14de9870efc7b0887f1c18) 中的二次可微函数,并且
中的二次可微函数,并且  。
。
- 情况 1(A): 假设
 且
且  ,其中
,其中 ![{\displaystyle x_{0}\in \left[\alpha ,c\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ac083804e04a47eed50ad2e6a6dd83b5e7727a2) 。那么,在
。那么,在  的切线
的切线  斜率为正,且
斜率为正,且  (见图 1 中的底部函数)。
(见图 1 中的底部函数)。
- 情况 1(B): 假设
 且
且  ,其中
,其中 ![{\displaystyle x_{0}\in \left[\alpha ,c\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ac083804e04a47eed50ad2e6a6dd83b5e7727a2) 。那么,在
。那么,在  的切线
的切线  斜率为正,且
斜率为正,且  。
。
- 情况 2(A): 设
 且
且  对
对 ![{\displaystyle x_{0}\in \left[\alpha ,c\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ac083804e04a47eed50ad2e6a6dd83b5e7727a2) 成立。那么,在
成立。那么,在  的切线,
的切线,  的斜率为负,且
的斜率为负,且  .
.
- 情况 2(B): 设
 且
且  对
对 ![{\displaystyle x_{0}\in \left[\alpha ,c\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ac083804e04a47eed50ad2e6a6dd83b5e7727a2) 成立。那么,在
成立。那么,在  的切线,
的切线,  的斜率为负,且
的斜率为负,且  (参见 图 1 中的底部函数)。
(参见 图 1 中的底部函数)。
由于向下凹函数无论切线斜率如何,都有  ,而向上凹函数无论切线斜率如何,都有
,而向上凹函数无论切线斜率如何,都有  ,我们已经证明了我们想要证明的内容。
,我们已经证明了我们想要证明的内容。 
例 3.17.2:  是高估还是低估? |
虽然线性(或切线)逼近是一种强大且易于使用的工具,可用于逼近函数,但它也存在问题。这些问题在介绍该技术时就已暗示过。每个问题都将强调为什么该工具可能并不总是非常有用。
示例 3.17.3:使用切线逼近逼近 ![{\displaystyle {\sqrt[{3}]{0.01}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7ae7406069685b769e3e766e1ff48c327b53777) |
例 3.17.4:使用切线逼近来逼近  |
因为这将在第 6.2 节中更全面地学习,假设所有习题都具有单调函数。这个例子只是为了说明这种方法常遇到的一个常见陷阱。
虽然切线近似非常有用,但它们往往只在您知道附近的值时才有用。但是,如果不存在附近的值来帮助估计其值,那么获得所需精确值的精确估计将非常困难。
牛顿-拉夫森法(在第 3.13 节中介绍)是一种有用的方法来确定函数的零点,无论它是多项式、超越、无理数、指数等。但是,牛顿-拉夫森法也可以用来近似特定函数的值。
如果您阅读了第 3.13 节,那么您应该已经了解并证明了这个等式。
例 3.17.5:近似  。 |
例 3.17.6:近似  。 |
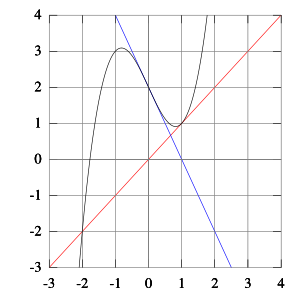 图 2:
图 2:  在
在  和
和  处的切线与
处的切线与  轴分别相交于
轴分别相交于  和
和  ,说明了为什么牛顿法对于某些起点会在这两个值之间振荡。
,说明了为什么牛顿法对于某些起点会在这两个值之间振荡。
当然,正如我们从第 3.13 节所知,牛顿-拉夫森法并不完美,在某些情况下会失效。一个明显的情况是当某个点的导数为零时。由于该导数位于分母中,一旦发生这种情况,我们就无法找到下一个可能的根。然而,还有一些其他的情况。 参考
对于某些函数,一些起点可能会进入无限循环,阻止收敛。令

并以  为起点。第一次迭代产生
为起点。第一次迭代产生  ,第二次迭代返回
,第二次迭代返回  ,因此该序列将在两者之间交替,而不会收敛到根(参见图 2)。此方程的真实解是
,因此该序列将在两者之间交替,而不会收敛到根(参见图 2)。此方程的真实解是  。在这种情况下,应该选择另一个起点。
。在这种情况下,应该选择另一个起点。
牛顿法发散的一个简单例子是求零的立方根。立方根是连续的,无限可微的,除了 ,它的导数没有定义。
,它的导数没有定义。
![{\displaystyle f(x)={\sqrt[{3}]{x}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d0572ba8a8d137d46b3aee3602d7d5b99b549ee)
对于任何迭代点 ,下一个迭代点将是
,下一个迭代点将是

该算法超过了解,落在 轴的另一侧,比最初更远;应用牛顿法实际上使每次迭代的解距离翻倍。
轴的另一侧,比最初更远;应用牛顿法实际上使每次迭代的解距离翻倍。
事实上,对于每个 ,其中
,其中 ,迭代将发散到无穷大。在极限情况下
,迭代将发散到无穷大。在极限情况下 ,迭代将在点
,迭代将在点 和
和 之间无限地交替,因此它们在这种情况下也不收敛。
之间无限地交替,因此它们在这种情况下也不收敛。
如果导数在根处不连续,则收敛可能无法在根的任何邻域内发生。考虑函数


在根的任何邻域内,该导数随着  从右侧(或左侧)逼近
从右侧(或左侧)逼近  时不断变化符号,而
时不断变化符号,而  对于
对于  成立。
成立。
因此, 在根附近是无界的,即使函数在所有地方都是可微的(因此是连续的),牛顿法几乎在根的任何邻域内都会发散,即使
在根附近是无界的,即使函数在所有地方都是可微的(因此是连续的),牛顿法几乎在根的任何邻域内都会发散,即使
- 该函数在所有地方都是可微的(因此是连续的);
- 根处的导数不为零;
 是无限可微的,除了在根处;并且
是无限可微的,除了在根处;并且- 导数在根的邻域内是有界的(与
 不同)。
不同)。
正如以下示例所示,欧拉法不像牛顿法那样快速地趋近于近似值。造成这种现象的原因有很多,但欧拉法并没有因为这个问题而失去实用价值。这些示例将展示欧拉法在何处具有实用价值。
示例 3.17.7:近似  。 |
虽然误差范围看起来很大,与  的局部线性近似值(绝对误差为
的局部线性近似值(绝对误差为  )相比,但请记住,我们的步长远大于示例 3.17 中显示的步长。如果我们选择更小的步长,那么近似值会更准确(尽管可能有点麻烦)。例如,如果步长为
)相比,但请记住,我们的步长远大于示例 3.17 中显示的步长。如果我们选择更小的步长,那么近似值会更准确(尽管可能有点麻烦)。例如,如果步长为  ,那么绝对误差将约为
,那么绝对误差将约为  。
。
 残缺
残缺
此页面或 微积分 部分是一个残缺。
你可以通过 扩展它 来帮助华夏公益教科书。























![{\displaystyle \left[\alpha ,c\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/726706c3a0d704c73b14de9870efc7b0887f1c18)




















![{\displaystyle x_{0}\in \left[\alpha ,c\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ac083804e04a47eed50ad2e6a6dd83b5e7727a2)
















![{\displaystyle {\sqrt[{3}]{0.01}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7ae7406069685b769e3e766e1ff48c327b53777)
![{\displaystyle f(x)={\sqrt[{3}]{x}}=x^{1/3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7414d427019b409754f6dd97f10b66ad34d197c6)


![{\displaystyle f^{\prime }(0)=\lim _{x\to 0}{\dfrac {\sqrt[{3}]{x}}{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e19176072715b9d5fe98a7744c58afb2f49b604)
















![{\displaystyle \left[-1,-0.8\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf7362e16de06f3383c7f2666cceb0dab91cbf9e)
![{\displaystyle x_{1},x_{2}\in \left[a,b\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6c18397bc1a9a0255326fac14c4b869c1fea9d8)































![{\displaystyle f(x)={\sqrt[{3}]{x}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d0572ba8a8d137d46b3aee3602d7d5b99b549ee)






























