微积分/定积分

假设我们给定一个函数，想要确定其图形在一个区间上的面积。我们可以猜想，但如何计算出确切的面积呢？下面，通过一些巧妙的思路，我们实际上 *定义* 这种面积，并表明通过使用所谓的 **定积分**，我们可以确切地确定曲线下的面积。

定积分的定义

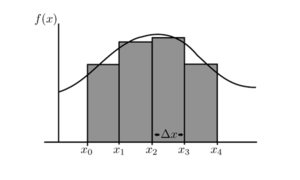图 1: $f(x)$ 从 $x=x_{0}$ 到 $x=x_{4}$ 下的曲线面积的近似值。

图 2: 从 $x_{2}$ 到 $x_{3}$ 下的曲线面积的近似矩形，采样点为 $x_{3}^{*}$ 。

定义 $f$ 图形下的面积的粗略思路是用有限个矩形来近似这个面积。由于我们可以很容易地计算出矩形的面积，因此我们得到了图形下面积的估计。如果我们使用更多更小的矩形，我们预计图形下曲线的面积会更精确，从而得到更好的近似值。在某种程度上，似乎我们可以使用我们从微分中熟悉的极限，并使用 “无限个” 矩形来得到确切的面积。让我们更详细地研究一下这样的想法。

假设我们有一个在区间 $[a,b]$ 上为正的函数 $f$，我们想找到 $f$ 在 $a$ 和 $b$ 之间的面积 $S$。让我们选择一个整数 $n$，并将区间分成 $n$ 个宽度相等的子区间（参见图 1）。由于区间 $[a,b]$ 的宽度为 $b-a$，每个子区间的宽度为 $\Delta x={\frac {b-a}{n}}$。我们用 $x_{0},x_{1},\ldots ,x_{n}$ 表示子区间的端点。这给了我们

$x_{i}=a+i\Delta x{\text{ for }}i=0,1,\dots ,n$

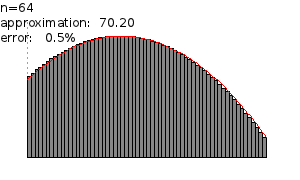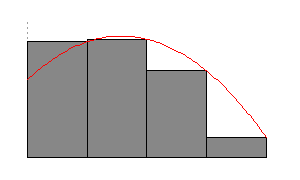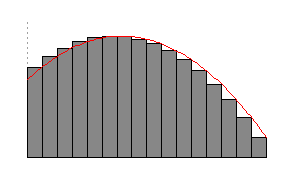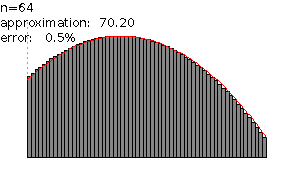图 3：黎曼和随着细分的增加，产生了更好的近似值。

现在，对于每个 $i=1,\ldots ,n$，选择区间 $[x_{i-1},x_{i}]$ 内的一个 *采样点* $x_{i}^{*}$，并考虑以 $f(x_{i}^{*})$ 为高，$\Delta x$ 为宽的矩形（参见 图 2）。这个矩形的面积是 $f(x_{i}^{*})\Delta x$。通过将所有 $i=1,\ldots ,n$ 的矩形面积加起来，我们得到面积 $S$ 的近似值。

$A_{n}=f(x_{1}^{*})\Delta x+\dots +f(x_{n}^{*})\Delta x$

使用 求和符号 来表达会更加方便。

$A_{n}=\sum _{i=1}^{n}f(x_{i}^{*})\Delta x$

对于每个数 $n$，我们得到一个不同的近似值。当 $n$ 越来越大时，矩形的宽度越来越小，从而产生更好的近似值（参见 图 3）。当 $A_{n}$ 随着 $n$ 趋于无穷大时，我们得到面积 $S$。

定积分的定义
假设$f$ 是$[a,b]$ 上的连续函数，并且$\Delta x={\frac {b-a}{n}}$ 。那么$f$ 在$a$ 和$b$ 之间的**定积分**是

$\int \limits _{a}^{b}f(x)dx=\lim _{n\to \infty }A_{n}=\lim _{n\to \infty }\sum _{i=1}^{n}f(x_{i}^{*})\Delta x$

其中$x_{i}^{*}$ 是区间$[x_{i-1},x_{i}]$ 中的任意采样点，并且$x_{k}=a+k\cdot \Delta x$ 对于$k=0,\dots ,n$ 。

事实上，如果$f$ 在$[a,b]$ 上是连续的，那么这个极限总是存在的，并且不依赖于点$x_{i}^{*}\in [x_{i-1},x_{i}]$ 的选择。例如，它们可以均匀分布，也可以在区间内以任意方式分布。这个证明是技术性的，超出了本节的范围。

符号
在考虑表达式 $\int \limits _{a}^{b}f(x)dx$（读作“从 $a$ 到 $b$ 的 $f$ 关于 $x$ 的积分 $dx$）时，函数 $f$ 被称为被积函数，区间 $[a,b]$ 为积分区间。同时 $a$ 称为积分下限，$b$ 称为积分上限。

图 4：积分表示图形下的有符号面积。

这个定义的一个重要特征是，我们也允许函数取负值。如果对于所有 $x$，有 $f(x)<0$，则 $f(x_{i}^{*})<0$，因此 $f(x_{i}^{*})\Delta x<0$。因此，$f$ 的定积分将是严格负数。更一般地，如果 $f$ 同时取正值和负值，那么 $\int \limits _{a}^{b}f(x)dx$ 将是 $f$ 图形正部分下的面积 **减去** 图形负部分之上的面积（参见 图 4）。因此，我们称 $\int \limits _{a}^{b}f(x)dx$ 是图形下的 **有符号面积**。

变量的独立性

需要注意的是，变量 $x$ 在积分定义中并没有扮演重要的角色。事实上，我们可以用任何其他字母来代替它，所以以下都是相等的

$\int \limits _{a}^{b}f(x)dx=\int \limits _{a}^{b}f(t)dt=\int \limits _{a}^{b}f(u)du=\int \limits _{a}^{b}f(w)dw$

每一个都是 $f$ 图像在 $a$ 和 $b$ 之间的有符号面积。这种变量通常被称为 哑变量 或 约束变量。

左和右黎曼和

图 5：右黎曼和

图 6：左黎曼和

以下方法有时被称为 L-RAM 和 R-RAM，RAM 代表“矩形逼近法”。

我们本可以决定选择所有的样本点 $x_{i}^{*}$ 在区间 $[x_{i-1},x_{i}]$ 的右侧（见 图 5）。然后 $x_{i}^{*}=x_{i}$ 对于所有的 $i$，我们称之为 $A_{n}$ 的面积逼近就变成了

$A_{n}=\sum _{i=1}^{n}f(x_{i})\Delta x$

这被称为 右黎曼和，而积分就是它的极限

$\int \limits _{a}^{b}f(x)dx=\lim _{n\to \infty }A_{n}=\lim _{n\to \infty }\sum _{i=1}^{n}f(x_{i})\Delta x$

或者，我们可以把每个样本点都放在区间的左侧。在这种情况下 $x_{i}^{*}=x_{i-1}$（见 图 6），逼近就变成了

$A_{n}=\sum _{i=1}^{n}f(x_{i-1})\Delta x$

那么 $f$ 的积分是

$\int \limits _{a}^{b}f(x)dx=\lim _{n\to \infty }A_{n}=\lim _{n\to \infty }\sum _{i=1}^{n}f(x_{i-1})\Delta x$

关键是，只要 $f$ 是连续的，这两个定义得到的积分结果相同。

例子

例子 1
在这个例子中，我们将计算由 $f(x)=x$ 图像所确定的曲线在 $x$ 为 0 到 1 之间的曲线下的面积。首先，我们固定一个整数 $n$ ，并将区间 $[0,1]$ 分成 $n$ 个宽度相等的子区间。因此，每个子区间的宽度为

$\Delta x={\frac {1}{n}}$

为了计算积分，我们将使用右端黎曼和。（我们也可以使用左端和，最终结果相同）。对于右端和，样本点为

$x_{i}^{*}=0+i\Delta x={\frac {i}{n}}\quad i=1,\ldots ,n$

请注意 $f(x_{i}^{*})=x_{i}^{*}={\frac {i}{n}}$ 。将此代入近似公式，得到

$A_{n}=\sum _{i=1}^{n}f(x_{i}^{*})\Delta x=\sum _{i=1}^{n}f\left({\frac {i}{n}}\right)\Delta x=\sum _{i=1}^{n}{\frac {i}{n}}\cdot {\frac {1}{n}}={\frac {1}{n^{2}}}\sum _{i=1}^{n}i$

现在我们使用 公式

$\sum _{i=1}^{n}i={\frac {n(n+1)}{2}}$

得到

$A_{n}={\frac {1}{n^{2}}}\cdot {\frac {n(n+1)}{2}}={\frac {n+1}{2n}}$

为了计算$f$ 在$0$ 和$1$ 之间的积分，我们取$n$ 趋于无穷大的极限，

$\int \limits _{0}^{1}f(x)dx=\lim _{n\to \infty }{\frac {n+1}{2n}}={\frac {1}{2}}$

例2
接下来我们将展示如何找到函数$f(x)=x^{2}$ 在$x=a$ 和$x=b$ 之间的积分。这次区间$[a,b]$ 的宽度为$b-a$，所以

$\Delta x={\frac {b-a}{n}}$

我们再次使用右黎曼和。所以我们选择的样本点是

$x_{i}^{*}=a+i\Delta x=a+{\frac {i(b-a)}{n}}$

因此

$A_{n}$	$=\sum _{i=1}^{n}f(x_{i}^{*})\Delta x$
	$=\sum _{i=1}^{n}f\left(a+{\frac {(b-a)i}{n}}\right)\Delta x$
	$={\frac {b-a}{n}}\sum _{i=1}^{n}\left(a+{\frac {(b-a)i}{n}}\right)^{2}$
	$={\frac {b-a}{n}}\sum _{i=1}^{n}\left(a^{2}+{\frac {2a(b-a)i}{n}}+{\frac {(b-a)^{2}i^{2}}{n^{2}}}\right)$

我们需要计算这个等式右边每一部分的值。对于前两部分，

$\sum _{i=1}^{n}a^{2}=a^{2}\sum _{i=1}^{n}1=na^{2}$

$\sum _{i=1}^{n}{\frac {2a(b-a)i}{n}}={\frac {2a(b-a)}{n}}\sum _{i=1}^{n}i={\frac {2a(b-a)}{n}}\cdot {\frac {n(n+1)}{2}}$

对于第三个求和，我们需要使用一个公式

$\sum _{i=1}^{n}i^{2}={\frac {n(n+1)(2n+1)}{6}}$

得到

$\sum _{i=1}^{n}{\frac {(b-a)^{2}i^{2}}{n^{2}}}={\frac {(b-a)^{2}}{n^{2}}}{\frac {n(n+1)(2n+1)}{6}}$

将它们组合起来

$A_{n}={\frac {b-a}{n}}\left(na^{2}+{\frac {2a(b-a)}{n}}\cdot {\frac {n(n+1)}{2}}+{\frac {(b-a)^{2}}{n^{2}}}{\frac {n(n+1)(2n+1)}{6}}\right)$

当 $n$ 趋于无穷大时，极限为

$\int \limits _{a}^{b}x^{2}dx$	$=(b-a)\left(a^{2}+a(b-a)+{\frac {1}{3}}(b-a)^{2}\right)$
	$=(b-a)\left(a^{2}+ab-a^{2}+{\frac {1}{3}}(b^{2}-2ab+a^{2})\right)$
	$={\frac {1}{3}}(b-a)(b^{2}+ab+a^{2})$
	$={\frac {1}{3}}(b^{3}-a^{3})$

练习

1. 使用 5 个子区间上的左、右手黎曼和，求函数 $f(x)=x^{6}$ 从 $x=0$ 到 $x=1$ 区域的上下界。

2. 使用 5 个子区间上的左、右手黎曼和，求函数 $f(x)=x^{6}$ 从 $x=1$ 到 $x=2$ 区域的上下界。

积分的基本性质

从积分的定义中，我们可以推导出一些基本性质。对于所有以下规则，假设 $f$ 和 $g$ 在 $[a,b]$ 上是连续的。

常数规则

常数规则 $\int \limits _{a}^{b}c\cdot f(x)dx=c\int \limits _{a}^{b}f(x)dx$

当 $f$ 为正数时，函数 $c\cdot f$ 在点 $x$ 处的函数高度是函数 $f$ 处的函数高度的 $c$ 倍。因此，$c\cdot f$ 在 $a$ 和 $b$ 之间的面积是 $f$ 之间面积的 $c$ 倍。我们也可以使用积分的定义，利用极限的常数规则来证明，

$\int \limits _{a}^{b}c\cdot f(x)dx=\lim _{n\to \infty }\sum _{i=1}^{n}c\cdot f(x_{i}^{*})=c\cdot \lim _{n\to \infty }\sum _{i=1}^{n}f(x_{i}^{*})=c\int \limits _{a}^{b}f(x)dx$

示例

我们在上一节中看到了

$\int \limits _{0}^{1}xdx={\frac {1}{2}}$

使用常数规则，我们可以用它来计算

$\int \limits _{0}^{1}3xdx=3\int \limits _{0}^{1}xdx=3\cdot {\frac {1}{2}}=1.5$ ,

$\int \limits _{0}^{1}-7xdx=-7\int \limits _{0}^{1}xdx=(-7)\cdot {\frac {1}{2}}=-3.5$ .

示例

我们在上一节中看到了

$\int \limits _{a}^{b}x^{2}dx={\frac {b^{3}-a^{3}}{3}}$

我们可以使用这个和常数规则来计算

$\int \limits _{1}^{3}2x^{2}dx=2\int \limits _{1}^{3}x^{2}dx=2\cdot {\frac {1}{3}}\cdot (3^{3}-1^{3})={\frac {2}{3}}(27-1)={\frac {52}{3}}$

该规则有一个用于积分常数的特殊情况。

积分常数
如果 $c$ 是常数，则 $\int \limits _{a}^{b}c\ dx=c(b-a)$

当 $c>0$ 且 $a<b$ 时，该积分是一个高度为 $c$，宽度为 $b-a$ 的矩形的面积，等于 $c(b-a)$。

示例

$\int \limits _{1}^{3}9dx=9(3-1)=9\cdot 2=18$

$\int \limits _{-2}^{6}11dx=11(6-(-2))=11\cdot 8=88$

$\int \limits _{2}^{17}0dx=0\cdot (17-2)=0$

加减法规则

积分的加减法规则
$\int \limits _{a}^{b}{\bigl (}f(x)+g(x){\bigr )}dx=\int \limits _{a}^{b}f(x)dx+\int \limits _{a}^{b}g(x)dx$

$\int \limits _{a}^{b}{\bigl (}f(x)-g(x){\bigr )}dx=\int \limits _{a}^{b}f(x)dx-\int \limits _{a}^{b}g(x)dx$

与常数规则一样，加法规则遵循极限的加法规则。

$\int \limits _{a}^{b}{\bigl (}f(x)+g(x){\bigr )}dx$	$=\lim _{n\to \infty }\sum _{i=1}^{n}{\Big (}f(x_{i}^{*})+g(x_{i}^{*}){\Big )}$
	$=\lim _{n\to \infty }\sum _{i=1}^{n}f(x_{i}^{*})+\lim _{n\to \infty }\sum _{i=1}^{n}g(x_{i}^{*})$
	$=\int \limits _{a}^{b}f(x)dx+\int \limits _{a}^{b}g(x)dx$

减法规则可以用类似的方法证明。

示例

从上面的例子中可以看出，$\int \limits _{1}^{3}9dx=18$ 以及 $\int \limits _{1}^{3}2x^{2}dx={\frac {52}{3}}$ 所以

$\int \limits _{1}^{3}(2x^{2}+9)dx=\int \limits _{1}^{3}2x^{2}dx+\int \limits _{1}^{3}9dx={\frac {52}{3}}+18={\frac {106}{3}}$

$\int \limits _{1}^{3}(2x^{2}-9)dx=\int \limits _{1}^{3}2x^{2}dx-\int \limits _{1}^{3}9dx={\frac {52}{3}}-18=-{\frac {2}{3}}$

示例

$\int \limits _{0}^{2}(4x^{2}+14)dx=4\int \limits _{0}^{2}x^{2}dx+\int \limits _{0}^{2}14dx=4\cdot {\frac {1}{3}}(2^{3}-0^{3})+2\cdot 14={\frac {32}{3}}+28={\frac {116}{3}}$

练习

3. 利用减法规则求出 $f(x)=x$ 和 $g(x)=x^{2}$ 在 $x=0$ 和 $x=1$ 之间的图形面积。

比较规则

图 7: 对 $f(x)$ 在 $[a,b]$ 上的面积进行边界划分

比较规则

• 假设对所有 $x\in [a,b]$，$f(x)\geq 0$。那么

$\int \limits _{a}^{b}f(x)dx\geq 0$

• 假设对所有 $x\in [a,b]$，$f(x)\geq g(x)$。那么

$\int \limits _{a}^{b}f(x)dx\geq \int \limits _{a}^{b}g(x)dx$

• 假设对所有 $x\in [a,b]$，$M\geq f(x)\geq m$。那么

$M(b-a)\geq \int \limits _{a}^{b}f(x)dx\geq m(b-a)$

如果 $f(x)\geq 0$，则计算 $f$ 积分的黎曼和中的每个矩形都将在 $y$ 轴上方，因此面积将是非负的。如果 $f(x)\geq g(x)$，则 $f(x)-g(x)\geq 0$，根据第一个性质，我们得到第二个性质。最后，如果 $M\geq f(x)\geq m$，则 $f$ 图像下的面积将大于高度为 $m$ 的矩形的面积，小于高度为 $M$ 的矩形的面积（参见 图 7）。所以

$M(b-a)=\int \limits _{a}^{b}M\geq \int \limits _{a}^{b}f(x)dx\geq \int \limits _{a}^{b}m=m(b-a)$

关于端点的线性

关于端点的可加性 假设 $a<c<b$。则

$\int \limits _{a}^{b}f(x)dx=\int \limits _{a}^{c}f(x)dx+\int \limits _{c}^{b}f(x)dx$

再次假设 $f$ 为正。那么这个性质应该被理解为：$f$ 图像在 $a$ 和 $b$ 之间的面积等于 $a$ 和 $c$ 之间的面积加上 $c$ 和 $b$ 之间的面积（参见 图 8）。

图 8：关于端点的可加性性质的说明

关于积分限的可加性的扩展
当 $a=b$ 时，我们有 $\Delta x={\frac {b-a}{n}}=0$ 所以

$\int \limits _{a}^{a}f(x)dx=0$

此外，在定义积分时，我们假设了 $a<b$。但是，这个定义在 $b<a$ 时也有意义，在这种情况下， $\Delta x={\frac {b-a}{n}}$ 的符号发生了变化。这使得

$\int \limits _{b}^{a}f(x)dx=-\int \limits _{a}^{b}f(x)dx$

有了这些定义，

$\int \limits _{a}^{b}f(x)dx=\int \limits _{a}^{c}f(x)dx+\int \limits _{c}^{b}f(x)dx$

无论 $a,b,c$ 的顺序如何。

练习

4. 使用练习 1 和 2 的结果以及关于端点的线性性质来确定 $\int \limits _{0}^{2}x^{6}dx$ 的上限和下限。

偶函数和奇函数

回想一下，如果函数 $f$ 满足 $f(-x)=-f(x)$，则称其为奇函数；如果满足 $f(-x)=f(x)$，则称其为偶函数。

假设 $f$ 是一个连续的奇函数，那么对于任意 $a$，

$\int \limits _{-a}^{a}f(x)dx=0$

如果 $f$ 是一个连续的偶函数，那么对于任意 $a$，

$\int \limits _{-a}^{a}f(x)dx=2\int \limits _{0}^{a}f(x)dx$

假设 $f$ 是一个奇函数，首先考虑从 $-a$ 到 $0$ 的积分。我们进行替换 $u=-x$，因此 $du=-dx$。请注意，如果 $x=-a$，那么 $u=a$；如果 $x=0$，那么 $u=0$。因此

$\int \limits _{-a}^{0}f(x)dx=-\int \limits _{a}^{0}f(-u)du=\int \limits _{0}^{a}f(-u)du$ .

由于 $f$ 是奇函数，$f(-u)=-f(u)$，因此积分变为

$\int \limits _{-a}^{0}f(x)dx=-\int \limits _{0}^{a}f(u)du$ .

现在我们可以用任何其他变量替换哑变量 $u$。因此，我们可以用字母 $x$ 替换它，得到

$\int \limits _{-a}^{0}f(x)dx=-\int \limits _{0}^{a}f(u)du=-\int \limits _{0}^{a}f(x)dx$ .

现在我们将积分分成两部分

$\int \limits _{-a}^{a}f(x)dx=\int \limits _{-a}^{0}f(x)dx+\int \limits _{0}^{a}f(x)dx=-\int \limits _{0}^{a}f(x)dx+\int \limits _{0}^{a}f(x)dx=0$ .

偶函数公式的证明类似。

5. 证明如果 $f$ 是一个连续的偶函数，那么对于任何 $a$，

$\int \limits _{-a}^{a}f(x)dx=2\int \limits _{0}^{a}f(x)dx$ .