数据科学:入门/探索性分析

首先,请在华夏公益教科书注册(并在下方列出您的用户名),以便我们了解我们的共同贡献者。此外,请遵守华夏公益教科书的编辑指南、风格手册和政策和指南。谢谢。
其次,我们每个章节只需要基本、清晰、直观的资料。我们不是试图面面俱到或完整——这本书的价值在于跨学科的简单整合。还有其他地方可以详述某个主题的深度和复杂性。在做出贡献时,请把自己放到“初学者的心态”。另外,请为每个章节确定范围,以便在一个小时的课堂时间内讲授。如果章节需要超过一个小时的授课时间,那可能过于详细。
- 在尽可能的情况下,请按照维基百科和维基词典的定义使用术语和概念。这样学生就可以参考相应的维基百科/维基词典页面,更深入地理解概念。
第三,这是一本跨学科的书。我们希望帮助人们将数据科学应用于所有领域。因此,我们需要各种各样的简单示例和简单练习。
第四,请遵守每个章节的简单结构:主要要点总结、讨论、扩展阅读、练习和参考资料。我们希望扩展阅读部分链接到在线资源。参考资料部分可能包含离线资源。要开始新页面,您应该使用来自此原型页面的维基标记。
第五,与任何华夏公益教科书一样,请随时进行更正,扩展解释,并在必要时添加内容,即使这不是“您”的章节。使用讨论页面解释可能引起争议的更改。
第六,一些语法规则
- 请将学生应该学习的关键术语和短语加粗。
- 使用“代码”标签将函数和代码片段的名称放在代码块中:
<code>lm()</code> - 使用内联链接
[[ ]]连接到维基百科、维基词典、维基共享资源、华夏公益教科书和其他维基媒体基金会属性。 - 使用参考文献(<ref> </ref>) 连接到“外部”资源——包括在线和离线资源。
- 如果您想添加图像或图表,您应该将其加载到维基共享资源中,而不是上传到华夏公益教科书中。
- 如果适用,在上传图表时添加标签
{{Created with R}})。
- 如果适用,在上传图表时添加标签
- 如果使用与R标准包不同的包,请将该包的名称用粗体括号放在每个函数后:<code>MCMCprobit()</code> ('''MCMCpack''')
- 您可以使用第三章数据的定义作为创建章节的示例。
最后,非常感谢您自愿加入我们的团队!
维基百科将探索性数据分析(EDA)定义为一种分析数据集以总结其主要特征的方法,通常使用可视化方法。在 EDA 过程中,数据科学家以开放的心态寻找数据中的模式,通常被称为“深入挖掘数据”或“亲自动手”。这种分析的结果可以导致新的假设的形成,以及进一步的数据收集活动。它还可以突出显示数据中的异常值,这些异常值可以为数据清洗活动提供信息,甚至证明数据中的系统性缺陷,这些缺陷可能使数据集无法使用。本章介绍了一些 EDA 中常用的技术。
美国数学家约翰·图基创造了 EDA 这一术语,来描述分析数据的这种方法,目的是为了提出值得检验的假设,而不是验证性数据分析,后者使用传统的统计方法来检验假设。通过从数据中获得洞察力,EDA 可以提出关于观察到的现象原因的假设,并允许数据科学家评估他们的假设,并选择合适的工具和技术进行进一步的分析。本质上,EDA 是一种以开放的心态寻找数据中模式的方法。或者正如约翰·图基所说:“如果我们需要对探索性数据分析做出简短的建议,我会建议它是态度、灵活性以及一些图表纸”(尽管如今电子表格或 R 是更容易的选择)。
有了强大的计算机和大量的统计检验,人们很容易直接深入数据集并开始分析数据,而不花时间提出正确的问题。统计学家弗朗西斯·安斯库姆(恰巧是约翰·图基的姐夫)提供了一个例子,他创建了 4 个数据集(现在被称为安斯库姆四重奏),这 4 个数据集的统计特性几乎完全相同,但当绘制图表时看起来却大不相同。
-
安斯库姆四重奏
由于 EDA 本身就是探索性的,因此在某种程度上它是一种反复试验的方法,并且哪些特定的分析被证明是有用的将取决于所调查的具体数据集。维基百科提供了一个有用的 EDA 图形技术的列表,其中一些最常用的技术概述如下。
箱线图显示了一个数值数据序列的四分位数。这些四分位数之间的间隔表明数据的离散度和偏度。在同一图表上绘制多个序列显示了序列之间的差异,而没有对它们的基本统计分布做出任何假设。
-
箱线图与 PDF
直方图是一种数据的分布图,它将每个数据点放置在一组大小相同的离散区间(或箱)中,并计算每个箱中数据点的总数。没有“最佳”的箱数,因此数据科学家可能需要对每个数据集进行试验,以找到最合适的箱宽。
-
英文字母频率(频率)
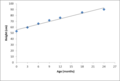
散点图用于探索两个变量之间潜在的关系,方法是在水平 X 轴上绘制一个变量,在垂直 Y 轴上绘制另一个变量。这可以暗示两个变量之间的相关性。从左下角到右上角倾斜的点模式表明正相关,而从左上角到右下角倾斜的点模式表明负相关。可以计算最佳拟合线(或“趋势线”)来评估这种相关性。对于线性相关,这被称为线性回归。
-
婴儿身高与年龄
帕累托图,以意大利经济学家维尔弗雷多·帕累托命名,是一种结合了条形图和折线图的图表,其中各个值以条形图的形式按降序排列,并叠加了累积总数作为一条线。它用于识别数据中最重要的因素。
-
帕累托图
您有权
- 共享——复制、分发、展示和表演作品(此维基中的页面)
- 混音——改编或制作衍生作品
在以下条件下
- 署名——您必须将此作品归功于华夏公益教科书。您不能暗示华夏公益教科书以任何方式认可您或您对本作品的使用。
- 相同方式共享——如果您修改、转换或基于此作品进行创作,您只能在与本许可相同或类似的许可下分发产生的作品。
- 放弃 — 只要获得版权持有人的许可,上述任何条件都可以被放弃。
- 公有领域 — 当作品或其任何元素根据适用法律属于公有领域时,此状态不受许可证的影响。
- 其他权利 — 许可证不会以任何方式影响以下任何权利
- 您的公平交易或合理使用权利,或其他适用的版权例外和限制;
- 作者的道德权利;
- 其他人可能拥有的权利,无论是作品本身还是作品的使用方式,例如宣传权或隐私权。
- 通知 — 对于任何再利用或分发,您必须向他人清楚说明此作品的许可条款。 最好的方法是链接到以下网页。