数据结构/所有章节
|
|
本作品采用知识共享 署名-相同方式共享 3.0 通用 许可协议授权。简而言之:您可以在适当署名并仅在相同、相似或兼容 许可协议下分发的条件下,共享和创作本作品的衍生作品。如果您获得版权所有者的许可,上述任何条件都可以被免除。 |
感谢使用来自维基百科 的部分内容。
计算机可以存储和处理大量数据。正式的数据结构使程序员能够在思维上将大量数据结构化为概念上易于管理的关系。
有时我们使用数据结构来让我们做更多的事情:例如,实现数据的快速搜索或排序。其他时候,我们使用数据结构来让我们做更少的事情:例如,栈的概念是更通用的数据结构的有限形式。这些限制为我们提供了保证,使我们能够更轻松地推理我们的程序。数据结构还提供有关算法复杂性的保证 - 为工作选择合适的数据结构对于编写良好的软件至关重要。
由于数据结构是更高层次的抽象,它们为我们提供了对数据组的操作,例如向列表添加项目或查找队列中优先级最高的项目。当数据结构提供操作时,我们可以将数据结构称为抽象数据类型(有时缩写为 ADT)。抽象数据类型可以最大限度地减少代码中的依赖关系,这在代码需要更改时很重要。由于您从较低级别细节中抽象出来,因此一个数据结构与另一个数据结构共享的某些更高级别共性可以用来将一个数据结构替换为另一个数据结构。
我们的编程语言配备了一组内置类型,例如整数和浮点数,这些类型使我们能够使用机器处理器具有本机支持的数据对象。这些内置类型是对处理器实际提供的类型的抽象,因为内置类型隐藏了有关其执行和限制的详细信息。
例如,当我们使用浮点数时,我们主要关心它的值以及可以应用于它的操作。考虑计算斜边的长度
let c := sqrt(a * a + b * b)
从上面生成的机器代码将使用计算这些值的通用模式并累积结果。实际上,这些模式是如此重复,以至于创建了高级语言来避免这种冗余,并允许程序员思考什么值被计算,而不是如何计算。
这里有两个有用的相关概念
- 封装是指将通用模式分组在一起,放在一个名称下,然后进行参数化,以实现对该模式的更高层次理解。例如,乘法运算需要两个源值并将这两个值的乘积写入给定的目标。该操作通过源和单个目标参数化。
- 抽象是一种机制,可以将抽象的实现细节隐藏在抽象的使用者面前。例如,当我们乘以数字时,我们不需要知道处理器实际使用的技术,我们只需要知道它的属性。
编程语言既是机器的抽象,又是封装机器内部细节的工具。例如,当编程语言足够封装用户以使其远离任何一台机器时,用编程语言编写的程序可以编译到几个不同的机器架构中。
在这本书中,我们将编程语言提供的抽象和封装更进一步:当应用程序变得更加复杂时,编程语言的抽象变得过于低级,无法有效管理。因此,我们在这些较低级别构造之上构建自己的抽象。我们甚至可以在这些抽象之上构建进一步的抽象。每次我们向上构建时,我们都会失去对较低级别实现细节的访问权限。虽然失去这种访问权限听起来可能是一笔糟糕的交易,但实际上它是一个相当不错的交易:我们主要关心的是解决手头的問題,而不是任何微不足道的决策,这些决策本来就可以任意地用其他决策来代替。当我们能够在更高层次上思考时,我们就能摆脱这些负担。
我们在这本书中涵盖的每个数据结构都可以被认为是一个单独的单元,它有一组值和一组可以用来访问或更改这些值的操作。数据结构本身可以理解为数据结构的操作集以及每个操作的属性(即,操作的作用以及我们可以预期它需要多长时间)。
大O表示法是表示计算机代码性能的一种常用方法。该表示法建立了内存中项目数量与函数的平均性能之间的关系。对于一组项目, 表示特定函数将平均对集合执行操作。 表示函数始终执行恒定数量的操作,与项目数量无关。该表示法仅表示算法复杂度,因此函数可能会执行更多操作,但 的常数倍数将被省略。
我们首先要查看的数据结构是节点结构。节点只是一个值的容器,以及指向“下一个”节点的指针(可以是null)。
以上是结构的抽象
在某些语言中,结构被称为记录或类。其他一些语言不直接支持结构,而是允许它们从其他结构(例如元组或列表)构建。
这里,我们只关心节点是否包含某种形式的值,因此我们简单地说它的类型是“元素”,因为类型并不重要。在某些编程语言中,永远不需要指定任何类型(如动态类型语言,如 Scheme、Smalltalk 或 Python)。在其他语言中,类型可能需要限制为整数或字符串(如静态类型语言,如 C)。在其他语言中,包含元素的类型的决策可以推迟到类型实际使用时(如支持泛型类型的语言,如 C++ 和 Java)。在任何这些情况下,将伪代码翻译成您自己的语言都应该比较简单。
可以很容易地实现每个指定的节点操作
// Create a new node, with v as its contained value and next as
// the value of the next pointer
function make-node(v, node next): node
let result := new node {v, next}
return result
end
// Returns the value contained in node n
function get-value(node n): element
return n.value
end
// Returns the value of node n's next pointer
function get-next(node n): node
return n.next
end
// Sets the contained value of n to be v
function set-value(node n, v)
n.value := v
end
// Sets the value of node n's next pointer to be new-next
function set-next(node n, new-next)
n.next := new-next
return new-next
end
我们主要关心的是操作和实现策略,而不是结构本身和底层实现。例如,我们更关心的是规定的时间要求,该要求指出所有操作的时间都为。以上实现满足此标准,因为每个操作所需的时间是恒定的。另一种理解恒定时间操作的方式是将它们视为其分析不依赖于任何变量的操作。(符号 在下一章中有数学定义。目前,可以安全地假设它只表示恒定时间。)
因为节点只是一个容器,既包含值,也包含指向另一个节点的指针的容器,所以节点数据结构本身(及其实现)是多么微不足道就不足为奇了。
从节点构建链
[edit | edit source]虽然节点结构很简单,但它实际上允许我们计算一些我们无法仅仅使用固定大小的整数来计算的东西。
但首先,我们将看看一个不需要使用节点的程序。以下程序将从输入流(可以来自用户或文件)中读取一系列数字,直到遇到文件末尾,然后输出最大数字和所有数字的平均值
program(input-stream in, output-stream out)
let total := 0
let count := 0
let largest :=
while has-next-integer(in):
let i := read-integer(in)
total := total + i
count := count + 1
largest := max(largest, i)
repeat
println out "Maximum: " largest
if count != 0:
println out "Average: " (total / count)
fi
end
但现在考虑解决一个类似的任务:读取一系列数字,直到遇到文件末尾,然后输出最大数字和所有能被最大数字整除的数字的平均值。这个问题有所不同,因为最大数字可能是最后输入的数字:如果我们要计算所有能被该数字整除的数字的平均值,我们需要以某种方式记住所有这些数字。我们可以使用变量来记住之前的数字,但变量只会帮助我们在输入的数字不太多的时候解决问题。
例如,假设我们要给自己 200 个变量来保存用户输入的状态。并且进一步假设每个变量都有 64 位。即使我们对我们的程序非常聪明,它也只可以计算 种不同类型的输入的结果。虽然这是一个非常大的组合数,但一个包含 300 个 64 位数字的列表需要更多的组合才能被正确编码。(一般来说,这个问题被称为需要线性空间。所有只需要有限数量变量的程序都可以用常数空间解决。)
我们可以利用节点抽象的属性,而不是构建限制编码的限制(比如只有恒定的数量的变量),从而允许我们记住计算机所能容纳的任意数量的数字
program(input-stream in, output-stream out)
let largest :=
let nodes := null
while has-next-integer(in):
let i := read-integer(in)
nodes := make-node(i, nodes) // contain the value i,
// and remember the previous numbers too
largest := max(largest, i)
repeat
println out "Maximum: " largest
// now compute the averages of all factors of largest
let total := 0
let count := 0
while nodes != null:
let j := get-value(nodes)
if j divides largest:
total := total + j
count := count + 1
fi
nodes := get-next(nodes)
repeat
if count != 0:
println out "Average: " (total / count)
fi
end
上面,如果成功读取了n个整数,将调用n次make-node。这将需要创建n个节点(这需要足够的空间来保存每个节点的值和下一个字段,加上内部内存管理开销),所以内存需求将是的量级。类似地,我们构建了这个节点链,然后再次遍历该链,这将需要步来构建链,然后还需要步来遍历它。
注意,当我们遍历链中的数字时,我们实际上是在反向查看它们。例如,假设输入到我们程序中的数字是 4、7、6、30 和 15。在遇到文件末尾后,节点链将看起来像这样
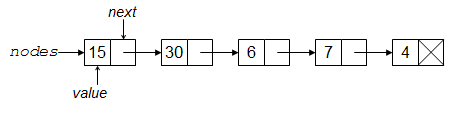
这样的链更常被称为链表。但是,我们通常更喜欢从列表或序列的角度思考,因为它们不是那么底层:链接的概念只是一个实现细节。虽然列表可以用链来创建,但在本书中,我们将介绍几种其他创建列表的方法。目前,我们更关心节点的抽象能力,而不是它的一种使用方式。
上面的算法只使用了 make-node、get-value 和 get-next 函数。如果我们使用 set-next,我们可以改变算法来生成链,使其保持原始顺序(而不是反转它)。
program (input-stream in, output-stream out)
let largest :=
let nodes := null
let tail_node := null
while has-next-integer (in):
let i := read-integer (in)
if (nodes == null)
nodes := make-node(i, null) // construct first node in the list
tail_node := nodes //there is one node in the list=> first and last are the same
else
tail_node := set-next (tail_node, make-node (i, null)) // append new node to the end of the list
largest := max(largest, i)
repeat
println out "Maximum: " largest
// now compute the averages of all factors of largest
let total := 0
let count := 0
while nodes != null:
let j := get-value(nodes)
if j divides largest:
total := total + j
count := count + 1
fi
nodes := get-next(nodes)
repeat
if count != 0:
println out "Average: " (total / count)
fi
end
归纳原理
[edit | edit source]我们可以从节点构建的链是数学归纳原理的演示
数学归纳法
|
例如,设性质 是这样的陈述:"你可以制作一个可以容纳 个数字的链条"。这是一个关于自然数的性质,因为这句话对 的特定值是有意义的。
- 你可以制作一个可以容纳 5 个数字的链条。
- 你可以制作一个可以容纳 100 个数字的链条。
- 你可以制作一个可以容纳 1,000,000 个数字的链条。
与其证明我们可以制作长度为 5、100 和一百万的链条,我们宁愿证明一般性陈述 。上面第 2 步称为 **归纳假设**;让我们证明我们可以证明它。
- 假设 成立。也就是说,我们可以制作一个包含 个元素的链条。现在我们必须证明 成立。
- 假设
chain是 元素链条的第一个节点。假设i是我们想要添加到链条中的某个数字,以制作一个长度为 的链条。 - 以下代码可以为我们实现这一点。
let bigger-chain := make-node(i, chain)
- 这里,我们有新的数字
i,它现在是bigger-chain的第一个链接所包含的值。如果chain包含 个元素,那么bigger-chain必须包含 个元素。
上面第 3 步称为 **基本情况**,让我们证明我们可以证明它。
- 我们必须证明 成立。也就是说,我们可以制作一个包含一个元素的链条。
- 以下代码可以为我们实现这一点。
let chain := make-node(i, null)
归纳法原理指出,我们已经证明可以构建一个包含 个元素的链,对于所有 的值。这是怎么回事呢?也许理解归纳法的最佳方式是将其视为创建描述无限个证明的公式的方法。在我们证明语句对于 (基本情况)为真之后,我们可以将归纳假设应用于该事实,以表明 成立。由于我们现在知道 成立,我们可以再次应用归纳假设来表明 必须成立。该原理指出,没有什么可以阻止我们反复执行此操作,因此我们应该假设它适用于所有情况。
归纳法可能听起来像一种奇怪的证明方法,但它是一种非常有用的技术。使这种技术如此有用的原因是,它可以将“证明 对所有 成立”这样看起来很困难的语句分解成两个更小、更容易证明的语句。通常情况下,基本情况很容易证明,因为它们根本不是一般性语句。大部分证明工作通常都在归纳假设中,这通常需要巧妙地重新表述语句以“附加”一个 情况的证明。
您可以将节点的包含值视为基本情况,将节点的下一个指针视为归纳假设。就像数学归纳法一样,我们可以将存储任意数量元素的难题分解成一个更简单的难题,即仅存储一个元素,然后有一个机制来附加其他元素。
归纳法求和
[edit | edit source]我们接下来考虑的归纳法的例子在本质上更具代数性
假设我们给出了公式 ,我们想证明该公式给出前 个数字的和。作为第一次尝试,我们可能会尝试仅表明这对于 1 为真
- ,
对于 2
- ,
对于 3
等等,但是我们很快就会意识到,我们的所谓证明将需要无限长的时间才能写出来!即使您完成了这个证明,并且表明它对于前十亿个数字都为真,但这并不一定意味着它对于十亿零一个或甚至一百亿也为真。这强烈暗示也许归纳法在这里会很有用。
假设我们想使用归纳法证明给定的公式确实给出了前 n 个数字的和。第一步是证明基本情况;即我们必须表明当 n = 1 时它是正确的。这相对容易;我们只需用 1 代替变量 n,我们得到 (),这表明当 n = 1 时该公式是正确的。
现在进行归纳步骤。我们必须证明如果公式对 j 成立,它对 j + 1 也成立。换句话说,假设我们已经证明了从 1 到 (j) 的总和为 ,我们想要证明从 1 到 (j+1) 的总和为 。注意这两个公式只是通过将 n 分别替换为 (j) 和 (j+1) 而来的。
为了证明这个归纳步骤,首先要注意,要计算从 1 到 j+1 的总和,你只需要计算从 1 到 j 的总和,然后加上 j+1。我们已经有了从 1 到 j 的总和的公式,当我们将 j+1 加到那个公式时,我们得到这个新公式:。所以要真正完成证明,我们只需要证明 。
我们可以通过一些简化步骤来证明上述方程成立。
渐进符号
[edit | edit source]介绍
[edit | edit source]没有一种数据结构能在所有情况下都能提供最佳性能。为了选择最适合特定任务的结构,我们需要能够判断特定解决方案的运行时间。或者,更准确地说,你需要能够判断两种解决方案的运行时间,并选择较好的一种。我们不需要知道它们会花费多少分钟和秒,但我们需要一些方法来比较不同的算法。
渐近复杂度是一种使用理想化(不可比较)的计算工作单位来表示算法成本的主要部分的方法。例如,考虑对一副牌进行排序的算法,该算法通过反复搜索牌堆中最低的牌来进行排序。该算法的渐近复杂度是牌堆中卡片数量的平方。这种二次行为是复杂度公式中的主要项,它表明,例如,如果你将牌堆的大小加倍,那么工作量将大约增加四倍。
成本的精确公式更加复杂,它包含比我们理解算法的本质复杂度所需的更多细节。对于我们的牌堆,在最坏的情况下,牌堆将从反向排序开始,因此我们的扫描必须一直进行到最后。第一次扫描将涉及扫描张牌,接下来将需要扫描张,等等。因此成本公式是。通常,用表示卡片数量,公式为,它等于。但是,项在表达式中占主导地位,这对于比较算法成本至关重要。(事实上,这是一种昂贵的算法;最佳排序算法在亚二次时间内运行。)
从渐近的角度来说,当趋于无穷大时,越来越接近纯粹的二次函数。在这样的抽象级别上,的常数因子有什么区别?因此,这种行为被称为。
现在让我们考虑如何比较两种算法的复杂度。设 是一个算法在最坏情况下,以输入大小 为函数的代价, 是另一个算法的代价函数。例如,对于排序算法, 和 将是算法在一个包含 个项目的列表上可能执行的最大步数。如果对于所有 的值, 小于或等于 ,那么复杂度函数为 的算法严格更快。但是,一般来说,我们对计算成本的关注是针对大输入的情况;因此,比较 和 对于 的较小值并不像 和 对于大于某个阈值的 的“长期”比较那么重要。
注意,我们一直在讨论算法性能的边界,而不是给出确切的速度。对我们的一副牌进行排序(使用我们的朴素二次算法)所需的实际步数将取决于牌的初始顺序。执行每一步的实际时间将取决于我们的处理器速度、处理器缓存的状态等等。在具体细节上,一切都非常复杂,而且与算法的本质无关。
O 符号
[edit | edit source]定义
[edit | edit source]O(读作“大 O”)是用来表达算法运行时间上限的正式方法。它是衡量算法完成可能需要的最长时间的一种度量。我们可以假设它代表程序的“最坏情况”。
更正式地说,对于非负函数, 和 ,如果存在一个整数 和一个常数 ,使得对于所有整数 ,,那么 是 的大 O。这表示为 。如果绘制图表, 作为您正在分析的曲线 的上限。
请注意,如果 只能取有限值(通常情况下应该如此),那么这个定义意味着存在某个常数 (可能大于 ),使得对于所有 的值, 。 的适当值是 和 的最大值。
那么,让我们举一个大 O 的例子。假设 ,以及 。我们能找到一个常数 ,使得 吗?数字 在这里有效,使我们得到 。对于任何大于 的数字 ,这仍然有效。由于我们试图将此泛化到 的较大值,而较小值 并不那么重要,我们可以说 通常比 快;也就是说, 受 约束,并且始终小于它。
然后可以说 在 时间内运行:“f-of-n 在 n 平方的时间内运行”。
为了找到上限 - Big-O 时间 - 假设我们知道 等于(精确) ,我们可以采取一些捷径。例如,我们可以从运行时间中删除所有常数;最终,在 的某个值时,它们就变得无关紧要了。这使得 。同样为了方便比较,我们删除常数乘数;在本例中为 。这使得 。也可以说 在 时间内运行;这使我们能够对估计值设定更严格(更接近)的上限。
实际示例
[edit | edit source]:将包含 个项目的列表打印到屏幕上,每个项目只看一次。
:获取一个包含 个项目的列表,反复将它分成两半,直到只剩下一个项目为止。
:获取一个包含 个项目的列表,并将每个项目与其他所有项目进行比较。
Big-Omega 符号
[edit | edit source]对于非负函数, 和 ,如果存在整数 和常数 使得对于所有整数 ,,则 是 。这记作 。
这与大O符号的定义几乎相同,只是 ,这使得 是一个下界函数,而不是上界函数。它描述了给定数据大小下 **可能发生的最佳情况**。
Theta 符号
[edit | edit source]对于非负函数, 和 , 是 的theta当且仅当 且 。这记作 。
这基本上是在说函数 在上面和下面都被同一个函数 限制。
Theta 符号用 Q 表示。
对于非负函数 和 , 是 的小 o 当且仅当 ,但 。这表示为 。
这表示 Big O 的松散边界版本。 从上面进行限制,但它没有对下面进行限制。
对于非负函数, 和 , 是 的小 omega 当且仅当 ,但是 。这表示为 .
就像小 o 一样,这是大 Omega 的等价形式。 是函数 的一个松散的下界;它从底部约束,但不是从顶部约束。
渐进符号如何与分析复杂度相关
[edit | edit source]时间比较不是算法中唯一的因素。还有空间问题。通常,在算法中会注意到时间和空间之间的权衡。渐进符号使您能够进行这种权衡。如果您将算法使用的时间和空间量视为数据随时间或空间的变化的函数(时间和空间通常分别进行分析),您可以分析在向程序中引入更多数据时如何处理时间和空间。
这在数据结构中很重要,因为您希望数据结构在处理的数据量增加时能够高效地运行。但请记住,对于大量数据高效的算法并不总是对于少量数据简单且高效的。因此,如果您知道您只处理少量数据,并且您担心速度和代码空间,那么可以对一个对于大量数据行为不佳的函数进行权衡。
渐进符号的一些例子
[edit | edit source]通常,我们使用渐进符号作为一种方便的方法来检查函数在最坏情况下或最佳情况下可能发生的情况。例如,如果您想编写一个函数,该函数搜索一个数字数组并返回最小的数字
function find-min(array a[1..n])
let j :=
for i := 1 to n:
j := min(j, a[i])
repeat
return j
end
无论数组的大小如何,每次运行find-min 时,我们都必须初始化i 和j 整数变量,并在最后返回j。因此,我们可以简单地将函数的这些部分视为常数并忽略它们。
那么,我们如何使用渐进符号来讨论find-min 函数呢?如果我们搜索一个包含 87 个元素的数组,那么for 循环会迭代 87 次,即使我们遇到的第一个元素就是最小值。同样,对于 个元素,for 循环会迭代 次。因此,我们说该函数在 时间内运行。
这个函数怎么样
function find-min-plus-max(array a[1..n]) // First, find the smallest element in the array let j := ; for i := 1 to n: j := min(j, a[i]) repeat let minim := j // Now, find the biggest element, add it to the smallest and j := ; for i := 1 to n: j := max(j, a[i]) repeat let maxim := j // return the sum of the two return minim + maxim; end
find-min-plus-max 的运行时间是多少?有两个 for 循环,每个循环迭代 次,因此运行时间显然是 。因为 是一个常数,我们可以将其丢弃并将运行时间写为 。为什么可以这样做?如果你回忆大 O 符号的定义,你正在测试其边界的函数可以乘以某个常数。如果 ,我们可以看到,如果 ,则大 O 条件成立。因此 。此规则对于各种渐近符号都是通用的。
数组是一个集合,主要包含相似的数据类型,存储在一个公共变量中。该集合形成一个数据结构,其中对象以线性方式存储,在内存中一个接一个地存储。有时数组甚至被复制到内存硬件中。
该结构也可以定义为存储带索引数据的 元素 的特定方法。数据元素在逻辑上按顺序存储在数组内的块中。每个元素都由一个 索引 或下标引用。
索引通常是一个用于寻址数组中元素的数字。例如,如果你要存储有关 8 月份每一天的信息,你需要创建一个能够寻址 31 个值的数组,每个值代表一个月中的每一天。索引规则取决于语言,但大多数语言使用 0 或 1 作为数组的第一个元素。
数组的概念对于初学者来说可能令人望而生畏,但实际上非常简单。想象一本笔记本,其页面从 1 到 12 编号。每个页面可能包含或不包含信息。笔记本就是一个 数组,包含页面。每个页面都是数组“笔记本”的 元素。在编程中,你可以通过引用页码或 下标 来检索页面上的信息,例如,notebook(4) 将引用数组笔记本中第 4 页的内容。
笔记本(数组)包含 12 页(元素)
数组也可以是多维的——与访问一维列表的元素不同,元素可以通过两个或多个索引访问,例如矩阵或张量。
多维数组与我们上面提到的笔记本示例一样简单。为了想象一个多维数组,可以想象一个日历。日历的每一页,从 1 到 12,都是一个元素,代表一个月,它包含大约 30 个元素,代表天数。每一天可能包含或不包含信息。在编程中,calendar(4,15) 将引用第 4 个月、第 15 天。因此我们得到一个二维数组。为了想象一个三维数组,可以将每一天分解成 24 个小时。现在 calendar(4,15,9) 将引用第 4 个月、第 15 天、第 9 个小时。

一个简单的 6 元素×4 元素数组
Array<Element> 操作
make-array(整数 n): Array
- 创建一个从 到 (包括)的元素索引。数组中的元素数量,也称为数组的大小,是 n。
get-value-at(Array a, 整数 index): Element
- 返回给定 index 处元素的值。index 的值必须在范围内:0 <= index <= (n - 1)。此操作也称为 下标操作。
set-value-at(Array a, 整数 index, Element new-value)
- 将数组中给定 index 处的元素设置为等于 new-value。
数组保证 常数 时间读写访问,,但是元素实例的许多查找操作(find_min、find_max、find_index)是 线性 时间,。在大多数语言中,数组非常高效,因为操作通过基于数组的基地址元素的简单公式来计算元素的地址。
数组实现因语言而异:一些语言允许自动调整数组大小,甚至包含不同类型元素(如 Perl)。其他语言则非常严格,要求在运行时知道数组的类型和长度信息(如 C)。
数组通常直接映射到计算机内存中的连续存储位置,因此它们是大多数高级语言的“自然”存储结构。
简单的线性数组是大多数其他数据结构的基础。许多语言不允许你分配除数组以外的任何结构,其他所有内容都必须在数组之上实现。唯一的例外是链表,它通常实现为单独分配的对象,但也可以在数组内实现链表。
数组索引需要是某种类型。通常,使用该语言的标准整数类型,但也有 Ada 和 Pascal 等语言允许任何离散类型作为数组索引。脚本语言通常允许任何类型作为索引(关联数组)。
边界
[edit | edit source]数组索引由具有下界和上界的取值范围组成。
在一些编程语言中,只有上界可以被选择,而下界固定为 0 (C, C++, C#, Java) 或 1 (FORTRAN 66, R).
在其他编程语言 (Ada, PL/I, Pascal) 中,上下界都可以自由选择 (甚至为负数).
边界检查
[edit | edit source]数组索引的第三个方面是检查有效范围以及访问无效索引时会发生什么。这一点非常重要,因为大多数 计算机蠕虫 和 计算机病毒 通过使用无效的数组边界进行攻击。
有三种选择
- 大多数语言 (Ada, PL/I, Pascal, Java, C#) 将检查边界,并在访问不存在的元素时引发错误条件。
- 少数语言 (C, C++) 不会检查边界,并在访问有效范围之外的元素时返回或设置一些任意值。
- 脚本语言通常在向之前无效的索引写入数据时自动扩展数组。
声明数组类型
[edit | edit source]数组类型的声明取决于特定语言中数组具有多少功能。
当语言具有固定下界和固定索引类型时,最简单的声明是。如果您需要一个数组来存储每月收入,您可以在 C 中声明
typedef double Income[12];
这为您提供了一个范围从 0 到 11 的数组。有关 C 中数组的完整描述,请参阅 C Programming/Arrays。
如果您使用的是可以同时选择下界和索引类型的语言,那么声明当然会更加复杂。以下是 Ada 中的两个示例
type Month is range 1 .. 12;
type Income is array(Month) of Float;
或者更短的
type Income is array(1 .. 12) of Float;
有关 Ada 中数组的完整描述,请参阅 Ada Programming/Types/array。
数组访问
[edit | edit source]我们通常用名称、索引在一些括号中(方括号 '[]' 或圆括号 '()')来写数组。例如,August[3]是 C 编程语言中用于引用月份中特定日期的方法。
因为 C 语言从零开始索引,August[3]是数组中的第 4 个元素。august[0]实际上指的是此数组的第一个元素。从零开始索引对于计算机来说是自然的,因为计算机对数字的内部表示从零开始,但对于人类来说,这种不自然的编号系统会导致在访问数组中的数据时出现问题。在使用基于零的索引的语言中获取元素时,请记住数组的真实长度,以免您获取了错误的数据。这是在具有固定下界的语言中编程的缺点,程序员必须始终记住“"[0]" 表示“第一个”,并在需要时添加或减去 1。具有可变下界的语言将从程序员的肩上卸下这一负担。
我们使用索引来存储相关数据。如果我们的 C 语言数组名为august,并且我们希望存储我们将在第一天去超市的信息,我们可以说,例如
august[0] = "Going to the shops today"
这样,我们就可以遍历从 0 到 30 的索引,并获得每个日期在august.
列表结构和迭代器
[edit | edit source]我们现在已经看到了两种不同的数据结构,它们允许我们存储元素的有序序列。但是,它们具有两种截然不同的接口。数组允许我们使用 get-element() 和 set-element() 函数来访问和更改元素。节点链要求我们使用 get-next() 直到找到所需的节点,然后我们可以使用 get-value() 和 set-value() 来访问和修改其值。现在,如果您编写了一些代码,然后意识到您应该使用另一个序列数据结构,会怎么样?您必须遍历您已经编写的所有代码,并将一组访问器函数更改为另一组。真麻烦!幸运的是,有一种方法可以将此更改限制在一个地方:使用List 抽象数据类型 (ADT)。
List<item-type> ADT
get-begin():List Iterator<item-type>- 返回表示列表第一个元素的列表迭代器(我们很快就会定义它)。运行时间为 。
get-end():List Iterator<item-type>- 返回表示列表最后一个元素后面的一个元素的列表迭代器。运行时间为 。
prepend(new-item:item-type)- 在列表的开头添加一个新元素。运行时间为 。
insert-after(iter:List Iterator<item-type>, new-item:item-type)- 在 iter 之后立即添加一个新元素。运行时间为 。
remove-first()- 删除列表开头的元素。运行时间为 。
remove-after(iter:List Iterator<item-type>)- 删除iter后的元素。在 时间内运行。
is-empty():Boolean- 如果列表中没有元素,则为 True。具有默认实现。在 时间内运行。
get-size():Integer- 返回列表中的元素数量。具有默认实现。在 时间内运行。
get-nth(n:Integer):item-type- 返回列表中第 n 个元素,从 0 开始计数。具有默认实现。在 时间内运行。
set-nth(n:Integer, new-value:item-type)- 将新值分配给列表中第 n 个元素,从 0 开始计数。具有默认实现。在 时间内运行。
迭代器是另一种抽象,它封装了对单个元素的访问以及在列表中进行增量移动的能力。它的接口与引言中介绍的节点接口非常相似,但由于它是一个抽象类型,不同的列表可以以不同的方式实现它。
List Iterator<item-type> ADT
get-value():item-type- 返回此迭代器所指的列表元素的值。
set-value(new-value:item-type)- 将新值分配给此迭代器所指的列表元素。
move-next()- 使此迭代器指向列表中的下一个元素。
equal(other-iter:List Iterator<item-type>):Boolean- 如果另一个迭代器指向与该迭代器相同的列表元素,则为 True。
所有操作都在 时间内运行。
List ADT 定义中还有其他几个方面需要进一步解释。首先,请注意 get-end() 操作返回一个指向列表“末尾之后”的迭代器。这使得它的实现稍微复杂一些,但允许您编写类似于以下的循环:
var iter:List Iterator := list.get-begin() while(not iter.equal(list.get-end())) # Do stuff with the iterator iter.move-next() end while
其次,每个操作都给出了最坏情况下的运行时间。任何 List ADT 的实现都保证至少能够以这种速度运行该操作。大多数实现将以更快的速度运行大多数操作。例如,List 的节点链实现可以在 时间内运行 insert-after()。
第三,一些操作说它们具有默认实现。这意味着这些操作可以用其他更基本的操作来实现。它们被包含在 ADT 中,以便某些实现能够以更快的速度实现它们。例如,get-nth() 的默认实现是在 时间内运行,因为它必须遍历第 n 个元素之前的所有元素。然而,List 的数组实现可以使用它的 get-element() 操作在 时间内实现它。其他默认实现是:
abstract type List<item-type> method is-empty() return get-begin().equal(get-end()) end method method get-size():Integer var size:Integer := 0 var iter:List Iterator<item-type> := get-begin() while(not iter.equal(get-end())) size := size+1 iter.move-next() end while return size end method helper method find-nth(n:Integer):List Iterator<item-type> if n >= get-size() error "The index is past the end of the list" end if var iter:List Iterator<item-type> := get-begin() while(n > 0) iter.move-next() n := n-1 end while return iter end method method get-nth(n:Integer):item-type return find-nth(n).get-value() end method method set-nth(n:Integer, new-value:item-type) find-nth(n).set-value(new-value) end method end type
语法糖
[edit | edit source]在这本书中,我们会不时地引入一个缩写,使我们能够编写更少的伪代码,并使您更容易阅读。现在,我们将介绍一种更简单的方法来比较迭代器,并提供一种专门用于遍历序列的循环。
我们将重载 == 运算符,而不是使用 equal() 方法来比较迭代器。确切地说,以下两个表达式是等效的:
iter1.equal(iter2) iter1 == iter2
其次,我们将使用 for 关键字来表达列表遍历。以下两个代码块是等效的:
var iter:List Iterator<item-type> := list.get-begin() while(not iter == list.get-end()) operations on iter iter.move-next() end while
for iter in list operations on iter end for
实现
[edit | edit source]为了实际使用 List ADT,我们需要编写一个具体数据类型来实现它的接口。有两个标准数据类型自然地实现了 List:引言中描述的节点链,通常称为单链表;以及数组类型的扩展,称为向量,它会自动调整大小以容纳插入的节点。
单链表
[edit | edit source]type Singly Linked List<item-type> implements List<item-type>
head 指向列表中的第一个节点。当它为 null 时,列表为空。
data head:Node<item-type>
最初,列表为空。
constructor()
head := null
end constructor
method get-begin():Sll Iterator<item-type>
return new Sll-Iterator(head)
end method
“末尾之后”的迭代器只是一个空节点。要了解原因,请考虑当您拥有指向列表中最后一个元素的迭代器并调用 move-next() 时会发生什么。
method get-end():Sll Iterator<item-type>
return new Sll-Iterator(null)
end method
method prepend(new-item:item-type)
head = make-node(new-item, head)
end method
method insert-after(iter:Sll Iterator<item-type>, new-item:item-type)
var new-node:Node<item-type> := make-node(new-item, iter.node().get-next())
iter.node.set-next(new-node)
end method
method remove-first()
head = head.get-next()
end method
这会将迭代器持有的节点指向两个节点后的节点。
method remove-after(iter:Sll Iterator<item-type>)
iter.node.set-next(iter.node.get-next().get-next())
end method
end type
如果我们想让get-size()成为一个操作,我们可以添加一个整数数据成员,它始终跟踪列表的大小。否则,默认的实现也能正常工作。
单链表的迭代器仅仅包含一个指向节点的引用。
type Sll Iterator<item-type>
data node:Node<item-type>
constructor(_node:Node<item-type>)
node := _node
end constructor
大多数操作只是传递到节点。
method get-value():item-type
return node.get-value()
end method
method set-value(new-value:item-type)
node.set-value(new-value)
end method
method move-next()
node := node.get-next()
end method
对于相等性测试,我们假设底层系统知道如何比较节点以确定相等性。在几乎所有语言中,这将是指针比较。
method equal(other-iter:List Iterator<item-type>):Boolean
return node == other-iter.node
end method
end type
向量
[edit | edit source]让我们先编写向量的迭代器。它将使向量的实现更加清晰。
type Vector Iterator<item-type>
data array:Array<item-type>
data index:Integer
constructor(my_array:Array<item-type>, my_index:Integer)
array := my_array
index := my_index
end constructor
method get-value():item-type
return array.get-element(index)
end method
method set-value(new-value:item-type)
array.set-element(index, new-value)
end method
method move-next()
index := index+1
end method
method equal(other-iter:List Iterator<item-type>):Boolean
return array==other-iter.array and index==other-iter.index
end method
end type
我们使用基本数组数据类型来实现向量。始终保持数组完全正确的大小效率低下(想想你必须进行多少次调整大小),所以我们存储了size(向量中逻辑元素的数量)和capacity(数组中的空间数量)这两个值。数组的有效索引将始终位于0到capacity-1的范围内。
type Vector<item-type> data array:Array<item-type> data size:Integer data capacity:Integer
我们用 10 的容量初始化向量。选择 10 是相当随意的。如果我们想让它看起来不那么随意,我们会选择一个 2 的幂,而像你这样的天真读者会认为,这种选择有一些深刻的、与二进制相关的理由。
constructor()
array := create-array(0, 9)
size := 0
capacity := 10
end constructor
method get-begin():Vector-Iterator<item-type>
return new Vector-Iterator(array, 0)
end method
结束迭代器的索引为size。这比最高有效索引多 1。
method get-end():List Iterator<item-type>
return new Vector-Iterator(array, size)
end method
我们将使用此方法来帮助我们实现插入例程。调用它之后,数组的capacity保证至少为new-capacity。一个简单的实现将简单地分配一个具有正好new-capacity个元素的新数组,并将旧数组复制过来。要了解为什么这是低效的,想想如果我们开始在循环中追加元素会发生什么。一旦我们超过了原始容量,每个新元素都需要我们复制整个数组。这就是为什么这个实现至少在每次需要增长时将底层数组的大小加倍。
helper method ensure-capacity(new-capacity:Integer)
如果当前容量已经足够大,则快速返回。
if capacity >= new-capacity
return
end if
现在,找到我们需要的新容量,
var allocated-capacity:Integer := max(capacity*2, new-capacity)
var new-array:Array<item-type> := create-array(0, allocated-capacity - 1)
复制旧数组,
for i in 0..size-1
new-array.set-element(i, array.get-element(i))
end for
并更新向量的状态。
array := new-array
capacity := allocated-capacity
end method
此方法使用了一个通常是非法的迭代器,该迭代器引用了向量开始之前的项目,以欺骗insert-after()做正确的事情。通过这样做,我们避免了重复代码。
method prepend(new-item:item-type)
insert-after(new Vector-Iterator(array, -1), new-item)
end method
insert-after()需要复制iter和向量末尾之间的所有元素。这意味着通常情况下,它在时间内运行。但是,在iter引用向量中的最后一个元素的特殊情况下,我们不需要复制任何元素来为新元素腾出空间。追加操作可以在时间内运行,加上ensure-capacity()调用所需的时间。ensure-capacity()有时需要复制整个数组,这需要时间。但更常见的是,它根本不需要做任何事情。
摊销分析
实际上,如果你考虑一系列追加操作,这些操作从ensure-capacity()增加向量容量的时刻开始(在此处将容量称为),并在容量下一次增加的时刻结束,你可以看到将有正好个追加操作。在容量下一次增加时,它将需要将个元素复制到新数组中。所以这整个个函数调用的序列总共进行了次操作。我们将这种在个函数调用中进行了次操作的情况称为“摊销时间”。
method insert-after(iter:Vector Iterator<item-type>, new-item:item-type)
ensure-capacity(size+1)
此循环将向量中的所有元素复制到索引高一位的位置。我们从后向前循环,以便在复制每个后续元素之前为其腾出空间。
for i in size-1 .. iter.index+1 step -1
array.set-element(i+1, array.get-element(i))
end for
现在数组中间有一个空位,我们可以将新元素放在那里。
array.set-element(iter.index+1, new-item)
并更新向量的尺寸。
size := size+1 end method
同样,也稍微作弊,以避免重复代码。
method remove-first() remove-after(new Vector-Iterator(array, -1)) end method
与insert-after()类似,remove-after需要复制iter和向量末尾之间的所有元素。因此,通常情况下,它在时间内运行。但在iter引用向量中的最后一个元素的特殊情况下,我们可以简单地将向量的尺寸减 1,而无需复制任何元素。删除最后一个元素的操作在时间内运行。
method remove-after(iter:List Iterator<item-type>)
for i in iter.index+1 .. size-2
array.set-element(i, array.get-element(i+1))
end for
size := size-1
end method
该方法有一个默认实现,但我们已经存储了大小,因此可以在 时间内实现,而不是默认的
method get-size():Integer
return size
end method
由于数组允许对元素进行常数时间访问,因此可以在 时间内实现 get- 和 set-nth(),而不是默认实现的
method get-nth(n:Integer):item-type
return array.get-element(n)
end method
method set-nth(n:Integer, new-value:item-type)
array.set-element(n, new-value)
end method
end type
双向列表
[edit | edit source]
有时我们希望 Data Structures/All Chapters 在列表中向后移动。双向列表允许列表向前和向后搜索。双向列表实现了一个额外的 迭代器 函数,move-previous()。
Bidirectional List<item-type> ADT
get-begin():Bidirectional List Iterator<item-type>- 返回表示列表第一个元素的列表迭代器(我们很快就会定义它)。运行时间为 。
get-end():Bidirectional List Iterator<item-type>- 返回表示列表最后一个元素后面的一个元素的列表迭代器。运行时间为 。
insert(iter:Bidirectional List Iterator<item-type>, new-item:item-type)- 在 iter 之前添加一个新元素。运行时间为 。
remove(iter:Bidirectional List Iterator<item-type>)- 删除 iter 指向的元素。在此调用之后,iter 将指向列表中的下一个元素。运行时间为 。
is-empty():Boolean- 如果列表中没有元素,则为真。有一个默认实现。运行时间为 。
get-size():Integer- 返回列表中的元素数量。具有默认实现。在 时间内运行。
get-nth(n:Integer):item-type- 返回列表中第 n 个元素,从 0 开始计数。具有默认实现。在 时间内运行。
set-nth(n:Integer, new-value:item-type)- 将新值分配给列表中第 n 个元素,从 0 开始计数。具有默认实现。在 时间内运行。
Bidirectional List Iterator<item-type> ADT
get-value():item-type- 返回此迭代器指向的列表元素的值。如果迭代器超过末尾,则未定义。
set-value(new-value:item-type)- 为此迭代器指向的列表元素分配一个新值。如果迭代器超过末尾,则未定义。
move-next()- 使此迭代器指向列表中的下一个元素。如果迭代器超过末尾,则未定义。
move-previous()- 使此迭代器指向列表中的前一个元素。如果迭代器指向第一个列表元素,则未定义。
equal(other-iter:List Iterator<item-type>):Boolean- 如果另一个迭代器指向与该迭代器相同的列表元素,则为真。
所有操作都在 时间内运行。
双向链表实现
[edit | edit source]
向量实现
[edit | edit source]我们已经见过的向量有一个非常合适的实现来成为一个双向列表。我们所要做的就是为它及其迭代器添加额外的成员函数;旧的函数不需要更改。
type Vector<item-type> ... # already-existing data and methods
用原始的 insert-after() 方法来实现它。该方法运行完毕后,我们必须调整 iter 的索引,以便它仍然指向同一个元素。
method insert(iter:Bidirectional List Iterator<item-type>, new-item:item-type)
insert-after(new Vector-Iterator(iter.array, iter.index-1))
iter.move-next()
end method
还可以用旧函数来实现它。remove-after() 运行完毕后,索引将已经正确。
method remove(iter:Bidirectional List Iterator<item-type>)
remove-after(new Vector-Iterator(iter.array, iter.index-1))
end method
end type
权衡
[edit | edit source]
为了选择适合工作的正确数据结构,我们需要了解我们打算对数据 *做什么*。
- 我们是否知道在任何时候都不会超过 100 个数据,或者我们需要偶尔处理千兆字节的数据?
- 我们将如何读取数据?始终按时间顺序?始终按名称排序?随机访问记录号?
- 我们是否总是将数据添加到末尾或开头?或者我们会在中间执行很多插入和删除操作?
我们必须在各种要求之间取得平衡。如果我们需要以 3 种不同的方式频繁地读取数据,请选择一个允许我们以不太慢的速度执行这 3 种操作的数据结构。不要选择一个对 *一种* 方式速度慢得无法忍受的数据结构,无论它对其他方式的速度有多快。
通常,某些任务的最短、最简单的编程解决方案将使用线性 (1D) 数组。
如果我们将数据保留为 ADT,那么可以更容易地临时切换到其他底层数据结构,并客观地衡量它是否更快或更慢。
优点/缺点
[edit | edit source]在大多数情况下,数组的优点是链表的缺点,反之亦然。
- 数组优点(相对于链表)
- 索引 - 对数组中任何元素的索引访问速度很快;链表必须从开头遍历才能到达所需元素。
- 更快 - 通常,访问数组中的元素比访问链表中的元素更快。
- 链表优点(相对于数组)
- 调整大小 - 链表可以轻松地通过添加元素来调整大小,而不会影响列表中的其他元素;数组只能通过分配新的内存块并将所有元素复制到该块来扩大。
- 插入 - 可以轻松地将元素插入到链表的中间:创建一个指向它后面的链接的新链接,并将前面的链接指向新链接。
旁注: - **如何在数组中间插入元素**。如果数组未满,您可以将要插入的数组位置或索引后的所有元素向前移动 1 位,然后插入您的元素。如果数组已满,并且您想插入元素,则需要“调整数组大小”。需要创建一个比原始数组大一个尺寸的新数组来插入您的元素,然后将原始数组的所有元素复制到新数组中,同时考虑插入元素的位置或索引,然后插入您的元素。
栈是一种基本的数据结构,在逻辑上可以认为是线性结构,用真实的物理栈或堆来表示,在这种结构中,项目的插入和删除发生在称为栈顶的一个端点。基本概念可以通过将您的数据集想象成一堆盘子或书来阐明,您只能从栈顶拿取物品来移除东西。这种结构在整个编程过程中都有使用。
栈的基本实现也称为 LIFO(后进先出),以说明它访问数据的顺序,因为正如我们将看到的,栈的实现方式有很多变化。
栈上可以执行三种基本操作。它们是 1) 将项目插入到栈中(push)。2) 从栈中删除项目(pop)。3) 显示栈的内容(peek 或 top)。
以下是一些 **栈数据类型** 通常支持的操作
Stack<item-type> 操作
push(new-item:item-type)- 将项目添加到栈顶。
top():item-type- 返回压入栈的最后一个项目。
pop()- 从栈中删除最晚压入的项目。
is-empty():Boolean- 如果不再有项目可以弹出,并且没有栈顶项目,则为真。
is-full():Boolean- 如果不再有项目可以压入,则为真。
get-size():Integer- 返回栈中元素的数量。
除了 get-size() 之外的所有操作都可以在 时间内完成。get-size() 最坏情况下运行在
基本链表实现是您可以执行的最简单的栈实现之一。从结构上来说,它是一个链表。
type Stack<item_type>
data list:Singly Linked List<item_type>
"stack follows the LIFO (last in first out) operation"
"queue follows the FIFO (first in first out) operation"
constructor()
list := new Singly-Linked-List()
end constructor
大多数操作都是通过将它们传递到底层链表来实现的。当您想将某个东西 **push** 到列表中时,您只需将其添加到链表的开头。然后,之前的顶点从添加的项目中成为“next”,并且列表的 front 指针指向新项目。
method push(new_item:item_type)
list.prepend(new_item)
end method
要查看 **top** 项目,您只需检查链表中的第一个项目。
method top():item_type
return list.get-begin().get-value()
end method
当您想将某个东西 **pop** 出列表时,只需从链表中删除第一个项目。
method pop()
list.remove-first()
end method
检查是否为空很容易。只需检查列表是否为空。
method is-empty():Boolean
return list.is-empty()
end method
检查是否已满很简单。链表被认为是无限大小的。
method is-full():Boolean
return False
end method
检查大小也会传递到列表中。
method get-size():Integer
return list.get-size()
end method
end type
发布库中的真实栈实现可能会重新实现链表,以便通过删除不需要的功能来从实现中挤出最后一滴性能。上述实现为您提供了相关想法,您可以通过内联链表代码来完成任何需要的优化。
在链表中,访问第一个元素是一个 操作。列表包含一个指针,用于检查空/满状态,如这里所做的那样,也是 (取决于做出了什么样的时间/空间权衡)。大多数情况下,栈的用户不使用 getSize() 操作,因此可以通过不优化它来节省一些空间。
由于所有操作都在栈顶进行,因此数组实现现在好得多。
public class StackArray implements Stack
{
protected int top;
protected Object[] data;
...
}
数组实现将栈底保持在数组的开头。它向数组的末尾增长。唯一的问题是,如果您在数组已满时尝试压入元素。如果是这样
Assert.pre(!isFull(),"Stack is not full.");
将失败,并抛出异常。因此,使用 Vector(参见 StackVector)来实现更有意义,因为它允许无限制增长(以偶尔的 O(n) 延迟为代价)。
复杂度
除了偶尔的 push 和 clear 之外,所有操作都是 O(1),push 和 clear 应该将所有条目替换为 null,以便它们被垃圾回收。数组实现不会替换 null 条目。Vector 实现会...

使用栈,我们可以解决许多应用,其中一些列在下面。
将十进制数转换为二进制数的逻辑如下所示
* Read a number
* Iteration (while number is greater than zero)
1. Find out the remainder after dividing the number by 2
2. Print the remainder
3. Divide the number by 2
* End the iteration
但是,这种逻辑存在问题。假设我们要找到二进制形式的数字是 23。使用这种逻辑,我们得到的结果是 11101,而不是 10111。
为了解决这个问题,我们使用栈。我们利用栈的 LIFO 属性。最初,我们将形成的二进制位 push 到栈中,而不是直接打印它。在将整个数字转换为二进制形式后,我们一次 pop 一个数字,从栈中取出并打印出来。因此,我们得到十进制数转换为正确的二进制形式。
算法
1. Create a stack
2. Enter a decimal number which has to be converted into its equivalent binary form.
3. iteration1 (while number > 0)
3.1 digit = number % 2
3.2 Push digit into the stack
3.3 If the stack is full
3.3.1 Print an error
3.3.2 Stop the algorithm
3.4 End the if condition
3.5 Divide the number by 2
4. End iteration1
5. iteration2 (while stack is not empty)
5.1 Pop digit from the stack
5.2 Print the digit
6. End iteration2
7. STOP

栈最有趣的应用之一是在解决一个名为汉诺塔的谜题中找到的。根据一个古老的婆罗门故事,宇宙的存在是根据一群和尚花费的时间来计算的,这些和尚一直在工作,将 64 个圆盘从一个柱子移动到另一个柱子上。但是,关于如何执行此操作有一些规则,即
- 您一次只能移动一个圆盘。
- 为了临时存储,可以使用第三个柱子。
- 您不能将直径更大的圆盘放在直径更小的圆盘上。[1]
这里我们假设 A 是第一个塔,B 是第二个塔,C 是第三个塔。





输出:(当有 3 个圆盘时)
令 1 为最小的圆盘,2 为中等大小的圆盘,3 为最大的圆盘。
| 移动圆盘 | 从桩 | 到桩 |
|---|---|---|
| 1 | A | C |
| 2 | A | B |
| 1 | C | B |
| 3 | A | C |
| 1 | B | A |
| 2 | B | C |
| 1 | A | C |
输出:(当有 4 个圆盘时)
| 移动圆盘 | 从桩 | 到桩 |
|---|---|---|
| 1 | A | B |
| 2 | A | C |
| 1 | B | C |
| 3 | A | B |
| 1 | C | A |
| 2 | C | B |
| 1 | A | B |
| 4 | A | C |
| 1 | B | C |
| 2 | B | A |
| 1 | C | A |
| 3 | B | C |
| 1 | A | B |
| 2 | A | C |
| 1 | B | C |
该解决方案的 C++ 代码可以用两种方法实现
这里我们假设 A 是第一个塔,B 是第二个塔,C 是第三个塔。(B 是中间塔)
void TowersofHanoi(int n, int a, int b, int c)
{
//Move top n disks from tower a to tower b, use tower c for intermediate storage.
if(n > 0)
{
TowersofHanoi(n-1, a, c, b); //recursion
cout << " Move top disk from tower " << a << " to tower " << b << endl ;
//Move n-1 disks from intermediate(b) to the source(a) back
TowersofHanoi(n-1, c, b, a); //recursion
}
}
// Global variable, tower [1:3] are three towers
arrayStack<int> tower[4];
void TowerofHanoi(int n)
{
// Preprocessor for moveAndShow.
for (int d = n; d > 0; d--) //initialize
tower[1].push(d); //add disk d to tower 1
moveAndShow(n, 1, 2, 3); /*move n disks from tower 1 to tower 3 using
tower 2 as intermediate tower*/
}
void moveAndShow(int n, int a, int b, int c)
{
// Move the top n disks from tower a to tower b showing states.
// Use tower c for intermediate storage.
if(n > 0)
{
moveAndShow(n-1, a, c, b); //recursion
int d = tower[a].top(); //move a disc from top of tower a to top of
tower[a].pop(); //tower b
tower[b].push(d);
showState(); //show state of 3 towers
moveAndShow(n-1, c, b, a); //recursion
}
}
然而,上面实现的复杂度是 O()。因此,很明显,这个问题只能针对较小的 n 值解决(通常 n <= 30)。对于僧侣来说,按照上述规则,移动 64 个圆盘所花费的步数将是 18,446,744,073,709,551,615,这无疑需要花费大量的时间!!
采用 逆波兰表示法 的计算器使用堆栈结构来保存值。表达式可以用前缀、后缀或中缀表示法表示。使用堆栈可以完成从一种表达式形式到另一种形式的转换。许多编译器使用堆栈来解析表达式、程序块等的语法,然后翻译成低级代码。大多数编程语言是 上下文无关语言,允许它们使用基于堆栈的机器进行解析。
输入 (((2 * 5) - (1 * 2)) / (9 - 7))
输出 4
分析: 五种类型的输入字符
* Opening bracket * Numbers * Operators * Closing bracket * New line character
数据结构要求: 字符堆栈
算法
1. Read one input character
2. Actions at end of each input
Opening brackets (2.1) Push into stack and then Go to step (1)
Number (2.2) Push into stack and then Go to step (1)
Operator (2.3) Push into stack and then Go to step (1)
Closing brackets (2.4) Pop it from character stack
(2.4.1) if it is opening bracket, then discard it, Go to step (1)
(2.4.2) Pop is used three times
The first popped element is assigned to op2
The second popped element is assigned to op
The third popped element is assigned to op1
Evaluate op1 op op2
Convert the result into character and
push into the stack
Go to step (2.4)
New line character (2.5) Pop from stack and print the answer
STOP
结果: 对完全括号化的中缀表达式的求值将以以下方式打印在显示器上
输入字符串 (((2 * 5) - (1 * 2)) / (9 - 7))
| 输入符号 | 堆栈(从底部到顶部) | 操作 |
|---|---|---|
| ( | ( | |
| ( | ( ( | |
| ( | ( ( ( | |
| 2 | ( ( ( 2 | |
| * | ( ( ( 2 * | |
| 5 | ( ( ( 2 * 5 | |
| ) | ( ( 10 | 2 * 5 = 10 & 压入 |
| - | ( ( 10 - | |
| ( | ( ( 10 - ( | |
| 1 | ( ( 10 - ( 1 | |
| * | ( ( 10 - ( 1 * | |
| 2 | ( ( 10 - ( 1 * 2 | |
| ) | ( ( 10 - 2 | 1 * 2 = 2 & 压入 |
| ) | ( 8 | 10 - 2 = 8 & 压入 |
| / | ( 8 / | |
| ( | ( 8 / ( | |
| 9 | ( 8 / ( 9 | |
| - | ( 8 / ( 9 - | |
| 9 | ( 8 / ( 9 - 7 | |
| ) | ( 8 / 2 | 9 - 7 = 2 & 压入 |
| ) | 4 | 8 / 2 = 4 & 压入 |
| 新行 | 空 | 弹出 & 打印 |
C 程序
int main (int argc, char
struct ch *charactop;
struct integer *integertop;
char rd, op;
int i = 0, op1, op2;
charactop = cclearstack();
integertop = iclearstack();
while(1)
{
rd = argv[1][i++];
switch(rd)
{
case '+':
case '-':
case '/':
case '*':
case '(': charactop = cpush(charactop, rd);
break;
case ')': integertop = ipop (integertop, &op2);
integertop = ipop (integertop, &op1);
charactop = cpop (charactop, &op);
while(op != '(')
{
integertop = ipush (integertop, eval(op, op1, op2));
charactop = cpop (charactop, &op);
if (op != '(')
{
integertop = ipop(integertop, &op2);
integertop = ipop(integertop, &op1);
}
}
break;
case '\0': while (! cemptystack(charactop))
{
charactop = cpop(charactop, &op);
integertop = ipop(integertop, &op2);
integertop = ipop(integertop, &op1);
integertop = ipush(integertop, eval(op, op1, op2));
}
integertop = ipop(integertop, &op1);
printf("\n The final solution is: %d\n", op1);
return 0;
default: integertop = ipush(integertop, rd - '0');
}
}
}
int eval(char op, int op1, int op2)
{
switch (op)
{
case '+': return op1 + op2;
case '-': return op1 - op2;
case '/': return op1 / op2;
case '*': return op1 * op2;
}
}
程序的输出
在命令行输入的输入: (((2 * 5) - (1 * 2)) / (9 - 7)) [3]
输入 (2 * 5 - 1 * 2) / (11 - 9)
输出 4
分析: 有五种类型的输入字符,它们是
* Opening brackets
* Numbers
* Operators
* Closing brackets
* New line character (\n)
如果将操作符读作输入字符,我们不知道该怎么办。通过实现操作符的优先级规则,我们对这个问题有一个解决方案。
优先级规则 我们应该在读入操作符时执行比较优先级检查,然后压入它。如果堆栈的 顶部 包含优先级高于或等于输入操作符优先级的操作符,那么我们就 弹出 它并打印它。我们不断执行优先级检查,直到堆栈的 顶部 或者包含优先级较低的运算符,或者不包含运算符。
此问题的数据结构要求: 字符堆栈和整数堆栈
算法
1. Read an input character
2. Actions that will be performed at the end of each input
Opening brackets (2.1) Push it into stack and then Go to step (1)
Digit (2.2) Push into stack, Go to step (1)
Operator (2.3) Do the comparative priority check
(2.3.1) if the character stack's top contains an operator with equal
or higher priority, then pop it into op
Pop a number from integer stack into op2
Pop another number from integer stack into op1
Calculate op1 op op2 and push the result into the integer
stack
Closing brackets (2.4) Pop from the character stack
(2.4.1) if it is an opening bracket, then discard it and Go to
step (1)
(2.4.2) To op, assign the popped element
Pop a number from integer stack and assign it op2
Pop another number from integer stack and assign it
to op1
Calculate op1 op op2 and push the result into the integer
stack
Convert into character and push into stack
Go to the step (2.4)
New line character (2.5) Print the result after popping from the stack
STOP
结果: 对非完全括号化的中缀表达式的求值将以以下方式打印
输入字符串 (2 * 5 - 1 * 2) / (11 - 9)
| 输入符号 | 字符堆栈(从底部到顶部) | 整数堆栈(从底部到顶部) | 执行的操作 |
|---|---|---|---|
| ( | ( | ||
| 2 | ( | 2 | |
| * | ( * | 压入 因为 * 优先级更高 | |
| 5 | ( * | 2 5 | |
| - | ( * | 由于 - 优先级较低,我们执行 2 * 5 = 10 | |
| ( - | 10 | 我们压入 10,然后压入 - | |
| 1 | ( - | 10 1 | |
| * | ( - * | 10 1 | 压入 * 因为它优先级更高 |
| 2 | ( - * | 10 1 2 | |
| ) | ( - | 10 2 | 执行 1 * 2 = 2 并压入它 |
| ( | 8 | 弹出 - 和 10 - 2 = 8 并压入,弹出 ( | |
| / | / | 8 | |
| ( | / ( | 8 | |
| 11 | / ( | 8 11 | |
| - | / ( - | 8 11 | |
| 9 | / ( - | 8 11 9 | |
| ) | / | 8 2 | 执行 11 - 9 = 2 并压入它 |
| 新行 | 4 | 执行 8 / 2 = 4 并压入它 | |
| 4 | 打印输出,即 4 |
C 程序
int main (int argc, char *argv[])
{
struct ch *charactop;
struct integer *integertop;
char rd, op;
int i = 0, op1, op2;
charactop = cclearstack();
integertop = iclearstack();
while(1)
{
rd = argv[1][i++];
switch(rd)
{
case '+':
case '-':
case '/':
case '*': while ((charactop->data != '(') && (!cemptystack(charactop)))
{
if(priority(rd) > (priority(charactop->data))
break;
else
{
charactop = cpop(charactop, &op);
integertop = ipop(integertop, &op2);
integertop = ipop(integertop, &op1);
integertop = ipush(integertop, eval(op, op1, op2);
}
}
charactop = cpush(charactop, rd);
break;
case '(': charactop = cpush(charactop, rd);
break;
case ')': integertop = ipop (integertop, &op2);
integertop = ipop (integertop, &op1);
charactop = cpop (charactop, &op);
while(op != '(')
{
integertop = ipush (integertop, eval(op, op1, op2);
charactop = cpop (charactop, &op);
if (op != '(')
{
integertop = ipop(integertop, &op2);
integertop = ipop(integertop, &op1);
}
}
break;
case '\0': while (!= cemptystack(charactop))
{
charactop = cpop(charactop, &op);
integertop = ipop(integertop, &op2);
integertop = ipop(integertop, &op1);
integertop = ipush(integertop, eval(op, op1, op2);
}
integertop = ipop(integertop, &op1);
printf("\n The final solution is: %d", op1);
return 0;
default: integertop = ipush(integertop, rd - '0');
}
}
}
int eval(char op, int op1, int op2)
{
switch (op)
{
case '+': return op1 + op2;
case '-': return op1 - op2;
case '/': return op1 / op2;
case '*': return op1 * op2;
}
}
int priority (char op)
{
switch(op)
{
case '^':
case '$': return 3;
case '*':
case '/': return 2;
case '+':
case '-': return 1;
}
}
程序的输出
在命令行输入的输入 (2 * 5 - 1 * 2) / (11 - 9)
输出: 4 [3]
输入: x + 6 * ( y + z ) ^ 3
输出:' 4
分析: 有三种类型的输入字符
* Numbers
* Operators
* New line character (\n)
数据结构要求: 字符堆栈和整数堆栈
算法
1. Read one character input at a time and keep pushing it into the character stack until the new
line character is reached
2. Perform pop from the character stack. If the stack is empty, go to step (3)
Number (2.1) Push in to the integer stack and then go to step (1)
Operator (2.2) Assign the operator to op
Pop a number from integer stack and assign it to op1
Pop another number from integer stack
and assign it to op2
Calculate op1 op op2 and push the output into the integer
stack. Go to step (2)
3. Pop the result from the integer stack and display the result
结果: 前缀表达式的求值将以以下方式打印
输入字符串 / - * 2 5 * 1 2 - 11 9
| 输入符号 | 字符堆栈(从底部到顶部) | 整数堆栈(从底部到顶部) | 执行的操作 |
|---|---|---|---|
| / | / | ||
| - | / | ||
| * | / - * | ||
| 2 | / - * 2 | ||
| 5 | / - * 2 5 | ||
| * | / - * 2 5 * | ||
| 1 | / - * 2 5 * 1 | ||
| 2 | / - * 2 5 * 1 2 | ||
| - | / - * 2 5 * 1 2 - | ||
| 11 | / - * 2 5 * 1 2 - 11 | ||
| 9 | / - * 2 5 * 1 2 - 11 9 | ||
| \n | / - * 2 5 * 1 2 - 11 | 9 | |
| / - * 2 5 * 1 2 - | 9 11 | ||
| / - * 2 5 * 1 2 | 2 | 11 - 9 = 2 | |
| / - * 2 5 * 1 | 2 2 | ||
| / - * 2 5 * | 2 2 1 | ||
| / - * 2 5 | 2 2 | 1 * 2 = 2 | |
| / - * 2 | 2 2 5 | ||
| / - * | 2 2 5 2 | ||
| / - | 2 2 10 | 5 * 2 = 10 | |
| / | 2 8 | 10 - 2 = 8 | |
| 堆栈为空 | 4 | 8 / 2 = 4 | |
| 堆栈为空 | 打印 4 |
C 程序
int main (int argc, char *argv[])
{
struct ch *charactop = NULL;
struct integer *integertop = NULL;
char rd, op;
int i = 0, op1, op2;
charactop = cclearstack();
integertop = iclearstack();
rd = argv[1][i];
while(rd != '\0')
{
charactop = cpush(charactop, rd);
rd = argv[1][i++];
}
while(!emptystack(charactop))
{
charactop = cpop(charactop, rd);
switch(rd)
{
case '+':
case '-':
case '/':
case '*':
op = rd;
integertop = ipop(integertop, &op2);
integertop = ipop(integertop, &op1);
integertop = ipush(integertop, eval(op, op1, op2));
break;
default: integertop = ipush(integertop, rd - '0');
}
}
}
int eval(char op, int op1, int op2)
{
switch (op)
{
case '+': return op1 + op2;
case '-': return op1 - op2;
case '/': return op1 / op2;
case '*': return op1 * op2;
}
}
int priority (char op)
{
switch(op)
{
case '^':
case '$': return 3;
case '*':
case '/': return 2;
case '+':
case '-': return 1;
}
}
程序的输出
在命令行输入的输入: / - * 2 5 * 1 2 - 11 9
输出: 4 [3]
输入 (((8 + 1) - (7 - 4)) / (11 - 9))
输出 8 1 + 7 4 - - 11 9 - /
分析: 有五种类型的输入字符,它们是
* Opening brackets
* Numbers
* Operators
* Closing brackets
* New line character (\n)
要求: 字符堆栈
算法
1. Read an character input
2. Actions to be performed at end of each input
Opening brackets (2.1) Push into stack and then Go to step (1)
Number (2.2) Print and then Go to step (1)
Operator (2.3) Push into stack and then Go to step (1)
Closing brackets (2.4) Pop it from the stack
(2.4.1) If it is an operator, print it, Go to step (1)
(2.4.2) If the popped element is an opening bracket,
discard it and go to step (1)
New line character (2.5) STOP
因此,将中缀表达式转换为后缀表达式后的最终输出如下所示
| 输入 | 操作 | 堆栈(操作后) | 显示器上的输出 |
|---|---|---|---|
| ( | (2.1) 将操作数压入堆栈 | ( | |
| ( | (2.1) 将操作数压入堆栈 | ( ( | |
| ( | (2.1) 将操作数压入堆栈 | ( ( ( | |
| 8 | (2.2) 打印它 | 8 | |
| + | (2.3) 将操作符压入堆栈 | ( ( ( + | 8 |
| 1 | (2.2) 打印它 | 8 1 | |
| ) | (2.4) 从堆栈中弹出: 由于弹出的元素是 +,所以打印它 | ( ( ( | 8 1 + |
| (2.4) 从堆栈中弹出: 由于弹出的元素是 (,所以我们忽略它并读取下一个字符 | ( ( | 8 1 + | |
| - | (2.3) 将操作符压入堆栈 | ( ( - | |
| ( | (2.1) 将操作数压入堆栈 | ( ( - ( | |
| 7 | (2.2) 打印它 | 8 1 + 7 | |
| - | (2.3) 将操作符压入堆栈 | ( ( - ( - | |
| 4 | (2.2) 打印它 | 8 1 + 7 4 | |
| ) | (2.4) 从堆栈中弹出: 由于弹出的元素是 -,所以打印它 | ( ( - ( | 8 1 + 7 4 - |
| (2.4) 从堆栈中弹出: 由于弹出的元素是 (,所以我们忽略它并读取下一个字符 | ( ( - | ||
| ) | (2.4) 从堆栈中弹出: 由于弹出的元素是 -,所以打印它 | ( ( | 8 1 + 7 4 - - |
| (2.4) 从堆栈中弹出: 由于弹出的元素是 (,所以我们忽略它并读取下一个字符 | ( | ||
| / | (2.3) 将操作数压入堆栈 | ( / | |
| ( | (2.1) 压入堆栈 | ( / ( | |
| 11 | (2.2) 打印它 | 8 1 + 7 4 - - 11 | |
| - | (2.3) 将操作数压入堆栈 | ( / ( - | |
| 9 | (2.2) 打印它 | 8 1 + 7 4 - - 11 9 | |
| ) | (2.4) 从堆栈中弹出: 由于弹出的元素是 -,所以打印它 | ( / ( | 8 1 + 7 4 - - 11 9 - |
| (2.4) 从堆栈中弹出: 由于弹出的元素是 (,所以我们忽略它并读取下一个字符 | ( / | ||
| ) | (2.4) 从堆栈中弹出: 由于弹出的元素是 /,所以打印它 | ( | 8 1 + 7 4 - - 11 9 - / |
| (2.4) 从堆栈中弹出: 由于弹出的元素是 (,所以我们忽略它并读取下一个字符 | 堆栈为空 | ||
| 换行符 | (2.5) 停止 |
这是一个关于堆栈的非常好的应用。假设一列货运列车有 n 节车厢,每节车厢都将在不同的车站卸货。它们从 1 到 n 编号,货运列车按照从 n 到 1 的顺序访问这些车站。显然,火车车厢按其目的地进行标记。为了方便从列车中卸下车厢,我们必须将它们按其编号(即从 1 到 n)的升序排列。当车厢按此顺序排列时,它们可以在每个车站被分离。我们在一个有 输入轨道、输出轨道 和 k 个位于输入和输出轨道之间的中间轨道(即 中间轨道)的调车场重新排列车厢。
为了重新排列车厢,我们从前到后检查输入轨道上的车厢。如果正在检查的车厢是输出排列中的下一个车厢,那么我们将它直接移动到 输出轨道。如果不是,我们将它移动到 中间轨道 并将它留在那里,直到将它放到 输出轨道 上。中间轨道以 LIFO 的方式运行,因为车厢从顶部进入和离开这些轨道。当重新排列车厢时,只允许以下移动
- 车厢可以从输入轨道的最前端(即右端)移动到中间轨道的顶部,也可以移动到输出轨道的左端。
- 车厢可以从中间轨道的顶部移动到输出轨道的左端。
图中显示了一个 k = 3 的调车场,中间轨道为 H1、H2 和 H3,n = 9。货运列车的 n 节车厢从输入轨道开始,最终以从右到左的顺序 1 到 n 排列在输出轨道上。车厢最初以从后到前的顺序为 5、8、1、7、4、2、9、6、3。后续的车厢将以所需的顺序进行重新排列。

- 考虑图中的输入排列,我们注意到汽车 3 在最前面,所以它还不能输出,因为它需要先于汽车 1 和 2 输出。所以,汽车 3 被分离并移动到保持轨道 H1 上。
- 下一辆汽车 6 无法输出,它被移动到保持轨道 H2 上。因为我们必须先输出汽车 3 才能输出汽车 6,如果我们将汽车 6 移动到保持轨道 H1 上,这是不可能的。
- 现在很明显,我们将汽车 9 移动到 H3 上。
对保持轨道上汽车进行重新排列的要求是,汽车应按从上到下的升序排列。
- 因此,现在将汽车 2 移动到保持轨道 H1 上,以满足前面的语句。如果我们将汽车 2 移动到 H2 或 H3 上,那么我们将没有地方移动汽车 4、5、7 或 8。当新的汽车 λ 被移动到保持轨道上时,对未来汽车放置的限制最小,该保持轨道的顶部有一个标签为 Ψ 的汽车,其中 λ < Ψ。我们可以称其为分配规则,用于决定特定汽车是否属于特定保持轨道。
- 当考虑汽车 4 时,有三个地方可以移动汽车:H1、H2 和 H3。这些轨道顶部分别是 2、6 和 9。所以使用上述分配规则,我们将汽车 4 移动到 H2 上。
- 汽车 7 被移动到 H3 上。
- 下一辆汽车 1 的标签最小,所以它被移动到输出轨道上。
- 现在是时候输出汽车 2 和 3 了,它们来自 H1(简而言之,来自 H1 的所有汽车都被附加到输出轨道上的汽车 1 上)。
汽车 4 被移动到输出轨道上。此时,没有其他汽车可以被移动到输出轨道上。
- 下一辆汽车,汽车 8,被移动到保持轨道 H1 上。
- 汽车 5 从输入轨道输出。汽车 6 从 H2 移动到输出轨道,汽车 7 从 H3 移动到输出轨道,汽车 8 从 H1 移动到输出轨道,汽车 9 从 H3 移动到输出轨道。
排序意味着以特定顺序排列一组元素。无论是升序还是降序,按基数还是字母顺序,或其变体。产生的排序可能性将仅受源元素类型的限制。
快速排序是一种分治类型的算法。在这种方法中,为了对一组数字进行排序,我们将它缩减为两个更小的集合,然后对这两个更小的集合进行排序。
这可以用以下示例来解释
假设A是以下数字的列表
在缩减步骤中,我们找到其中一个数字的最终位置。在本例中,假设我们必须找到 48 的最终位置,它是列表中的第一个数字。
为了实现这一点,我们采用以下方法。从最后一个数字开始,从右到左移动。将每个数字与 48 进行比较。如果数字小于 48,我们停止在该数字处并将它与 48 进行交换。
在我们的例子中,数字是 24。因此,我们将 24 和 48 进行交换。
48 右侧的数字 96 和 72 大于 48。现在从 24 开始,以相反的方向扫描数字,即从左到右。将每个数字与 48 进行比较,直到找到一个大于 48 的数字。
在本例中,它是 60。因此,我们将 48 和 60 进行交换。
注意,48 左侧的数字 12、24 和 36 都小于 48。现在,从 60 开始,从右到左方向扫描数字。一旦找到较小的数字,就将其与 48 进行交换。
在本例中,它是 44。将其与 48 进行交换。最终结果是
现在,从 44 开始,从左到右扫描列表,直到找到一个大于 48 的数字。
这样一个数字是 84。将其与 48 进行交换。最终结果是
现在,从 84 开始,从右到左遍历列表,直到到达小于 48 的数字。在到达 48 之前,我们没有找到这样的数字。这意味着列表中的所有数字都已扫描并与 48 进行比较。此外,我们注意到所有小于 48 的数字都在它左侧,所有大于 48 的数字都在它右侧。
最终分区如下所示
因此,48 已被放置到其正确的位置,现在我们的任务减少到对两个分区进行排序。这个创建分区的步骤可以对每个包含 2 个或多个元素的分区重复进行。因为我们一次只能处理一个分区,所以我们应该能够跟踪其他分区,以便将来进行处理。
这是通过使用两个名为 LOWERBOUND 和 UPPERBOUND 的堆栈来临时存储这些分区来完成的。分区的第一个和最后一个元素的地址分别被推入 LOWERBOUND 和 UPPERBOUND 堆栈。现在,只有在从堆栈中弹出其边界值后,才会将上述缩减步骤应用于分区。
我们可以从以下示例中理解这一点
以包含 12 个元素的上述列表 A 为例。该算法首先将 A 的边界值,即 1 和 12,分别推入 LOWERBOUND 和 UPPERBOUND 堆栈。因此,堆栈如下所示
LOWERBOUND: 1 UPPERBOUND: 12
为了执行缩减步骤,堆栈顶部的值将从堆栈中弹出。因此,两个堆栈都变为空。
LOWERBOUND: {empty} UPPERBOUND: {empty}
现在,缩减步骤导致 48 被固定到第 5 个位置,并创建了两个分区,一个是从位置 1 到 4,另一个是从位置 6 到 12。因此,值 1 和 6 被推入 LOWERBOUND 堆栈,4 和 12 被推入 UPPERBOUND 堆栈。
LOWERBOUND: 1, 6 UPPERBOUND: 4, 12
为了再次应用缩减步骤,堆栈顶部的值将被弹出。因此,值 6 和 12 被弹出。因此,堆栈如下所示
LOWERBOUND: 1 UPPERBOUND: 4
现在将缩减步骤应用于第二个分区,即从第 6 个到第 12 个元素。
缩减步骤之后,98 被固定在第 11 个位置。因此,第二个分区只有一个元素。因此,我们将第一个分区的上界和下界值推入堆栈。因此,堆栈如下所示
LOWERBOUND: 1, 6 UPPERBOUND: 4, 10
处理以以下方式进行,并在堆栈不包含要处理的任何分区的上界和下界值,并且列表被排序后结束。
在股票跨度问题中,我们将借助堆栈解决一个金融问题。
假设对于一只股票,我们有一系列n天的每日价格报价,股票价格在某一天的跨度定义为股票价格在当前天小于或等于其价格的连续天数的最大值。
输入:一个包含n个元素的数组P
输出:一个包含n个元素的数组S,使得 S[i] 是最大的整数 k,使得 k <= i + 1 且 P[j] <= P[i] 对于 j = i - k + 1,.....,i
算法
1. Initialize an array P which contains the daily prices of the stocks
2. Initialize an array S which will store the span of the stock
3. for i = 0 to i = n - 1
3.1 Initialize k to zero
3.2 Done with a false condition
3.3 repeat
3.3.1 if (P[i - k] <= P[i]) then
Increment k by 1
3.3.2 else
Done with true condition
3.4 Till (k > i) or done with processing
Assign value of k to S[i] to get the span of the stock
4. Return array S
现在,分析该算法的运行时间,我们观察到
- 我们在开始时初始化了数组 S,并在结束时返回它。这是一个常数时间操作,因此需要O(n) 时间。
- repeat 循环嵌套在for 循环中。for 循环,其计数器为i,执行了 n 次。不在 repeat 循环中,而在 for 循环中的语句执行了n次。因此,这些语句以及 i 的递增和条件测试需要O(n) 时间。
- 在外部 for 循环的 i 重复中,内部repeat 循环的主体最多执行 i + 1 次。在最坏情况下,元素 S[i] 大于所有之前的元素。因此,测试 if 条件、该条件后的语句以及测试 until 条件将在外部 for 循环的迭代 i 中执行 i + 1 次。因此,内部循环的总时间为O(n(n + 1)/2),即O()
所有这些步骤的运行时间是通过将所有这三个步骤所花费的时间相加来计算的。前两项是O(),而最后一项是O()。因此,该算法的总运行时间为O()。
为了更有效地计算跨度,我们发现,如果我们知道在i之前最近的日期,使得该日期的股票价格高于当前日期的股票价格,则可以很容易地计算出特定日期的跨度。如果存在这样的日期,我们可以用 h(i) 来表示它,并将 h(i) 初始化为 -1。
因此,特定日期的跨度由以下公式给出:s = i - h(i)。
为了实现此逻辑,我们使用堆栈作为抽象数据类型来存储日期 i、h(i)、h(h(i)) 等等。当我们从第 i-1 天到第 i 天时,我们将弹出会弹出股票价格小于或等于 p(i) 的日期,然后将日期 i 的值压回堆栈。
这里,我们假设堆栈是通过占用O(1)(即常数时间)的操作来实现的。该算法如下:
输入:一个包含n个元素的数组 P 和一个空的堆栈 N
输出:一个包含n个元素的数组S,使得 P[i] 是最大的整数 k,满足 k <= i + 1 且对于 j = i - k + 1,.....,i,P[y] <= P[i]。
算法
1. Initialize an array P which contains the daily prices of the stocks
2. Initialize an array S which will store the span of the stock
3. for i = 0 to i = n - 1
3.1 Initialize k to zero
3.2 Done with a false condition
3.3 while not (Stack N is empty or done with processing)
3.3.1 if ( P[i] >= P[N.top())] then
Pop a value from stack N
3.3.2 else
Done with true condition
3.4 if Stack N is empty
3.4.1 Initialize h to -1
3.5 else
3.5.1 Initialize stack top to h
3.5.2 Put the value of h - i in S[i]
3.5.3 Push the value of i in N
4. Return array S
现在,分析该算法的运行时间,我们观察到
- 我们在开始时初始化了数组 S,并在结束时返回它。这是一个常数时间操作,因此需要O(n) 时间。
- while 循环嵌套在for 循环中。for 循环的计数器是i,执行 n 次。不在重复循环中,但在 for 循环中的语句执行n 次。因此,这些语句以及 i 的递增和条件测试需要O(n) 时间。
- 现在,观察for 循环的i 次重复期间的内部 while 循环。语句done with a true condition 最多执行一次,因为它会导致退出循环。假设 t(i) 是语句Pop a value from stack N 执行的次数。因此,很明显,while not (Stack N is empty or done with processing) 最多被测试 t(i) + 1 次。
- 将 while 循环中所有操作的运行时间相加,我们得到
- 一旦从堆栈 N 中弹出元素,就永远不会再压回堆栈。因此,
因此,while 循环中所有语句的运行时间为O()
通过将所有这些步骤所花费的时间相加,可以计算出算法中所有步骤的运行时间。每个步骤的运行时间为O()。因此,该算法的运行时间复杂度为O()。
相关链接
[edit | edit source]队列
[edit | edit source]队列是一种基本的数据结构,在整个编程中使用。您可以将其视为杂货店里的队伍。排在队伍最前面的人是最先得到服务的人,就像队列一样。
队列也称为 FIFO(先进先出),以展示其访问数据的方式。
Queue<item-type> 操作
enqueue(new-item:item-type)- 将一个项目添加到队列的末尾。
front():item-type- 返回队列最前面的项目。
dequeue()- 从队列中移除最前面的项目。
is-empty():Boolean- 如果不再有项目可以出队,并且没有最前面的项目,则为真。
is-full():Boolean- 如果不再有项目可以入队,则为真。
get-size():Integer- 返回队列中的元素数量。
除了 get-size() 之外的所有操作都可以在 时间内完成。get-size() 最坏情况下运行在
链表实现
[edit | edit source]基本链表实现使用单链表,并使用尾指针跟踪队列的尾部。
type Queue<item_type>
data list:Singly Linked List<item_type>
data tail:List Iterator<item_type>
constructor()
list := new Singly-Linked-List()
tail := list.get-begin() # null
end constructor
当您想要入队某些内容时,只需将其添加到尾指针所指向的项目后面即可。因此,与添加的项目相比,之前的尾部被视为下一个,并且尾指针指向新项目。如果列表为空,则此方法不适用,因为尾部迭代器不引用任何内容。
method enqueue(new_item:item_type)
if is-empty()
list.prepend(new_item)
tail := list.get-begin()
else
list.insert_after(new_item, tail)
tail.move-next()
end if
end method
队列中的最前面的项目只是链表的头部指针所引用的项目。
method front():item_type
return list.get-begin().get-value()
end method
当您想要从列表中出队某些内容时,只需将头部指针指向头部项目的 previous 即可。旧的头部项目是您从列表中移除的项目。如果列表现在为空,我们必须修复尾部迭代器。
method dequeue()
list.remove-first()
if is-empty()
tail := list.get-begin()
end if
end method
检查是否为空很容易。只需检查列表是否为空。
method is-empty():Boolean
return list.is-empty()
end method
检查是否已满很简单。链表被认为是无限大小的。
method is-full():Boolean
return False
end method
检查大小也会传递到列表中。
method get-size():Integer
return list.get-size()
end method
end type
性能分析
[edit | edit source]在链表中,访问第一个元素是一个 操作,因为列表包含一个指向它的指针。因此,入队、最前面和出队都是快速 操作。
这里所做的空/满检查也是。
getSize() 的性能取决于链表实现中相应操作的性能。它可能是 ,或 ,取决于所做的时间/空间权衡。大多数情况下,队列的用户不使用 getSize() 操作,因此可以通过不优化它来节省一些空间。
循环数组实现
[edit | edit source]性能分析
[edit | edit source]优先队列实现
[edit | edit source]
相关链接
[edit | edit source]双端队列
[edit | edit source]双端队列是一种同构元素列表,其中在两端都执行插入和删除操作。
由于这种特性,它被称为双端队列,即双端队列。
双端队列有两种类型
- 输入受限队列:它只允许在一端插入
- 输出受限队列:它只允许在一端删除
参考文献
[edit | edit source]树
[edit | edit source]树是一个非空集合,其中一个元素被指定为树的根,而剩余元素被划分成非空集合,每个集合都是根的子树。
树节点具有许多有用的属性。节点的深度是从根到该节点的路径的长度(或边的数量)。节点的高度是从该节点到其叶子的最长路径。树的高度是根的高度。叶节点没有子节点——它唯一的路径是向上到其父节点。
请参阅树的公理化发展及其后果以获取更多信息。
树的类型
二叉树:每个节点有零个、一个或两个子节点。此断言使许多树操作变得简单高效。
二叉搜索树:二叉树,其中任何左子节点的值都小于其父节点,任何右子节点的值都大于或等于其父节点的值。
遍历
[edit | edit source]许多问题需要我们以一种系统的方式访问树的节点:例如计算存在多少个节点或找到最大元素的任务。对于二叉树,有三种不同的方法:前序、后序和中序,它们都执行相同的三个操作:递归遍历左子树和右子树并访问当前节点。不同之处在于算法访问当前节点的时间
前序:当前节点、左子树、右子树(DLR)
后序:左子树、右子树、当前节点(LRD)
中序:左子树、当前节点、右子树(LDR)
层序:从根节点开始,逐层从左到右。
- 访问意味着执行一些涉及树中当前节点的操作,比如增加计数器或检查当前节点的值是否大于任何其他记录的值。
树遍历的示例实现
[edit | edit source]preorder(node) visit(node) if node.left ≠ null then preorder(node.left) if node.right ≠ null then preorder(node.right)
inorder(node) if node.left ≠ null then inorder(node.left) visit(node) if node.right ≠ null then inorder(node.right)
postorder(node) if node.left ≠ null then postorder(node.left) if node.right ≠ null then postorder(node.right) visit(node)
levelorder(root) queue<node> q q.push(root) while not q.empty do node = q.pop visit(node) if node.left ≠ null then q.push(node.left) if node.right ≠ null then q.push(node.right)
对于对堆栈要求较低的算法,请参阅线程树。
树遍历的示例
[edit | edit source]preorder: 50,30, 20, 40, 90, 100 inorder: 20,30,40,50, 90, 100 postorder: 20,40,30,100,90,50
平衡
[edit | edit source]当已经排序的条目存储在树中时,所有新记录都将走相同的路线,树看起来更像一个列表(这样的树称为退化树)。因此,树需要平衡例程,确保所有分支下都有相同数量的记录。这将使树中的搜索保持最佳速度。具体来说,如果具有n个节点的树是退化树,则通过树的最长路径将是 n 个节点;如果它是平衡树,则最长路径将是log n个节点。
Algorithms/左旋: 本文展示了如何在 树堆 中应用平衡操作来建立优先堆不变式。树堆是一种数据结构,它具有堆的队列性能和树的关键查找性能。平衡操作可以在保持另一种排序(即二叉树排序)的同时改变树的结构。二叉树排序的顺序是从左到右,左节点的键小于右节点的键,而优先级排序是从上到下,较高级别的节点的优先级高于较低级别的节点。或者,优先级可以被看作另一个排序键,只是查找特定键的过程更加复杂。
平衡操作可以在不影响左右顺序的情况下将节点上下移动。
AVL 树: 按照以下规范进行平衡的二叉搜索树:任何节点的两个子树的高度差最多为 1。
红黑树: 一种平衡的二叉搜索树,使用基于分配给节点的颜色以及附近节点的颜色进行平衡算法。
AA 树: 一种平衡树,实际上是红黑树的一种更严格的变体。
典型的二叉搜索树如下所示
节点 存储在树中的任何项。根节点 树中最顶端的项。(上图中的树为 50)子节点 当前节点下方的节点。(上图中的树为 30 的子节点为 20 和 40)父节点 当前节点正上方的节点。(上图中的树为 100 的父节点为 90)叶节点 没有子节点的节点。(上图中的树为 20 是叶节点)
要在二叉树中搜索项目,请执行以下操作
- 从根节点开始
- 如果您要搜索的项目小于根节点,则移至根节点的左子节点;如果您要搜索的项目大于根节点,则移至根节点的右子节点;如果它等于根节点,则表示您已经找到了要查找的项目。
- 现在检查您要搜索的项目是否等于、小于或大于您当前所在的节点。同样地,如果要搜索的项目小于当前节点,则移至左子节点;如果要搜索的项目大于当前节点,则移至右子节点。
- 重复此过程,直到找到要搜索的项目,或直到节点在正确的分支上没有子节点,在这种情况下,树不包含您要查找的项目。
例如,要查找节点 40...
- 根节点是 50,它大于 40,因此您移至 50 的左子节点。
- 50 的左子节点是 30,它小于 40,因此您接下来移至 30 的右子节点。
- 30 的右子节点是 40,因此您已经找到了要搜索的项目 :)
.........
- 要添加项目,您首先必须搜索树以找到应放置它的位置。您可以按照上面的步骤进行操作。
- 当您到达在正确分支上没有子节点的节点时,请在该位置添加新节点。
例如,要添加节点 25...
- 根节点是 50,它大于 25,因此您移至 50 的左子节点。
- 50 的左子节点是 30,它大于 25,因此您移至 30 的左子节点。
- 30 的左子节点是 20,它小于 25,因此您移至 20 的右子节点。
- 20 的右子节点不存在,因此您在该位置添加 25 :)
假设您已经使用上面描述的搜索技术找到了要删除的节点。
例如,要删除 40...
- 只需删除节点!
- 将要删除的节点的子节点直接连接到要删除的节点的父节点。
例如,要删除 90...
- 删除 90,然后将 100 设为 50 的子节点。
一种非标准方法是将节点旋转到选定的子树中,并尝试从该子树中递归删除键,直到出现情况 1 或情况 2 为止。这可能会使树失去平衡,因此随机选择向右或向左旋转可能会有所帮助。
标准方法是选择左子树或右子树,例如右子树,然后通过从右子树开始一直向左移动,直到下一个左节点为空,从而获取右子树的最左侧后代。然后删除右子树的这个最左侧后代,用它的右子树(它有一个空的左子树)来替换它。然后使用这个以前右子树的最左侧后代的内容来替换要删除的节点的键和值,以便它的值现在位于要删除的节点(右子树的父节点)中。这仍然可以保持所有节点的键排序。示例 Java 代码在下面的树堆示例代码中。
以下示例使用标准算法,即后继节点是待删除节点的右子树中的最左侧节点。
例如,要删除 30
- 要删除的节点的右节点是 40。
- (从现在开始,我们一直移至左节点,直到没有另一个节点……)40 的第一个左节点是 35。
- 35 没有左节点,因此 35 是后继节点!
- 35 替换了原始右节点的 30,并且包含 35 的节点被删除,用具有根节点 37 的右子树来替换它。
- 将待删除节点右侧的子节点直接移至待删除节点的位置。
- 由于新节点没有左子节点,因此您可以将待删除节点的左子树的根节点连接为它的左子节点。
例如,要删除 30
- 用后继节点的内容(40)替换要删除的内容(30)。
- 删除后继节点(内容为 40),用它的右子树(头节点内容为 45)来替换它。
这最好用一个例子来解释。
要删除 30...
- 将要删除的内容(30)替换为后继节点的内容(35)。
- 将后继节点(35)替换为它的右子树(37)。因为后继节点是最左边的节点,所以没有左子树。
private Treap1<K, V>.TreapNode deleteNode(K k, Treap1<K, V>.TreapNode node, Deleted del) {
if (node == null) {
return null;
} else if (k.compareTo(node.k) < 0) {
node.left = deleteNode(k, node.left, del);
} else if (k.compareTo(node.k) > 0) {
node.right = deleteNode(k, node.right, del);
// k.compareTo(node.k) == 0
} else if ( node.left == null ) {
del.success = true;
return node.right;
} else if ( node.right == null) {
del.success = true;
return node.left;
} else if (node.left !=null && node.right != null){
/*
// non-standard method,
// left rotate and all delete on left subtree
TreapNode tmp = node.right;
node.right = node.right.left;
tmp.left = node;
node = tmp;
node.left = deleteNode(k , node.left, del);
*/
// more standard method ? doesn't disturb tree structure as much
// find leftmost descendant of the right child node and replace contents
TreapNode n2 = node.right;
TreapNode previous2 = null;
while (n2.left != null) {
previous2 = n2;
n2 = n2.left;
}
if (previous2 != null) {
previous2.left = n2.right;
//n2 has no parent link, orphaned
} else {
node.right = n2.right;
//n2 has no parent link, orphaned
}
node.k = n2.k;
node.val = n2.val;
del.success = true;
// once n2 out of scope, the orphaned node at n2 will be garbage collected,
}
return node;
}
红黑树是一种自平衡树结构,它为每个节点分配一个颜色。红黑树的结构必须遵守一套规则,这些规则规定了不同颜色节点的排列方式。当树以某种方式修改时,会应用这些规则,导致在插入新节点或删除旧节点时,某些节点旋转和重新着色。这保持了红黑树的平衡,保证了 O(log n) 的搜索复杂度。
红黑树必须遵守的规则如下:
- 每个节点必须是红色或黑色。
- 根节点始终是黑色的。
- 树中的所有叶子节点都是黑色的(叶子节点不包含数据,在大多数编程语言中可以建模为 null 或 nil 引用)。
- 每个红色节点必须有两个黑色子节点。
- 从给定节点到其任何后代叶节点的每条路径必须包含相同数量的黑色节点。
红黑树可以建模为 2-3-4 树,它是 B 树(见下文)的一个子类。一个黑色节点带有一个红色节点可以看作是链接在一起的 3 节点,一个黑色节点带两个红色子节点可以看作是 4 节点。
4 节点会被 拆分,生成两个节点,并将中间节点变为红色,这会将中间节点的父节点(没有红色子节点)从 2 节点变为 3 节点,并将具有一个红色子节点的父节点变为 4 节点(但这不会发生在始终是左边的红色节点的情况下)。
两个红色节点的内联排列会被 旋转 成一个具有两个红色子节点的父节点,即一个 4 节点,然后会 拆分,如前所述。
A right rotate 'split 4-node' |red
red / \ --> B ---> B
B red/ \red / \
red / \ C A C A
C D / /
D D
Sedgewick 提到的一个优化是,所有右插入的红色节点都会被左旋转成左红色节点,因此只有内联的左红色节点需要在拆分之前进行右旋转。Arne Anderson 提出的 AA 树(见上文),在 1993 年的一篇论文中描述了这种简化的早期阐述,但他建议使用右倾斜的“红色标记”,而不是 Sedgewick 建议的左倾斜,但 AA 树似乎优先于左倾斜的红黑树。如果 Linux CFS 调度程序在将来被描述为“基于 AA 的”,这将是一个相当大的冲击。
总之,红黑树是一种检测对同一侧进行两次插入并使树在情况变得更糟之前进行平衡的方法。两次左侧插入将被旋转,两次右侧插入看起来像是两次左侧插入,因为左旋转会移除右倾斜的红色节点。两次对同一个父节点的平衡插入会导致 4 节点拆分而无需旋转,因此出现了一个问题:红黑树是否可以被 a < P < b 形式的单侧三元组的串行插入所攻击,然后是下一个三元组的 P' < a。
以下为 Python 示例代码
RED = 1
BLACK = 0
class Node:
def __init__(self, k, v):
# all newly inserted node's are RED
self.color = RED
self.k = k
self.v = v
self.left = None
self.right = None
class RBTree:
def __init__(self):
self.root = None
def insert(self, k, v) :
self.root = self._insert(self.root, k,v)
def _insert(self, n , k, v):
if n is None:
return Node(k,v)
if k < n.k :
n.left = self._insert(n.left, k , v)
elif k > n.k :
n.right = self._insert(n.right, k, v)
if n.right.color is RED:
#always on the left red's
#left rotate
tmp = n.right
n.right = tmp.left
tmp.left = n
n = tmp
#color rotation is actually a swap
tmpcolor = n.color
n.color = n.left.color
n.left.color = tmpcolor
if n.left <> None and n.left.left <> None and n.left.left.color == RED and n.left.color == RED:
# right rotate in-line reds
print "right rotate"
tmp = n.left
n.left = tmp.right
tmp.right = n
n = tmp
#color rotation is actually a swap
tmpcolor = n.color
n.color = n.right.color
n.right.color = tmpcolor
if n.left <> None: print n.left.color, n.color, n.right.color
#no need to test, because after right rotation, will need to split 3-node , as right rotation has
#brought red left grandchild to become left red child, and left red child is now red right child
#so there are two red children.
#if n.left <> None and n.right <> None and n.left.color == RED and n.right.color == RED:
print "split"
n.color = RED
n.left.color = BLACK
n.right.color = BLACK
return n
def find(self, k):
return self._find_rb(k, self.root)
def _find_rb(self, k, n):
if n is None:
return None
if k < n.k:
return self._find_rb( k, n.left)
if k > n. k:
return self._find_rb( k, n.right)
return n.v
def inorder(self):
self.inorder_visit(self.root, "O")
def inorder_visit(self, node,label=""):
if node is None: return
self.inorder_visit(node.left, label+"/L")
print label, "val=", node.v
self.inorder_visit(node.right, label+"/R")
def test1(N):
t = RBTree()
for i in xrange(0,N):
t.insert(i,i)
l = []
t.inorder()
for i in xrange(0,N):
x =t.find(i)
if x <> None:
l.append((x, i) )
print "found", len(l)
if __name__ == "__main__":
import random
test1(100000)
test1(1000)
test1(100)
test1(10)
- 二叉树的节点有两个子节点,左子节点及其所有后代节点都小于节点的“值”,右子节点及其所有后代节点都大于节点的“值”,而 B 树是对此的概括。
- 概括在于,节点不是存储一个值,而是存储一个值列表,该列表的长度为 n(n > 2)。n 被选择以优化存储,以便节点的大小对应于一个块的大小。这发生在 SSD 驱动器出现之前的时代,但搜索存储在 SSD RAM 上的二叉节点仍然比搜索 SSD RAM 上的块数据、加载到普通 RAM 和 CPU 缓存以及搜索加载的列表要慢。
- 在列表的开头,第一个元素的左子节点的值小于第一个元素,其所有子节点也是如此。第一个元素的右边是一个子节点,它的值大于第一个元素的值,其所有子节点也是如此,但小于第二个元素的值。可以使用归纳法,对于元素 1 和 2 之间的子节点,2 和 3 之间的子节点,以此类推,直到 n-1 和第 n 个节点都是如此。
- 要插入到一个非满的 B 树节点中,需要对一个排序的列表进行插入操作。
- 在 B+ 树中,插入操作只能在叶节点中进行,非叶节点存储的是相邻子节点之间分隔值的副本,例如,某个元素的右子节点列表中最左边的值。
- 当一个列表变得满时(例如,有 n 个节点),该节点会被“拆分”,这意味着创建两个新节点并将分隔值传递给父节点。
B 树最初被描述为二叉搜索树的概括,其中二叉树是一个 2 节点 B 树,2 代表两个子节点,有一个 2-1 = 1 个键用于分隔这两个子节点。因此,3 节点有两个值用于分隔 3 个子节点,N 节点有 N 个子节点被 N-1 个键分隔。
经典的 B 树可以具有 N 节点内部节点和空的 2 节点叶节点,或者更方便地,子节点可以是值或指向下一个 N 节点的指针,因此它是一个联合。
B 树的主要思想是,首先创建一个根 N 节点,它可以容纳 N-1 个条目,但在第 N 个条目时,节点的键数量将用完,该节点可以拆分为两个大小为 N/2 的 N 节点,它们被一个单独的键 K 分隔,该键 K 等于右节点的最左键,因此任何键 K2 大于或等于 K 的条目都将进入右节点,小于 K 的条目都将进入左节点。当根节点拆分时,会创建一个新的根节点,它包含一个键以及一个左子节点和一个右子节点。由于有 N 个子节点,但只有 N-1 个条目,因此最左边的子节点被存储为一个单独的指针。如果最左边的指针拆分,则左半部分将成为新的最左边的指针,右半部分和分隔键将插入条目的开头。
另一种方法是 B+ 树,它在数据库系统中最常用,因为只有叶节点存储值,而内部节点只存储键和指向其他节点的指针,这限制了数据值的大小,因为指针的大小有限。这通常允许内部节点包含更多条目,从而能够适应一定大小的块,例如 4K 是一个常见的物理磁盘块大小。因此,如果一个 B+ 树内部节点与物理磁盘块对齐,那么由于它没有被缓存在内存块列表中,所以从磁盘读取一个大索引块的主要速率限制因素将减少到一个块读取。
B+ 树具有更大的内部节点,因此在理论上比等效的 B 树更宽且更短,B 树必须将所有节点都放入给定的物理块大小中,因此,总的来说,它是一个更快的索引,因为它的扇出更大,并且平均而言到达键的高度更低。
显然,这种扇出非常重要,也可以对块进行压缩,以增加在给定底层块大小中可以容纳的条目数量(底层层通常是文件系统块)。
大多数数据库系统使用 B+ 树算法,包括 postgresql、mysql、derbydb、firebird、许多 Xbase 索引类型等等。
许多文件系统也使用 B+ 树来管理它们的块布局(例如,xfs、NTFS 等等)。
Transwiki 提供了一个使用传统数组作为键列表和值列表的 B+ 树的 Java 实现。
下面是一个带有测试驱动程序的 B 树的示例,以及一个带有测试驱动程序的 B+ 树的示例。内存/磁盘管理没有包含在内,但可以在 哈希内存检查示例 中找到一个可用的黑客示例。
这个 B+ 树实现是基于 B 树实现的,它与 transwiki B+ 树的区别在于,它试图使用标准 Java 集合库中已经存在的 SortedMap 和 SortedSet 的语义。
因此,这个 B+ 实现的平面叶块列表不能包含不包含任何数据的块,因为排序依赖于条目的第一个键,所以需要创建一个叶块,并使用第一个条目填充它。
package btreemap;
import java.util.ArrayList;
import java.util.Collection;
import java.util.Collections;
import java.util.Comparator;
import java.util.List;
import java.util.Map;
import java.util.Set;
import java.util.SortedMap;
import java.util.TreeMap;
/** can't work without setting a comparator */
public class BTreeMap<K, V> implements SortedMap<K, V> {
private static final int NODE_SIZE = 100;
@Override
public Comparator<? super K> comparator() {
// TODO Auto-generated method stub
return comparator;
}
Comparator< ? super K> defaultComparator = new
Comparator< K>() {
@Override
public int compare(K o1, K o2) {
// TODO Auto-generated method stub
Comparable c1 = (Comparable)o1;
Comparable c2 = (Comparable)o2;
return c1.compareTo(c2);
}
};
Comparator<? super K> comparator = defaultComparator;
BTBlock<K, V> root = new BTBlock<K, V>(NODE_SIZE, comparator);
/**
*
* @param comparator
* - this is mandatory for the tree to work
*/
public void setComparator(Comparator<? super K> comparator) {
this.comparator = comparator;
root = new BTBlock<K, V>(NODE_SIZE, comparator);
}
/**
*
*
*
* @param <K>
* @param <V>
* the entry is associated with a right child block.
*
*/
static class BlockEntry<K, V> {
K k;
V v;
BTBlock left;
BlockEntry() {
}
BlockEntry(K k, V v) {
left = null;
this.k = k;
this.v = v;
}
}
/**
*
* - this represents the result of splitting a full block into
* a left block, and a right block, and a median key, the right
* block and the median key held in a BlockEntry structure as above.
* @param <K>
* @param <V>
* @param <V>g
*/
static class SplitRootEntry<K, V> {
BTBlock<K, V> right;
BlockEntry<K, V> entry;
SplitRootEntry(BlockEntry<K, V> entry, BTBlock<K, V> right) {
this.right = right;
this.entry = entry;
}
SplitRootEntry() {
super();
}
}
/**
* this is used to return a result of a possible split , during recursive
* calling.
*
*
*
* @param <K>
* @param <V>
*/
static class resultAndSplit<K, V> {
/**
* null , if there is no split.
*/
SplitRootEntry<K, V> splitNode;
V v;
resultAndSplit(V v) {
this.v = v;
}
resultAndSplit(SplitRootEntry<K, V> entry, V v) {
this.v = v;
this.splitNode = entry;
}
}
/**
* used to represent the insertion point after searching a block if compare
* is zero, then a match was found, and pos is the insertion entry if
* compare < 0 and pos == 0 , then the search ended up less than the
* leftmost entry else compare > 0 , and the search will be to the immediate
* right of pos.
*
*
*
*/
static class PosAndCompare {
int pos = 0;
int compare = 0;
}
static class BTBlock<K, V> {
List<BlockEntry<K, V>> entries;
BTBlock<K, V> rightBlock = null;
private int maxSz = 0;
Comparator<? super K> comparator;
Comparator<? super K> comparator() {
return comparator;
}
public BTBlock(int size, Comparator<? super K> c) {
entries = new ArrayList<BlockEntry<K, V>>();
maxSz = size;
this.comparator = c;
}
/**
* PosAndCompare usage: if compare is zero, then a match was found, and
* pos is the insertion entry if compare < 0 and pos == 0 , then the
* search ended up less than the leftmost entry else compare > 0 , and
* the search will be to the immediate right of pos.
*
*
*
*/
// private void blockSearch(K k, PosAndCompare pc) {
// for (int i = 0; i < entries.size(); ++i) {
// pc.compare = comparator.compare(k, entries.get(i).k);
// if (pc.compare == 0) {
// pc.pos = i;
// return;
// }
// if (pc.compare < 0 && i == 0) {
// pc.pos = 0;
// return;
// }
//
// if (pc.compare < 0) {
// pc.pos = i - 1;
// pc.compare = 1;
// return;
// }
//
// }
// pc.pos = entries.size() - 1;
// pc.compare = 1;
//
// // binary search, it's hard to get it right !
// // int left = 0;
// // int right = entries.size();
// //
// // while (left <= right && left < entries.size()) {
// // // pc.pos = (right - left) / 2 + left;
// // pc.pos = (left + right) / 2;
// // pc.compare = comparator().compare(k, entries.get(pc.pos).k);
// // if (pc.compare < 0) {
// // right = pc.pos - 1;
// // } else if (pc.compare > 0) {
// // left = pc.pos + 1;
// // } else {
// // return;
// // }
// // }
// //
// // BlockEntry<K, V> e = new BlockEntry<K, V>(k, null);
// // pc.pos = Collections.binarySearch(entries, e, cmp);
//
// }
Comparator<BlockEntry<K, V>> cmp = new Comparator<BlockEntry<K, V>>() {
@Override
public int compare(BlockEntry<K, V> o1, BlockEntry<K, V> o2) {
// TODO Auto-generated method stub
return comparator.compare(o1.k, o2.k);
}
};
resultAndSplit<K, V> put(K k, V v) {
V v2;
if (entries.size() == 0) {
entries.add(new BlockEntry<K, V>(k, v));
return new resultAndSplit<K, V>(v);
} else {
// PosAndCompare pc = new PosAndCompare();
BlockEntry<K, V> e = new BlockEntry<K, V>(k, v);
int res = Collections.binarySearch(entries, e, cmp);
int index = -res - 1;
// blockSearch(k, pc);
// a match
if (res >= 0) {
v2 = entries.get(res).v;
entries.get(res).v = v;
return new resultAndSplit<K, V>(v2);
}
// follow leftBlock if search is to left of first entry
if (index == entries.size() && rightBlock != null) {
resultAndSplit<K, V> result = rightBlock.put(k, v);
if (result.splitNode != null) {
rightBlock = result.splitNode.right;
entries.add(result.splitNode.entry);
}
} else if (index == entries.size() && rightBlock == null
&& entries.size() == maxSz) {
rightBlock = new BTBlock<K, V>(this.maxSz, comparator);
resultAndSplit<K, V> result = rightBlock.put(k, v);
} else if (index < entries.size()
&& entries.get(index).left != null) {
// follow right block if it exists
resultAndSplit<K, V> result = entries.get(index).left.put(
k, v);
if (result.splitNode != null) {
entries.get(index).left = result.splitNode.right;
// add to the left
entries.add(index, result.splitNode.entry);
}
} else {
// add to the left
entries.add(index, e);
}
// check if overflowed block , split if it has.
if (entries.size() > maxSz) {
int mid = entries.size() / 2;
// copy right half to new entries list.
List<BlockEntry<K, V>> leftEntries = new ArrayList<BlockEntry<K, V>>();
for (int i = 0; i < mid; ++i) {
leftEntries.add(entries.get(i));
}
BlockEntry<K, V> centreEntry = entries.get(mid);
BTBlock<K, V> leftBlock = new BTBlock<K, V>(maxSz,
comparator);
leftBlock.entries = leftEntries;
// the median entry's left block is the new left block's
// leftmost block
leftBlock.rightBlock = centreEntry.left;
// the new right block becomes the right block
centreEntry.left = leftBlock;
// reduce the old block's entries into its left half of
// entries.
ArrayList<BlockEntry<K, V>> newEntries = new ArrayList<BlockEntry<K, V>>();
for (int i = mid + 1; i < entries.size(); ++i)
newEntries.add(entries.get(i));
this.entries = newEntries;
// create a return object, with the reduced old block as the
// left block
// and the median entry with the new right block attached
SplitRootEntry<K, V> split = new SplitRootEntry<K, V>(
centreEntry, this);
// the keyed value didn't exist before , so null
return new resultAndSplit<K, V>(split, null);
}
return new resultAndSplit<K, V>(v);
}
}
V get(K k) {
if (entries.size() == 0)
return null;
BlockEntry<K, V> e = new BlockEntry<K, V>(k, null);
int res = Collections.binarySearch(entries, e, cmp);
int index = -res - 1;
if (res >= 0) {
return entries.get(res).v;
}
if (index == entries.size() && rightBlock != null) {
return rightBlock.get(k);
} else if (index < entries.size()
&& entries.get(index).left != null) {
return (V) entries.get(index).left.get(k);
} else
return null;
}
void getRange(SortedMap map, K k1, K k2) {
BlockEntry<K, V> e = new BlockEntry<K, V>(k1, null);
int res = Collections.binarySearch(entries, e, cmp);
int index = -res - 1;
BlockEntry<K, V> e2 = new BlockEntry<K, V>(k2, null);
int res2 = Collections.binarySearch(entries, e2, cmp);
int index2 = -res2 - 1;
int from = res >= 0 ? res : index;
int to = res2 >= 0 ? res2 : index2;
for (int i = from; i <= to; ++i) {
if (i < entries.size() && (i > from || res < 0)
&& entries.get(i).left != null) {
entries.get(i).left.getRange(map, k1, k2);
// if (pc2.pos == pc.pos)
// break;
}
if (i < to || res2 >= 0)
map.put(entries.get(i).k, entries.get(i).v);
if (i == entries.size() && rightBlock != null) {
rightBlock.getRange(map, k1, k2);
}
}
}
K headKey() {
if (rightBlock != null) {
return rightBlock.headKey();
}
return entries.get(0).k;
}
K tailKey() {
int i = entries.size() - 1;
if (entries.get(i).left != null) {
return (K) entries.get(i).left.tailKey();
}
return entries.get(i).k;
}
void show(int n) {
showTabs(n);
for (int i = 0; i < entries.size(); ++i) {
BlockEntry<K, V> e = entries.get(i);
System.err.print("#" + i + ":(" + e.k + ":" + e.v + ") ");
}
System.err.println();
showTabs(n);
if (rightBlock != null) {
System.err.print("Left Block\n");
rightBlock.show(n + 1);
} else {
System.err.println("No Left Block");
}
for (int i = 0; i < entries.size(); ++i) {
BlockEntry<K, V> e = entries.get(i);
showTabs(n);
if (e.left != null) {
System.err.println("block right of #" + i);
e.left.show(n + 1);
} else {
System.err.println("No block right of #" + i);
}
}
showTabs(n);
System.err.println("End of Block Info\n\n");
}
private void showTabs(int n) {
// TODO Auto-generated method stub
for (int i = 0; i < n; ++i) {
System.err.print(" ");
}
}
}
@Override
public SortedMap<K, V> subMap(K fromKey, K toKey) {
TreeMap<K, V> map = new TreeMap<K, V>();
root.getRange(map, fromKey, toKey);
return map;
}
@Override
public SortedMap<K, V> headMap(K toKey) {
// TODO Auto-generated method stub
return subMap(root.headKey(), toKey);
};
@Override
public SortedMap<K, V> tailMap(K fromKey) {
// TODO Auto-generated method stub
return subMap(fromKey, root.tailKey());
}
@Override
public K firstKey() {
// TODO Auto-generated method stub
return root.headKey();
}
@Override
public K lastKey() {
// TODO Auto-generated method stub
return root.tailKey();
}
@Override
public int size() {
// TODO Auto-generated method stub
return 0;
}
@Override
public boolean isEmpty() {
// TODO Auto-generated method stub
return false;
}
@Override
public boolean containsKey(Object key) {
// TODO Auto-generated method stub
return get(key) != null;
}
@Override
public boolean containsValue(Object value) {
// TODO Auto-generated method stub
return false;
}
@Override
public V get(Object key) {
// TODO Auto-generated method stub
return root.get((K) key);
}
@Override
public V put(K key, V value) {
resultAndSplit<K, V> b = root.put(key, value);
if (b.splitNode != null) {
root = new BTBlock<K, V>(root.maxSz, root.comparator);
root.rightBlock = b.splitNode.right;
root.entries.add(b.splitNode.entry);
}
return b.v;
}
@Override
public V remove(Object key) {
// TODO Auto-generated method stub
return null;
}
@Override
public void putAll(Map<? extends K, ? extends V> m) {
// TODO Auto-generated method stub
}
@Override
public void clear() {
// TODO Auto-generated method stub
}
@Override
public Set<K> keySet() {
// TODO Auto-generated method stub
return null;
}
@Override
public Collection<V> values() {
// TODO Auto-generated method stub
return null;
}
@Override
public Set<java.util.Map.Entry<K, V>> entrySet() {
// TODO Auto-generated method stub
return null;
}
}
package btreemap;
import java.util.ArrayList;
import java.util.Comparator;
import java.util.List;
import java.util.Random;
public class TestBtree {
private static final int N = 50000;
public static void main(String[] args) {
BTreeMap<Integer, Integer> map = new BTreeMap<Integer , Integer>();
Random r = new Random();
ArrayList<Integer> t = new ArrayList<Integer>();
Comparator<Integer> comparator = new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
// TODO Auto-generated method stub
return o1.intValue() - o2.intValue();
}
};
map.setComparator(comparator);
List<Integer> testVals = new ArrayList<Integer>();
for (int i =0 ; i < N ; ++i) {
testVals.add(i);
}
for (int i = 0; i < N; ++i ) {
int x = r.nextInt(testVals.size());
x = testVals.remove(x);
//int x=i;
t.add(x);
map.put(x, x);
}
System.err.println("output " + N + " vals");
map.root.show(0);
for (int i = 0; i < N; ++i) {
int x = t.get(i);
if ( x != map.get(x))
System.err.println("Expecting " + x + " got " + map.get(x));
}
System.err.println("Checked " + N + " entries");
}
}
实验包括计时运行(例如,time java -cp . btreemap.BPlusTreeTest1),使用外部块大小 + 1 大小的叶块大小,这样它基本上只是底层的条目 TreeMap,与使用 400 个内部节点大小和 200 个外部节点大小相比。其他实验包括使用 SkipListMap 而不是 TreeMap。
package btreemap;
import java.util.Collection;
import java.util.Comparator;
import java.util.Map;
import java.util.Set;
import java.util.SortedMap;
import java.util.SortedSet;
import java.util.TreeMap;
import java.util.TreeSet;
/**
* a B+ tree, where leaf blocks contain key-value pairs and
* internal blocks have keyed entries pointing to other internal blocks
* or leaf blocks whose keys are greater than or equal to the associated key.
*
* @author syan
*
* @param <K> key type implements Comparable
* @param <V> value type
*/
public class BPlusTreeMap<K, V> implements SortedMap<K, V> {
private int maxInternalBlockSize;
BPlusAnyBlock<K, V> root;
private int maxExternalSize;
BPlusTreeMap(int maxInternalSize, int maxExternalSize) {
this.maxInternalBlockSize = maxInternalSize;
this.maxExternalSize = maxExternalSize;
}
static class SplitOrValue<K, V> {
V v;
K k;
BPlusAnyBlock<K, V> left, right;
boolean split;
public boolean isSplit() {
return split;
}
public void setSplit(boolean split) {
this.split = split;
}
public SplitOrValue(V value) {
v = value;
setSplit(false);
}
public SplitOrValue(BPlusAnyBlock<K, V> left2,
BPlusAnyBlock<K, V> bPlusBlock) {
left = left2;
right = bPlusBlock;
k = right.firstKey();
setSplit(true);
// System.err.printf("\n\n** split occured %s**\n\n", bPlusBlock
// .getClass().getSimpleName());
}
}
static abstract class BPlusAnyBlock<K, V> {
public abstract SplitOrValue<K, V> put(K k, V v);
abstract SplitOrValue<K, V> splitBlock();
public abstract V get(K k);
public abstract boolean isEmpty();
public abstract K firstKey();
}
SortedSet<BPlusLeafBlock<K, V>> blockList = getLeafBlockSet();
SortedSet<BPlusLeafBlock<K, V>> getLeafBlockSet() {
// return new ConcurrentSkipListSet<BPlusLeafBlock<K, V>>();
return new TreeSet<BPlusLeafBlock<K, V>>();
}
static class BPlusLeafBlock<K, V> extends BPlusAnyBlock<K, V> implements
Comparable<BPlusLeafBlock<K, V>> {
SortedMap<K, V> entries = getEntryCollection();
static <K, V> SortedMap<K, V> getEntryCollection() {
return new TreeMap<K, V>();
}
int maxSize;
private BPlusTreeMap<K, V> owner;
public boolean isEmpty() {
return entries.isEmpty();
}
public BPlusLeafBlock(BPlusTreeMap<K, V> bPlusTreeMap,
SortedMap<K, V> rightEntries) {
this.owner = bPlusTreeMap;
maxSize = owner.maxExternalSize;
entries = rightEntries;
}
public SplitOrValue<K, V> put(K k, V v) {
V v2 = entries.put(k, v);
if (entries.size() >= maxSize)
return splitBlock();
else
return new SplitOrValue<K, V>(v2);
}
public SplitOrValue<K, V> splitBlock() {
SortedMap<K, V> leftEntries = getEntryCollection();
SortedMap<K, V> rightEntries = getEntryCollection();
int i = 0;
for (Entry<K, V> e : entries.entrySet()) {
// System.out.println(this.getClass().getSimpleName() +
// " split entry " + e.getKey());
if (++i <= maxSize / 2)
leftEntries.put(e.getKey(), e.getValue());
else
rightEntries.put(e.getKey(), e.getValue());
}
BPlusLeafBlock<K, V> right = createBlock(rightEntries);
// System.out.println("finished block split");
// System.out.println("\nleft block");
// for (K ik : leftEntries.keySet()) {
// System.out.print(ik + " ");
// }
// System.out.println("\nright block");
// for (K ik : right.entries.keySet()) {
// System.out.print(ik + " ");
// }
// System.out.println("\n");
this.entries = leftEntries;
return new SplitOrValue<K, V>(this, right);
}
private BPlusLeafBlock<K, V> createBlock(SortedMap<K, V> rightEntries) {
return owner.createLeafBlock(rightEntries);
}
@Override
public V get(K k) {
return entries.get(k);
}
@Override
public int compareTo(BPlusLeafBlock<K, V> o) {
return ((Comparable<K>) entries.firstKey()).compareTo(o.entries
.firstKey());
}
@Override
public K firstKey() {
return entries.firstKey();
}
}
static class BPlusBranchBlock<K, V> extends BPlusAnyBlock<K, V> {
SortedMap<K, BPlusAnyBlock<K, V>> entries = createInternalBlockEntries();
int maxSize;
private BPlusAnyBlock<K, V> left;
public boolean isEmpty() {
return entries.isEmpty();
}
public BPlusBranchBlock(int maxSize2) {
this.maxSize = maxSize2;
}
public SplitOrValue<K, V> put(K k, V v) {
BPlusAnyBlock<K, V> b = getBlock(k);
SplitOrValue<K, V> sv = b.put(k, v);
if (sv.isSplit()) {
entries.put(sv.k, sv.right);
if (entries.size() >= maxSize)
sv = splitBlock();
else
sv = new SplitOrValue<K, V>(null);
}
return sv;
}
BPlusAnyBlock<K, V> getBlock(K k) {
assert (entries.size() > 0);
BPlusAnyBlock<K, V> b = entries.get(k);
if (b == null) {
// headMap returns less than k
SortedMap<K, BPlusAnyBlock<K, V>> head = entries.headMap(k);
if (head.isEmpty()) {
b = left;
// System.out.println("for key " + k
// + " getting from leftmost block");
// showEntries();
} else {
b = entries.get(head.lastKey());
// System.out.println("for key " + k
// + " getting from block with key " + head.lastKey());
// showEntries();
}
}
assert (b != null);
return b;
}
public void showEntries() {
System.out.print("entries = ");
for (K k : entries.keySet()) {
System.out.print(k + " ");
}
System.out.println();
}
public SplitOrValue<K, V> splitBlock() {
Set<Entry<K, BPlusAnyBlock<K, V>>> ee = entries.entrySet();
int i = 0;
BPlusBranchBlock<K, V> right = new BPlusBranchBlock<K, V>(maxSize);
SortedMap<K, BPlusAnyBlock<K, V>> leftEntries = createInternalBlockEntries();
for (Entry<K, BPlusAnyBlock<K, V>> e : ee) {
// System.out.print("split check " + e.getKey() + ":"
// );
if (++i <= maxSize / 2)
leftEntries.put(e.getKey(), e.getValue());
else
right.entries.put(e.getKey(), e.getValue());
}
// System.out.println("\n");
this.entries = leftEntries;
return new SplitOrValue<K, V>(this, right);
}
private SortedMap<K, BPlusAnyBlock<K, V>> createInternalBlockEntries() {
return new TreeMap<K, BPlusAnyBlock<K, V>>();
}
@Override
public V get(K k) {
BPlusAnyBlock<K, V> b = getBlock(k);
return b.get(k);
}
@Override
public K firstKey() {
return entries.firstKey();
}
}
@Override
public SortedMap<K, V> subMap(K fromKey, K toKey) {
TreeMap<K, V> map = new TreeMap<K, V>();
BPlusLeafBlock<K, V> b1 = getLeafBlock(fromKey);
BPlusLeafBlock<K, V> b2 = getLeafBlock(toKey);
SortedSet<BPlusLeafBlock<K, V>> range = blockList.subSet(b1, b2);
for (BPlusLeafBlock<K, V> b : range) {
SortedMap<K, V> m = b.entries.subMap(fromKey, toKey);
map.putAll(m);
}
return map;
}
private BPlusLeafBlock<K, V> getLeafBlock(K key) {
BPlusAnyBlock<K, V> b1;
b1 = root;
while (b1 instanceof BPlusBranchBlock<?, ?>) {
b1 = ((BPlusBranchBlock<K, V>) b1).getBlock(key);
}
return (BPlusLeafBlock<K, V>) b1;
}
public BPlusLeafBlock<K, V> createLeafBlock(SortedMap<K, V> rightEntries) {
BPlusLeafBlock<K, V> b = new BPlusLeafBlock<K, V>(this, rightEntries);
blockList.add(b);
return b;
}
@Override
public SortedMap<K, V> headMap(K toKey) {
return subMap(firstKey(), toKey);
};
@Override
public SortedMap<K, V> tailMap(K fromKey) {
return subMap(fromKey, lastKey());
}
@Override
public K firstKey() {
return blockList.first().entries.firstKey();
}
@Override
public K lastKey() {
return blockList.last().entries.lastKey();
}
@Override
public int size() {
return (int) getLongSize();
}
private long getLongSize() {
long i = 0;
for (BPlusLeafBlock<K, V> b : blockList) {
i += b.entries.size();
}
return i;
}
@Override
public boolean isEmpty() {
return root.isEmpty();
}
@Override
public boolean containsKey(Object key) {
return get(key) != null;
}
@Override
public boolean containsValue(Object value) {
return false;
}
@Override
public V get(Object key) {
return (V) root.get((K) key);
}
@Override
public V put(K key, V value) {
if (root == null) {
SortedMap<K, V> entries = BPlusLeafBlock.getEntryCollection();
entries.put(key, value);
root = createLeafBlock(entries);
return null;
}
SplitOrValue<K, V> result = root.put(key, value);
if (result.isSplit()) {
BPlusBranchBlock<K, V> root = new BPlusBranchBlock<K, V>(
maxInternalBlockSize);
root.left = result.left;
root.entries.put(result.k, result.right);
this.root = root;
}
return result.v;
}
@Override
public V remove(Object key) {
return null;
}
@Override
public void putAll(Map<? extends K, ? extends V> m) {
for (K k : m.keySet()) {
put(k, m.get(k));
}
}
@Override
public void clear() {
}
@Override
public Set<K> keySet() {
TreeSet<K> kk = new TreeSet<K>();
for (BPlusLeafBlock<K, V> b : blockList) {
kk.addAll(b.entries.keySet());
}
return kk;
}
@Override
public Collection<V> values() {
// TODO Auto-generated method stub
return null;
}
@Override
public Set<java.util.Map.Entry<K, V>> entrySet() {
// TODO Auto-generated method stub
return null;
}
@Override
public Comparator<? super K> comparator() {
// TODO Auto-generated method stub
return null;
}
public void showLeaves() {
for (BPlusLeafBlock<K, V> b : blockList) {
System.out.println("Block");
for (Entry<K, V> e : b.entries.entrySet()) {
System.out.print(e.getKey() + ":" + e.getValue() + " ");
}
System.out.println();
}
}
}
package btreemap;
import java.util.ArrayList;
import java.util.Comparator;
import java.util.List;
import java.util.Random;
/** driver program to test B+ tree */
public class BPlusTreeTest1 {
private static final int N = 1200000;
public static void main(String[] args) {
BPlusTreeMap<Integer, Integer> map = new BPlusTreeMap<Integer, Integer>(
400, 200 );// 5000002);
Random r = new Random();
ArrayList<Integer> t = new ArrayList<Integer>();
Comparator<Integer> comparator = new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
// TODO Auto-generated method stub
return o1.intValue() - o2.intValue();
}
};
List<Integer> testVals = new ArrayList<Integer>();
for (int i = 0; i < N; ++i) {
testVals.add(i);
}
for (int i = 0; i < N; ++i) {
int x = r.nextInt(N);
int z = testVals.set(x, testVals.get(0));
testVals.set(0, z);
}
for (int i = 0; i < N; ++i) {
map.put(testVals.get(i), testVals.get(i));
showProgress("put", testVals, i);
}
System.err.println("output " + N + " vals");
try {
for (int i = 0; i < N; ++i) {
showProgress("get", testVals, i);
int x = testVals.get(i);
if (x != map.get(x))
System.err.println("Expecting " + x + " got " + map.get(x));
}
System.err.println("\nChecked " + N + " entries");
} catch (Exception e) {
// TODO: handle exception
e.printStackTrace();
map.showLeaves();
}
}
private static void showProgress(String label, List<Integer> testVals, int i) {
if (i % (N / 1000) == 0) {
System.out.printf("%s %d:%d; ", label, i, testVals.get(i));
if (i % (N / 10100) == 0)
System.out.println();
}
}
}
二叉树的不变性是,相对于插入键,左小于右。例如,对于一个有序的键,ord(L) < ord(R)。但是,这并不能决定节点之间的关系,左旋转和右旋转不会影响上述情况。因此,可以施加另一个顺序。如果顺序是随机的,它很可能抵消普通二叉树的任何倾斜,例如,当按顺序插入一个已经排序的输入时。
以下是一个 Java 示例实现,包括一个普通二叉树删除代码示例。
import java.util.Iterator;
import java.util.LinkedList;
import java.util.Random;
public class Treap1<K extends Comparable<K>, V> {
public Treap1(boolean test) {
this.test = test;
}
public Treap1() {}
boolean test = false;
static Random random = new Random(System.currentTimeMillis());
class TreapNode {
int priority = 0;
K k;
V val;
TreapNode left, right;
public TreapNode() {
if (!test) {
priority = random.nextInt();
}
}
}
TreapNode root = null;
void insert(K k, V val) {
root = insert(k, val, root);
}
TreapNode insert(K k, V val, TreapNode node) {
TreapNode node2 = new TreapNode();
node2.k = k;
node2.val = val;
if (node == null) {
node = node2;
} else if (k.compareTo(node.k) < 0) {
node.left = insert(k, val, node.left);
} else {
node.right = insert(k, val, node.right);
}
if (node.left != null && node.left.priority > node.priority) {
// left rotate
TreapNode tmp = node.left;
node.left = node.left.right;
tmp.right = node;
node = tmp;
} else if (node.right != null && node.right.priority > node.priority) {
// right rotate
TreapNode tmp = node.right;
node.right = node.right.left;
tmp.left = node;
node = tmp;
}
return node;
}
V find(K k) {
return findNode(k, root);
}
private V findNode(K k, Treap1<K, V>.TreapNode node) {
if (node == null)
return null;
if (k.compareTo(node.k) < 0) {
return findNode(k, node.left);
} else if (k.compareTo(node.k) > 0) {
return findNode(k, node.right);
} else {
return node.val;
}
}
static class Deleted {
boolean success = false;
}
boolean delete(K k) {
Deleted del = new Deleted();
root = deleteNode(k, root, del);
return del.success;
}
private Treap1<K, V>.TreapNode deleteNode(K k, Treap1<K, V>.TreapNode node, Deleted del) {
if (node == null) {
return null;
} else if (k.compareTo(node.k) < 0) {
node.left = deleteNode(k, node.left, del) ;
} else if (k.compareTo(node.k) > 0) {
node.right = deleteNode(k, node.right, del);
// k.compareTo(node.k) == 0
} else if ( node.left == null ) {
del.success = true;
return node.right;
} else if ( node.right == null) {
del.success = true;
return node.left;
} else if (node.left !=null && node.right != null){
/*
// left rotate and all delete on left subtree
TreapNode tmp = node.right;
node.right = node.right.left;
tmp.left = node;
node = tmp;
node.left = deleteNode(k , node.left, del);
*/
// more standard method ? doesn't disturb tree structure as much
// find leftmost descendant of the right child node and replace contents
TreapNode n2 = node.right;
TreapNode previous2 = null;
while (n2.left != null) {
previous2 = n2;
n2 = n2.left;
}
if (previous2 != null) {
previous2.left = n2.right;
//n2 has no parent link, orphaned
} else {
node.right = n2.right;
//n2 has no parent link, orphaned
}
node.k = n2.k;
node.val = n2.val;
del.success = true;
// once n2 out of scope, the orphaned node at n2 will be garbage collected,
}
return node;
}
public static void main(String[] args) {
LinkedList<Integer> dat = new LinkedList<Integer>();
for (int i = 0; i < 15000; ++i) {
dat.add(i);
}
testNumbers(dat, true); // no random priority balancing
testNumbers(dat, false);
}
private static void testNumbers(LinkedList<Integer> dat,
boolean test) {
Treap1<Integer, Integer> treap = new Treap1<>(test);
for (Integer integer : dat) {
treap.insert(integer, integer);
}
long t1 = System.currentTimeMillis();
Iterator<Integer> desc = dat.iterator();
int found = 0;
while (desc.hasNext()) {
Integer j = desc.next();
Integer i = treap.find(j);
if (j.equals(i)) {
++found;
}
}
long t2 = System.currentTimeMillis();
System.out.println("found = " + found + " in " + (t2 - t1));
System.out.println("test delete");
int deleted = 0;
for (Integer integer : dat) {
if (treap.delete(integer))
++deleted;
}
System.out.println("Deleted = " + deleted);
}
}
- William Ford 和 William Tapp。使用STL的C++数据结构。第 2 版。新泽西州上萨德尔河:普伦蒂斯·霍尔,2002 年。
以下是堆的一些定义
堆是一个数组,其中存在父子关系,子节点的索引是父节点索引的 2 倍或 2 倍加 1,子节点在父节点之后有一个顺序,这由堆的客户端程序注入的某种具体排序方案决定。维护排序不变式在堆发生变化后至关重要。一些人(Sedgewick 和 Wayne)创造了“上浮”和“下沉”这两个术语,其中维护不变式包括一个违反不变式的项目向上浮动到排序较低的子节点之上,然后下沉到排序较高的子节点之下,因为可能存在两个子节点,因此一个项目可以浮动到排序较低的子节点之上,而另一个子节点的排序仍然更高。
堆是一种高效的半排序数据结构,用于存储可排序数据的集合。最小堆支持两种操作
INSERT(heap, element) element REMOVE_MIN(heap)
(我们讨论最小堆,但最小堆和最大堆之间没有真正区别,除了比较的解释方式。)
本章将专门讨论二叉堆,尽管存在不同类型的堆。在大多数情况下,术语二叉堆和堆可以互换使用。堆可以看作是一棵具有父节点和子节点的树。堆和二叉树之间的主要区别在于堆属性。为了使一种数据结构被认为是堆,它必须满足以下条件(堆属性)
- 如果A和B是堆中的元素,并且B是A的子节点,那么 key(A) ≤ key(B)。
(此属性适用于最小堆。最大堆的比较将相反)。这意味着最小键将始终保留在顶部,而更大的值将位于其下方。由于这个事实,堆用于实现优先级队列,这允许快速访问优先级最高的项目。以下是一个最小堆的示例

堆是用一个从 1 到 N 索引的数组实现的,其中 N 是堆中元素的数量。
在任何时候,堆都必须满足堆属性
array[n] <= array[2*n] // parent element <= left child
和
array[n] <= array[2*n+1] // parent element <= right child
只要索引在数组边界内。
我们将证明array[1]是堆中的最小元素。我们通过观察如果其他元素小于第一个元素,则会产生矛盾来证明这一点。假设array[i]是第一个最小值的实例,其中对于所有j < i,array[j] > array[i],并且i >= 2。但是根据堆不变式数组,array[floor(i/2)] <= array[i]:这是一个矛盾。
因此,很容易计算MIN(heap)
MIN(heap)
return heap.array[1];
要移除最小元素,我们必须调整堆以填充heap.array[1]。这个过程被称为渗透。基本上,我们将空洞从节点 i 移动到节点2i或2i+1。如果我们选择这两个节点中的最小值,则堆不变式将得到维护;假设array[2i] < array[2i+1]。然后array[2i]将被移动到array[i],在2i处留下一个空洞,但是移动后array[i] < array[2i+1],因此堆不变式得到维护。在某些情况下,2i+1将超出数组边界,我们被迫渗透2i。在其他情况下,2i也在边界之外:在这种情况下,我们已经完成。
因此,以下是最小堆的移除算法
#define LEFT(i) (2*i)
#define RIGHT(i) (2*i + 1)
REMOVE_MIN(heap)
{
savemin=arr[1];
arr[1]=arr[--heapsize];
i=1;
while(i<heapsize){
minidx=i;
if(LEFT(i)<heapsize && arr[LEFT(i)] < arr[minidx])
minidx=LEFT(i);
if(RIGHT(i)<heapsize && arr[RIGHT(i)] < arr[minidx])
minidx=RIGHT(i);
if(minidx!=i){
swap(arr[i],arr[minidx]);
i=minidx;
}
else
break;
}
}
为什么这有效?
If there is only 1 element ,heapsize becomes 0, nothing in the array is valid. If there are 2 elements , one min and other max, you replace min with max. If there are 3 or more elements say n, you replace 0th element with n-1th element. The heap property is destroyed. Choose the 2 children of root and check which is the minimum. Choose the minimum between them, swap it. Now subtree with swapped child is loose heap property. If no violations break.
INSERT 存在类似的策略:只需将元素附加到数组,然后通过交换修复堆不变式。例如,如果我们刚刚附加了元素 N,那么唯一可能的不变式违反涉及该元素,特别是如果,那么这两个元素必须交换,现在唯一可能的不变式违反是在…之间
array[floor(N/4)] and array[floor(N/2)]
我们继续迭代,直到 N=1 或直到不变式得到满足。
INSERT(heap, element)
append(heap.array, element)
i = heap.array.length
while (i > 1)
{
if (heap.array[i/2] <= heap.array[i])
break;
swap(heap.array[i/2], heap.array[i]);
i /= 2;
}
Merge-heap: it would take two max/min heap and merge them and return a single heap. O(n) time. Make-heap: it would also be nice to describe the O(n) make-heap operation Heap sort: the structure can actually be used to efficiently sort arrays
Make-heap 将使用一个名为 heapify 的函数
//Element is a data structure//
Make-heap(Element Arr[],int size)
{
for(j=size/2;j>0;j--)
{
Heapify(Arr,size,j);
}
}
Heapify(Element Arr[],int size,int t)
{
L=2*t;
R=2*t+1;
if(L<size )
{
mix=minindex(Arr,L,t);
if(R<=size)
mix=minindex(Arr,R,mix);
}
else
mix=t;
if(mix!=t)
{
swap(mix,t);
Heapify(Arr,size,mix);
}
}
minindex 返回较小元素的索引
在 2009 年,OzSort 赢得了较小的排序基准测试,它有一篇论文清晰地描述了如何使用优先级堆作为排序机器来生成大型(内部)排序部分的合并部分。如果一个排序部分占用 M 个内存,排序问题是 k x M 大小,那么每次取 k 个部分中每个部分大小为 M/k 的连续部分,这样它们就适合 M 个内存(k * M/k = M),并从 k 个部分的每个部分中取第一个元素来创建一个 k 大小的优先级队列,当顶部元素被移除并写入输出缓冲区时,从相应的部分取下一个元素。这意味着元素可能需要与它们所属部分的标签相关联。当一个 M/k 大小的部分用完时,从磁盘上存储的原始排序部分中加载下一个 M/k 大小的迷你部分。继续执行,直到磁盘上 k 个部分中的所有迷你部分都已用尽。
(作为管道以填补磁盘操作延迟的示例,存在两个输出缓冲区,因此当一个输出缓冲区已满时,一个缓冲区写入磁盘,而另一个缓冲区被填充。)
这篇论文表明,优先级堆比二叉树更直接,因为元素作为 k 路合并的排队机制不断被删除和添加,并且在对超过内部内存存储的大型数据集进行排序时具有实际应用价值。
一个图是一个结构,它包含一组顶点和一组边。边是一对顶点。这两个顶点称为边的端点。图在计算机科学中无处不在。它们用于对现实世界系统进行建模,例如互联网(每个节点代表一个路由器,每条边代表路由器之间的连接);航空连接(每个节点是一个机场,每条边是航班);或城市道路网络(每个节点代表一个交叉路口,每条边代表一个街区)。计算机图形中的线框图是图的另一个例子。
图可以是无向的,也可以是有向的。直观地说,无向边模拟其端点之间的“双向”或“双工”连接,而有向边是一路连接,通常绘制为箭头。有向边通常称为弧。在数学上,无向边是一对无序顶点,弧是一对有序顶点。例如,道路网络可以建模为有向图,其中单行道由端点之间相应方向上的箭头表示,双行道由一对平行有向边表示,在端点之间两个方向上都走。你可能会问,为什么不使用单个无向边来表示双行道。从理论上讲,这没有问题,但从实际编程的角度来看,坚持使用所有有向边或所有无向边通常更简单、更不易出错。
一个无向图最多可以有条边(每对无序顶点一条),而有向图最多可以有条边(每对有序顶点一条)。如果图的边数远少于这个数(通常为条边),则称为稀疏图;如果图的边数接近条边,则称为稠密图。多重图可以在同一对顶点之间拥有多条边。例如,如果要对航空航班进行建模,则两个城市之间可能存在多个航班,这些航班在一天中的不同时间发生。
图中的路径是一系列顶点,使得相邻顶点之间存在边或弧。如果,则该路径称为回路。无向无环图等效于无向树。有向无环图称为DAG。它不一定是树。
节点和边通常具有关联的信息,例如标签或权重。例如,在航空航班图中,节点可能用相应机场的名称标记,边可能具有等于飞行时间的权重。流行的游戏“凯文·贝肯的六度分离”可以用带标签的无向图来建模。每个演员都成为一个节点,用演员的姓名标记。当两个演员在某部电影中一起出现时,节点之间通过边连接。我们可以用电影的名称标记这条边。确定演员是否与凯文·贝肯之间隔着六步或更少的步骤,相当于在图中找到一条长度最多为六的路径,连接贝肯的顶点和另一个演员的顶点。(这可以通过在配套算法书中找到的广度优先搜索算法来完成。弗吉尼亚大学的贝肯神谕实际上已经实现了这种算法,并且可以通过几次点击告诉你从任何演员到凯文·贝肯的路径[1]。)
有向图
[edit | edit source]
具有一个端点在给定顶点上的边的数量称为该顶点的度数。在有向图中,指向给定顶点的边的数量称为其入度,而指向该顶点的边的数量称为其出度。通常,我们可能希望能够区分不同的节点和边。我们可以将标签与它们中的任何一个相关联。我们称这样的图带标签的。
有向图操作
make-graph(): graph- 创建一个新的图,最初没有节点或边。
make-vertex(graph G, element value): vertex- 创建一个新的顶点,具有给定的值。
make-edge(vertex u, vertex v): edge- 在u和v之间创建一条边。在有向图中,边将从u流向v。
get-edges(vertex v): edge-set- 返回从v流出的边的集合。
get-neighbors(vertex v): vertex-set- 返回连接到v的顶点的集合。
无向图
[edit | edit source]
在有向图中,边从一个顶点指向另一个顶点,而在无向图中,边只是连接两个顶点。我们可以向前或向后移动。这是一个双向图。
我们可能还想将某些成本或权重与边的遍历相关联。 当我们添加此信息时,图被称为**加权图**。 加权图的一个例子是国家首都之间的距离。
有向图和无向图都可以是加权的。 加权图上的操作与在创建边时添加权重参数相同。
加权图操作(无向/有向图操作的扩展)
make-edge(顶点u,顶点v,权重w):边- 在u和v之间创建一条权重为w的边。 在有向图中,边将从u流向v。
邻接矩阵是表示图的两种常用方法之一。 邻接矩阵显示哪些节点是相邻的。 如果两个节点之间有一条边连接,则这两个节点是相邻的。 在有向图的情况下,如果节点与节点相邻,则从到有一条边。 换句话说,如果与相邻,您可以通过遍历一条边从到达。 对于具有个节点的给定图,邻接矩阵将具有的维度。 对于无权图,邻接矩阵将用布尔值填充。
对于任何给定节点,您可以通过查看邻接矩阵的第行来确定其相邻节点。 处的真值表示从节点到节点有一条边,而假值表示没有边。 在无向图中,和的值将相等。 在加权图中,布尔值将被连接两个节点的边的权重替换,并使用一个特殊值表示边的不存在。
邻接矩阵的内存使用量为。
邻接表是另一种常见的图表示方法。有许多方法可以实现这种邻接表示。一种方法是让图维护一个列表列表,其中第一个列表是对应于图中每个节点的索引列表。这些中的每一个都引用另一个存储与该节点相邻的每个节点的索引的列表。在该列表中,将每个链接的权重与相邻节点关联起来也可能是有用的。
示例:一个无向图包含四个节点 1、2、3 和 4。1 与 2 和 3 相连。2 与 3 相连。3 与 4 相连。
1 - [2, 3]
2 - [1, 3]
3 - [1, 2, 4]
4 - [3]
将图中所有节点的列表存储在哈希表中可能会有用。然后键将对应于每个节点的索引,而值将是对相邻节点索引列表的引用。
另一种实现可能要求每个节点保留其相邻节点的列表。
在理想情况下,我们将完全了解图的内容,从而让我们优化顶点和边的索引以进行高效查找。但是,在计算机科学中,有许多开放式问题,在这些问题中,索引不切实际甚至不可能。图遍历让我们可以解决这些问题。遍历让我们可以有效地搜索大型空间,其中对象是通过它们与其他对象的关联关系而不是对象本身的属性来定义的。
从顶点 a 开始,访问其邻居 b,然后访问 b 的邻居 c,并一直进行下去,直到到达“死胡同”,然后迭代回去并访问从倒数第二个访问的顶点可达的节点,并继续应用相同的原则。
// Search in the subgraph for a node matching 'criteria'. Do not re-examine
// nodes listed in 'visited' which have already been tested.
GraphNode depth_first_search(GraphNode node, Predicate criteria, VisitedSet visited) {
// Check that we haven't already visited this part of the graph
if (visited.contains(node)) {
return null;
}
visited.insert(node);
// Test to see if this node satisfies the criteria
if (criteria.apply(node.value)) {
return node;
}
// Search adjacent nodes for a match
for (adjacent in node.adjacentnodes()) {
GraphNode ret = depth_first_search(adjacent, criteria, visited);
if (ret != null) {
return ret;
}
}
// Give up - not in this part of the graph
return null;
}
广度优先搜索访问节点的邻居,然后访问邻居的未访问邻居,等等。如果它从顶点 a 开始,它将访问所有从 a 有边的顶点。如果有些点无法访问,它将不得不从新的顶点开始另一个 BFS。
一个哈希表或哈希映射是一个数据结构,它将键与值相关联。它高效支持的主要操作是查找:给定一个键(例如,一个人的姓名),找到相应的 value(例如,该人的电话号码)。它的工作原理是使用一个哈希函数将键转换为一个哈希,即一个哈希表用来定位所需值的数字。此哈希直接映射到键/值对数组中的一个桶,因此称为哈希映射。映射方法允许我们直接访问任何键/值对的存储位置。
哈希表<元素> 操作
make-hash-table(整数 n):HashTable
- 创建一个包含 n 个桶的哈希表。
get-value(HashTable h, Comparable key):Element
- 返回给定键的元素的值。键必须是某种可比较的类型。
set-value(HashTable h, Comparable key, Element new-value)
- 将给定键的数组元素设置为等于new-value。键必须是某种可比较的类型。
remove(HashTable h, Comparable key)
- 从哈希表中删除给定键的元素。键必须是某种可比较的类型。
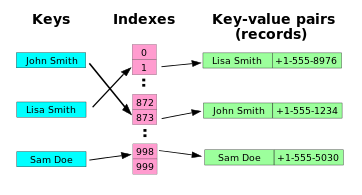
哈希表通常用于实现关联数组、集合和缓存。与数组类似,哈希表提供平均常数时间O(1) 查找,而与表中的项目数量无关。大多数哈希表方案中的(希望很少见的)最坏情况查找时间为 O(n)。[1] 与其他关联数组数据结构相比,当我们需要存储大量数据记录时,哈希表最有用。
哈希表可以用作内存中的数据结构。哈希表也可以用于持久数据结构;数据库索引通常使用基于哈希表的基于磁盘的数据结构。
哈希表还用于在许多数据压缩实现中加快字符串搜索。
一个好的哈希函数对于良好的哈希表性能至关重要。选择一个不好的哈希函数可能会导致聚类行为,其中键映射到同一个哈希桶(即冲突)的概率明显大于随机函数的预期。在任何哈希实现中,冲突的非零概率是不可避免的,但解决冲突的操作数量通常随映射到同一个桶的键的数量线性扩展,因此过多的冲突会显着降低性能。此外,一些哈希函数在计算上很昂贵,因此计算哈希所需的时间(以及在某些情况下,内存)可能很繁重。
选择一个好的哈希函数很棘手。文献中充斥着糟糕的选择,至少在现代标准的衡量下是这样。例如,Knuth 在《计算机程序设计艺术》中倡导的非常流行的乘法哈希(参见下面的参考文献)具有特别糟糕的聚类行为。但是,由于糟糕的哈希只是会降低特定输入键分布的哈希表性能,因此这些问题往往没有被发现。
文献中关于选择哈希函数的标准也很少。与大多数其他基本算法和数据结构不同,关于什么是“好的”哈希函数没有普遍的共识。本节的其余部分按三个标准组织:简单性、速度和强度,并将调查已知按这些标准表现良好的算法。
简单性和速度很容易客观地衡量(例如,通过代码行数和 CPU 基准测试),但强度是一个更难以捉摸的概念。显然,加密哈希函数(如 SHA-1)将满足哈希表所需的相对宽松的强度要求,但它们的速度慢和复杂性使它们不受欢迎。事实上,即使是加密哈希也不能提供保护,以防攻击者想要通过选择全部哈希到同一个桶的键来降低哈希表性能。对于这些特殊情况,应该使用通用哈希函数,而不是任何一个静态哈希,无论它多么复杂。
由于没有标准衡量哈希函数强度的度量方法,目前最先进的方法是使用一系列统计测试来衡量哈希函数是否可以轻易地与随机函数区分开来。可以说,最重要的测试是确定哈希函数是否显示雪崩效应,该效应本质上表明输入密钥的任何单个位变化应该平均影响输出中的一半位。Bret Mulvey 特别主张测试严格雪崩条件,该条件指出,对于任何单个位变化,每个输出位应该以二分之一的概率发生变化,而与密钥中的其他位无关。纯粹的加法哈希函数,例如CRC,在满足这个更强的条件方面表现糟糕。
显然,一个强大的哈希函数应该具有均匀分布的哈希值。Bret Mulvey 建议使用卡方检验来检测均匀性,该检验基于从 21 到 216 的二的幂哈希表大小。该测试比许多其他用于衡量哈希函数的测试敏感得多,并且在许多流行的哈希函数中发现了问题。
幸运的是,有一些好的哈希函数可以满足所有这些标准。最简单的类别都是每次内部循环迭代消耗输入密钥的一个字节。在这个类别中,简单性和速度密切相关,因为快速算法没有时间执行复杂的计算。其中,Jenkins One-at-a-time 哈希表现特别好,它改编自Bob Jenkins 的一篇文章,他是它的创造者。
uint32 joaat_hash(uchar *key, size_t len)
{
uint32 hash = 0;
size_t i;
for (i = 0; i < len; i++)
{
hash += key[i];
hash += (hash << 10);
hash ^= (hash >> 6);
}
hash += (hash << 3);
hash ^= (hash >> 11);
hash += (hash << 15);
return hash;
}

右侧显示了该哈希的雪崩行为。该图像是使用 Bret Mulvey 的 AvalancheTest 在他的Hash.cs 工具集中制作的。每行对应于输入中的单个位,每列对应于输出中的一个位。绿色方块表示良好的混合行为,黄色方块表示弱混合行为,红色表示无混合。最后一个字节中只有几个位是弱混合的,这比许多广泛使用的哈希函数的性能要好得多。
许多常用的哈希函数在经过严格的雪崩测试时表现很差。例如,广受欢迎的FNV 哈希显示了许多位根本没有混合,特别是对于短密钥。查看Bret Mulvey 对 FNV 的评估,以进行更深入的分析。
如果速度比简单性更重要,那么每次迭代消耗多个字节块的哈希函数类别可能令人感兴趣。其中最复杂的一种是 Bob Jenkins 的“lookup3”,它以 12 字节(96 位)块消耗输入。但请注意,使用此哈希带来的任何速度提升,只有在大型密钥上才有可能有用,并且更高的复杂性也可能带来速度问题,例如阻止优化编译器内联哈希函数。Bret Mulvey 分析了早期版本,lookup2,发现它具有出色的雪崩行为。
哈希函数的一个理想属性是,从哈希值(通常为 32 位)到特定大小哈希表的存储桶索引的转换可以通过简单的掩码来完成,只保留较低的 k 位用于大小为 2k 的表(相当于计算哈希值模表大小)。此属性使哈希表大小的增量加倍技术成为可能 - 旧表中的每个存储桶在新表中只映射到两个存储桶。由于其使用 XOR 折叠,FNV 哈希不具有此属性。一些较旧的哈希甚至更糟,要求表大小为素数而不是二的幂,同样将存储桶索引计算为哈希值模表大小。通常,这样的要求是函数基本较弱的迹象;使用素数表大小是使用更强大函数的糟糕替代方案。
冲突解决
[edit | edit source]如果两个密钥映射到同一个索引,则相应的记录不能存储在同一个位置。因此,如果它已经被占用,我们必须找到另一个位置来存储新记录,并且要做到这一点,以便我们以后查找时能够找到它。
为了说明一个好的冲突解决策略的重要性,请考虑以下结果,该结果使用生日悖论推导而来。即使我们假设我们的哈希函数输出随机索引,在均匀分布在数组上,即使对于具有 100 万个条目的数组,在它包含 2500 条记录之前,至少发生一次冲突的概率为 95%。
有很多冲突解决技术,但最流行的是链式和开放寻址。
链式
[edit | edit source]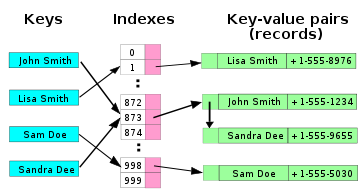
在最简单的链式哈希表技术中,数组中的每个槽位引用一个链表,该链表包含插入到同一个槽位的记录。插入需要找到正确的槽位,并附加到该槽位中的链表的任一端;删除需要搜索链表并进行删除。
链式哈希表相对于开放寻址哈希表具有优势,因为删除操作很简单,并且可以更长时间地推迟表的大小调整,因为即使在每个槽位都被使用的情况下,性能也会更加优雅地降低。事实上,许多链式哈希表可能根本不需要调整大小,因为性能下降是线性的,因为表被填充。例如,包含其推荐容量两倍数据的链式哈希表平均速度大约只是其推荐容量下相同表的两倍。
链式哈希表继承了链表的缺点。在存储小型记录时,链表的开销可能很大。另一个缺点是遍历链表的缓存性能很差。
可以将其他数据结构用于链而不是链表。例如,通过使用自平衡树,哈希表的理论最坏情况时间可以降低到 O(log n) 而不是 O(n)。但是,由于每个链表都旨在很短,因此除非哈希表设计为以最大容量运行,或者存在异常高的碰撞率,否则这种方法通常效率低下,就像在旨在导致碰撞的输入中那样。动态数组也可以用于减少空间开销并在记录很小的情况下提高缓存性能。
一些链式实现使用了一种优化,其中每个链的第一个记录都存储在表中。虽然这可以提高性能,但通常不建议这样做:具有合理负载因子的链式表包含很大比例的空槽位,并且较大的槽位大小会导致它们浪费大量空间。
开放寻址
[edit | edit source]
开放寻址哈希表可以将记录直接存储在数组中。哈希冲突通过探测来解决,或者搜索数组中的备选位置(探测序列),直到找到目标记录,或者找到一个未使用的数组槽位,这表明表中不存在这样的键。众所周知的探测序列包括
- 线性探测
- 其中探测之间的间隔是固定的——通常为 1,
- 二次探测
- 其中探测之间的间隔线性增加(因此,索引由二次函数描述),以及
- 双重哈希
- 其中探测之间的间隔对于每个记录都是固定的,但由另一个哈希函数计算。
这些方法之间的主要权衡是,线性探测具有最佳的缓存性能,但对聚集最敏感,而双散列具有较差的缓存性能,但几乎没有聚集;二次散列在这两个方面都处于中间位置。双散列也可能比其他探测形式需要更多的计算。一些开放地址方法,例如后进先出散列和布谷鸟散列在数组中移动现有键以腾出空间以容纳新键。与基于探测的方法相比,这提供了更好的最大搜索时间。
对开放地址哈希表性能的关键影响是负载因子;也就是说,数组中使用的槽位的比例。当负载因子增加到 100% 时,查找或插入给定键所需的探测次数会急剧增加。一旦表已满,探测算法甚至可能无法终止。即使使用良好的散列函数,负载因子通常也限制在 80%。一个不好的散列函数即使在非常低的负载因子下也能表现出较差的性能,因为它会产生大量的聚集。导致散列函数聚集的原因尚不清楚,并且很容易无意中编写会导致严重聚集的散列函数。
示例伪代码
[edit | edit source]以下伪代码是开放地址哈希表使用线性探测和单槽步进的实现,这是一种常见的有效方法,如果散列函数很好。查找、设置和删除函数中的每一个都使用一个通用的内部函数findSlot来定位数组槽,该槽要么包含给定键,要么应该包含给定键。
record pair { key, value }
var pair array slot[0..numSlots-1]
function findSlot(key)
i := hash(key) modulus numSlots
loop
if slot[i] is not occupied or slot[i].key = key
return i
i := (i + 1) modulus numSlots
function lookup(key)
i := findSlot(key)
if slot[i] is occupied // key is in table
return slot[i].value
else // key is not in table
return not found
function set(key, value)
i := findSlot(key)
if slot[i].key = key
// (Key already in table. Update value.)
slot[i].value := value
else
// (Insert key and value in un-occupied slot.)
// (But first, make sure insert won't overload the table)
if the table is almost full
rebuild the table larger (note 1)
i := findSlot(key)
slot[i].key := key
slot[i].value := value
另一个展示开放地址技术的示例。所呈现的函数将互联网协议地址的每个部分(4)进行转换,其中 NOT 是按位取反,XOR 是按位异或,OR 是按位或,AND 是按位与,<< 和 >> 是左移和右移。
// key_1,key_2,key_3,key_4 are following 3-digit numbers - parts of ip address xxx.xxx.xxx.xxx
function ip(key parts)
j := 1
do
key := (key_2 << 2)
key := (key + (key_3 << 7))
key := key + (j OR key_4 >> 2) * (key_4) * (j + key_1) XOR j
key := key AND _prime_ // _prime_ is a prime number
j := (j+1)
while collision
return key
- 注释 1
- 重建表需要分配一个更大的数组,并递归使用设置操作将旧数组的所有元素插入到新的更大数组中。通常以指数方式增加数组大小,例如将旧数组大小加倍。
function remove(key)
i := findSlot(key)
if slot[i] is unoccupied
return // key is not in the table
j := i
loop
j := (j+1) modulus numSlots
if slot[j] is unoccupied
exit loop
k := hash(slot[j].key) modulus numSlots
if (j > i and (k <= i or k > j)) or
(j < i and (k <= i and k > j)) (note 2)
slot[i] := slot[j]
i := j
mark slot[i] as unoccupied
- 注释 2
- 对于集群中的所有记录,其自然散列位置与其当前位置之间不得有空闲槽(否则查找将在找到记录之前终止)。在伪代码中的这一点上,i 是一个空闲槽,它可能会使集群中后续记录的此属性失效。j 是这样的后续记录。k 是记录在j 处自然落在哈希表中的原始散列,如果不存在冲突。此测试是在询问记录j 是否相对于集群的必要属性被无效地定位,现在i 是空闲的。
另一种删除技术是简单地将槽标记为已删除。但是,最终需要重建表才能简单地删除已删除的记录。以上方法提供了对现有记录的 O(1) 更新和删除,如果表的最高水位标记增加,则偶尔会重建。
上面的 O(1) 删除方法只适用于线性探测的哈希表,具有单槽步进。在一次操作中需要删除许多记录的情况下,标记要删除的槽位并稍后重建可能更高效。
开放地址与链式
[edit | edit source]与开放地址相比,链式哈希表具有以下优点
- 它们易于有效地实现,并且只需要基本数据结构。
- 从编写合适的散列函数的角度来看,链式哈希表对聚集不敏感,只需要最小化冲突。开放地址依赖于更好的散列函数来避免聚集。如果新手程序员可以添加自己的散列函数,这一点尤其重要,但即使是经验丰富的程序员也会被意想不到的聚集效应所困扰。
- 它们的性能下降更加平稳。虽然链随着表的填充而变长,但链式哈希表不会“填满”,也不会表现出在接近满的表中使用开放地址时出现的查找时间突然增加。(参见右侧)
- 如果哈希表存储大型记录,每个记录约 5 个或更多个字,则链式比开放地址使用更少的内存。
- 如果哈希表是稀疏的(即它有一个大型数组,其中有很多空数组槽),则即使对于每个记录只有 2 到 4 个字的小型记录,链式也比开放地址使用更少的内存,因为它的外部存储。

对于小型记录大小(几个字或更少),与链式相比,就地开放地址的优势在于
- 它们可能比链式更节省空间,因为它们不需要存储任何指针或在哈希表之外分配任何额外的空间。简单的链表每个元素需要一个字的开销。
- 插入避免了内存分配的时间开销,甚至可以在没有内存分配器的情况下实现。
- 由于它使用内部存储,因此开放地址避免了链式外部存储所需的额外间接寻址。它还具有更好的局部性,尤其是对于线性探测。对于小型记录大小,这些因素可以产生比链式更好的性能,尤其是对于查找。
- 它们更容易序列化,因为它们不使用指针。
另一方面,对于大型元素,普通开放地址是一个糟糕的选择,因为这些元素会填充整个缓存行(抵消缓存优势),并且在大型空表槽位上会浪费大量空间。如果开放地址表只存储对元素的引用(外部存储),那么即使对于大型记录,它也使用与链式相当的空间,但会失去其速度优势。
一般来说,开放地址更适合用于具有小型记录的哈希表,这些记录可以存储在表中(内部存储)并适合缓存行。它们特别适合一个字或更少的元素。在预计表将具有高负载因子、记录很大或数据大小可变的情况下,链式哈希表通常可以执行得一样好或更好。
最终,明智地使用任何类型的哈希表算法通常都足够快;并且在哈希表代码中花费的计算百分比很低。内存使用量很少被认为过大。因此,在大多数情况下,这些算法之间的差异是微不足道的,并且其他考虑因素通常会起作用。
合并散列
[edit | edit source]合并散列是链式和开放地址的混合体,它在表本身内将节点链链接在一起。与开放地址一样,它实现了比链式更高的空间使用率和(略微降低的)缓存优势。与链式一样,它不会表现出聚集效应;事实上,表可以有效地填充到很高的密度。与链式不同,它不能拥有比表槽更多的元素。
完美散列
[edit | edit source]如果所有将要使用的键都已提前知道,并且没有更多键可以适合哈希表,则可以使用完美散列来创建一个完美散列表,其中不会发生冲突。如果使用最小完美散列,哈希表中的每个位置也可以使用。
完美散列提供了一个哈希表,其中查找时间在最坏情况下是恒定的。这与链式和开放地址方法形成对比,在这些方法中,查找时间平均较低,但可能会任意大。存在用于在插入键时维护完美散列函数的方法,称为动态完美散列。一个更简单的替代方案,它也提供最坏情况下的恒定查找时间,是布谷鸟散列.
解决冲突的最简单方法可能是用新值替换已存在于槽中的值,或者不太常见的是,丢弃要插入的记录。在后面的搜索中,这可能会导致搜索找不到已插入的记录。此技术对于实现缓存特别有用。
一个更节省空间的解决方案类似于此,它使用 位数组(一个一位字段数组)作为我们的表格。最初所有位都被设置为零,当我们插入一个键时,我们将相应的位设置为一。不会发生假阴性,但可能会发生 假阳性,因为如果搜索找到一个 1 位,它会声称找到了该值,即使它只是一个巧合地哈希到同一数组槽中的另一个值。实际上,这样的哈希表仅仅是一种特定的 布隆过滤器。
使用良好的哈希函数,哈希表通常可以包含大约 70%–80% 的表格槽位数量的元素,并且仍然能够很好地执行。根据冲突解决机制的不同,随着添加更多元素,性能可能会逐渐或大幅度下降。为了解决这个问题,当负载因子超过某个阈值时,我们会分配一个新的、更大的表,并将原始表中的所有内容添加到这个新表中。例如,在 Java 的 HashMap 类中,默认的负载因子阈值为 0.75。
这可能是一个非常昂贵的操作,它的必要性是哈希表的一个缺点。事实上,一些简单的实现方法,例如在每次添加新元素时将表扩大一个,会大大降低性能,以至于使哈希表变得毫无用处。但是,如果我们以固定的百分比(例如 10% 或 100%)扩大表,则可以使用 摊销分析 来证明这些调整大小的频率很低,以至于每次查找的平均时间仍然是常数时间。为了了解为什么这是真的,假设一个使用链式哈希表的哈希表从最小大小 1 开始,并在每次填充满超过 100% 时加倍。如果最后它包含了 n 个元素,那么为所有调整大小执行的总添加操作次数为
- 1 + 2 + 4 + ... + n = 2n - 1。
因为调整大小的成本构成一个 几何级数,所以总成本为 O(n)。但是,我们还执行了 n 个操作来添加最初的 n 个元素,所以添加 n 个元素并调整大小的总时间为 O(n),每个元素的摊销时间为 O(1)。
另一方面,一些哈希表实现,特别是在 实时系统 中,无法承受一次性扩大哈希表的代价,因为它可能会中断时间关键的操作。一种简单的方法是最初为预期的元素数量分配足够的内存,并禁止添加过多的元素。另一种有用的但更占内存的技术是逐步执行调整大小
- 分配新的哈希表,但保留旧的哈希表,并在查找时检查这两个表。
- 每次执行插入操作时,将该元素添加到新表中,并将 k 个元素从旧表移动到新表中。
- 当所有元素都从旧表中移除时,释放旧表。
为了确保在新的表本身需要扩大之前完全复制旧表,在调整大小期间必须将表的大小至少增加 (k + 1)/k 倍。
线性哈希 是一种允许增量哈希表扩展的哈希表算法。它是使用一个单一的哈希表实现的,但是有两个可能的查找函数。
另一种降低表调整大小成本的方法是选择一种哈希函数,这样大多数值的哈希值在表调整大小后不会改变。这种方法称为 一致性哈希,在基于磁盘和分布式哈希中很普遍,因为调整大小成本过高。
哈希表以伪随机位置存储数据,因此以排序方式访问数据是一个非常耗时的操作。其他数据结构,如 自平衡二叉搜索树 通常操作速度更慢(因为它们的查找时间为 O(log n)),并且实现起来比哈希表复杂得多,但始终保持排序的数据结构。参见 哈希表和自平衡二叉搜索树的比较。
虽然哈希表查找平均使用常数时间,但花费的时间可能很长。评估一个好的哈希函数可能是一个缓慢的操作。特别是,如果可以使用简单的数组索引代替,这通常更快。
哈希表通常表现出较差的 局部性——也就是说,要访问的数据似乎随机分布在内存中。由于哈希表导致跳跃的访问模式,这会导致 微处理器缓存 未命中,从而导致长时间延迟。紧凑的数据结构(如使用 线性搜索 搜索的数组)可能更快,如果表相对较小,并且密钥比较起来很便宜,例如使用简单的整数密钥。根据 摩尔定律,缓存大小呈指数级增长,因此被认为“小”的范围可能正在扩大。最佳性能点因系统而异;例如,在 Parrot 上的测试表明,它的哈希表在除最简单情况(一到三个条目)以外的所有情况下都优于线性搜索。
更重要的是,哈希表更难编写和使用,并且更容易出错。哈希表要求为每种密钥类型设计一个有效的哈希函数,在许多情况下,这比自平衡二叉搜索树所需的设计和调试比较函数更困难、更费时。在开放地址哈希表中,创建糟糕的哈希函数更容易。
此外,在某些应用程序中,具有哈希函数知识的 黑客 能够向哈希提供信息,从而通过导致过多的冲突来创建最坏情况的行为,从而导致非常糟糕的性能(即 拒绝服务攻击)。在关键应用程序中,可以使用 通用哈希 或者可能更喜欢具有更好最坏情况保证的数据结构。有关详细信息,请参见 Crosby 和 Wallach 的文章 Denial of Service via Algorithmic Complexity Attacks。
可扩展哈希 和 线性哈希 是哈希算法,用于数据库算法中,例如索引文件结构,甚至数据库的主文件组织。通常,为了使大型数据库的搜索可扩展,搜索时间应该与 log N 或接近常数成正比,其中 N 是要搜索的记录数。log N 搜索可以通过树结构实现,因为扇出度和树的高度与找到记录所需的步骤数相关,所以树的高度是找到记录所需的最大磁盘访问次数。然而,哈希表也被使用,因为磁盘访问的成本可以用磁盘访问的单位来计算,并且该单位通常是数据块。由于哈希表在最佳情况下可以使用一次或两次访问找到键,所以哈希表索引在检索连接操作期间的记录集合时通常被认为更快,例如。
SELECT * from customer, orders where customer.cust_id = orders.cust_id and cust_id = X
例如,如果 orders 有一个关于 cust_id 的哈希索引,那么定位包含与 cust_id = X 匹配的订单记录位置的块将花费常数时间。(虽然,如果 orders 的值类型是订单 ID 列表,那么哈希键将只是每个订单批次的一个唯一的 cust_id,这将避免不必要的冲突)。
可扩展哈希和线性哈希有一些相似之处:冲突被认为是不可避免的,并且是算法的一部分,其中添加了冲突空间的块或桶;需要传统的良好哈希函数范围,但哈希值通过动态地址函数进行转换;在 可扩展哈希 中,使用位掩码来屏蔽不需要的位,但该掩码长度会周期性地增加一,使可用寻址空间翻倍;在可扩展哈希中,还有一个间接寻址目录地址空间,目录条目与另一个地址(指针)配对,指向包含键值对的实际块;目录中的条目对应于位掩码后的哈希值(因此条目数量等于最大位掩码值 + 1,例如 2 位位掩码,可以寻址一个包含 00 01 10 11 的目录,或 3 + 1 = 4)。
在 线性哈希 中,传统的哈希值也使用位掩码进行掩码,但如果得到的较小哈希值低于“分裂”变量,则原始哈希值使用比它长一位的位掩码进行掩码,使得到的哈希值寻址最近添加的块。分裂变量在 0 到当前最大位掩码值之间递增,例如 2 位位掩码,或在线性哈希术语中,级别为 2,分裂变量将在 0 到 3 之间变化。当分裂变量达到 4 时,级别增加 1,所以在下一轮分裂变量中,它将在 0 到 7 之间变化,并在达到 8 时重置。
分裂变量递增允许增加寻址空间,因为新块被添加;每次插入键值对并且溢出键值对键所映射到的特定块时,就会决定添加一个新块。这个溢出位置可能与分裂变量所指向的要分裂的块完全无关。但是,随着时间的推移,如果假设给定一个良好的随机哈希函数,它将条目均匀地分布在所有可寻址块中,那么实际上需要分裂的块(因为它们溢出了)将会按照循环的方式依次获得机会,因为分裂值在 0 到 N 之间变化,其中 N 是 2 的 level 次方的倍数,level 是分裂变量达到 N 时递增的变量。
使用可扩展哈希和线性哈希都一次添加一个新块。
在 可扩展哈希 中,块溢出(一个新的键值与 B 个其他键值冲突,其中 B 是一个块的大小)通过检查位掩码的大小“本地”处理,称为“局部深度”,这是一个必须与块一起存储的属性。目录结构也具有深度,称为“全局深度”。如果局部深度小于全局深度,那么局部深度就会增加,并且所有键值都会重新哈希并通过现在长一位的位掩码,将它们放置在当前块或另一个块中。如果另一个块在目录中查找时碰巧是同一个块,那么就会添加一个新块,并且另一个块的目录条目将指向新块。为什么目录中有两个条目指向同一个块?这是因为如果局部深度等于目录的全局深度,这意味着目录的位掩码没有足够的位来处理块位掩码长度的递增,因此目录必须递增其位掩码长度,但这意味着目录现在将可寻址条目数量翻倍。由于一半的可寻址条目不存在,目录只是将指针复制到新的条目中,例如,如果目录包含 00、01、10、11 的条目,或 2 位位掩码,并且它变成了 3 位位掩码,那么 000 001 010 011 100 101 110 111 将成为新的条目,并且 00 的块地址将指向 000 和 001;01 的指针指向 010 和 011,10 指向 100 和 101,等等。因此,这种情况导致了两个目录条目指向同一个块。虽然即将溢出的块现在可以通过将第二个指针重定向到新添加的块来添加一个新块,但其他原始块将有两个指向它们的指针。当它们轮到分裂时,算法将检查局部深度和全局深度,这一次会发现局部深度更小,因此不需要目录分裂,只需要添加一个新块,并将第二个目录指针从指向以前的块移动到指向新块。
在 线性哈希 中,添加一个类似哈希的块不会在块溢出时立即发生,因此会创建一个溢出块来附加到溢出块。然而,块溢出表明需要更多空间,这是通过分裂“分裂”变量所指向的块实现的,该变量最初为零,因此最初指向块零。分裂是通过获取分裂块中所有键值对及其溢出块(如果有),再次哈希键,但使用长度为当前级别 + 1 的位掩码来完成的。这将导致两个块地址,一些将是旧的块号,而另一些将是
a2 = old block number + ( N times 2 ^ (level) )
- 基本原理
令 m = N 乘以 2 的 level 次方;如果 h 是原始哈希值,并且旧块号 = h mod m,现在新的块号是 h mod ( m * 2 ),因为 m * 2 = N 乘以 2 的 (level+1) 次方,那么新的块号是 h mod m 如果 (h / m) 是偶数,所以将 h/m 除以 2 会留下一个零余数,因此不会改变余数,或者新的块号是 ( h mod m ) + m,因为 h / m 是一个奇数,将 h / m 除以 2 会留下 m 的剩余余数,加上原始余数。(相同的原理适用于可扩展哈希深度递增)。
如上所述,使用编号为 a2 的新块创建,这通常发生在 +1 的先前 a2 值上。完成此操作后,分裂变量就会递增,以便下一个 a2 值将再次是旧的 a2 + 1。通过这种方式,每个块最终都会被分裂变量覆盖,因此每个块都会被预先重新哈希到额外的空间中,并且新块会被逐步添加。不再需要的溢出块会被丢弃,以便在需要时进行垃圾收集,或者通过链接放到一个可用的空闲块列表中。
当分裂变量达到 ( N 乘以 2 的 level 次方 ) 时,level 就会递增,分裂变量就会重置为零。在下一轮中,分裂变量现在将从零遍历到 ( N 乘以 2 的 (old_level + 1) 次方 ),这与上一轮开始时的块数完全相同,但包括上一轮创建的所有块。
对线性哈希和可扩展哈希的文件存储映射的简单推论
[edit | edit source]可以看出,可扩展哈希需要空间来存储一个目录,该目录可以翻倍。
由于两种算法的空间都是一次增加一个块,如果块具有已知的最大尺寸或固定尺寸,那么将块映射为顺序附加到文件的块是直接的。
在可扩展哈希中,将目录存储为一个单独的文件是有逻辑的,因为翻倍可以通过将文件附加到目录文件的末尾来实现。单独的块文件不需要改变,除了将块附加到它的末尾。
线性哈希的标题信息不会增加大小:基本上只需要记录 N、level 和 split 的值,因此可以将这些值作为标题合并到固定块大小的线性哈希存储文件中。
然而,线性哈希需要空间来存放溢出块,这最好存储在另一个文件中,否则在线性哈希文件中寻址块并不像将块号乘以块大小然后加上 N、level 和 split 的空间那样简单。
在下一节中,给出了用 Java 实现的线性哈希的完整示例,使用内存中实现的线性哈希,以及代码来管理文件目录中的文件块,文件目录的整个内容代表持久线性哈希结构。
实现
[edit | edit source]虽然许多编程语言已经提供了哈希表功能,[2] 但有一些独立的实现值得一提。
- Google Sparse Hash Google SparseHash 项目包含几个 Google 使用的哈希映射实现,具有不同的性能特征,包括一个针对空间进行优化的实现和一个针对速度进行优化的实现。内存优化的实现非常节省内存,只有 2 位/条目的开销。
- MCT 提供类似于 Google 的
dense_hash_map的哈希表,但对包含的值没有限制;它还提供异常安全性并支持 C++0x 功能。 - 许多运行时语言和/或标准库使用哈希表来实现它们对关联数组的支持,因为它们的效率很高。
可扩展哈希的 Python 实现
[edit | edit source]文件 - 块管理例程不存在,因此可以添加进来,使之成为数据库哈希索引的真实实现。
一个完整页面根据(本地深度)th 位进行分割,首先收集指向完整页面的所有目录索引,根据 d 位为 0 或 1(分别对应第一和第二新页面)更新指针,然后在对每个键进行哈希并使用每个哈希的 d 位来查看要分配到哪个页面之后,重新加载所有键值对。每个新页面的本地深度比旧页面的本地深度大 1,这样在下一次分割时可以使用下一个 d 位。
PAGE_SZ = 20
class Page:
def __init__(self):
self.m = {}
self.d = 0
def full(self):
return len(self.m) > PAGE_SZ
def put(self,k,v):
self.m[k] = v
def get(self,k):
return self.m.get(k)
class EH:
def __init__(self):
self.gd = 0
p = Page()
self.pp= [p]
def get_page(self,k):
h = hash(k)
p = self.pp[ h & (( 1 << self.gd) -1)]
return p
def put(self, k, v):
p = self.get_page(k)
if p.full() and p.d == self.gd:
self.pp = self.pp + self.pp
self.gd += 1
if p.full() and p.d < self.gd:
p.put(k,v);
p1 = Page()
p2 = Page()
for k2 in p.m.keys():
v2 = p.m[k2]
h = k2.__hash__()
h = h & ((1 << self.gd) -1)
if (h | (1 << p.d) == h):
p2.put(k2,v2)
else:
p1.put(k2,v2)
l = []
for i in xrange(0, len(self.pp)):
if self.pp[i] == p:
l.append(i)
for i in l:
if (i | ( 1 << p.d) == i):
self.pp[i] = p2
else:
self.pp[i] = p1
p1.d = p.d + 1
p2.d = p1.d
else:
p.put(k, v)
def get(self, k):
p = self.get_page(k)
return p.get(k)
if __name__ == "__main__":
eh = EH()
N = 10000
l = []
for i in range(0,N):
l.append(i)
import random
random.shuffle(l)
for i in l:
eh.put(i,i)
print l
for i in range(0, N):
print eh.get(i)
可扩展哈希的 Java 实现
[edit | edit source]上面 Python 代码的直接 Java 翻译,经测试可以使用。
package ext_hashing;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Map;
import java.util.Random;
public class EH2<K, V> {
static class Page<K, V> {
static int PAGE_SZ = 20;
private Map<K, V> m = new HashMap<K, V>();
int d = 0;
boolean full() {
return m.size() > PAGE_SZ;
}
void put(K k, V v) {
m.put(k, v);
}
V get(K k) {
return m.get(k);
}
}
int gd = 0;
List<Page<K, V>> pp = new ArrayList<Page<K, V>>();
public EH2() {
pp.add(new Page<K, V>());
}
Page<K, V> getPage(K k) {
int h = k.hashCode();
Page<K, V> p = pp.get(h & ((1 << gd) - 1));
return p;
}
void put(K k, V v) {
Page<K, V> p = getPage(k);
if (p.full() && p.d == gd) {
List<Page<K, V>> pp2 = new ArrayList<EH2.Page<K, V>>(pp);
pp.addAll(pp2);
++gd;
}
if (p.full() && p.d < gd) {
p.put(k, v);
Page<K, V> p1, p2;
p1 = new Page<K, V>();
p2 = new Page<K, V>();
for (K k2 : p.m.keySet()) {
V v2 = p.m.get(k2);
int h = k2.hashCode() & ((1 << gd) - 1);
if ((h | (1 << p.d)) == h)
p2.put(k2, v2);
else
p1.put(k2, v2);
}
List<Integer> l = new ArrayList<Integer>();
for (int i = 0; i < pp.size(); ++i)
if (pp.get(i) == p)
l.add(i);
for (int i : l)
if ((i | (1 << p.d)) == i)
pp.set(i, p2);
else
pp.set(i, p1);
p1.d = p.d + 1;
p2.d = p1.d;
} else
p.put(k, v);
}
public V get(K k) {
return getPage(k).get(k);
}
public static void main(String[] args) {
int N = 500000;
Random r = new Random();
List<Integer> l = new ArrayList<Integer>();
for (int i = 0; i < N; ++i) {
l.add(i);
}
for (int i = 0; i < N; ++i) {
int j = r.nextInt(N);
int t = l.get(j);
l.set(j, l.get(i));
l.set(i, t);
}
EH2<Integer, Integer> eh = new EH2<Integer, Integer>();
for (int i = 0; i < N; ++i) {
eh.put(l.get(i), l.get(i));
}
for (int i = 0; i < N; ++i) {
System.out.printf("%d:%d , ", i, eh.get(i));
if (i % 10 == 0)
System.out.println();
}
}
}
线性哈希的 Java 实现
[edit | edit source](可用于任意大小的简单数据库索引,(几乎?))
这段代码源于对更大 Java HashMap 的需求。最初,Java HashMap 标准对象用作 Map 来索引类似堆的数据库文件(DBF 格式)。但是后来,遇到了一个包含太多记录的文件,导致抛出 OutOfMemoryError,因此线性哈希似乎是一个相当简单的算法,可以用作基于磁盘的索引方案。
最初,线性哈希是在 Java Map 接口之后实现的,主要是 put(k,v) 和 get(k,v) 方法。使用了泛型,为了不陷入键值对的细节。
调试以实现功能
[edit | edit source]自定义转储到 System.err 用于验证块是否已创建、填充,以及溢出块的数量是否符合预期(数量 = 1)。所有这些都是在纯内存实现中完成的。
后来,引入了标准的 Java 解耦,原始的 LHMap2 类接受事件的侦听器,例如需要块时。然后将侦听器实现为块文件管理器,每当在块列表上遇到空块时,将块加载到内存 LHMap2 对象的块列表中,并检查虚拟机运行时空闲内存是否不足,并使用最基本的先到先出缓存删除算法(不是最近使用 (LRU),也不是最少使用)通过将它们保存到磁盘文件,然后主动调用系统垃圾收集器来退休块。
由于存在应用程序用例,即外部索引大型 DBF 表,因此该用例被用作算法实现的主要测试工具。
package linearhashmap;
import java.io.Externalizable;
import java.io.IOException;
import java.io.ObjectInput;
import java.io.ObjectOutput;
import java.io.Serializable;
import java.util.ArrayList;
import java.util.Collection;
import java.util.Iterator;
import java.util.LinkedList;
import java.util.List;
import java.util.Map;
import java.util.Set;
import java.util.TreeMap;
import java.util.TreeSet;
/**
*
* @param <K>
* key type , must implement equals() and hashCode()
* @param <V>
* value type
*
*
*/
public class LHMap2<K, V> implements Map<K, V>, Serializable {
/**
*
*/
private static final long serialVersionUID = 3095071852466632996L;
/**
*
*/
public static interface BlockListener<K, V> {
public void blockRequested(int block, LHMap2<K, V> map);
}
List<BlockListener<K, V>> listeners = new ArrayList<BlockListener<K, V>>();
// int savedBlocks;
int N;
int level = 0;
int split = 0;
int blockSize;
long totalWrites = 0;
List<Block<K, V>> blockList = new ArrayList<Block<K, V>>();
public void addBlockListener(BlockListener<K, V> listener) {
listeners.add(listener);
}
void notifyBlockRequested(int block) {
for (BlockListener<K, V> l : listeners) {
l.blockRequested(block, this);
}
}
public LHMap2(int blockSize, int nStartingBlocks) {
this.blockSize = blockSize;
this.N = nStartingBlocks;
for (int i = 0; i < nStartingBlocks; ++i) {
addBlock();
}
Runtime.getRuntime().addShutdownHook(new Thread(new Runnable() {
@Override
public void run() {
showStructure();
}
}));
}
public static class Block<K, V> implements Externalizable {
/**
*
*/
int j = 0;
Block<K, V> overflow = null;
LinkedList<K> keyList = new LinkedList<K>();
LinkedList<V> valueList = new LinkedList<V>();
transient private LHMap2<K, V> owner;
transient private Map<K, V> shadow = new TreeMap<K, V>();
private boolean changed = false;
private int size = 0;
public LHMap2<K, V> getOwner() {
return owner;
}
public void setOwner(LHMap2<K, V> owner) {
this.owner = owner;
Block<K, V> ov = overflow;
while (ov != null) {
overflow.setOwner(owner);
ov = ov.overflow;
}
}
public Block() {
super();
}
public Block(LHMap2<K, V> map) {
setOwner(map);
}
public V put(K k, V v) {
setChanged(true);
V v2 = replace(k, v);
if (v2 == null) {
++size;
if (keyList.size() == getOwner().blockSize) {
if (overflow == null) {
getOwner().blockOverflowed(this, k, v);
} else {
overflow.put(k, v);
}
} else {
keyList.addFirst(k);
valueList.addFirst(v);
}
}
return v2;
}
void setChanged(boolean b) {
changed = b;
}
public Map<K, V> drainToMap(Map<K, V> map) {
while (!keyList.isEmpty()) {
K k = keyList.removeLast();
V v = valueList.removeLast();
map.put(k, v);
}
if (overflow != null)
map = overflow.drainToMap(map);
garbageCollectionOverflow();
return map;
}
public void updateMap(Map<K, V> map) {
Iterator<K> ik = keyList.descendingIterator();
Iterator<V> iv = valueList.descendingIterator();
while (ik.hasNext() && iv.hasNext()) {
map.put(ik.next(), iv.next());
}
if (overflow != null)
overflow.updateMap(map);
}
private void garbageCollectionOverflow() {
if (overflow != null) {
overflow.garbageCollectionOverflow();
overflow = null;
}
}
public void addOverflowBucket() {
// assert overflow is needed
if (keyList.size() < getOwner().blockSize)
return;
if (overflow == null) {
overflow = new Block<K, V>(getOwner());
} else {
overflow.addOverflowBucket();
}
}
public V replace(K key, V v2) {
if (overflow != null) {
V v = overflow.replace(key, v2);
if (v != null)
return v;
}
Iterator<K> i = keyList.listIterator();
int j = 0;
while (i.hasNext()) {
if (key.equals(i.next())) {
V v = valueList.get(j);
if (v2 != null) {
valueList.set(j, v2);
}
return v;
}
++j;
}
return null;
}
public boolean isChanged() {
return changed;
}
@Override
public void readExternal(ObjectInput arg0) throws IOException,
ClassNotFoundException {
int sz = arg0.readInt();
for (int i = 0; i < sz; ++i) {
K k = (K) arg0.readObject();
V v = (V) arg0.readObject();
shadow.put(k, v);
}
}
public void loadFromShadow(LHMap2<K, V> owner) {
setOwner(owner);
Block<K, V> b = this;
for (K k : shadow.keySet()) {
if (b.keyList.size() == owner.blockSize) {
Block<K, V> overflow = new Block<K, V>(owner);
b.overflow = overflow;
b = overflow;
}
b.keyList.add(k);
b.valueList.add(shadow.get(k));
}
shadow.clear();
}
@Override
public void writeExternal(ObjectOutput arg0) throws IOException {
if (!changed)
return;
Map<K, V> map = new TreeMap<K, V>();
updateMap(map);
int sz = map.size();
arg0.writeInt(sz);
for (K k : map.keySet()) {
arg0.writeObject(k);
arg0.writeObject(map.get(k));
}
setChanged(false);
}
}
void init() {
for (int i = 0; i < N; ++i) {
addBlock();
}
}
/**
* @param hashValue
* @return a bucket number.
*/
int getDynamicHash(int hashValue) {
long unsignedHash = ((long) hashValue << 32) >>> 32;
// ^^ this long cast needed
int h = (int) (unsignedHash % (N << level));
// System.err.println("h = " + h);
if (h < split) {
h = (int) (unsignedHash % (N << (level + 1)));
// System.err.println("h < split, new h = " + h);
}
return h;
}
@Override
public V put(K k, V v) {
++totalWrites;
int h = getDynamicHash(k.hashCode());
Block<K, V> b = getBlock(h);
b.put(k, v);
return v;
}
public long getTotalWrites() {
return totalWrites;
}
private Block<K, V> getBlock(int h) {
notifyBlockRequested(h);
return blockList.get(h);
}
void blockOverflowed(Block<K, V> b, K k, V v) {
splitNextBucket();
b.addOverflowBucket();
b.put(k, v);
}
private void splitNextBucket() {
Block<K, V> b = getBlock(split);
TreeMap<K, V> map = new TreeMap<K, V>();
b.drainToMap(map);
addBlock();
System.err.printf("split N LEVEL %d %d %d \n", split, N, level);
if (++split >= (N << level)) {
++level;
split = 0;
}
for (K k : map.keySet()) {
V v = map.get(k);
int h = getDynamicHash(k.hashCode());
System.err.println(h + " ");
Block<K, V> b2 = getBlock(h);
b2.put(k, v);
}
}
private Block<K, V> addBlock() {
Block<K, V> b = new Block<K, V>(this);
blockList.add(b);
return b;
}
@Override
public void clear() {
blockList = new ArrayList<Block<K, V>>();
split = 0;
level = 0;
totalWrites = 0;// savedBlocks = 0;
}
@Override
public boolean containsKey(Object key) {
return get(key) != null;
}
@Override
public boolean containsValue(Object value) {
return values().contains(value);
}
@Override
public Set<java.util.Map.Entry<K, V>> entrySet() {
TreeSet<Map.Entry<K, V>> set = new TreeSet<Map.Entry<K, V>>();
Set<K> kk = keySet();
for (K k : kk) {
final K k2 = k;
set.add(new Entry<K, V>() {
@Override
public K getKey() {
return k2;
}
@Override
public V getValue() {
return get(k2);
}
@Override
public V setValue(V value) {
return put(k2, value);
}
});
}
return set;
}
@Override
public V get(Object key) {
int h = getDynamicHash(key.hashCode());
Block<K, V> b = getBlock(h);
return b.replace((K) key, null);
}
@Override
public boolean isEmpty() {
return size() == 0;
}
@Override
public Set<K> keySet() {
TreeSet<K> kk = new TreeSet<K>();
for (int i = 0; i < blockList.size(); ++i) {
Block<K, V> b = getBlock(i);
kk.addAll(b.keyList);
Block<K, V> ov = b.overflow;
while (ov != null) {
kk.addAll(ov.keyList);
ov = ov.overflow;
}
}
return kk;
}
@Override
public void putAll(Map<? extends K, ? extends V> m) {
for (K k : m.keySet()) {
put(k, m.get(k));
}
}
@Override
public V remove(Object key) {
return null;
}
@Override
public int size() {
long sz = longSize();
return (int) (sz > Integer.MAX_VALUE ? Integer.MAX_VALUE
: sz);
}
public long longSize() {
long sz = 0;
for (Block<K, V> b : blockList) {
Block<K, V> b1 = b;
while (b1 != null) {
sz += b1.size;
b1 = b.overflow;
}
}
return sz;
}
@Override
public Collection<V> values() {
ArrayList<V> list = new ArrayList<V>();
Set<K> kk = keySet();
for (K k : kk) {
list.add(get(k));
}
return list;
}
private void showStructure() {
for (int i = 0; i < blockList.size(); ++i) {
Block<K, V> b = getBlock(i);
Block<K, V> ov = b.overflow;
int k = 0;
while (ov != null) {
ov = ov.overflow;
++k;
}
System.out.println("Block " + i + " size " + b.keyList.size()
+ " overflow blocks = " + k);
}
}
}
在这个实现中,每个块都是一个文件,因为块在这里是可变大小的,以考虑泛型和可变大小的键值对,溢出块是概念性的,而不是实际的磁盘存储,因为块的内容及其溢出桶(如果存在)的内容,在这个实现中,以交替的键值对列表的形式保存。使用标准的 Java 自定义对象持久化方式,在 Block 数据类中实现 Externalizable 接口,方法用于保存和加载到 Object 流。
package linearhashmap;
import java.io.ByteArrayInputStream;
import java.io.ByteArrayOutputStream;
import java.io.File;
import java.io.FileInputStream;
import java.io.FileNotFoundException;
import java.io.FileOutputStream;
import java.io.IOException;
import java.io.ObjectInputStream;
import java.io.ObjectOutputStream;
import java.io.Serializable;
import java.util.ArrayList;
import java.util.Random;
/**
* This class manages the LHMap2 class block disk swapping, and saves and load an instance of the LHMap2 class.
* It has been used to externally index a legacy file based database of 100,000 record master table, and 1,000,000 record
* sized child tables, and accounts for heap space available in the java virtual machine, so that OutOfMemory errors
* are avoided when the heap space is low by putting blocks back on files, and garbage collecting them.
* The main performance bottleneck appeared when loading a million record table for an index , on initial creation
* of the index.
* @author doctor
*
* @param <K>
* @param <V>
*/
public class LHMap2BlockFileManager<K, V> implements
LHMap2.BlockListener<K, V>, Serializable {
/**
*
*/
private static final long serialVersionUID = 2615265603397988894L;
LHMap2BlockFileManagerData data = new LHMap2BlockFileManagerData(
new byte[10000], new Random(), 0, new ArrayList<Integer>(), 0);
public LHMap2BlockFileManager(File baseDir, String name, int maxBlocks,
double unloadRatio) {
data.home = new File(baseDir, name);
if (!data.home.exists())
data.home.mkdir();
this.data.maxBlocks = maxBlocks;
this.data.unloadRatio = unloadRatio;
}
@Override
public void blockRequested(int block, LHMap2<K, V> map) {
LHMap2.Block<K, V> b = map.blockList.get(block);
if (b == null) {
int tries = 3;
File f = new File(data.home, Integer.toString(block));
do {
if (f.exists())
break;
if (!f.exists()) {
if (--tries >= 0)
fatal(block);
try {
Thread.sleep(100);
} catch (InterruptedException e) {
e.printStackTrace();
}
}
} while (true);
try {
ByteArrayInputStream bis = new ByteArrayInputStream(data.buf);
FileInputStream fis = new FileInputStream(f);
int sz = fis.read(data.buf);
fis.close();
addByteStats(sz);
ObjectInputStream ois = new ObjectInputStream(bis);
b = new LHMap2.Block<K, V>();
b.readExternal(ois);
ois.close();
b.loadFromShadow(map);
map.blockList.set(block, b);
--data.retired;
} catch (FileNotFoundException e) {
e.printStackTrace();
fatal(block);
} catch (IOException e) {
e.printStackTrace();
fatal(block);
} catch (ClassNotFoundException e) {
e.printStackTrace();
fatal(block);
}
}
int size = map.blockList.size();
try {
long freeMemory = Runtime.getRuntime().freeMemory();
long limitMemory = (long) (data.avgBlockSize * data.unloadRatio * size);
if (block % 30 == 0)
System.err.println("free memory =" + freeMemory + " limit "
+ limitMemory);
if (map.split % 20 == 19) {
// this is just to add statistics before really needing to retire
retireRandomBlock(map, block);
++data.retired;
} else if (freeMemory < limitMemory) {
for (int i = 0; i < size / 4; ++i) {
retireRandomBlock(map, block);
++data.retired;
}
System.runFinalization();
System.gc();
}
} catch (FileNotFoundException e) {
e.printStackTrace();
} catch (IOException e) {
e.printStackTrace();
}
}
private void addByteStats(int sz) {
++data.avgCount;
data.avgBlockSize = (int) ((data.avgBlockSize
* (data.avgCount - 1) + sz) / data.avgCount);
}
public void retireRandomBlock(LHMap2<K, V> map, int notThisOne)
throws FileNotFoundException, IOException {
int pick = 0;
int size = map.blockList.size();
LHMap2.Block<K, V> b = null;
for (pick = 0; pick < size
&& (pick == notThisOne || (b = map.blockList.get(pick)) == null); ++pick)
;
if (pick < size)
retireOneBlock(map, pick, b);
}
private void retireOneBlock(LHMap2<K, V> map, int pick, LHMap2.Block<K, V> b)
throws IOException, FileNotFoundException {
if (b == null)
return;
if (b.isChanged()) {
// System.err.println("Retiring " + pick);
File f = new File(data.home, Integer.toString(pick));
ByteArrayOutputStream bos = new ByteArrayOutputStream();
ObjectOutputStream oos = new ObjectOutputStream(bos);
b.writeExternal(oos);
oos.flush();
oos.close();
FileOutputStream fos = new FileOutputStream(f);
byte[] bb = bos.toByteArray();
fos.write(bb);
fos.flush();
fos.close();
if (bb.length > data.buf.length) {
data.buf = bb;
}
}
map.blockList.set(pick, null);
b = null;
}
private void fatal(int block) {
Exception e = new Exception();
try {
throw e;
} catch (Exception e2) {
e2.printStackTrace();
}
System.err.println("block " + block
+ " requested and it is not in blocklist and not a file");
for (int i : data.retirees) {
System.err.print(i + " ");
}
System.err.println(" were retired");
System.exit(-2);
}
public static boolean metaExists(File indexDir, String name) {
File home = new File(indexDir, name);
return new File(home, "LinearMap2").exists();
}
public static <K, V> LHMap2<K, V> load(File baseDir, String name)
throws FileNotFoundException, IOException, ClassNotFoundException {
File home = new File(baseDir, name);
File f2 = new File(home, "LinearMap2");
ObjectInputStream ois = new ObjectInputStream(new FileInputStream(f2));
LHMap2<K, V> map = (LHMap2<K, V>) ois.readObject();
ois.close();
loadBlocks(map);
return map;
}
private static <K, V> void loadBlocks(LHMap2<K, V> map) {
LHMap2BlockFileManager<K, V> mgr = getBlockManagerListener(map);
int size = map.blockList.size();
for (int i = 0; i < size; ++i) {
mgr.blockRequested(i, map);
}
}
public static <K, V> LHMap2BlockFileManager<K, V> getBlockManagerListener(
LHMap2<K, V> map) {
LHMap2BlockFileManager<K, V> mgr = (LHMap2BlockFileManager<K, V>) map.listeners
.get(0);
return mgr;
}
public static void save(File indexDir, String name,
LHMap2<?, ?> offsetMap) throws FileNotFoundException, IOException {
retireAllBlocks(offsetMap);
File home = new File(indexDir, name);
File f2 = new File(home, "LinearMap2");
ObjectOutputStream oos = new ObjectOutputStream(
new FileOutputStream(f2));
oos.writeObject(offsetMap);
oos.close();
}
private static <K, V> void retireAllBlocks(LHMap2<K, V> offsetMap)
throws FileNotFoundException, IOException {
LHMap2BlockFileManager<K, V> mgr = getBlockManagerListener(offsetMap);
int sz = offsetMap.blockList.size();
for (int i = 0; i < sz; ++i) {
LHMap2.Block<K, V> b = offsetMap.blockList.get(i);
// offsetMap.blockList.set(i, null); // mark for reloading as block
// destroyed after writing
if (b != null) {
mgr.retireOneBlock(offsetMap, i, b);
}
}
}
}
package linearhashmap;
import java.io.File;
import java.io.Serializable;
import java.util.List;
import java.util.Random;
public class LHMap2BlockFileManagerData implements Serializable{
/**
*
*/
private static final long serialVersionUID = 1L;
public byte[] buf;
public Random r;
public File baseDir;
public File home;
public int maxBlocks;
public int retired;
public double unloadRatio;
public List<Integer> retirees;
public int avgBlockSize;
public long avgCount;
public LHMap2BlockFileManagerData(byte[] buf, Random r, int retired,
List<Integer> retirees, long avgCount) {
this.buf = buf;
this.r = r;
this.retired = retired;
this.retirees = retirees;
this.avgCount = avgCount;
}
}
参考文献
[edit | edit source]- ↑ 最简单的哈希表方案 - “带有线性探测的开放寻址”、“带有链表的独立链接”等等 - 在最坏情况下具有 O(n) 的查找时间,其中(意外地或恶意地)大多数键“冲突” - 大多数键被哈希到一个或几个桶中。其他哈希表方案 - “布谷鸟哈希”、“动态完美哈希”等等 - 即使在最坏情况下也能保证 O(1) 的查找时间。当插入一个新键时,这些方案会在必要时改变它们的哈希函数以避免冲突。
- ↑ 维基百科:编程语言比较(映射) 显示了多少编程语言提供哈希表功能。
集合在软件应用程序中是很有用的工具,正如在数学中一样,类似的抽象对象被聚合成集合。数学集合有一个相当简单的接口,可以用令人惊讶的多种方式实现。
Set<item-type> ADT
contains(test-item:item-type):Boolean- 如果 test-item 包含在集合中,则为 True。
insert(new-item:item-type)- 将 new-item 添加到集合中。
remove(item:item-type)- 从集合中删除 item。如果 item 不在集合中,此方法不执行任何操作。
remove(item-iter:List Iterator<item-type>)- 从集合中删除由 item-iter 标识的项目。
get-begin():List Iterator<item-type>- 允许迭代集合中的元素。
get-end():List Iterator<item-type>- 还允许迭代集合中的元素。
union(other:Set<item-type>):Set<item-type>- 返回一个集合,其中包含此集合或 other 集合中的所有元素。具有默认实现。
intersect(other:Set<item-type>):Set<item-type>- 返回一个集合,其中包含此集合和 other 集合中的所有元素。具有默认实现。
subtract(other:Set<item-type>):Set<item-type>- 返回一个集合,其中包含此集合中但不在 other 集合中的所有元素。具有默认实现。
is-empty():Boolean- 如果不再有项目可以弹出,并且没有栈顶项目,则为真。
get-size():Integer- 返回集合中的元素数量。
所有操作都可以在 时间内完成。
列表实现
[edit | edit source]有几种不同的方法来实现集合。最简单但大多数情况下效率最低的方法是简单地创建一个线性列表(数组、链表或类似结构),其中包含集合中的每个元素。对于最基本的操作,测试成员资格,可能的实现可能如下所示
function contains(List<T> list, T member)
for item in list
if item == member
return True
return False
要向此集合添加新成员,只需将元素添加到列表的开头或结尾。(如果进行检查以确保没有重复元素,则其他一些操作可能更简单。)其他操作可以类似地根据简单的列表操作来实现。不幸的是,成员资格测试的最坏情况运行时间为 ,如果该项不在列表中,甚至平均情况时间也是相同的,假设该项在列表中的任何位置的可能性都是相同的。如果集合很小,或者如果经常访问的项可以放在列表的前面,这可能是一个有效的解决方案,但其他选项的运行时间可能更快。
假设元素可以排序,并且插入和删除很少,则一个保证按排序顺序排列且没有重复元素的列表可以更高效。使用排序列表,成员资格测试可以高效到 的顺序。此外,并集、交集和差集可以在线性时间内实现,而使用无序列表则需要二次时间。
位数组实现
[edit | edit source]对于某些数据,维护一个描述集合内容的位数组可能更实用。在这种表示中,每个问题域元素都有一个 1 或 0,指定该对象是否是集合的元素。对于一个简单的情况,假设只有 0 到 n 的整数可以是集合的成员,其中 n 是事先知道的。这可以用长度为 n+1 的位数组来表示。contains 操作很简单
function contains(BitArray array, Int member)
if member >= length(array)
return False
else if array[member] == 1
return True
else
return False
要向这种集合添加或删除元素,只需修改位数组以反映该索引应为 1 或 0。成员资格在正好 (常数)时间内运行,但它的域非常有限。可以对域进行移位,从 m 到 n 以步长 k,而不是像上面指定的那样从 0 到 n 以步长 1,但这里没有太多灵活性。尽管如此,对于正确的域,这通常是最有效的解决方案。
位数组是存储布尔变量集的有效结构。一个例子是一组命令行选项,这些选项允许应用程序在运行时执行各种行为。C 及类似语言提供了按位运算符,使程序员能够在单个机器指令中访问位域,而数组访问通常需要两个或三个指令,包括内存读取操作。一个功能齐全的位集实现包括用于计算集合并集、集合交集、集合差集和元素值的运算符。[1]
关联数组实现
[edit | edit source]关联数组——即哈希表和二叉搜索树,代表了集合的一种重量级但通用的表示。二叉树通常具有 时间实现以用于查找和修改特定键,而哈希表具有 实现(尽管有一个更高的常数因子)。此外,它们能够存储几乎任何类型的键。成员资格测试很简单:只需测试潜在的集合成员是否作为关联数组中的键存在。要添加元素,只需将集合成员作为关联数组中的键添加,并使用一个虚拟值。在优化的实现中,可以编写一个专门的哈希表或二叉树,它不存储与键相对应的值,而不是重复使用现有的关联数组实现。这里的值没有意义,它们会占用一个常数因子的额外内存空间。
参考文献
[edit | edit source]- ↑ Samuel Harbison 和 Guy Steele。C:参考手册。2002 年。
在选择数据结构之前,全面了解需要解决的问题非常重要,因为每种结构都针对特定任务进行了优化。例如,哈希表有利于快速查找时间而不是内存使用,而数组则紧凑且不灵活。其他结构,例如堆栈,针对在整个程序执行过程中如何添加、删除和访问数据进行了优化以实施严格的规则。对数据结构的深刻理解是至关重要的,因为它为我们提供了以结构化方式思考程序行为的工具。
[TODO:] Use asymptotic behaviour to decide, most importantly seeing how the structure will be used: an infrequent operation does not need to be fast if it means everything else will be much faster
[TODO:] Can use a table like this one to compare the asymptotic behaviour of every structure for every operation on it.
| 数组 | 动态数组 | 数组双端队列 | 单链表 | 双向链表 | |
|---|---|---|---|---|---|
| 推入(前端) | - | O(n) | O(1) | O(1) | O(1) |
| 弹出(前端) | - | O(n) | O(1) | O(1) | O(1) |
| 推入(后端) | - | O(1) | O(1) | O(n),可能 O(1)* | O(1) |
| 弹出(后端) | - | O(1) | O(1) | O(n) | O(1) |
| 在(给定迭代器)之前插入 | - | O(n) | O(n) | O(n) | O(1) |
| 删除(给定迭代器) | O(n) | O(n) | O(n) | O(1) | |
| 在(给定迭代器)之后插入 | O(n) | O(n) | O(1) | O(1) | |
| 在(给定迭代器)之后删除 | - | O(n) | O(n) | O(1) | O(1) |
| 获取第 n 个元素(随机访问) | O(1) | O(1) | O(1) | O(n) | O(n) |
| 适合实现堆栈 | 否 | 是(后端是顶部) | 是 | 是(前端是顶部) | 是 |
| 适合实现队列 | 否 | 否 | 是 | 可能* | 是 |
| C++ STL | std::array
|
std::vector
|
std::deque
|
std::forward_list
|
std::list
|
| Java 集合 | java.util.Array
|
java.util.ArrayList
|
java.util.ArrayDeque
|
- | java.util.LinkedList
|
* singly-linked lists can push to the back in O(1) with the modification that you keep a pointer to the last node
| 排序数组 | 排序链表 | 自平衡二叉搜索树 | 哈希表 | |
|---|---|---|---|---|
| 查找键 | O(log n) | O(n) | O(log n) | 平均 O(1),最坏情况下 O(n) |
| 插入元素 | O(n) | O(n) | O(log n) | 平均 O(1),最坏情况下 O(n) |
| 删除键 | O(n) | O(n) | O(log n) | 平均 O(1),最坏情况下 O(n) |
| 删除元素(给定迭代器) | O(n) | O(1) | O(1) | O(1) |
| 可以按排序顺序遍历吗? | 是 | 是 | 是 | 否 |
| 需要 | 比较函数 | 比较函数 | 比较函数 | 哈希函数 |
| C++ STL | - | - | std::setstd::mapstd::multiset
|
std::unordered_setstd::unordered_mapstd::unordered_multiset
|
| Java 集合 | - | - | java.util.TreeSet
|
java.util.HashSet
|
- 请更正任何错误
| 二叉搜索 | AVL 树 | 二叉堆(最小) | 二项式队列(最小) | |
|---|---|---|---|---|
| 插入元素 | O(log n) | O(log n) | O(log n) | O(1)(平均) |
| 删除元素 | O(log n) | O(log n) | 不可用 | 不可用 |
| 删除最小元素 | O(log n) | O(log n) | O(log n) | O(log n) |
| 查找最小元素 | O(log n) | O(log n) | O(1) | O(log n)(如果指向最小的指针,则可以为 O(1)) |
| 增加键 | 不可用 | 不可用 | O(log n) | O(log n) |
| 减少键 | 不可用 | 不可用 | O(log n) | O(log n) |
| 查找 | O(log n) | O(log n) | 不可用 | 不可用 |
| 删除元素 | O(log n) | O(log n) | 不可用 | 不可用 |
| 创建 | O(1) | O(1) | O(1) | O(1) |
| 查找第 k 小元素 | O(log n) | O(log n) | O((k-1)*log n) | O(k*log n) |
| 哈希表(哈希映射) | |
|---|---|
| 设置值 | Ω(1), O(n) |
| 获取值 | Ω(1), O(n) |
| 删除 | Ω(1), O(n) |
[TODO:] Can also add a table that specifies the best structure for some specific need e.g. For queues, double linked. For stacks, single linked. For sets, hash tables. etc...
[TODO:] Could also contain table with space complexity information (there is a significative cost in using hashtables or lists implemented via arrays, for example).
























































































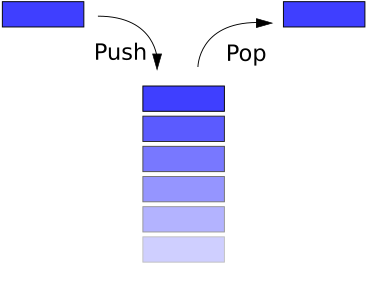






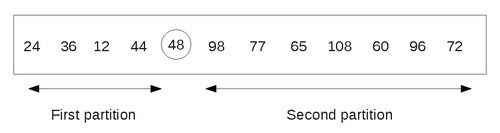




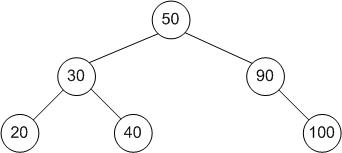





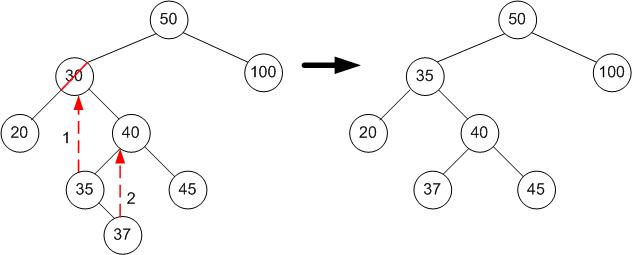
![{\displaystyle array[floor(N/2)]>array[N]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24c556c36e19d6cdca1424cc3846013f01027bb6)










![{\displaystyle \left(i,\left[1..n\right]\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/536da7d1241489aca63f932e0a87674ef50aa9ed)


