量子世界/费曼路线/从量子到经典

从量子到经典

作用量

让我们回到传播子

$\langle B|A\rangle =\int \!{\mathcal {DC}}\,Z[{\mathcal {C}}:A\rightarrow B].$

对于一个自由且稳定的粒子，我们发现

$Z[{\mathcal {C}}]=e^{-(i/\hbar )\,m\,c^{2}\,s[{\mathcal {C}}]},\qquad s[{\mathcal {C}}]=\int _{\mathcal {C}}ds,$

其中 $ds={\sqrt {dt^{2}-(dx^{2}+dy^{2}+dz^{2})/c^{2}}}$ 是与路径元素 $d{\mathcal {C}}$ 相关的固有时间隔。对于一般情况，我们发现振幅 $Z(d{\mathcal {C}})$ 是 $t,x,y,z$ 和 $dt,dx,dy,dz$ 的函数，或者等效地，是坐标 $t,x,y,z$、4-速度的组件 $c\,dt/ds,dx/ds,dy/ds,dz/ds$，以及 $ds$ 的函数。对于一个稳定但并非自由的粒子，我们通过与上述振幅相同的论证得到，

$Z[{\mathcal {C}}]=e^{(i/\hbar )\,S[{\mathcal {C}}]},$

我们已经引入了名为作用量的函数$S[{\mathcal {C}}]=\int _{\mathcal {C}}dS$。

对于一个自由且稳定的粒子，$S[{\mathcal {C}}]$ 是固有时间（或固有持续时间）$s[{\mathcal {C}}]=\int _{\mathcal {C}}ds$ 乘以 $-mc^{2}$，无穷小作用量 $dS[d{\mathcal {C}}]$ 与 $ds$ 成正比。

$S[{\mathcal {C}}]=-m\,c^{2}\,s[{\mathcal {C}}],\qquad dS[d{\mathcal {C}}]=-m\,c^{2}\,ds.$

让我们回顾一下。如果我们知道如何计算概率 $p(B|A)$（在所有情况下），我们就可以了解稳定粒子的所有运动。如果我们知道振幅 $\langle B|A\rangle$，我们就可以知道这一点。如果我们知道函数 $Z[{\mathcal {C}}]$，我们就可以知道后者。如果我们知道无穷小作用量 $dS(t,x,y,z,dt,dx,dy,dz)$ 或 $dS(t,\mathbf {r} ,dt,d\mathbf {r} )$（在所有情况下），我们就可以知道这个函数。

我们对 $dS$ 知道什么呢？

连续传播子的可乘性意味着相邻无穷小路径段 $d{\mathcal {C}}_{1}$ 和 $d{\mathcal {C}}_{2}$ 相关作用量的可加性。换句话说，

$e^{(i/\hbar )\,dS(d{\mathcal {C}}_{1}+d{\mathcal {C}}_{2})}=e^{(i/\hbar )\,dS(d{\mathcal {C}}_{2})}\,e^{(i/\hbar )\,dS(d{\mathcal {C}}_{1})}$

意味着

$dS(d{\mathcal {C}}_{1}+d{\mathcal {C}}_{2})=dS(d{\mathcal {C}}_{1})+dS(d{\mathcal {C}}_{2}).$

由此可见，微分 $dS$ 对微分 $dt,d\mathbf {r}$ 是齐次的（次数为 1）。

$dS(t,\mathbf {r} ,\lambda \,dt,\lambda \,d\mathbf {r} )=\lambda \,dS(t,\mathbf {r} ,dt,d\mathbf {r} ).$

$dS$ 的这一性质使我们能够将作用量 $S[{\mathcal {C}}]$ 视为与 ${\mathcal {C}}$ 相关的（特定于粒子的）长度，而将 $dS$ 视为定义了（特定于粒子的）时空几何。将 $1/dt$ 代入 $\lambda$，得到

$dS(t,\mathbf {r} ,\mathbf {v} )={\frac {dS}{dt}}.$

这似乎有些不对劲，不是吗？由于等式右侧现在是一个有限量，我们不应该对左侧使用符号 $dS$。我们实际上发现了一个函数 $L(t,\mathbf {r} ,\mathbf {v} )$，被称为 *拉格朗日函数*，使得 $dS=L\,dt$。

测地线方程

考虑从 $A$ 到 $B.$ 的时空路径 ${\mathcal {C}}$。让我们以这样一种方式改变（“变化”）它，即 ${\mathcal {C}}$ 的每个点 $(t,\mathbf {r} )$ 都向对应点 $(t+\delta t,\mathbf {r} +\delta \mathbf {r} ),$ 平移了无穷小的量，但端点保持固定：$\delta t=0$ 和 $\delta \mathbf {r} =0$ 在 $A$ 和 $B.$

如果 $t\rightarrow t+\delta t,$ 那么 $dt=t_{2}-t_{1}\longrightarrow t_{2}+\delta t_{2}-(t_{1}+\delta t_{1})=(t_{2}-t_{1})+(\delta t_{2}-\delta t_{1})=dt+d\delta t.$

同样地，$d\mathbf {r} \rightarrow d\mathbf {r} +d\delta \mathbf {r} .$

一般来说，变化 ${\mathcal {C}}\rightarrow {\mathcal {C}}'$ 会导致动作的相应变化：$S[{\mathcal {C}}]\rightarrow S[{\mathcal {C}}']\neq S[{\mathcal {C}}].$ 如果动作没有改变（也就是说，如果它在 ${\mathcal {C}}$ 处是 *静止的* ），

$\delta S=\int _{{\mathcal {C}}'}dS-\int _{\mathcal {C}}dS=0,$

那么 ${\mathcal {C}}$ 是由 $dS.$ 定义的几何的 *测地线*。（函数 $f(x)$ 在 $x$ 的这些值处是静止的，当 $x$ 无限小变化时，它的值不会改变。同样，我们称泛函 $S[{\mathcal {C}}]$ 是静止的，如果它的值不会改变，当 ${\mathcal {C}}$ 无限小变化。）

为了得到一种更方便的方法来表征测地线，我们从扩展开始

$dS({\mathcal {C}}')=dS(t+\delta t,\mathbf {r} +\delta \mathbf {r} ,dt+d\delta t,d\mathbf {r} +d\delta \mathbf {r} )$

$=dS(t,\mathbf {r} ,dt,d\mathbf {r} )+{\frac {\partial dS}{\partial t}}\,\delta t+{\frac {\partial dS}{\partial \mathbf {r} }}\cdot \delta \mathbf {r} +{\frac {\partial dS}{\partial dt}}\,d\delta t+{\frac {\partial dS}{\partial d\mathbf {r} }}\cdot d\delta \mathbf {r} .$

这给了我们

$(^{*})\quad \int _{{\mathcal {C}}'}dS-\int _{\mathcal {C}}dS=\int _{\mathcal {C}}\left[{\partial dS \over \partial t}\delta t+{\partial dS \over \partial \mathbf {r} }\cdot \delta \mathbf {r} +{\partial dS \over \partial dt}d\,\delta t+{\partial dS \over \partial d\mathbf {r} }\cdot d\,\delta \mathbf {r} \right].$

接下来我们使用导数的乘积规则，

$d\left({\partial dS \over \partial dt}\delta t\right)=\left(d{\partial dS \over \partial dt}\right)\delta t+{\partial dS \over \partial dt}d\,\delta t,$

$d\left({\partial dS \over \partial d\mathbf {r} }\cdot \delta \mathbf {r} \right)=\left(d{\partial dS \over \partial d\mathbf {r} }\right)\cdot \delta \mathbf {r} +{\partial dS \over \partial d\mathbf {r} }\cdot d\,\delta \mathbf {r} ,$

用来替换(*)中的最后两项，这将我们带到

$\delta S=\int \left[\left({\partial dS \over \partial t}-d{\partial dS \over \partial dt}\right)\delta t+\left({\partial dS \over \partial \mathbf {r} }-d{\partial dS \over \partial d\mathbf {r} }\right)\cdot \delta \mathbf {r} \right]+\int d\left({\partial dS \over \partial dt}\delta t+{\partial dS \over \partial d\mathbf {r} }\cdot \delta \mathbf {r} \right).$

第二个积分消失是因为它等于括号内表达式在端点 $A$ 和 $B,$ 处的差值，其中 $\delta t=0$ 并且 $\delta \mathbf {r} =0.$ 如果 ${\mathcal {C}}$ 是测地线，那么第一个积分也消失了。事实上，在这种情况下，$\delta S=0$ 必须对所有可能的（无穷小）变化 $\delta t$ 和 $\delta \mathbf {r} ,$ 成立，因此第一个积分的被积函数消失。底线是，由 $dS$ 定义的测地线满足测地线方程

${\partial dS \over \partial t}=d\,{\partial dS \over \partial dt},\qquad {\partial dS \over \partial \mathbf {r} }=d\,{\partial dS \over \partial d\mathbf {r} }.$

最小作用原理

如果一个物体从 $A$ 运动到 $B,$ 它沿着从 $A$ 到 $B,$ 的所有路径运动，与电子穿过两条缝的方式相同。那么，为什么大的物体（如行星、网球或蚊子）似乎沿着一条单一且明确的路径运动呢？

至少有两个原因。其中一个原因是，物体越大，越难满足规则$B.$ 中规定的条件。另一个原因是，即使满足这些条件，找到质量为$m$ 的物体的可能性，根据经典物理定律，它不应该存在，随着$m$ 的增加而降低。

为了看到这一点，我们需要考虑到一个从$A$ 运动到$B,$ 的物体，严格来说不可能检查它是否沿着数学上精确的路径${\mathcal {C}}.$ 运动。让我们做一个半现实的假设，即我们可以检查的是，一个物体是否在一条狭窄的路径束内从$A$ 运动到$B$ — 这些路径包含在一个狭窄的管道${\mathcal {T}}.$ 内。找到它已经运动到$B$ 的概率是路径积分$I({\mathcal {T}})=\int _{\mathcal {T}}{\mathcal {DC}}e^{(i/\hbar )S[{\mathcal {C}}]},$ 的绝对平方，它对${\mathcal {T}}.$ 中包含的路径求和。

让我们假设从$A$ 到$B$ 恰好只有一条路径，对于该路径，$S[{\mathcal {C}}]$ 是固定的：无论我们如何稍微改变路径，它的长度都不会改变。换句话说，我们假设只有一条测地线。让我们称它为${\mathcal {G}},$，并假设它位于${\mathcal {T}}.$ 内。

无论路径${\mathcal {C}},$ 如何变化，相位 $S[{\mathcal {C}}]/\hbar$ 在${\mathcal {G}}.$ 处将保持静止。这意味着，宽泛地说，大量靠近${\mathcal {G}}$ 的路径对$I({\mathcal {T}})$ 的贡献具有几乎相同的相位。因此，相应相位因子$e^{(i/\hbar )S[{\mathcal {C}}]}$ 之和的幅度很大。

如果$S[{\mathcal {C}}]/\hbar$ 在${\mathcal {C}},$ 处不保持静止，则取决于它在${\mathcal {C}}.$ 变化时变化的速度。如果变化速度足够快，则与靠近${\mathcal {C}}$ 的路径相关的相位或多或少地均匀地分布在区间$[0,2\pi ],$ 上，因此相应的相位因子加起来得到一个幅度相对较小的复数。在极限$S[{\mathcal {C}}]/\hbar \rightarrow \infty ,$ 中，对$I({\mathcal {T}})$ 的唯一显著贡献来自${\mathcal {G}}.$ 无穷小邻域内的路径。

我们假设 ${\mathcal {G}}$ 位于 ${\mathcal {T}}.$ 。如果它不在，并且如果 $S[{\mathcal {C}}]/\hbar$ 变化足够快，则与 ${\mathcal {T}}$ 中任何路径附近的路径相关的相位在间隔 $[0,2\pi ],$ 上或多或少地均匀分布，因此在极限 $S[{\mathcal {C}}]/\hbar \rightarrow \infty$ 中，对 $I({\mathcal {T}}).$ 没有显著的贡献。

正如你所记得的，对于自由粒子， $S[{\mathcal {C}}]=-m\,c^{2}\,s[{\mathcal {C}}].$ 从中我们可以得出，在根据经典物理定律不应该存在的地方找到一个自由运动的物体的可能性，随着其质量的增加而降低。由于对于足够重的物体，由于运动的影响而导致的动作贡献相对于 $|-m\,c^{2}\,s[{\mathcal {C}}]|,$ 很小，对于不自由运动的物体也是如此。

那么，什么是经典物理定律？

它们是量子物理定律在极限 $\hbar \rightarrow 0.$ 中退化的形式。在这个极限下，正如你从上面所了解到的，发现一个粒子在一个包含测地线的管子（无论有多窄）中运动的概率是 1，而发现一个粒子在一个不包含测地线的管子（无论有多宽）中运动的概率是 0。因此，我们可以通过说它遵循由 $dS.$ 定义的几何的测地线来陈述经典物理定律（首先是单个“点质量”）。

这很容易推广。一个具有 $n$ 个自由度的系统（例如，一个具有 $m$ 个粒子的系统，具有 $n=3m$ 个自由度）的传播子是

$\langle {\mathcal {P}}_{f},t_{f}|{\mathcal {P}}_{i},t_{i}\rangle =\int \!{\mathcal {DC}}\,e^{(i/\hbar )S[{\mathcal {C}}]},$

其中 ${\mathcal {P}}_{i}$ 和 ${\mathcal {P}}_{f}$ 分别是系统在初始时刻 $t_{i}$ 和最终时刻 $t_{f},$ 的系统配置，积分是对系统 $n{+}1$ 维配置时空中所有从 $({\mathcal {P}}_{i},t_{i})$ 到 $({\mathcal {P}}_{f},t_{f}).$ 在这种情况下，相应的经典系统遵循由作用量微分 $dS,$ 定义的几何的测地线，作用量微分现在依赖于 $n$ 个空间坐标，一个时间坐标和相应的 $n{+}1$ 个微分。

经典系统遵循其作用量定义的几何的测地线的论断通常被称为最小作用量原理。更恰当的名称是驻定作用量原理。

能量和动量

观察到，如果 $dS$ 不依赖于 $t$ （也就是说，$\partial dS/\partial t=0$ ）那么

$E=-{\partial dS \over \partial dt}$

沿着测地线是常数。（我们很快就会发现负号的原因。）

同样，如果 $dS$ 不依赖于 $\mathbf {r}$ （也就是说，$\partial dS/\partial \mathbf {r} =0$ ）那么

$\mathbf {p} ={\partial dS \over \partial d\mathbf {r} }$

沿着测地线是常数。

$E$ 告诉我们投影 $dt$ 的线段 $d{\mathcal {C}}$ 在路径 ${\mathcal {C}}$ 上，对时间轴上的作用有多少贡献 ${\mathcal {C}}.$ $\mathbf {p}$ 告诉我们投影 $d\mathbf {r}$ 的 $d{\mathcal {C}}$ 在空间上的投影对 $S[{\mathcal {C}}].$ 如果 $dS$ 没有显式的时间依赖性，那么时间轴上的等间隔对 $S[{\mathcal {C}}],$ 做出相同的贡献，如果 $dS$ 没有显式空间依赖性，那么任何空间轴上的等间隔对 $S[{\mathcal {C}}].$ 在前一种情况下，等时间间隔是物理等价的：它们表示等时间。在后一种情况下，等空间间隔是物理等价的：它们表示等距离。

如果时间坐标的等间隔或空间坐标的等间隔不是物理等价的，那么这有两种原因。第一个是使用了非惯性坐标。因为如果使用惯性坐标，那么每个自由移动的点质量在时间坐标的等间隔内，都会在空间坐标上移动等间隔，这意味着等坐标间隔是物理等价的。第二个是，无论移动的是什么，它都不是自由移动的：无论什么，无论如何，都会影响它的运动。这是因为将物体运动的影响纳入量子物理数学形式主义的一种方法是，通过让 $dS$ 依赖于 $t$ 和/或 $\mathbf {r} .$ 来使惯性坐标间隔在物理上不等价。

因此，对于自由运动的经典物体，$E$ 和 $\mathbf {p}$ 都是常数。由于 $E$ 的恒定性源于坐标时间等间隔的物理等效性（也称为时间的“齐性”），并且由于（经典地）能量被定义为其恒定性由时间的齐性所暗示的量，$E$ 是物体的能量。

同样，由于 $\mathbf {p}$ 的恒定性源于任何空间坐标轴等间隔的物理等效性（也称为空间的“齐性”），并且由于（经典地）动量被定义为其恒定性由空间的齐性所暗示的量，$\mathbf {p}$ 是物体的动量。

让我们对先前结果进行微分。

$dS(t,\mathbf {r} ,\lambda \,dt,\lambda \,d\mathbf {r} )=\lambda \,dS(t,\mathbf {r} ,dt,d\mathbf {r} ),$

关于 $\lambda .$ 左侧变为

${d(dS) \over d\lambda }={\partial dS \over \partial (\lambda dt)}{\partial (\lambda dt) \over \partial \lambda }+{\partial dS \over \partial (\lambda d\mathbf {r} )}\cdot {\partial (\lambda d\mathbf {r} ) \over \partial \lambda }={\partial dS \over \partial (\lambda dt)}dt+{\partial dS \over \partial (\lambda d\mathbf {r} )}\cdot d\mathbf {r} ,$

而右侧则仅为 $dS.$ 将 $\lambda =1$ 代入，并使用上面对 $E$ 和 $\mathbf {p} ,$ 的定义，我们得到

$-E\,dt+\mathbf {p} \cdot d\mathbf {r} =dS.$

$dS=-m\,c^{2}\,ds$ 是一个四维标量。 由于 $(c\,dt,d\mathbf {r} )$ 是一个四维向量的分量，等式左侧，$-E\,dt+\mathbf {p} \cdot d\mathbf {r} ,$ 当且仅当 $(E/c,\mathbf {p} )$ 是另一个四维向量的分量。

(如果我们没有定义 $E$ 没有负号，那么这个四维向量将具有分量 $(-E/c,\mathbf {p} ).$)

在自由质点的静止系 ${\mathcal {F}}'$ 中，$dt'=ds$ 并且 $dS=-m\,c^{2}\,dt'.$ 使用 洛伦兹变换，我们发现这等于

$dS=-mc^{2}{dt-v\,dx/c^{2} \over {\sqrt {1-v^{2}/c^{2}}}}=-{mc^{2} \over {\sqrt {1-v^{2}/c^{2}}}}\,dt+{m\mathbf {v} \over {\sqrt {1-v^{2}/c^{2}}}}\cdot d\mathbf {r} ,$

其中 $\mathbf {v} =(v,0,0)$ 是质点在 ${\mathcal {F}}.$ 中的速度。 将其与上面框起来的公式进行比较，我们发现对于一个自由质点，

$E={mc^{2} \over {\sqrt {1-v^{2}/c^{2}}}}\qquad \mathbf {p} ={m\mathbf {v} \over {\sqrt {1-v^{2}/c^{2}}}}\;.$

洛伦兹力定律

为了将作用对粒子运动的影响（无论其原因）考虑在内，我们必须修改自由粒子与路径段相关联的作用微分 $dS=-mc^{2}\,dt{\sqrt {1-v^{2}/c^{2}}}$。在这样做的时候，我们必须注意，修改后的 $dS$ (i) 仍然是 微分齐次的，并且 (ii) 仍然是一个四维标量。最直接的方法是添加一个不仅是齐次的，而且在坐标微分中是线性的项

$(^{*})\quad dS=-mc^{2}\,dt{\sqrt {1-v^{2}/c^{2}}}-qV(t,\mathbf {r} )\,dt+(q/c)\mathbf {A} (t,\mathbf {r} )\cdot d\mathbf {r} .$

信不信由你，所有经典电磁效应（而不是它们的原因）都可以用这个表达式来解释。 $V(t,\mathbf {r} )$ 是一个标量场（即，在空间坐标旋转下保持不变的时间和空间坐标函数）， $\mathbf {A} (t,\mathbf {r} )$ 是一个三维矢量场，而 $(V,\mathbf {A} )$ 是一个四维矢量场。我们将 $V$ 和 $\mathbf {A}$ 分别称为标量势和矢量势。粒子特定的常数 $q$ 是电荷，它决定了特定种类的粒子受到电磁影响的强度。

如果一个点质量不是自由的，那么上一节末尾的表达式给出了它的动能$E_{k}$和它的动量$\mathbf {p} _{k}.$将(*)写成以下形式

$dS=-(E_{k}+qV)\,dt+[\mathbf {p} _{k}+(q/c)\mathbf {A} ]\cdot d\mathbf {r}$

并将它代入定义

$(^{*}{}^{*})\quad E=-{\partial dS \over \partial dt},\qquad \mathbf {p} ={\partial dS \over \partial d\mathbf {r} },$

我们得到

$E=E_{k}+qV,\qquad \mathbf {p} =\mathbf {p} _{k}+(q/c)\mathbf {A} .$

$qV$和$(q/c)\mathbf {A}$分别是粒子的势能和势动量。

现在我们将(**)代入测地线方程

${\partial dS \over \partial \mathbf {r} }=d\,{\partial dS \over \partial d\mathbf {r} }.$

对于右手边，我们得到

$d\mathbf {p} _{k}+{q \over c}d\mathbf {A} =d\mathbf {p} _{k}+{q \over c}\left[dt{\partial \mathbf {A} \over \partial t}+\left(d\mathbf {r} \cdot {\partial \over \partial \mathbf {r} }\right)\mathbf {A} \right],$

而左手边则计算为

$-q{\partial V \over \partial \mathbf {r} }dt+{q \over c}{\partial (\mathbf {A} \cdot d\mathbf {r} ) \over \partial \mathbf {r} }=-q{\partial V \over \partial \mathbf {r} }dt+{q \over c}\left[\left(d\mathbf {r} \cdot {\partial \over \partial \mathbf {r} }\right)\mathbf {A} +d\mathbf {r} \times \left({\partial \over \partial \mathbf {r} }\times \mathbf {A} \right)\right].$

两项抵消，最终结果为

$d\mathbf {p} _{k}=q\underbrace {\left(-{\partial V \over \partial \mathbf {r} }-{1 \over c}{\partial \mathbf {A} \over \partial t}\right)} _{\displaystyle \equiv \mathbf {E} }dt+d\mathbf {r} \times {q \over c}\underbrace {\left({\partial \over \partial \mathbf {r} }\times \mathbf {A} \right)} _{\displaystyle \equiv \mathbf {B} }=q\,\mathbf {E} \,dt+d\mathbf {r} \times {q \over c}\,\mathbf {B} .$

当一个经典物体沿着测地线的段 $d{\mathcal {G}}$ 行进时，它的动量变化由两项之和决定，一项与 $d{\mathcal {G}}$ 的时间分量 $dt$ 成正比，另一项与空间分量 $d\mathbf {r} .$ 成正比。 $dt$ 对 $\mathbf {p} _{k}$ 的变化贡献取决于电场 $\mathbf {E} ,$ 而 $d\mathbf {r}$ 的贡献取决于磁场 $\mathbf {B} .$ 最后一个方程通常写成以下形式

${d\mathbf {p} _{k} \over dt}=q\,\mathbf {E} +{q \over c}\,\mathbf {v} \times \mathbf {B} ,$

称为洛伦兹力定律，并伴随以下叙述：存在一个称为电磁场的物理实体，它无处不在，并对电荷施加电场力$q$ $q\mathbf {E}$ 和磁场力$(q/c)\,\mathbf {v} \times \mathbf {B} .$

(注意：洛伦兹力定律的这种形式是在高斯单位制中成立的。在MKSA 单位制中，$c$ 消失了。）

经典的故事从何而来呢？

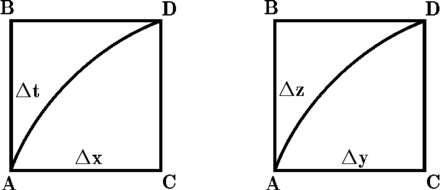
想象一个时空中有一个小矩形，其顶点为

$A=(0,0,0,0),\;B=(dt,0,0,0),\;C=(0,dx,0,0),\;D=(dt,dx,0,0).$

让我们计算从$A$ 到 $D$ 经 $B$ 路径的单位电荷 ($q=1$) 在自然单位中 ( $c=1$ )

$S_{ABD}=-V(dt/2,0,0,0)\,dt+A_{x}(dt,dx/2,0,0)\,dx$

$\quad =-V(dt/2,0,0,0)\,dt+\left[A_{x}(0,dx/2,0,0)+{\partial A_{x} \over \partial t}dt\right]dx.$

接下来，从 $A$ 到 $D$ 经过 $C$ 的路径对作用的贡献。

$S_{ACD}=A_{x}(0,dx/2,0,0)\,dx-V(dt/2,dx,0,0)\,dt$

$=A_{x}(0,dx/2,0,0)\,dx-\left[V(dt/2,0,0,0)+{\partial V \over \partial x}dx\right]dt.$

观察差异

$\Delta S=S_{ACD}-S_{ABD}=\left(-{\partial V \over \partial x}-{\partial A_{x} \over \partial t}\right)dt\,dx=E_{x}\,dt\,dx.$

或者，你可以将 $\Delta S$ 看作是回路 $A\rightarrow B\rightarrow D\rightarrow C\rightarrow A.$ 的电磁作用贡献。

让我们重复计算一个具有以下角点的矩形：

$A=(0,0,0,0),\;B=(0,0,dy,0),\;C=(0,0,0,dz),\;D=(0,0,dy,dz).$

$S_{ABD}=A_{z}(0,0,0,dz/2)\,dz+A_{y}(0,0,dy/2,dz)\,dy$

$=A_{z}(0,0,0,dz/2)\,dz+\left[A_{y}(0,0,dy/2,0)+{\partial A_{y} \over \partial z}dz\right]dy,$

$S_{ACD}=A_{y}(0,0,dy/2,0)\,dy+A_{z}(0,0,dy,dz/2)\,dz$

$=A_{y}(0,0,dy/2,0)\,dy+\left[A_{z}(0,0,0,dz/2)+{\partial A_{z} \over \partial y}dy\right]dz,$

$\Delta S=S_{ACD}-S_{ABD}=\left({\partial A_{z} \over \partial y}-{\partial A_{y} \over \partial z}\right)dy\,dz=B_{x}\,dy\,dz.$

因此，该环路的动作的电磁贡献等于 $\mathbf {B}$ 穿过该环路的通量。

记住 (i) 斯托克斯定理 和 (ii) $\mathbf {B}$ 的 定义（用 $\mathbf {A} ,$ 表示），我们发现

$\oint _{\partial \Sigma }\mathbf {A} \cdot d\mathbf {r} =\int _{\Sigma }{\hbox{curl}}\,\mathbf {A} \cdot d\mathbf {\Sigma } =\int _{\Sigma }\mathbf {B} \cdot d\mathbf {\Sigma } .$

换句话说，穿过一个环路 $\partial \Sigma$（或穿过任何由 $\partial \Sigma$ 包围的表面 $\Sigma$）的磁通量等于 $\mathbf {A}$ 在该环路（或任何由该环路包围的表面）周围的环流。

在有限的矩形$A\rightarrow B\rightarrow D\rightarrow C\rightarrow A$ 周围进行的循环$\oint _{\partial \Sigma }\mathbf {A} \cdot d\mathbf {r}$ 的作用，是增加（或减少）与线段$A\rightarrow B\rightarrow D$ 相关的动作，相对于与线段$A\rightarrow C\rightarrow D.$ 相关的动作。如果这两个线段的动作相等，那么我们可以预期从$A$ 到$D$ 的最小作用路径是一条直线。如果一个线段的动作大于另一个线段的动作，那么我们可以预期从$A$ 到$D$ 的最小作用路径会偏离动作较大的线段。

将这与经典故事进行比较，经典故事通过调用垂直于磁场和粒子运动方向的力来解释带电粒子在磁场中的路径弯曲。对同一效应的量子力学处理没有提供这样的解释。量子力学没有调用任何机制。它只是告诉我们，对于从$A$ 到$D,$ 行进的足够重的电荷，找到它在任何不包含连接$A$ 与$D,$ 的作用测地线的路径束中的概率几乎为零。

对于经典故事，它根据带电粒子在时空平面中的路径弯曲是由于作用在电场方向上的力而引起的，也是如此。（观察时空平面中的弯曲相当于加速或减速。特别是，包含$x$ 轴的时空平面中的弯曲相当于平行于$x$ 轴的方向的加速。）在这种情况下，相应的循环是 4 向量势$(cV,\mathbf {A} )$ 在时空循环周围的循环。