波/2-3D 问题

波 : 2 维和 3 维波
1 - 2 - 3 - 4 - 5 - 6 - 7
问题

问题

点 A 在原点。点 B 距离 A $3{\mbox{ m}}$ $3{\mbox{ m}}$ ，相对于 $x$ $x$ 轴逆时针方向 $30^{\circ }$ $30^{\circ }$ 。点 C 距离 A $2{\mbox{ m}}$ $2{\mbox{ m}}$ ，相对于 $x$ $x$ 轴逆时针方向 $100^{\circ }$ $100^{\circ }$ 。
1. 求从 A 到 B 的向量 ${\mbox{D}}_{1}$ 和从 A 到 C 的向量 ${\mbox{D}}_{2}$ 的笛卡尔坐标。
2. 求从 B 到 C 的向量 ${\mbox{D}}_{3}$ 的笛卡尔坐标。
3. 求 ${\mbox{D}}_{3}$ 的方向和大小。
对于上一问题中的向量，分别使用点积的余弦形式和笛卡尔形式求 ${\mbox{D}}_{1}\cdot {\mbox{D}}_{2}$ 。检查两个答案是否相同。
用图形或其他方法证明 $\vert {\mbox{A}}+{\mbox{B}}\vert \neq \vert {\mbox{A}}\vert +\vert {\mbox{B}}\vert$ ，除非向量 ${\mbox{A}}$ 和 ${\mbox{B}}$ 平行。
在 $x$ $x$ - $y$ $y$ 平面上定义的波形由 $h=h_{0}\sin({\mbox{k}}\cdot {\mbox{x}})$ $h=h_{0}\sin({\mbox{k}}\cdot {\mbox{x}})$ 定义，其中 ${\mbox{k}}=(1,2){\mbox{ cm}}^{-1}$ ${\mbox{k}}=(1,2){\mbox{ cm}}^{-1}$ 。
1. 在一张方格纸上画出 $x$ 和 $y$ 轴，然后绘制一条穿过原点并平行于向量 ${\mbox{k}}$ 的直线。
2. 在同一个图上绘制由 ${\mbox{k}}\cdot {\mbox{x}}=k_{x}x+k_{y}y=0$ 、 ${\mbox{k}}\cdot {\mbox{x}}=\pi$ 和 ${\mbox{k}}\cdot {\mbox{x}}=2\pi$ 定义的直线。检查这些直线是否垂直于 ${\mbox{k}}$ 。
两个相同频率 $\omega$ $\omega$ 的深海平面波，大约向东移动。然而，其中一个波向东偏了 $\beta$ $\beta$ 度北，另一个波向东偏了 $\beta$ $\beta$ 度南。
1. 确定这两个波之间干涉加强线的方向。
2. 确定干涉加强线之间的间距。
图 2.20 图示了色散关系的示例，其中频率是波矢幅度和方向的函数。
1. 对于三个波矢中的每一个，波的相速度是多少？提示：您可能需要通过图形方法获得每个波矢的长度。
2. 对于每个波矢，波前的方向是什么？
3. 对于每个图示的波矢，绘制另外两个波矢，它们的平均值为图示的波矢，并且它们的顶点位于相同的频率等高线上。确定由叠加的平面波产生的干涉加强线的方向，对于每个波矢对，它们都是波矢。

Figure 2.20: Graphical representation of the dispersion relation for shallow water waves

图 2.20：在

x

方向流动的河流中浅水波的色散关系的图形表示。频率的单位是赫兹，波数的单位是每米。

两个重力波具有相同的频率，但波长略有不同。
1. 如果一个波的方向角为 $\theta =\pi /4{\mbox{ radians}}$ ，另一个波的方向角是多少？（参见图 2.6。）
2. 确定这两个波之间干涉加强线的方向。
平面波入射到单缝上，在缝隙后散射出半角为 $\alpha$ 的光。如果整个装置浸没在折射率为 $n=1.5$ 的液体中，光的散射角将如何改变？(提示：回想一下透明介质中的折射率是真空中的光速与介质中的光速之比。此外，当光从真空进入透明介质时，光的频率不变。因此，光的波长将如何改变？)
确定需要多少直径的望远镜才能分辨出距离地球 $6{\mbox{ light years}}$ 的一颗恒星的 $2\times 10^{8}{\mbox{ km}}$ 的行星。(假设蓝光，其波长为 $\lambda \approx 4\times 10^{-7}{\mbox{ m}}=400{\mbox{ nm}}$ 。此外，出于本题目的考虑，不用担心两者之间亮度的巨大差异。)
地球上的激光发射器发出的激光束被月球上的角反射器反射回地球。
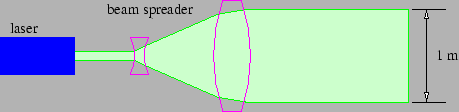
1. 工程师发现，如果激光束最初由图 2.21 所示的束扩束器扩散，则返回信号更强。解释一下为什么是这样。
2. 光束离开地球时的直径为 $1{\mbox{ m}}$ 。它到达距离地球 $4\times 10^{5}{\mbox{ km}}$ 的月球时有多宽？假设光的波长为 $5\times 10^{-7}{\mbox{ m}}$ 。
3. 如果激光束没有最初通过束扩束器，它在月球上的宽度会是多少？假设其初始直径为 $1{\mbox{ cm}}$ 。

Figure 2.21: Sketch of a beam expander for a laser

图 2.21: 激光束扩束器的示意图。

假设平面波以一定角度照射到障碍物上的两个缝隙，使得一个缝隙处的波相位滞后于另一个缝隙处的波相位半个波长。由此产生的干涉图样与没有滞后情况下的干涉图样有何不同？
假设一块折射率为 $n=1.33$ $n=1.33$ 的薄玻璃片放置在双缝衍射装置中一个缝隙的前面。
1. 玻璃片需要多厚才能使入射波减速，使其滞后于穿过另一个缝隙的波的相位差为 $\pi$ ？假设光的波长为 $\lambda =6\times 10^{-7}{\mbox{ m}}$ 。
2. 对于上述情况，描述一个缝隙前面没有玻璃片的情况下的衍射图样是如何定性变化的。解释你的结果。
一个光源发出两种波长， $\lambda _{1}=400{\mbox{ nm}}$ $\lambda _{1}=400{\mbox{ nm}}$ （蓝色）和 $\lambda _{2}=600{\mbox{ nm}}$ $\lambda _{2}=600{\mbox{ nm}}$ （红色）。
1. 定性地描绘这个光源通过双缝衍射产生的衍射图样。分别描绘每个波长的衍射图样。
2. 定性地描绘这个光源通过16缝衍射产生的衍射图样，其中缝间距与双缝情况相同。
一个光源发出两种波长， $\lambda _{1}=631{\mbox{ nm}}$ 和 $\lambda _{2}=635{\mbox{ nm}}$ 。为了区分这两种波长，光栅光谱仪至少需要多少条狭缝？（假设观察第一级衍射峰）。画出每个波长的衍射峰，并标出为了区分它们，峰需要多窄。