波/双缝衍射

波 : 二维和三维波
1 - 2 - 3 - 4 - 5 - 6 - 7
问题

两条缝隙

窄缝

图 2.16: 光线穿过缝隙 B 传播到屏幕的距离比穿过缝隙 A 的光线多。该距离为 $\Delta l=d\sin \theta$

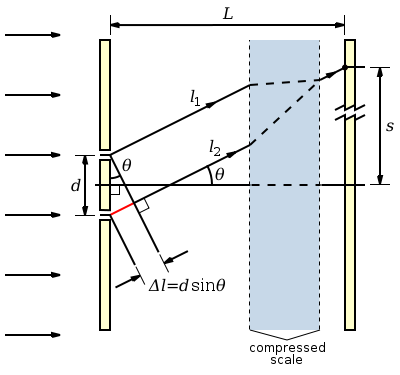
现在让我们想象一个平面正弦波垂直入射到一个带有两个窄缝的屏幕上，这两个窄缝的间距为d，如图 2.16 所示。由于缝隙相对于入射波的波长很窄，光束的扩展角度很大，每个缝隙单独产生的衍射图样都是一个向各个方向扩展的圆柱形波，如图 2.13 所示。来自两个缝隙的圆柱形波发生干涉，导致图 2.16 右侧屏幕上的波强度发生振荡。

当两条光线的路径长度差是波长λ的整数倍时，就会发生相长干涉。

[相长干涉条件]

$l_{2}-l_{1}=m\lambda ,\quad m=0,\pm 1,\pm 2,\ldots \,$

同样，相消干涉发生在

[相消干涉条件]

$l_{2}-l_{1}=\left(m+{\frac {1}{2}}\right)\lambda ,\quad m=0,\pm 1,\pm 2,\ldots \,$

如果缝隙到屏幕的距离L远大于缝隙间距d，则光线l₁和l₂近似平行，我们可以说路径长度差为

[L >> d时的路径长度差]

$l_{2}-l_{1}=d\sin \theta \,$

将这两个等式代入得到以下相长干涉条件

[相长干涉条件]

$d\sin \theta =m\lambda ,\quad m=0,\pm 1,\pm 2,\ldots \,$

整数m称为干涉级，表示两条路径差的波长数。在对应于整数m的每个角度上，相长干涉将最大，形成一个“条纹”。

屏幕上的一个点到中心线的距离s与θ的关系如下

$\tan \theta ={\frac {s}{L}}$

当θ很小时，我们可以说

$\tan \theta \approx \sin \theta$

因此我们可以将屏幕上的位置和条纹角度的表达式等同起来

${\frac {m\lambda }{d}}\approx {\frac {s}{L}}$

重新排列得到条纹间距的表达式

$s\approx {\frac {m\lambda L}{d}}$

要使此近似值有效，必须满足以下条件

• 缝隙到屏幕的距离L必须远大于缝隙间距d。
• 缝隙到条纹的角度θ必须很小。
• 缝隙必须比波长λ窄。

例子

让我们考虑一个具有以下参数的设置

• d = 0.1 mm
• λ = 2500 nm（红外线）

我们预计在 10 米处看到条纹间距为

$s={\frac {\lambda L}{d}}={\frac {2500\times 10^{-9}\times 10}{0.1\times 10^{-3}}}=0.25m$

首先，让我们看一下波在某个时刻的“快照”。点 (x,y) 的振幅由下式给出

$u(x,y,t)=a\sin \left(k{\sqrt {\left(x-{\frac {d}{2}}\right)^{2}+y^{2}}}\right)+a\sin \left(k{\sqrt {\left(x+{\frac {d}{2}}\right)^{2}+y^{2}}}\right)$

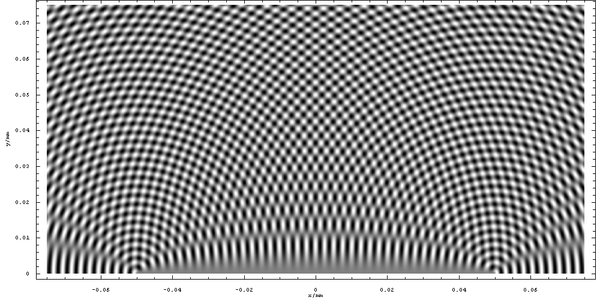
其中 k 是波数，由 2π/λ给出。在本练习中，我们将忽略随着距离衰减的振幅，因此条纹在整个空间中都保持明亮。下图显示了该函数的图。您可以清楚地看到每个光源的圆形传播，但很难辨认出整体条纹结构。

现在，人眼和所有光测量设备都没有检测到光波的单个振荡，它们测量的是强度。在这里，强度是两个光源之间相位差的函数，而相位差又与路径长度差直接相关。

$\delta ={\frac {2\pi }{\lambda }}\Delta l$

$I\approx 4a^{2}\cos ^{2}{\frac {\delta }{2}}$

下图显示了该强度函数。我们看到一个非常清晰的条纹结构被揭示出来

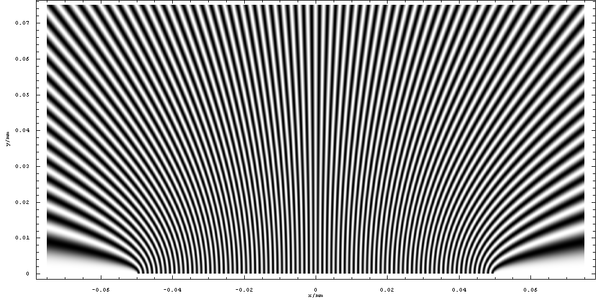
在这个尺度上，条纹结构不是明显径向的，它围绕光源“弯曲”。但是，我们可以看到，如果我们放大，条纹会发散，而中心附近的条纹（最接近完全径向的条纹）将是最重要的条纹

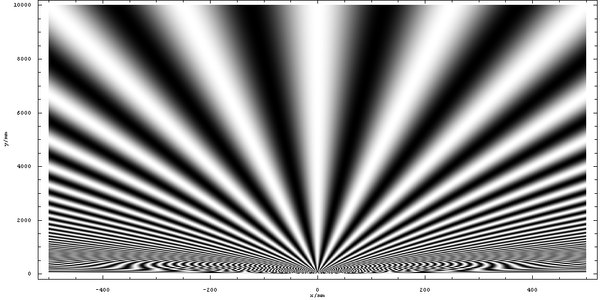
在这幅图中，我们看到了预测的亮条纹，分别位于 x=0mm、x=±250mm 和 x=±500mm 处。

宽缝隙

双宽缝实验中的路径长度差。