波/向量

波 : 二维和三维波
1 - 2 - 3 - 4 - 5 - 6 - 7
问题

数学教程 - 向量

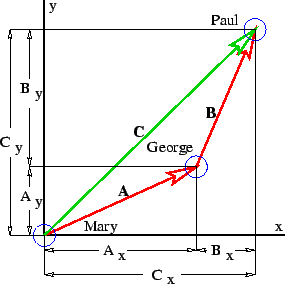
图 1: 平面中的位移向量。
向量 ${\mbox{A}}$ 代表乔治从玛丽的位移，而向量 ${\mbox{B}}$ 代表保罗从乔治的位移。向量 ${\mbox{C}}$ 代表保罗从玛丽的位移，并且 ${\mbox{C}}={\mbox{A}}+{\mbox{B}}$。量 $A_{x}$，$A_{y}$ 等，代表向量的笛卡尔坐标。

在我们继续之前，我们需要探索向量的概念。向量是一个表示大小和方向的量。在图形上，我们将向量表示为箭头。在排版符号中，向量用粗体字表示，而在手写中，在表示向量的字符上画一个箭头。

图 1 展示了一些位移向量的例子，即表示一个物体相对于另一个物体的位移的向量，并介绍了向量加法的概念。向量 ${\mbox{B}}$ 的尾部与向量 ${\mbox{A}}$ 的头部重合，连接 ${\mbox{A}}$ 尾部和 ${\mbox{B}}$ 头部的向量是 ${\mbox{A}}$ 和 ${\mbox{B}}$ 的和，在图 1 中称为 ${\mbox{C}}$。

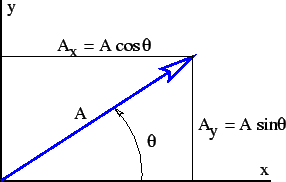
图 2: 用于表示二维向量方向的角 $\theta$ 的定义草图。

量 $A_{x}$，$A_{y}$等，代表图2中矢量的笛卡尔坐标分量。一个矢量可以用它的笛卡尔坐标分量来表示，笛卡尔坐标分量只是矢量在笛卡尔坐标轴上的投影，也可以用它的方向和大小来表示。二维矢量的方向通常用矢量相对于 $x$ 轴的逆时针角度来表示，如图2所示。从一种形式到另一种形式的转换由以下公式给出。

$A=(A_{x}^{2}+A_{y}^{2})^{1/2}\qquad \theta =\tan ^{-1}(A_{y}/A_{x}),$

$A_{x}=A\cos(\theta )\qquad A_{y}=A\sin(\theta ),$

其中 $A$ 是矢量的大小。矢量大小有时用绝对值符号表示：$A\equiv \vert {\mbox{A}}\vert$。

请注意，反正切函数给出的结果对于添加或减去 $\pi$ 的整数倍是不确定的。因此，必须通过独立检查 $A_{x}$ 和 $A_{y}$ 的符号来确定角度所在的象限，并选择 $\theta$ 的适当值。

要将两个矢量 ${\mbox{A}}$ 和 ${\mbox{B}}$ 相加，最简单的方法是将它们转换为笛卡尔坐标分量形式。然后，和 ${\mbox{C}}={\mbox{A}}+{\mbox{B}}$ 的分量只是分量的和。

$C_{x}=A_{x}+B_{x}\qquad C_{y}=A_{y}+B_{y}.$

矢量的减法类似地完成，例如，如果 ${\mbox{A}}={\mbox{C}}-{\mbox{B}}$，则

$A_{x}=C_{x}-B_{x}\qquad A_{y}=C_{y}-B_{y}.$

单位向量是一个长度为1的向量。可以通过将普通向量除以其长度来构造一个单位向量：${\mbox{n}}={\mbox{A}}/\vert {\mbox{A}}\vert$。该除法运算通过将每个向量分量除以分母中的数字来执行。或者，如果向量以长度和方向表示，则向量的幅值除以分母，方向保持不变。

单位向量可用于定义笛卡尔坐标系。按照惯例，${\mbox{i}}$，${\mbox{j}}$，和${\mbox{k}}$分别指示该系统的$x$，$y$，和$z$轴。请注意，${\mbox{i}}$，${\mbox{j}}$，和${\mbox{k}}$是相互垂直的。任何向量都可以用单位向量及其笛卡尔分量表示：${\mbox{A}}=A_{x}{\mbox{i}}+A_{y}{\mbox{j}}+A_{z}{\mbox{k}}$。表示向量的另一种方法是作为分量列表：${\mbox{A}}=(A_{x},A_{y},A_{z})$。我们倾向于使用后一种表示，因为它是一种比较简洁的符号。

有两种方法可以将两个向量相乘，分别产生称为点积和叉积的结果。叉积产生另一个向量，而点积产生一个数字。这里我们将只讨论点积。

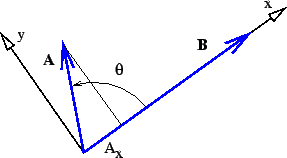图 3: 点积的定义草图。

给定向量 ${\mbox{A}}$ 和 ${\mbox{B}}$，这两个向量的点积定义为

${\mbox{A}}\cdot {\mbox{B}}\equiv \vert {\mbox{A}}\vert \vert {\mbox{B}}\vert \cos \theta ,$

其中 $\theta$ 是这两个向量之间的夹角。点积的另一种表达式用向量笛卡尔坐标表示

${\mbox{A}}\cdot {\mbox{B}}=A_{x}B_{x}+A_{y}B_{y}.$

很容易证明当 $x$ 轴沿着其中一个向量时，这与点积的余弦形式是等效的，如图 3 所示。特别要注意，$A_{x}=\vert {\mbox{A}}\vert \cos \theta$，而 $B_{x}=\vert {\mbox{B}}\vert$ 和 $B_{y}=0$。因此，${\mbox{A}}\cdot {\mbox{B}}=\vert {\mbox{A}}\vert \cos \theta \vert {\mbox{B}}\vert$，在这种情况下，这与上面给出的形式相同。

根据余弦定律，我们也可以看到

$\mathbf {A} \cdot \mathbf {B} ={\frac {1}{2}}\left(|\mathbf {A} +\mathbf {B} |^{2}-|\mathbf {A} |^{2}-|\mathbf {B} |^{2}\right)$

这是点积的另一种无坐标表达式。

图 4：旋转坐标系的定义图。向量 ${\mbox{R}}$ 在未加撇的坐标系中具有分量 $X$ 和 $Y$，在加撇的坐标系中具有分量 $X'$ 和 $Y'$。

为了使方程式 (2.6) 一般情况下成立，剩下的唯一需要证明的就是无论笛卡尔坐标系相对于向量的方向如何，它都能得出相同的结果。为此，我们必须证明 $A_{x}B_{x}+A_{y}B_{y}=A_{x}'B_{x}'+A_{y}'B_{y}'$，其中撇号表示旋转后的坐标系中的分量。

这可以通过应用勾股定理几乎立即证明。由于 R 是不变的，并且代表两个三角形（X, X', Y 和 Y'）的斜边，我们可以得出结论

$|R|^{2}=X^{2}+Y^{2}{\mbox{ and }}|R|^{2}=X'^{2}+Y'^{2}\Rightarrow X^{2}+Y^{2}=X'^{2}+Y'^{2}$

由于点积可以像上面一样仅用大小来表示，如果向量的模是不变的，那么两个向量的点积也必须是不变的。

要推导出 X' 和 Y' 的一般公式，你需要多思考一些

图 2.4 显示了向量 ${\mbox{R}}$ 在两个相互旋转的坐标系中分解。从该图可以清楚地看出 $X'=A+B$。聚焦于阴影三角形，我们可以看到 $A=X\cos \theta$ 和 $B=Y\sin \theta$。因此，我们发现 $X'=X\cos \theta +Y\sin \theta$。类似的推理表明 $Y'=-X\sin \theta +Y\cos \theta$（想象一下，在不改变轴名称的情况下，将图像中的结构再旋转 90°。你会立即注意到，在第二象限中，X 为负而 Y 为正）。

因此，新旧坐标的关系为

${\begin{pmatrix}X^{\prime }\\Y^{\prime }\end{pmatrix}}={\begin{pmatrix}X\cos \theta +Y\sin \theta \\-X\sin \theta +Y\cos \theta \end{pmatrix}}$

这对位置向量是成立的。我们可以用它来扩展向量概念，使其不仅限于位置，而是声明一对数字是向量，当且仅当它们的值在旋转下以这种方式变化。

将此关系代入我们之前点积的表达式，并使用三角恒等式 $\cos ^{2}\theta +\sin ^{2}\theta =1$，得到

${\begin{matrix}A_{x}'B_{x}'+A_{y}'B_{y}'&=&&(A_{x}\cos \theta +A_{y}\sin \theta )(B_{x}\cos \theta +B_{y}\sin \theta )\\&&+&(-A_{x}\sin \theta +A_{y}\cos \theta )(-B_{x}\sin \theta +B_{y}\cos \theta )\\&=&&A_{x}B_{x}+A_{y}B_{y}\end{matrix}}$

这证明了上面提到的两种点积形式的完全等价性。(展开上面的表达式以验证这一点。)

一个不依赖于使用哪个坐标系的数量被称为标量。两个向量的点积是一个标量。然而，单独取的向量的分量不是标量，因为分量随着坐标系的改变而改变。由于物理定律不能依赖于使用的坐标系的选择，我们坚持要求物理定律用标量和向量来表示，而不是用向量的分量来表示。

在三维空间中，点积的余弦形式保持不变，而分量形式为

${\mbox{A}}\cdot {\mbox{B}}=A_{x}B_{x}+A_{y}B_{y}+A_{z}B_{z}.$