波/衍射光栅

波 : 二维和三维波
1 - 2 - 3 - 4 - 5 - 6 - 7
问题

衍射光栅

由于双缝情况下的干涉峰的角间距 $\Delta \theta$ 取决于入射波的波长，所以双缝系统可以作为一个粗略的装置，来区分作用在缝隙上的非正弦波的不同分量的波长。但是，如果增加更多缝隙，并保持缝隙之间的均匀间距 $d$ ，我们得到一个更复杂的装置，用于区分光束分量。这被称为衍射光栅。

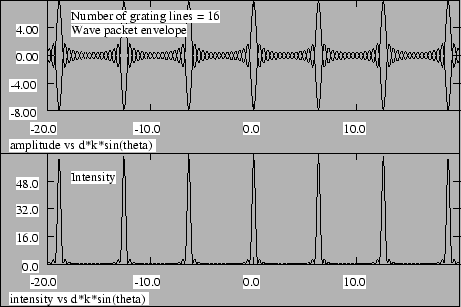
图 2.17-2.19 分别显示了 2、4 和 16 个缝隙的光栅的衍射图样的振幅和强度。请注意，干涉峰的位置保持不变，但随着缝隙数量的增加，峰值的锐度增加。

峰值的宽度实际上与光栅的总宽度有关， $w=nd$ ，其中 $n$ 是缝隙的数量。将此宽度视为一个大的单缝的尺寸，单缝方程 $\alpha _{max}=\lambda /(2w)$ ，告诉我们峰值的角宽度。

干涉峰的角宽度由单缝方程控制，而它们的角位置由双缝方程控制。为了简单起见，我们假设 $\vert \theta \vert <<1$ ，这样我们就可以对双缝方程进行小角度近似， $m\lambda =d\sin \theta \approx d\theta$ ，并提出以下问题：两个波长必须相差多少才能使两个波的干涉峰不重叠？为了使峰值可辨别，它们在 $\theta$ 上的间隔应大于每个峰值的角宽度， $\alpha _{max}$

\Delta \theta >\alpha _{max}.

(3.24)

将上述表达式代入 $\Delta \theta$ 和 $\alpha _{max}$ ，并解出 $\Delta \lambda$ ，得到 $\Delta \lambda >\lambda /(2mn)$ ，其中 $n=w/d$ 是衍射光栅中的狭缝数。因此，可由衍射光栅分辨的波长之间的分数差仅取决于干涉级数 $m$ 和光栅中的狭缝数 $n$ 。

{\frac {\Delta \lambda }{\lambda }}>{\frac {1}{2mn}}.

(3.25)

有关衍射和衍射光学的更多信息