波/平面叠加

波 : 二维和三维波
1 - 2 - 3 - 4 - 5 - 6 - 7
问题

平面波的叠加

我们现在通过询问两个平面正弦波叠加后的样子来研究二维波包。 如果这两个波具有不同的波数，但它们的波矢量指向同一个方向，则结果与前一章中介绍的结果相同，只是波包在垂直于波矢量的方向上无限延伸而不改变形状。在这种情况下产生的波包沿着波矢量的方向前进，因此对于静止的观察者来说，就像一系列宽阔横向范围的经过的脉冲。

叠加两个具有相同频率的平面波会导致一个静止的波包，单个波前通过该波包。 该波包也在某个方向上无限延伸，但延伸方向取决于所考虑波的色散关系。人们可以将这种波包视为稳定的光束，它引导某个方向的单个相位波，但它们本身不会随时间变化。通过叠加多个平面波，所有平面波都具有相同的频率，实际上可以产生一个静止的光束，就像可以通过叠加多个具有指向相同方向的波矢量的波来产生一个孤立的脉冲一样。

两个相同波长的波

如果波的频率取决于波矢量的大小，但不取决于它的方向，则该波的色散关系称为各向同性。 在各向同性的情况下，只有当两个波的波矢量长度，因此它们的波长相同，两个波的频率才相同。 图 2.6 中的前两个示例满足此条件。在本节中，我们研究由叠加的各向同性波产生的光束。

我们叠加两个平面波，其波矢量分别为${\mbox{k}}_{1}=(-\Delta k_{x},k_{y})$ 和 ${\mbox{k}}_{2}=(\Delta k_{x},k_{y})$。两种情况下的波矢量长度均为 $k_{1}=k_{2}=(\Delta k_{x}^{2}+k_{y}^{2})^{1/2}$

$A=\sin(-\Delta k_{x}x+k_{y}y-\omega t)+\sin(\Delta k_{x}x+k_{y}y-\omega t).$ (3.15)

如果 $\Delta k_{x}<<k_{y}$，则两个波都近似地在 $y$ 方向移动。这种波的一个例子是两个具有相同频率但以略微不同的方向移动的光波。

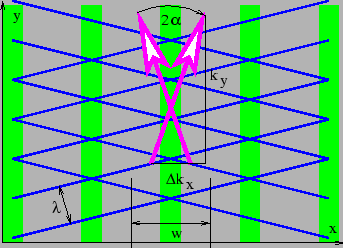图 2.7：两个具有相同波长但以不同方向定向的平面波的波前和波矢量。 垂直条带显示了波前重合的干涉相长区域。条带之间的垂直区域发生了干涉相消，因此定义了叠加产生的光束的横向边界。波矢量的一个分量$\Delta k_{x}$ 和 $k_{y}$ 如图所示。

应用两个角度之和的正弦的三角恒等式（正如我们之前所做的那样），方程式 (3.15) 可以简化为

$A=2\sin(k_{y}y-\omega t)\cos(\Delta k_{x}x).$ (3.16)

这是一种在$y$方向上以相速度$c_{phase}=\omega /k_{y}$和波数$k_{y}$传播的正弦波形式，在$x$方向上被余弦函数调制。$x$方向上破坏性干涉区域之间的距离$w$告诉我们所产生光束的宽度，它由$\Delta k_{x}w=\pi$给出，因此

$w=\pi /\Delta k_{x}.$ (3.17)

因此，$\Delta k_{x}$越小，光束直径越大。这种行为在图 2.7 中得到了说明。

图 2.8：两个相同波长但传播方向不同的平面波产生的光束示例。这两个波的波矢为${\mbox{k}}=(\pm 0.1,1.0)$。正位移区域用垂直阴影线表示，负位移区域用水平阴影线表示。

图 2.8 展示了两个相同波长的平面波叠加产生的光束示例，它们的方向与图 2.7 中所示相同。很容易证明所得到的波包的横向宽度满足公式 (2.17)。

两个不同波长的波

在图 2.6 的第三个示例中，波的频率仅取决于波矢的方向，与它的幅值无关，这与各向同性色散关系正好相反。在这种情况下，不同方向但频率相同的平面波具有相同方向但长度不同的波矢。

更一般地说，人们可能会遇到频率依赖于波矢方向和幅值的波。在这种情况下，两个不同方向但频率相同的平面波通常具有方向和幅值都不同的波矢。

图 2.9：两个不同波长且方向不同的平面波的波前和波矢。倾斜的条带显示了波前重合的相长干涉区域。条带之间的倾斜区域发生相消干涉，并且如前所述，定义了叠加产生的光束的横向极限。

数学上，我们可以将这两个波的叠加表示为公式 (2.15) 的推广

$A=\sin[-\Delta k_{x}x+(k_{y}+\Delta k_{y})y-\omega t]+\sin[\Delta k_{x}x+(k_{y}-\Delta k_{y})y-\omega t].$ (3.18)

在这个方程中，我们给出了第一个波矢的 y 方向分量 $y$ 为 $k_{y}+\Delta k_{y}$，而第二个波矢的 y 方向分量为 $k_{y}-\Delta k_{y}$。因此，第一个波的总波数为 $k_{1}=[\Delta k_{x}^{2}+(k_{y}+\Delta k_{y})^{2}]^{1/2}$，而第二个波的总波数为 $k_{2}=[\Delta k_{x}^{2}+(k_{y}-\Delta k_{y})^{2}]^{1/2}$，因此 $k_{1}\neq k_{2}$。利用常用的三角恒等式，我们将方程 (2.18) 写成：

$A=2\sin(k_{y}y-\omega t)\cos(-\Delta k_{x}x+\Delta k_{y}y).$ (3.19)

为了理解这个方程的含义，注意到当 $-\Delta k_{x}x+\Delta k_{y}y=m\pi$时，两个波之间发生相长干涉，其中 $m$ 是一个整数。解这个方程关于 $y$，得到 $y=(\Delta k_{x}/\Delta k_{y})x+m\pi /\Delta k_{y}$，对应于斜率为 $\Delta k_{x}/\Delta k_{y}$ 的直线。这些直线垂直于两个波矢的矢量差 ${\mbox{k}}_{2}-{\mbox{k}}_{1}=(2\Delta k_{x},-2\Delta k_{y})$。证明这一点最简单的方法是注意到，该差矢量的方向是使它具有斜率 $-\Delta k_{y}/\Delta k_{x}$。与相长干涉直线的斜率 $\Delta k_{x}/\Delta k_{y}$ 相比，表明了这一点。

图 2.10：两个平面波产生波束的示例，这两个平面波的波矢在方向和大小上都不同。这两个波的波矢为 ${\mbox{k}}_{1}=(-0.1,1.0)$ 和 ${\mbox{k}}_{2}=(0.1,0.9)$。正位移区域用垂直阴影线表示，负位移区域用水平阴影线表示。

图 2.10 展示了两个方向和波长不同的波叠加产生波束的示例。注意，波前仍然是水平的，如 图 2.8 所示，但波束不是垂直的，而是向右倾斜。

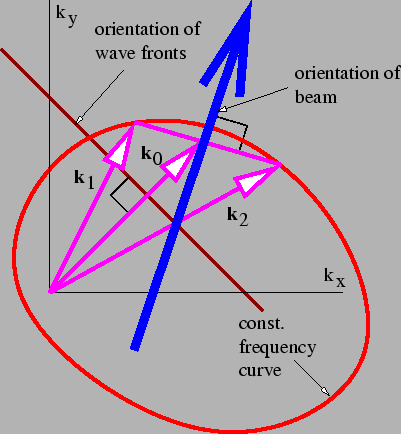图 2.11：说明了两个具有相同频率的平面波叠加时所涉及的因素。波前垂直于两个波矢的矢量平均值 ${\mbox{k}}_{0}=({\mbox{k}}_{1}+{\mbox{k}}_{2})/2$，而定义波束方向的相长干涉线垂直于这两个矢量的差值 ${\mbox{k}}_{2}-{\mbox{k}}_{1}$。

图 2.11 总结了我们对相同频率的平面波叠加的了解。一般来说，波束方向和相长干涉线不垂直于波前。这种情况只发生在波频率与波矢方向无关时。

多个具有相同波长的波

与一维波包类似，我们可以将两个以上的波叠加在一起以产生一个孤立的波包。在这里，我们将注意力集中在各向同性色散关系的情况下，其中给定频率的所有波矢都具有相同的长度。

图 2.12：说明了可以叠加在一起的平面波的波矢。

图 2.12 展示了一个示例，其中将具有相同波长但方向不同的波矢叠加在一起。定义 $\alpha _{i}$ 为第 $i$ 个波矢从垂直方向顺时针旋转的角度，如图 2.12 所示，我们可以将这些波在时间 $t=0$ 时的叠加写成 $A=\sum _{i}A_{i}\sin(k_{xi}x+k_{yi}y)$

$=\sum _{i}A_{i}\sin[kx\sin(\alpha _{i})+ky\cos(\alpha _{i})]$ (3.20)

其中我们假设 $k_{xi}=k\sin(\alpha _{i})$ 和 $k_{yi}=k\cos(\alpha _{i})$。参数 $k=\vert {\mbox{k}}\vert$ 是波矢的大小，对于所有波来说都是相同的。在这个例子中，我们还假设每个波分量的幅度随着 $\vert \alpha _{i}\vert$ 的增大而减小。

$A_{i}=\exp[-(\alpha _{i}/\alpha _{max})^{2}].$ (3.21)

指数函数随着其自变量变为负而快速下降，出于实际目的，只有波矢满足 $\vert \alpha _{i}\vert \leq \alpha _{max}$ 的波矢对总和有显著贡献。我们将 $\alpha _{max}$ 称为 *扩展角*。

图 2.13: 对于 $\alpha _{max}=0.8$ 和 $k=1$，公式 (2.20) 中的位移场 $A(x,y)$ 的图。

图 2.13 展示了当 $\alpha _{max}=0.8{\mbox{ radians}}$ 且 $k=1$ 时 $A(x,y)$ 的样子。注意，对于 $y=0$，波幅只有在 $-4<x<4$ 的小范围内才较大。然而，对于 $y>0$，波浪传播成一个宽阔的半圆形图案。

图 2.14: 对于 $\alpha _{max}=0.2$ 和 $k=1$，公式 (2.20) 中的位移场 $A(x,y)$ 的图。

图 2.14 展示了当扩展角 $\alpha _{max}=0.2{\mbox{ radians}}$ 时计算出的 $A(x,y)$ 的图案。在这种情况下，波幅在 $y=0$ 的更宽的 $x$ 范围内都很大，大约为 $-12<x<12$。另一方面，与图 2.13 相比，波浪的后续传播要小得多。

我们得出结论，具有窄波矢分布的平面波叠加，其中心波矢指向 $y$ 方向（如 2.14 图所示），会产生一个最初在 $x$ 方向上很宽，但随着 $y$ 增加其宽度只略微增加的光束。然而，具有更宽波矢分布的平面波叠加（如 2.13 图所示）会产生一个最初在 $x$ 方向上很窄，但随着 $y$ 增加其宽度迅速增加的光束。

通过与本节开头讨论的两个波叠加的结果进行比较，可以更好地理解扩展角 $\alpha _{max}$ 和光束初始宽度的关系。如公式 (2.17) 所示，较大的 $k_{x}$ 值，因此 $\alpha$，与波包在 $x$ 方向上的尺寸小有关，反之亦然。两个波的叠加没有捕捉到当许多波叠加时发生的后续光束扩散，但它确实导致了 $\alpha _{max}$（在两个波的情况下只是 $\tan ^{-1}(k_{x}/k_{y})$）和光束初始宽度的粗略定量关系。如果我们对 $\alpha =\alpha _{max}$ 使用小角度近似，使得 $\alpha _{max}=\tan ^{-1}(k_{x}/k_{y})\approx k_{x}/k_{y}\approx k_{x}/k$，那么 $k_{x}\approx k\alpha _{max}$，公式 (2.17) 可以写成 $w=\pi /k_{x}\approx \pi /(k\alpha _{max})=\lambda /(2\alpha _{max})$。因此，我们可以从波的波长 $\lambda$ 和光束的初始宽度 $w$ 找到近似扩展角。

$\alpha _{max}\approx \lambda /(2d)\quad {\mbox{(single slit spreading angle)}}.$ (3.22)