微积分/一些重要定理

本节涵盖了微分学中三个基本重要的定理：极值定理、罗尔定理和中值定理。它还讨论了可导性和连续性之间的关系。

极值定理

极值的分类

我们从一些定义开始。

全局最大值

函数$f$在闭区间$[a,b]$上的全局最大值（也称为绝对最大值）是某个值$f(c)$，使得对于所有$x\in [a,b]$，都有$f(c)\geq f(x)$。

全局最小值

函数$f$在闭区间$[a,b]$上的全局最小值（也称为绝对最小值）是某个值$f(c)$，使得对于所有$x\in [a,b]$，都有$f(c)\leq f(x)$。

最大值和最小值统称为极值。

极值定理

极值定理

如果$f$是在闭区间$[a,b]$上连续的函数，那么$f$在$[a,b]$上既有全局最小值，也有全局最大值。假设$a,b$都是有限的。

极值定理是实分析中的一个基本结果，其证明超出了本文的范围。但是，该定理的正确性使我们能够讨论闭区间上连续函数的最大值和最小值，而无需考虑它们是否存在。当处理不满足定理前提的函数时，我们需要考虑这些问题。例如，无界函数$f(x)=x$根本没有任何极值。如果$f(x)$被限制在半闭区间$[0,1)$上，则$f$在$x=0$处具有最小值0，但它没有最大值，因为对于任何给定的值$c\in [0,1)$，总能找到$f(x)$更大的值，其中$x\in [0,1)$，例如通过形成$f(d)$，其中$d$是$c$与1的平均值。函数$g(x)={\frac {1}{x}}$在$x=0$处不连续。$g(x)$在围绕$x=0$的任何闭区间内都没有任何极值，因为当从左侧接近0时函数是无界下降的，而当从右侧接近0时函数是无界上升的。（事实上，函数在$x=0$处未定义。但是，如果将$g(0)$赋值为任意值，则该示例不受影响。)

极值定理是一个存在定理。它告诉我们，如果满足某些条件，则全局极值存在，但它没有告诉我们如何找到它们。我们将在标题为极值和拐点的部分中讨论如何确定连续函数的极值。

罗尔定理

罗尔定理

如果函数$f(x)$

• 在闭区间$[a,b]$上连续
• 在开区间$(a,b)$上可导
• $f(a)=f(b)$

那么至少存在一个数$c\in (a,b)$，使得

$f'(c)=0$

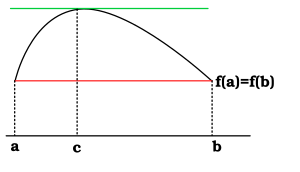
罗尔定理在证明均值定理中非常重要。直观地说，它表示如果有一个函数在区间内处处连续，并且该区间的边界点处的函数值相同，并且如果该函数在区间内处处可导（除了可能在端点处），那么该函数在区间内部至少存在一个地方斜率为零。

罗尔定理的证明

如果$f$在$[a,b]$上是常数，则对于每个$x\in [a,b]$，$f'(x)=0$，因此定理成立。因此，在接下来的讨论中，我们假设$f$在$[a,b]$上不是常数。

由于$f$满足极值定理的条件，$f$必须在$[a,b]$上取得其最大值和最小值。由于$f$在$[a,b]$上不是常数，端点不可能同时是最大值和最小值。因此，至少存在一个极值在$(a,b)$内。我们可以假设，不失一般性，这个极值是一个最大值，因为如果它是一个最小值，我们可以考虑函数$-f$。令$f(c)$，其中$c\in (a,b)$为最大值。剩下的需要证明的是$f'(c)=0$。

根据导数的定义，$f'(c)=\lim _{h\to 0}{\frac {f(c+h)-f(c)}{h}}$。将$h=x-c$代入，这等价于$\lim _{x\to c}{\frac {f(x)-f(c)}{x-c}}$。注意，对于所有$x\in [a,b]$，$f(x)-f(c)\leq 0$，因为$f(c)$是$[a,b]$上的最大值。

$\lim _{x\to c^{-}}{\frac {f(x)-f(c)}{x-c}}\geq 0$，因为分子非正，分母为负。

$\lim _{x\to c^{+}}{\frac {f(x)-f(c)}{x-c}}\leq 0$，因为分子非正，分母为正。

由于函数在$c$处可导，因此左右极限必须相等，所以$\lim _{x\to c}{\frac {f(x)-f(c)}{x-c}}=0=f'(c)$。

练习

1. 证明罗尔定理适用于函数$f(x)=x^{2}-3x$的x截距之间。

均值定理

均值定理

如果函数$f(x)$

• 在闭区间$[a,b]$上连续
• 在开区间$(a,b)$上可导

则存在至少一个$c\in (a,b)$ 使得

$f'(c)={\frac {f(b)-f(a)}{b-a}}$

均值定理是微积分中的一个重要定理。它基本上说，对于定义在区间上的可微函数，区间上存在某个点的瞬时斜率等于该区间的平均斜率。请注意，当$f(a)=f(b)$ 时，罗尔定理是均值定理的特例。

为了证明均值定理，我们将证明一个更一般的陈述，均值定理是其特例。该陈述是柯西均值定理，也称为扩展均值定理。

柯西均值定理

柯西均值定理

如果$f(x),g(x)$ 是

• 在闭区间$[a,b]$上连续
• 在开区间$(a,b)$上可导

则存在一个数$c\in (a,b)$ 使得

$f'(c)(g(b)-g(a))=g'(c)(f(b)-f(a))$

如果$g(b)\neq g(a)$ 且$g'(c)\neq 0$ ，则这等价于

${\frac {f'(c)}{g'(c)}}={\frac {f(b)-f(a)}{g(b)-g(a)}}$

为了证明柯西中值定理，考虑函数

$h(x)=f(x)(g(b)-g(a))-g(x)(f(b)-f(a))-f(a)g(b)+f(b)g(a)$

由于 $f$ 和 $g$ 在 $[a,b]$ 上连续并在 $(a,b)$ 上可微，因此 $h$ 也是如此。

$h'(x)=f'(x)(g(b)-g(a))-g'(x)(f(b)-f(a))$

由于 $h(a)=h(b)$（参见练习），罗尔定理告诉我们存在某个数 $c\in (a,b)$ 使得 $h'(c)=0$。这意味着

$f'(c)(g(b)-g(a))=g'(c)(f(b)-f(a))$

这就是需要证明的。

练习

2. 证明 $h(a)=h(b)$，其中 $h(x)$ 是在柯西中值定理证明中定义的函数。

3. 证明均值定理可由柯西均值定理推导得出。

4. 求满足函数$f(x)=x^{3}$在端点$x=0$和$x=2$的区间上的平均值定理的$x=c$。

5. 求满足函数$f(x)=\sin(x)$以及区间$[0,\pi ]$上的平均值定理的点。

可导蕴含连续

如果$f'(x_{0})$存在，则$f$在$x_{0}$处连续。要看到这一点，请注意$\lim _{x\to x_{0}}(x-x_{0})f'(x_{0})=0$。但是

${\begin{aligned}\lim _{x\to x_{0}}(x-x_{0})f'(x_{0})&=\lim _{x\to x_{0}}(x-x_{0}){\frac {f(x)-f(x_{0})}{x-x_{0}}}\\&=\lim _{x\to x_{0}}(f(x)-f(x_{0}))\\&=\lim _{x\to x_{0}}f(x)-f(x_{0})\end{aligned}}$

这意味着$\lim _{x\to x_{0}}f(x)-f(x_{0})=0$ 或 $\lim _{x\to x_{0}}f(x)=f(x_{0})$，这表明$f$ 在 $x=x_{0}$ 处是连续的。

然而，反之则不成立。例如，取 $f(x)=|x|$。 $f$ 在 0 处是连续的，因为 $\lim _{x\to 0^{-}}|x|=\lim _{x\to 0^{-}}-x=0$ 且 $\lim _{x\to 0^{+}}|x|=\lim _{x\to 0^{+}}x=0$，且 $|0|=0$，但它在 0 处不可导，因为 $\lim _{h\to 0^{-}}{\frac {|0+h|-|0|}{h}}=\lim _{h\to 0^{-}}{\frac {-h}{h}}=-1$，但 $\lim _{h\to 0^{+}}{\frac {|0+h|-|0|}{h}}=\lim _{h\to 0^{+}}{\frac {h}{h}}=1$。