待办事项	编辑说明本书仍在开发中。请帮助我们

参数外部射线^[1]^[2]

调整外部射线

杜瓦迪的魔法公式^[3]：克劳德： “杜瓦迪的魔法公式通过在二进制展开式前加 10 或 01（取决于角度是否低于或高于 1/2）来将心形线上的射线映射到实轴。这篇论文涉及静脉和哈伯德树” ^[4]

着陆

对于具有有界后临界集的复多项式 f，杜瓦迪-哈伯德着陆定理针对周期性外部

每个周期性外部射线都着陆在一个排斥或抛物线周期点上
相反，每个排斥或抛物线点都是至少一个周期性外部射线的着陆点

问答

参数与动态射线之间的关系

尾流

曼德布罗集演示 3（外部射线）第 8 页

对于 p 周期角，连接的朱利亚集的相应动态射线着陆在一个周期除以 p 的排斥或抛物线点上。相应的参数射线着陆在一个周期为 p 的双曲分量的根部。

为了证明这一点，考虑一个参数 c0，其中参数射线累积。对于此射线上的参数 c，相应的动态射线分支。如果 c0 的动态射线着陆在一个排斥周期点上，那么根据隐函数定理和拉回参数，它也会在 c ≈ c0 时不着陆。这个矛盾表明 c0 的动态射线必须着陆在一个抛物线点上，而 c0 则是一个根。

事实上，恰好有两个具有周期角的参数射线着陆在每个根部。这由

阿德里安·杜瓦迪和约翰·哈马尔·哈伯德使用抛物线内爆的 Fatou 坐标（第 2 章）证明。
迪尔克·施莱希特和约翰·米尔诺提供了组合证明。

对于位于两条参数射线之间的尾流中的参数 c

具有相同角度的两条动态射线一起着陆，
临界值 z = c 始终位于它们之间的尾流中，即使还有更多动态射线着陆。

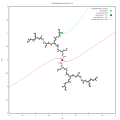
左侧图像显示了具有 2 周期角 1/3 和 2/3 的参数射线，它们着陆在周期为 2 的分量的根部。十字表示中心 c = -1。

右侧图像显示了相应的填充朱利亚集（“大教堂”）以及着陆在排斥不动点 αc 上的两条动态射线。十字表示临界值 z = c。现在，您将看到对应于 p 周期角 1/(2p-1) 和 2/(2p-1) 的中心的朱利亚集，以及所有具有这些分母的参数射线：按回车键或按“Go”按钮以增加周期（2...9）。

细分规则

如何计算着陆在临界点 $z=0$ 的树枝状朱利亚集的动态外部射线？

步骤

前周期角 $\theta$ （具有偶数分母的十进制小数）
在参数平面上找到参数外部射线 $\theta$ 的着陆点，它是一个米西乌列维奇点： $\gamma _{M}(\theta )=c=M$
在动态平面上
- 具有角度 $\theta$ 的射线的着陆点是临界值： $z=c$
- 在临界点 z = 0 上，着陆射线具有角度： $\theta /2$ 和 $(\theta +1)/2$

参数射线的示例：^[5]

角度为 ${\frac {1}{2}}=0.0(1)$ 的射线落到点 $c=\gamma _{M}(1/2)=-2=M_{1,1}$ ，来自参数平面。它是主天线的顶端（1/2 肢的末端）。
角度为 ${\frac {1}{4}}=0.00(1)$ 的射线落到点 $c=\gamma _{M}(1/4)=-0.228155493653962+1.115142508039937i=M_{2,1}$ ，来自参数平面。它是 1/3 尾迹的第一个顶端。
角度为 ${\frac {1}{6}}=0.0(01)$ 的射线落到点 $c=\gamma _{M}(1/6)=i=M_{1,2}$ ，来自参数平面。它是 1/3 尾迹的最后一个顶端
角度为 ${\frac {17}{240}}=0001(0010)$ 的射线落到点 $c=\gamma _{M}(17/240)=0.366362983422764+0.591533773261445i=M_{4,4}$ ，来自参数平面。它是 1/4 尾迹的主 Misiurewicz 点（分支点或枢纽）。
角度为 ${\frac {9}{56}}=0.001(010)$ 的射线落到点 $c=\gamma _{M}(9/56)=-0.101096363845622+0.956286510809142i=M_{3,3}$ ，来自参数平面。它是 1/3 尾迹的主 Misiurewicz 点（分支点或枢纽）。
角度为 ${\frac {129}{16256}}=0.0000001(0000010)$ 的射线落在参数平面的点 $c=\gamma _{M}(129/16256)=0.397391822296541+0.133511204871878i=M_{7,7}$ 上。它就是 1/7 区域的主Misiurewicz点（分支点或中心点）。

动态平面上由动态射线划分的动态平面分区与 kneading 序列有关。

1/4
1/6
9/56
129/16256

主Misiurewicz点规则

来自 Wolf Jung 编写的程序 mandel演示 3（外部射线）第 9/12 页的笔记

角度为 1/7 和 2/7 的参数射线落在周期为 3 的分量根部，该分量是旋转数为 1/3 的卫星型分量。

对于区域中所有射线之间的参数 c

对于 Mandelbrot 集 1/3 肢体中的 c
- 对于等于区域的主Misiurewicz点的 c

角度为 1/7、2/7 和 4/7 的动态射线

共同落在排斥不动点 $z=\alpha _{c}$ 上。
临界值 z = c 位于前两条射线之间。

我们将计算不动点 alpha $z=\alpha _{c}$ 在 $f_{c}(z)$ 下的某些原像的外部角。

注意，角度 $\theta$ 在模 1 倍增下的两个原像是 $(\theta /2,(\theta +1)/2)$ 。

点 $z=-\alpha _{c}$ 是 $z=\alpha _{c}$ 唯一的原像，与不动点本身不同。

角度 1/7 的原像是 (1/7)/2 = 1/14 和 (1/7 + 1)/2 = 4/7。后一个角度属于 $z=\alpha _{c}$ ，所以 1/14 是 $z=-\alpha _{c}$ 的外部角。

同样，可以得到其他角度 9/14 和 11/14。这些射线用蓝色绘制。

将 z 移动到 2/7 和 4/7 射线之间 $z=-\alpha _{c}$ 的原像。角度 1/14 的原像是 (1/14)/2 = 1/28 和 (1/14 + 1)/2 = 15/28。只有后一个角度在选定区间内。z 的另外两个外部角度是 9/28 和 11/28。这些射线用洋红色绘制。

现在 z 是 1/7 和 2/7 射线之间原像。通过在该区间内取原像，可以得到外部角度 9/56、11/56 和 15/56。这些射线用红色绘制。

具有前周期角度（即，偶数分母）的射线落在动态平面的前周期点上，或者落在参数平面的 Misiurewicz 点上。对于这些参数，临界值在 fc(z) 的迭代下是前周期的。

排斥不动点 alpha $z=\alpha _{c}$ 的轨道周期为 3
z	轨道肖像	描述
-0.327586178699357 +0.577756453298949 i	(1/7, 2/7, 4/7)	排斥不动点 α $z=\alpha _{c}$
+0.327586178699356 -0.577756453298949 i	(1/14, 9/14, 11/14)	原像: $z=b(\alpha _{c})=f^{-1}(\alpha _{c})=-\alpha _{c}$
-1.005359779818338 +0.762932332734299 i	(9/28, 11/28, 15/28 )	a(z)
-0.101096363845622 +0.956286510809142 i	(9/56, 11/56, 和 15/56)	a(z)
-0.000000003174826 +0.000000002063599 i	(9/56, 11/56, 和 15/56)	a(z)；它应该是临界点 z = 0
-0.728941649258717 +0.655941740822478 i		a(z)
-0.184581740009785 +0.813582020547489 i		a(z)
-0.202294024682997 +0.352715534938011 i		a(z)
-0.505370243253601 +0.597157217578291 i		a(z)
-0.261224737974777 +0.687395259758146 i		a(z)
-0.276433581450372 +0.486357789166200 i		a(z)

符号动力学

二次多项式的符号动力学。2011 年 7 月 27 日版。Henk Bruin、Alexandra Kaffl 和 Dierk Schleicher
- 长版本
- 短版本

想法

取一条直射线段（接近无穷大）
将其拉回曼德布罗集的边界

如何近似外部射线？

用于 Julia 集的二进制分解方法 (BDM/J)
场线标量场（势）
SAM = 条带平均方法基本上是计算角度的一种廉价方法。

BDM，一些射线可以被看到
BDM 的边界
场线
SAM

在 BDM 图像中，角度（以圈数测量）的外部射线

$angle=(k/2^{n})~~{\mbox{mod }}~1\,$

可以看作是子集的边界。

绘制外部射线意味着什么？

这意味着

计算（近似）射线的 DS 点。结果是一组复数 $\{c_{m}:1\leq m\leq DS\}$ （参数平面上的点），使用数值算法
用线段连接点，^[6] 使用图形算法）

这将给出射线 ${\mathcal {R}}$ 的近似值。

追踪以圈数为单位的角度 t 的外部射线，这意味着（Claude Heiland-Allen 的描述）^[7]

从一个大圆开始（例如 r = 65536，x = r cos(2 pi t)，y = r sin(2 pi t)）
沿着逃逸线（就像二进制分解着色的大逃逸半径的边缘）向曼德布罗集移动。

该算法为 O(周期^2)，这意味着周期加倍需要 4 倍的时间，因此它只适用于周期不超过几千的周期。

如何计算射线上的一个点？

通过求解多项式方程

   $P_{m}(c)=0$

使用数值方法。上述方程的根是点 $c_{m}$ .

  $c_{m}=c:P_{m}(c)=0$

它是外部参数射线 ${\mathcal {R}}(\theta )$ 上的一个点

  $\arg(\Phi _{M}(c_{m}))=\theta$

或

  $c_{m}\in {\mathcal {R}}(\theta )$

使用牛顿方法（迭代）可以计算点 $c_{m}$ 的近似值

你需要什么来开始？

任意选择的外角 $\theta$ ，即要绘制的射线 $R(\theta )$ 的角度。角度通常以圈数表示。
函数 P（近似于 Boettcher 映射）的值及其导数 P'
起点 $c_{m,0}$ （初始近似值）
停止规则（停止迭代的标准）：射线追踪有一个自然的停止条件：当射线进入周期为 p 的原子域时，牛顿法很可能收敛到其中心的核。^[8]

射线何时着陆 ?

"射线越来越靠近边界，但在有限时间内不会到达边界 - 对于更精确的边界点，当射线足够靠近时，你需要切换到其他方法。对于双曲分量的边界上的点，将内部角度地址（可从角度计算）拆分为岛屿和子路径分量，当追踪射线到父岛屿时，使用原子域测试（查看牛顿法是否可能收敛到正确的位置），并切换到牛顿法来找到父岛屿的核，然后通过连接分量的链追踪内部射线到所需的边界点。

对于 Misiurewicz 点，可能存在与原子域测试类似的测试，在此测试之后牛顿法将收敛到所需位置（尽管 Misiurewicz 点的射线往往比双曲分量根的射线收敛得快得多）。原子域测试检查|z|的最后一个最小值的迭代次数是否与射线的周期相同。" Claude Heiland-Allen^[9]

因此，射线在有限时间内不会"着陆"。着陆点可以表示为 $c_{\infty }$

算法

Jungreis-Ewing-Schober（JES）算法（基于 $\Phi _{M}^{-1}\,$ 在无穷远处关于 Laurent 级数的展开）
OTIS 方法（基于牛顿法）^[10]^[11]

追踪射线

向外："形式为 2pi*n/32 的外部射线，叠加在势梯度的模量上。对于每个点 c，创建一个路径来跟随势梯度的方向。每个步长与到 M 的距离估计成正比。当点足够远离 M 时，它的相位近似于 phi(c) 的相位。" Inigo Quilez^[12]
向内："绘制方法 : ... 路径以相反顺序跟随：从无穷大到 M，跟随负梯度。"

追踪射线

向内 = 从无穷大到 Mandelbrot 集
向外 = 从 Mandelbrot 集附近的点到无穷大

在穿过驻留带（水平集的边界）时收集外部角度的二进制展开的位

向内：在二进制展开的末尾添加位
向外：在二进制展开的开头添加位

穿过驻留带（水平集的边界）

当射线值改变其整数部分时

另请参阅

二进制分解
- 参数平面
- 动态平面
从二进制分解中读取位 = 收集外部角度的二进制展开的位

在

当向内追踪时，每次射线穿过驻留带（归一化迭代计数的整数部分增加 1），都会剥离最高有效位（也称为角度加倍）。

追踪角度为 t（以圈数表示）的外部射线，这意味着（Claude Heiland-Allen 的描述）^[13]

从一个大圆开始（例如 r = 65536，x = r cos(2 pi t)，y = r sin(2 pi t)）
沿着逃逸线（就像二进制分解着色的大逃逸半径的边缘）向曼德布罗集移动。

该算法为 O(周期^2)，这意味着周期加倍需要 4 倍的时间，因此它只适用于周期不超过几千的周期。

向外

 "you need to trace a ray outwards, which means using different C values, and the bits come in reverse order, first the deepest bit from the iteration count of the start pixel, then move C outwards along the ray (perhaps using the newton's method of mandel-exray.pdf in reverse), repeat until no more bits left.  you move C a fractional iteration count each time, and collect bits when crossing integer dwell boundaries" Claude Heiland-Allen

牛顿法

使用牛顿法
Tomoki Kawahira 的描述^[14]
向内追踪（从无穷大到 Mandelbrot 集）= 射线-入
任意精度（mpfr），Claude Heiland-Allen 使用动态精度调整

变量

r = 半径参数 = 半径（参见复势）
m = 半径索引 = 射线上点的索引，整数
j = 锐度 = 驻留带上的点数，整数
k = 整数深度 = 驻留带的数量，整数
d = m/S = 真实深度，浮点数（Kawahira 未使用 d 这个名称）
l = 牛顿迭代的索引（Kawahira 未使用 l 这个名称）
n = 计算牛顿映射的迭代索引

名称来自 T Kawahira 的描述

半径参数 r

常数值

S = $j_{max}$ =
D = $k_{max}$ =
R = ER = 逃逸半径
DS = $m_{max}$ = 点的数量
$L=L_{m}=l_{m,max}$

范围

清晰度 : $1\leq j\leq S$
径向索引 : $1\leq m\leq DS$
深度
- $1\leq k\leq D$
- $1\leq d\leq D$
射线的半径（子集）： $R^{1/2^{D}}\leq r<R$
迭代次数
- 二次方 : $1\leq n\leq k$
- 牛顿 : $1\leq l_{m}\leq L_{m}$

序列

m-序列（沿着射线朝向曼德勃罗集）

$r_{1},r_{2},\cdots ,r_{SD}$
$t_{1},t_{2},\cdots ,t_{SD}$
$c_{1},c_{2},\cdots ,c_{SD}$

牛顿序列 = l-序列，这里 m 是常数

从初始值 $c_{m,0}$ 朝向对 $c_{m,L}$ 的近似值
$c_{m,0},c_{m,1},\cdots ,c_{m,L}$

   $c_{m,0}{\xrightarrow {N}}c_{m,1}{\xrightarrow {N}}c_{m,1}{\xrightarrow {N}}\cdots {\xrightarrow {N}}c_{m,L}$

映射

r 映射

  $r_{m}=R^{1/2^{d}}$

将它与 c=0 动态平面上的逆迭代比较

深度

使用固定整数 D（最大深度）：^[15]

$k_{max}=D>1$

和固定的径向参数最大值（逃逸半径 = ER）

$r_{max}=R>1$

可以使用公式计算 D 个射线点

$r=R^{1/2^{k}}$

即

$1<R^{1/2^{D}}<=r<=R$

当 $k\to k_{max}=D\$ 则 $r\to 1$ 并且半径足够接近曼德勃罗集的边界

/*
Maxima CAS code

Number of ray points = depth  
r = radial parametr : 1 < R^{1/{2^D}} <= r > ER  
*/

GiveRadius( depth):=
block (
 [ r, R: 65536],
 r:R,
 print("r = ER = ", float(R)),

 for k:1   thru depth  do
   (
     r:er^(1/(2^k)),
     print("k = ", k, " r = ", float(r))
    )
)$

compile(all)$

/* --------------------------- */

GiveRadius(10)$

输出

r = ER =  65536.0 
"k = "1"  r = "256.0
"k = "2"  r = "16.0
"k = "3"  r = "4.0
"k = "4"  r = "2.0
"k = "5"  r = "1.414213562373095
"k = "6"  r = "1.189207115002721
"k = "7"  r = "1.090507732665258
"k = "8"  r = "1.044273782427414
"k = "9"  r = "1.021897148654117
"k = "10" r = "1.0108892860517

深度和锐度

如何使射线更平滑？在等值线之间添加更多点。

使用

固定整数 S = 最大锐度
固定整数 D = 最大深度

  $S>0$

可以使用公式计算 S*D 个射线点

  $m=m_{S}(j,k)=(k-1)S+j$ 
  $d=d_{S}(j,k)=d_{S}(m)={\frac {m}{S}}=(k-1)+{\frac {j}{S}}$

注意，k 等于 d 的整数部分

  $k=int(d)$

最后一个点与深度方法中相同

   $r_{d_{max}}=r_{k_{max}}$

但这里有更多点，因为

  $S*D>D$

/* Maxima CAS code */
kill(all);
remvalue(all);

GiveRadius(  depth, sharpness):=
block (
 [ r, R: 65536, d ],
 
 r:R,
 
 print("r = ER = ", float(R)),

 for k:1   thru depth  do
   (
     for j:1   thru sharpness  do
      (  d: (k-1) + j/sharpness,
         r:R^(1/(2^d)),
         print("k = ", k, " ; j = ", j , "; d = ", float(d), "; r = ", float(r))
      )
    )
)$

compile(all)$

/* --------------------------- */

GiveRadius( 10, 4)$
compile(all)$

输出

r = ER =  65536.0 
k =  1  ; j =  1 ; d =  0.25 ; r =  11224.33726645605 
k =  1  ; j =  2 ; d =  0.5 ; r =  2545.456152628088 
k =  1  ; j =  3 ; d =  0.75 ; r =  730.9641900482128 
k =  1  ; j =  4 ; d =  1.0 ; r =  256.0 
k =  2  ; j =  1 ; d =  1.25 ; r =  105.9449728229521 
k =  2  ; j =  2 ; d =  1.5 ; r =  50.45251383854013 
k =  2  ; j =  3 ; d =  1.75 ; r =  27.0363494216252 
k =  2  ; j =  4 ; d =  2.0 ; r =  16.0 
k =  3  ; j =  1 ; d =  2.25 ; r =  10.29295743812011 
k =  3  ; j =  2 ; d =  2.5 ; r =  7.10299330131601 
k =  3  ; j =  3 ; d =  2.75 ; r =  5.199648971000369 
k =  3  ; j =  4 ; d =  3.0 ; r =  4.0 
k =  4  ; j =  1 ; d =  3.25 ; r =  3.208263928999625 
k =  4  ; j =  2 ; d =  3.5 ; r =  2.665144142690224 
k =  4  ; j =  3 ; d =  3.75 ; r =  2.280273880699502 
k =  4  ; j =  4 ; d =  4.0 ; r =  2.0 
k =  5  ; j =  1 ; d =  4.25 ; r =  1.791162731021284 
k =  5  ; j =  2 ; d =  4.5 ; r =  1.632526919438152 
k =  5  ; j =  3 ; d =  4.75 ; r =  1.51005757529291 
k =  5  ; j =  4 ; d =  5.0 ; r =  1.414213562373095 
k =  6  ; j =  1 ; d =  5.25 ; r =  1.338343278468302 
k =  6  ; j =  2 ; d =  5.5 ; r =  1.277703768264832 
k =  6  ; j =  3 ; d =  5.75 ; r =  1.228843999575581 
k =  6  ; j =  4 ; d =  6.0 ; r =  1.189207115002721 
k =  7  ; j =  1 ; d =  6.25 ; r =  1.156867874248526 
k =  7  ; j =  2 ; d =  6.5 ; r =  1.13035559372475 
k =  7  ; j =  3 ; d =  6.75 ; r =  1.108532362890494 
k =  7  ; j =  4 ; d =  7.0 ; r =  1.090507732665258 
k =  8  ; j =  1 ; d =  7.25 ; r =  1.075577925697867 
k =  8  ; j =  2 ; d =  7.5 ; r =  1.063181825335982 
k =  8  ; j =  3 ; d =  7.75 ; r =  1.052868635153737 
k =  8  ; j =  4 ; d =  8.0 ; r =  1.044273782427414 
k =  9  ; j =  1 ; d =  8.25 ; r =  1.037100730738276 
k =  9  ; j =  2 ; d =  8.5 ; r =  1.031107087230023 
k =  9  ; j =  3 ; d =  8.75 ; r =  1.026093872486205 
k =  9  ; j =  4 ; d =  9.0 ; r =  1.021897148654117 
k =  10  ; j =  1 ; d =  9.25 ; r =  1.018381426940945 
k =  10  ; j =  2 ; d =  9.5 ; r =  1.015434432757735 
k =  10  ; j =  3 ; d =  9.75 ; r =  1.012962917626408 
k =  10  ; j =  4 ; d =  10.0 ; r =  1.0108892860517

m

可以使用一个循环：m 循环，并从 m 中计算 j、k 和 d

/* Maxima CAS code */
kill(all);
remvalue(all)$

GiveRadius( depth, sharpness):=
block (
 [ r, R: 65536, j, k, d, mMax ],
 
 r:float(R),
 mMax:depth*sharpness,
 
 print("r = ER = ", r),
 print( "m k j  r"),

 for m:1   thru mMax  do
   (
      d: m/sharpness,
      r:float(R^(1/(2^d))),

      k: floor(d),
      j: m - k*sharpness ,

      print( m, k, j, r)
     
    )
)$

compile(all)$

/* --------------------------- */

GiveRadius( 10, 4)$

输出

r = ER =  65536.0 
m k j r 
1 0 1 11224.33726645605 
2 0 2 2545.456152628088 
3 0 3 730.9641900482128 
4 1 0 256.0 
5 1 1 105.9449728229521 
6 1 2 50.45251383854013 
7 1 3 27.0363494216252 
8 2 0 16.0 
9 2 1 10.29295743812011 
10 2 2 7.10299330131601 
11 2 3 5.199648971000369 
12 3 0 4.0 
13 3 1 3.208263928999625 
14 3 2 2.665144142690224 
15 3 3 2.280273880699502 
16 4 0 2.0 
17 4 1 1.791162731021284 
18 4 2 1.632526919438152 
19 4 3 1.51005757529291 
20 5 0 1.414213562373095 
21 5 1 1.338343278468302 
22 5 2 1.277703768264832 
23 5 3 1.228843999575581 
24 6 0 1.189207115002721 
25 6 1 1.156867874248526 
26 6 2 1.13035559372475 
27 6 3 1.108532362890494 
28 7 0 1.090507732665258 
29 7 1 1.075577925697867 
30 7 2 1.063181825335982 
31 7 3 1.052868635153737 
32 8 0 1.044273782427414 
33 8 1 1.037100730738276 
34 8 2 1.031107087230023 
35 8 3 1.026093872486205 
36 9 0 1.021897148654117 
37 9 1 1.018381426940945 
38 9 2 1.015434432757735 
39 9 3 1.012962917626408 
40 10 0 1.0108892860517

多项式映射 q

复二次多项式

  $q_{c}(z)=z^{2}+c$

迭代

  $q_{c}^{n}(z)={q_{c}^{n-1}(z)}^{2}+c$

映射 t

    $t_{m}=t_{m}(r,\theta ):=r_{m}^{2^{k}}e^{2\pi i2^{k}\theta }$

与 c=0 平面上的正向迭代进行比较

  $z=r_{m}e^{2\pi i\theta }$

  $q_{0}^{k}(z_{m})$

多项式映射 P

P 是关于变量 c 的 $2^{k}$ 次多项式。

  $P_{m}(c):=q_{c}^{k}(c)-t_{m}$

关于 c 的导数

  $P'_{m}(c):={\frac {dP_{m}(c)}{dc}}=2P'_{m-1}(c)P_{k-m}(c)+1$

牛顿映射 N

牛顿映射:

  $N_{m}(c_{l})=c_{l}-{\frac {P_{m}(c_{l})}{P'_{m}(c_{l})}}$

注意这里

   $c_{l}=c_{m,l}$

如何计算新值 $c_{m,l+1}$ ？

从 $c_{m,l}$ 开始
计算值 $t_{m}$ （无需迭代）
计算 $C_{n}$ 和 $D_{n}$ 使用从 n=1 到 n=k 的二次迭代
使用一次牛顿迭代计算下一个点 $c_{m,l+1}$

任意名称

   $C_{n}:=q^{n}(c_{m,l})$  
   $D_{n}:=P'_{n}(c_{m,l})=(q^{n}(c_{m,l})-t)'=(q^{n}(c_{m,l}))'$

请注意常数的导数为零。

递归公式和初始值

  $C_{n}=C_{n-1}^{2}+c_{m,l};\qquad \qquad C_{1}=c_{m,l}$  
  $D_{n}=2C_{n-1}D_{n-1}+1;\qquad D_{1}=1$

在 k 次二次迭代之后，使用一次牛顿迭代计算新的值 $c_{m,l+1}$

  $c_{m,l+1}=N_{m}(c_{m,l})=c_{m,l}-{\frac {C_{k}-t_{m}}{D_{k}}}$

它在以下地方实现

mandelbrot-numerics 库
- c/lib/m_d_exray_in_step = 双精度
- c/lib/m_r_exray_in.c = mpfr（任意精度）

牛顿迭代

公式

  $c_{m,l+1}:=N(c_{m,l})$

牛顿迭代给出牛顿序列（= l 序列，这里 m 是常数）

从初始值 $c_{m,0}$ 向 $c_{m,L}$ 的近似值逼近
$c_{m,0},c_{m,1},\cdots ,c_{m,L}$

序列

   $c_{m,0}{\xrightarrow {N}}c_{m,1}{\xrightarrow {N}}c_{m,1}{\xrightarrow {N}}\cdots {\xrightarrow {N}}c_{m,L}$

初始点

$c_{1,0}=Re^{2\pi i\theta }$
值 $c_{m-1,L}$ 据推测是 $c_{m,L}$ 在射线上的“邻居”，所以将其用作 $c_{m}$ 的初始值，即 $c_{m,0}$

   $c_{m,0}=c_{m-1,L}$

代码

Claude Heiland-Allen 编写的 c 代码
- 书中的控制台程序和 GUI 版本，使用流
- mandelbrot-numerics 库
- mandelbrot 扰动器 GUI 程序
newtonRay - 来自 Wolf Jung 编写的程序 Mandel 的 cpp 代码
sage
由 Nils Berglund 制作的 Mandelbrot 电容器和场线和 c 代码：heat.c

c 代码

mpfr

使用基于 Claude Heiland-Allen 的 mandelbrot-book 代码的牛顿方法计算外部射线向内的代码

外部角度从字符串（二进制分数）中读取

/*

code is from : 
https://code.mathr.co.uk/mandelbrot-book
mandelbrot-book/code/examples/ray-in.sh
mandelbrot-book/code/examples/ray-in.c
mandelbrot-book/code/bin/mandelbrot_external_ray_in.c
mandelbrot-book/code/lib/mandelbrot_external_ray_in.c
mandelbrot-book/code/lib/mandelbrot_external_ray_in.h
mandelbrot-book/code/lib/mandelbrot_external_ray_in_native.c
mandelbrot-book/code/lib/mandelbrot_external_ray_in_native.h
mandelbrot-book/code/lib/mandelbrot_binary_angle.c
mandelbrot-book/code/lib/mandelbrot_binary_angle.h
mandelbrot-book/code/lib/pi.c
mandelbrot-book/code/lib/pi.h


--------------------------------------------------------

gcc r.c -std=c99 -Wall -Wextra -pedantic -lm -lgmp -lmpfr
./a.out



*/
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
#include <complex.h>
#include <gmp.h>
#include <mpfr.h>
#include <stdbool.h>



const float pif = 3.14159265358979323846264338327950288419716939937510f;
const double pi = 3.14159265358979323846264338327950288419716939937510;
const long double pil = 3.14159265358979323846264338327950288419716939937510l;



// ------------------------------------------------------------
struct mandelbrot_binary_angle {
  int preperiod;
  int period;
  char *pre;
  char *per;
};

struct mandelbrot_external_ray_in {
  mpq_t angle;
  mpq_t one;
  unsigned int sharpness; // number of steps to take within each dwell band
  unsigned int precision; // delta needs this many bits of effective precision
  unsigned int accuracy;  // epsilon is scaled relative to magnitude of delta
  double escape_radius;
  mpfr_t epsilon2;
  mpfr_t cx;
  mpfr_t cy;
  unsigned int j;
  unsigned int k;
  // temporaries
  mpfr_t zx, zy, dzx, dzy, ux, uy, vx, vy, ccx, ccy, cccx, cccy;
};


// ----------------------------------------------------------------------------



int depth = 0;
mpq_t angle;
int base = 2; // The base can vary from 2 to 62, or if base is 0 then the leading characters are used: 0x or 0X for hex, 0b or 0B for binary, 0 for octal, or decimal otherwise.
char *s;
struct mandelbrot_binary_angle *a ;
mpfr_t cre, cim;

struct mandelbrot_external_ray_in *ray; //  = mandelbrot_external_ray_in_new(angle);


// ----------------------------------------------------------------------------
void mandelbrot_binary_angle_delete(struct mandelbrot_binary_angle *a) {
  free(a->pre);
  free(a->per);
  free(a);
}



// FIXME check canonical form, ie no .01(01) etc
struct mandelbrot_binary_angle *mandelbrot_binary_angle_from_string(const char *s) {
  const char *dot = strchr(s,   '.');
  if (! dot) { return 0; }
  const char *bra = strchr(dot, '(');
  if (! bra) { return 0; }
  const char *ket = strchr(bra, ')');
  if (! ket) { return 0; }
  if (s[0] != '.') { return 0; }
  if (ket[1] != 0) { return 0; }
  struct mandelbrot_binary_angle *a = malloc(sizeof(struct mandelbrot_binary_angle));
  a->preperiod = bra - dot - 1;
  a->period = ket - bra - 1;
  fprintf( stderr	, "external angle \n");
  fprintf( stderr	, "\thas preperiod = %d \t period = %d\n",  a->preperiod,  a->period);
  
  if (a->period < 1) {
    free(a);
    return 0;
  }
  a->pre = malloc(a->preperiod + 1);
  a->per = malloc(a->period + 1);
  memcpy(a->pre, dot + 1, a->preperiod);
  memcpy(a->per, bra + 1, a->period);
  a->pre[a->preperiod] = 0;
  a->per[a->period] = 0;
  for (int i = 0; i < a->preperiod; ++i) {
    if (a->pre[i] != '0' && a->pre[i] != '1') {
      mandelbrot_binary_angle_delete(a);
      return 0;
    }
  }
  for (int i = 0; i < a->period; ++i) {
    if (a->per[i] != '0' && a->per[i] != '1') {
      mandelbrot_binary_angle_delete(a);
      return 0;
    }
  }
  return a;
}


void mandelbrot_binary_angle_to_rational(mpq_t r, const struct mandelbrot_binary_angle *t) {
  mpq_t pre, per;
  mpq_init(pre);
  mpq_init(per);
  mpz_set_str(mpq_numref(pre), t->pre, 2);
  mpz_set_si(mpq_denref(pre), 1);
  mpz_mul_2exp(mpq_denref(pre), mpq_denref(pre), t->preperiod);
  mpq_canonicalize(pre);
  mpz_set_str(mpq_numref(per), t->per, 2);
  mpz_set_si(mpq_denref(per), 1);
  mpz_mul_2exp(mpq_denref(per), mpq_denref(per), t->period);
  mpz_sub_ui(mpq_denref(per), mpq_denref(per), 1);
  mpz_mul_2exp(mpq_denref(per), mpq_denref(per), t->preperiod);
  mpq_canonicalize(per);
  mpq_add(r, pre, per);
  mpq_clear(pre);
  mpq_clear(per);
}

// -------------------------------------------------------------

struct mandelbrot_external_ray_in *mandelbrot_external_ray_in_new(mpq_t angle) {
  struct mandelbrot_external_ray_in *r = malloc(sizeof(struct mandelbrot_external_ray_in));
  mpq_init(r->angle);
  mpq_set(r->angle, angle);
  mpq_init(r->one);
  mpq_set_ui(r->one, 1, 1);
  r->sharpness = 4;
  r->precision = 4;
  r->accuracy  = 4;
  r->escape_radius = 65536.0;
  mpfr_init2(r->epsilon2, 53);
  mpfr_set_ui(r->epsilon2, 1, GMP_RNDN);
  double a = 2.0 * pi * mpq_get_d(r->angle);
  mpfr_init2(r->cx, 53);
  mpfr_init2(r->cy, 53);
  mpfr_set_d(r->cx, r->escape_radius * cos(a), GMP_RNDN);
  mpfr_set_d(r->cy, r->escape_radius * sin(a), GMP_RNDN);
  r->k = 0;
  r->j = 0;
  // initialize temporaries
  mpfr_inits2(53, r->zx, r->zy, r->dzx, r->dzy, r->ux, r->uy, r->vx, r->vy, r->ccx, r->ccy, r->cccx, r->cccy, (mpfr_ptr) 0);
  return r;
}

int mandelbrot_external_ray_in_step(struct mandelbrot_external_ray_in *r) {
  if (r->j >= r->sharpness) {
    mpq_mul_2exp(r->angle, r->angle, 1);
    if (mpq_cmp_ui(r->angle, 1, 1) >= 0) {
      mpq_sub(r->angle, r->angle, r->one);
    }
    r->k++;
    r->j = 0;
  }
  // r0 <- er ** ((1/2) ** ((j + 0.5)/sharpness))
  // t0 <- r0 cis(2 * pi * angle)
  double r0 = pow(r->escape_radius, pow(0.5, (r->j + 0.5) / r->sharpness));
  double a0 = 2.0 * pi * mpq_get_d(r->angle);
  double t0x = r0 * cos(a0);
  double t0y = r0 * sin(a0);
  // c <- r->c
  mpfr_set(r->ccx, r->cx, GMP_RNDN);
  mpfr_set(r->ccy, r->cy, GMP_RNDN);
  for (unsigned int i = 0; i < 64; ++i) { // FIXME arbitrary limit
    // z <- 0
    // dz <- 0
    mpfr_set_ui(r->zx, 0, GMP_RNDN);
    mpfr_set_ui(r->zy, 0, GMP_RNDN);
    mpfr_set_ui(r->dzx, 0, GMP_RNDN);
    mpfr_set_ui(r->dzy, 0, GMP_RNDN);
    // iterate
    for (unsigned int p = 0; p <= r->k; ++p) {
      // dz <- 2 z dz + 1
      mpfr_mul(r->ux, r->zx, r->dzx, GMP_RNDN);
      mpfr_mul(r->uy, r->zy, r->dzy, GMP_RNDN);
      mpfr_mul(r->vx, r->zx, r->dzy, GMP_RNDN);
      mpfr_mul(r->vy, r->zy, r->dzx, GMP_RNDN);
      mpfr_sub(r->dzx, r->ux, r->uy, GMP_RNDN);
      mpfr_add(r->dzy, r->vx, r->vy, GMP_RNDN);
      mpfr_mul_2ui(r->dzx, r->dzx, 1, GMP_RNDN);
      mpfr_mul_2ui(r->dzy, r->dzy, 1, GMP_RNDN);
      mpfr_add_ui(r->dzx, r->dzx, 1, GMP_RNDN);
      // z <- z^2 + c
      mpfr_sqr(r->ux, r->zx, GMP_RNDN);
      mpfr_sqr(r->uy, r->zy, GMP_RNDN);
      mpfr_sub(r->vx, r->ux, r->uy, GMP_RNDN);
      mpfr_mul(r->vy, r->zx, r->zy, GMP_RNDN);
      mpfr_mul_2ui(r->vy, r->vy, 1, GMP_RNDN);
      mpfr_add(r->zx, r->vx, r->ccx, GMP_RNDN);
      mpfr_add(r->zy, r->vy, r->ccy, GMP_RNDN);
    }
    // c' <- c - (z - t0) / dz
    mpfr_sqr(r->ux, r->dzx, GMP_RNDN);
    mpfr_sqr(r->uy, r->dzy, GMP_RNDN);
    mpfr_add(r->vy, r->ux, r->uy, GMP_RNDN);
    mpfr_sub_d(r->zx, r->zx, t0x, GMP_RNDN);
    mpfr_sub_d(r->zy, r->zy, t0y, GMP_RNDN);
    mpfr_mul(r->ux, r->zx, r->dzx, GMP_RNDN);
    mpfr_mul(r->uy, r->zy, r->dzy, GMP_RNDN);
    mpfr_add(r->vx, r->ux, r->uy, GMP_RNDN);
    mpfr_div(r->ux, r->vx, r->vy, GMP_RNDN);
    mpfr_sub(r->cccx, r->ccx, r->ux, GMP_RNDN);
    mpfr_mul(r->ux, r->zy, r->dzx, GMP_RNDN);
    mpfr_mul(r->uy, r->zx, r->dzy, GMP_RNDN);
    mpfr_sub(r->vx, r->ux, r->uy, GMP_RNDN);
    mpfr_div(r->uy, r->vx, r->vy, GMP_RNDN);
    mpfr_sub(r->cccy, r->ccy, r->uy, GMP_RNDN);
    // delta^2 = |c' - c|^2
    mpfr_sub(r->ux, r->cccx, r->ccx, GMP_RNDN);
    mpfr_sub(r->uy, r->cccy, r->ccy, GMP_RNDN);
    mpfr_sqr(r->vx, r->ux, GMP_RNDN);
    mpfr_sqr(r->vy, r->uy, GMP_RNDN);
    mpfr_add(r->ux, r->vx, r->vy, GMP_RNDN);
    // enough_bits = 0 < 2 * prec(eps^2) + exponent eps^2 - 2 * precision
    int enough_bits = 0 < 2 * (mpfr_get_prec(r->epsilon2) - r->precision) + mpfr_get_exp(r->epsilon2);
    if (enough_bits) {
      // converged = delta^2 < eps^2
      int converged = mpfr_less_p(r->ux, r->epsilon2);
      if (converged) {
        // eps^2 <- |c' - r->c|^2 >> (2 * accuracy)
        mpfr_sub(r->ux, r->cccx, r->cx, GMP_RNDN);
        mpfr_sub(r->uy, r->cccy, r->cy, GMP_RNDN);
        mpfr_sqr(r->vx, r->ux, GMP_RNDN);
        mpfr_sqr(r->vy, r->uy, GMP_RNDN);
        mpfr_add(r->ux, r->vx, r->vy, GMP_RNDN);
        mpfr_div_2ui(r->epsilon2, r->ux, 2 * r->accuracy, GMP_RNDN);
        // j <- j + 1
        r->j = r->j + 1;
        // r->c <- c'
        mpfr_set(r->cx, r->cccx, GMP_RNDN);
        mpfr_set(r->cy, r->cccy, GMP_RNDN);
        return 1;
      }
    } else {
      // bump precision
      mpfr_prec_t prec = mpfr_get_prec(r->cx) + 32;
      mpfr_prec_round(r->cx, prec, GMP_RNDN);
      mpfr_prec_round(r->cy, prec, GMP_RNDN);
      mpfr_prec_round(r->epsilon2, prec, GMP_RNDN);
      mpfr_set_prec(r->ccx, prec);
      mpfr_set_prec(r->ccy, prec);
      mpfr_set_prec(r->cccx, prec);
      mpfr_set_prec(r->cccy, prec);
      mpfr_set_prec(r->zx, prec);
      mpfr_set_prec(r->zy, prec);
      mpfr_set_prec(r->dzx, prec);
      mpfr_set_prec(r->dzy, prec);
      mpfr_set_prec(r->ux, prec);
      mpfr_set_prec(r->uy, prec);
      mpfr_set_prec(r->vx, prec);
      mpfr_set_prec(r->vy, prec);
      i = 0;
      // c <- r->c
      mpfr_set(r->cccx, r->cx, GMP_RNDN);
      mpfr_set(r->cccy, r->cy, GMP_RNDN);
    }
    mpfr_set(r->ccx, r->cccx, GMP_RNDN);
    mpfr_set(r->ccy, r->cccy, GMP_RNDN);
  }
  return 0;
}

void mandelbrot_external_ray_in_get(struct mandelbrot_external_ray_in *r, mpfr_t x, mpfr_t y) {
  mpfr_set_prec(x, mpfr_get_prec(r->cx));
  mpfr_set(x, r->cx, GMP_RNDN);
  mpfr_set_prec(y, mpfr_get_prec(r->cy));
  mpfr_set(y, r->cy, GMP_RNDN);
}



void mandelbrot_external_ray_in_delete(struct mandelbrot_external_ray_in *r) {
  mpfr_clear(r->epsilon2);
  mpfr_clear(r->cx);
  mpfr_clear(r->cy);
  mpq_clear(r->angle);
  mpq_clear(r->one);
  mpfr_clears(r->zx, r->zy, r->dzx, r->dzy, r->ux, r->uy, r->vx, r->vy, r->ccx, r->ccy, r->cccx, r->cccy, (mpfr_ptr) 0);
  free(r);
}

// -------------------------------------------------------------------------------------------------------

void PrintCInfo (void)
{

  fprintf(stderr,"gcc version: %d.%d.%d\n", __GNUC__, __GNUC_MINOR__, __GNUC_PATCHLEVEL__);	// https://stackoverflow.com/questions/20389193/how-do-i-check-my-gcc-c-compiler-version-for-my-eclipse
  // OpenMP version is displayed in the console : export  OMP_DISPLAY_ENV="TRUE"

  fprintf(stderr,"__STDC__ = %d\n", __STDC__);
  fprintf(stderr,"__STDC_VERSION__ = %ld\n", __STDC_VERSION__);
  fprintf(stderr,"c dialect = ");
  switch (__STDC_VERSION__)
    {				// the format YYYYMM 
    case 199409L:
      fprintf(stderr,"C94\n");
      break;
    case 199901L:
      fprintf(stderr,"C99\n");
      break;
    case 201112L:
      fprintf(stderr,"C11\n");
      break;
    case 201710L:
      fprintf(stderr,"C18\n");
      break;
      //default : /* Optional */
      }
      //gmp_printf (" GMP-%s \n ", gmp_version );
      mpfr_printf("Versions: MPFR-%s \n GMP-%s \n", mpfr_version, gmp_version );

    

}

void PrintInfo(void){

	//
	fprintf(stderr, "console C program  ( CLI ) for computing external ray of Mandelbrot set (parametric ray)\n"); 
	fprintf(stderr, "using Newton method described by Tomoki Kawahira \n"); 
	fprintf(stderr, "tracing inward ( from infinity toward Mandelbrot set) = ray-in\n"); 
	fprintf(stderr, "arbitrary precision (gmp, mpfr) with dynamic precision adjustment.\n Based on the code by Claude Heiland-Allen: https://mathr.co.uk/web/\n"); 
	fprintf(stderr, "usage: ./a.out angle depth\n outputs space-separated complex numbers on stdout\n example command \n./a.out 1/3 25\n or\n ./a.out .(01) 25\n");
	fprintf( stderr	, "\n");
  	fprintf( stderr	, "\tsharpness = %d\n", ray->sharpness);
  	fprintf( stderr	, "\tprecision = %d\n", ray->precision);
  	fprintf( stderr	, "\taccuracy = %d\n", ray->accuracy);
  	fprintf( stderr	, "\tescape_radius = %.0f\n", ray->escape_radius);
	// 
	PrintCInfo();
}


int setup(void){
	// 2 parameters of external ray : depth, angle
	depth  = 35;
	// external angle 
	s = ".(01)";  // landing point c = -0.750000000000000  +0.000000000000000 i    period = 10000
	// mpq
	mpq_init(angle);
	// mpq init from string or 2 integers
	
	a = mandelbrot_binary_angle_from_string(s); // set a from string 
	// gmp_fprintf (stderr, "\tas a binary fraction = %0b\n", a); // 0b or 0B for binary // not works
    	if (a) {
      		mandelbrot_binary_angle_to_rational(angle, a); // convert binary string to decimal rational number
      		mandelbrot_binary_angle_delete(a); } // use only rational form so delete string form
		
	mpq_canonicalize (angle); // It is the responsibility of the user to canonicalize the assigned variable before any arithmetic operations are performed on that variable.
	
	gmp_fprintf (stderr, "\tas a decimal rational number = %Qd\n", angle); // 
	fprintf( stderr	, "\tas a formated binary string = 0%s\n", s);
	
	
	// ---------------------------------------------------
	
	mpfr_init2(cre, 53);
	mpfr_init2(cim, 53);
	
	
	return 0;
}


int compute_ray(mpq_t angle){



	
	
	ray = mandelbrot_external_ray_in_new(angle);
	if (ray ==NULL ){ fprintf(stderr, " ray error \n"); return 1;}
	
	for (int i = 0; i < depth * 4; ++i) { // FIXME 4 = implementation's sharpness
		//fprintf( stderr	, "i = %d\n", i);
		mandelbrot_external_ray_in_step(ray); //fprintf(stderr, " ray step ok \n");
		mandelbrot_external_ray_in_get(ray, cre, cim); //fprintf(stderr, " ray get ok \n");
		mpfr_out_str(stdout, 10, 0, cre, GMP_RNDN);
		
		putchar(' ');
		mpfr_out_str(stdout, 10, 0, cim, GMP_RNDN);
		putchar('\n');
		}
	
	
	return 0;



}




int end(void){

	PrintInfo();
	fprintf(stderr, " allways free memory (deallocate )  to avoid memory leaks \n");	// wikipedia C_dynamic_memory_allocation
	mpq_clear (angle);
	mpfr_clear(cre);
	mpfr_clear(cim);
	mandelbrot_external_ray_in_delete(ray);
	return 0;
}

int main(void){
	
	setup();

	compute_ray(angle);
	end();

	return 0;
}

Python

过程中的射线

r"""
Mandelbrot and Julia sets (Cython helper)

This is the helper file providing functionality for mandel_julia.py.
https://git.sagemath.org/sage.git/tree/src/sage/dynamics/complex_dynamics/mandel_julia_helper.pyx?id=bf9df0d7ff4f272b19293fd0d04ef3a649d05863

AUTHORS:

- Ben Barros

"""

#*****************************************************************************
#       Copyright (C) 2017 BEN BARROS <[email protected]>
#
# This program is free software: you can redistribute it and/or modify
# it under the terms of the GNU General Public License as published by
# the Free Software Foundation, either version 2 of the License, or
# (at your option) any later version.
#                  http://www.gnu.org/licenses/
#*****************************************************************************

from __future__ import absolute_import, division
from sage.plot.colors import Color
from sage.repl.image import Image
from copy import copy
from cysignals.signals cimport sig_check
from sage.rings.complex_field import ComplexField
from sage.functions.log import exp, log
from sage.symbolic.constants import pi


def external_ray(theta, **kwds):
    r"""
    Draws the external ray(s) of a given angle (or list of angles)
    by connecting a finite number of points that were approximated using
    Newton's method. The algorithm used is described in a paper by
    Tomoki Kawahira.
    https://git.sagemath.org/sage.git/tree/src/sage/dynamics/complex_dynamics/mandel_julia.py?id=bf9df0d7ff4f272b19293fd0d04ef3a649d05863
    REFERENCE:

    [Kaw2009]_

    INPUT:

    - ``theta`` -- double or list of doubles, angles between 0 and 1 inclusive.

    kwds:

    - ``image`` -- 24-bit RGB image (optional - default: None) user specified image of Mandelbrot set.

    - ``D`` -- long (optional - default: ``25``) depth of the approximation. As ``D`` increases, the external ray gets closer to the boundary of the Mandelbrot set. If the ray doesn't reach the boundary of the Mandelbrot set, increase ``D``.

    - ``S`` -- long (optional - default: ``10``) sharpness of the approximation. Adjusts the number of points used to approximate the external ray (number of points is equal to ``S*D``). If ray looks jagged, increase ``S``.

    - ``R`` -- long (optional - default: ``100``) radial parameter. If ``R`` is large, the external ray reaches sufficiently close to infinity. If ``R`` is too small, Newton's method may not converge to the correct ray.

    - ``prec`` -- long (optional - default: ``300``) specifies the bits of precision used by the Complex Field when using Newton's method to compute points on the external ray.

    - ``ray_color`` -- RGB color (optional - default: ``[255, 255, 255]``) color of the external ray(s).

    OUTPUT:

    24-bit RGB image of external ray(s) on the Mandelbrot set.

    EXAMPLES::

        sage: external_ray(1/3)
        500x500px 24-bit RGB image

    ::

        sage: external_ray(0.6, ray_color=[255, 0, 0])
        500x500px 24-bit RGB image

    ::

        sage: external_ray([0, 0.2, 0.4, 0.7]) # long time
        500x500px 24-bit RGB image

    ::

        sage: external_ray([i/5 for i in range(1,5)]) # long time
        500x500px 24-bit RGB image

    WARNING:

    If you are passing in an image, make sure you specify
    which parameters to use when drawing the external ray.
    For example, the following is incorrect::

        sage: M = mandelbrot_plot(x_center=0) # not tested
        sage: external_ray(5/7, image=M) # not tested
        500x500px 24-bit RGB image

    To get the correct external ray, we adjust our parameters::

        sage: M = mandelbrot_plot(x_center=0) # not tested
        sage: external_ray(5/7, x_center=0, image=M) # not tested
        500x500px 24-bit RGB image

    TODO:

    The ``copy()`` function for bitmap images needs to be implemented in Sage.
    """

    x_0 = kwds.get("x_center", -1)
    y_0 = kwds.get("y_center", 0)
    plot_width = kwds.get("image_width", 4)
    pixel_width = kwds.get("pixel_count", 500)
    depth = kwds.get("D", 25)
    sharpness = kwds.get("S", 10)
    radial_parameter = kwds.get("R", 100)
    precision = kwds.get("prec", 300)
    precision = max(precision, -log(pixel_width * 0.001, 2).round() + 10)
    ray_color = kwds.get("ray_color", [255]*3)
    image = kwds.get("image", None)
    if image is None:
        image = mandelbrot_plot(**kwds)

    # Make a copy of the bitmap image.
    # M = copy(image)
    old_pixel = image.pixels()
    M = Image('RGB', (pixel_width, pixel_width))
    pixel = M.pixels()
    for i in range(pixel_width):
        for j in range(pixel_width):
            pixel[i,j] = old_pixel[i,j]

    # Make sure that theta is a list so loop below works
    if type(theta) != list:
        theta = [theta]

    # Check if theta is in the invterval [0,1]
    for angle in theta:
        if angle < 0 or angle > 1:
            raise \
            ValueError("values for theta must be in the closed interval [0,1].")

    # Loop through each value for theta in list and plot the external ray.
    for angle in theta:
        E = fast_external_ray(angle, D=depth, S=sharpness, R=radial_parameter,
         prec=precision, image_width=plot_width, pixel_count=pixel_width)

        # Convert points to pixel coordinates.
        pixel_list = convert_to_pixels(E, x_0, y_0, plot_width, pixel_width)

        # Find the pixels between points in pixel_list.
        extra_points = []
        for i in range(len(pixel_list) - 1):
            if min(pixel_list[i+1]) >= 0 and max(pixel_list[i+1]) < pixel_width:
                for j in get_line(pixel_list[i], pixel_list[i+1]):
                    extra_points.append(j)

        # Add these points to pixel_list to fill in gaps in the ray.
        pixel_list += extra_points

        # Remove duplicates from list.
        pixel_list = list(set(pixel_list))

        # Check if point is in window and if it is, plot it on the image to
        # create an external ray.
        for k in pixel_list:
            if max(k) < pixel_width and min(k) >= 0:
                pixel[int(k[0]), int(k[1])] = tuple(ray_color)
    return M




cpdef fast_external_ray(double theta, long D=30, long S=10, long R=100,
 long pixel_count=500, double image_width=4, long prec=300):
    r"""
    Returns a list of points that approximate the external ray for a given angle.

    INPUT:

    - ``theta`` -- double, angle between 0 and 1 inclusive.

    - ``D`` -- long (optional - default: ``25``) depth of the approximation. As ``D`` increases, the external ray gets closer to the boundary of the Mandelbrot set.

    - ``S`` -- long (optional - default: ``10``) sharpness of the approximation. Adjusts the number of points used to approximate the external ray (number of points is equal to ``S*D``).

    - ``R`` -- long (optional - default: ``100``) radial parameter. If ``R`` is sufficiently large, the external ray reaches enough close to infinity.

    - ``pixel_count`` -- long (optional - default: ``500``) side length of image in number of pixels.

    - ``image_width`` -- double (optional - default: ``4``) width of the image in the complex plane.

    - ``prec`` -- long (optional - default: ``300``) specifies the bits of precision used by the Complex Field when using Newton's method to compute points on the external ray.

    OUTPUT:

    List of tuples of Real Interval Field Elements

    EXAMPLES::

        sage: from sage.dynamics.complex_dynamics.mandel_julia_helper import fast_external_ray
        sage: fast_external_ray(0,S=1,D=1)
        [(100.000000000000000000000000000000000000000000000000000000000000000000000000000000000000000,
          0.000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000),
         (9.51254777713729174697578576623132297117784691109499464854806785133621315075854778426714908,
          0.000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000)]


    ::

        sage: from sage.dynamics.complex_dynamics.mandel_julia_helper import fast_external_ray
        sage: fast_external_ray(1/3,S=1,D=1)
        [(-49.9999999999999786837179271969944238662719726562500000000000000000000000000000000000000000,
          86.6025403784438765342201804742217063903808593750000000000000000000000000000000000000000000),
         (-5.50628047023173006234970878097113901879832542655926629309001652388544528575532346900138516,
          8.64947510053972513843999918917106032664030380426885745306040284140385975750462108180377187)]

    ::

        sage: from sage.dynamics.complex_dynamics.mandel_julia_helper import fast_external_ray
        sage: fast_external_ray(0.75234,S=1,D=1)
        [(1.47021239172637052661229972727596759796142578125000000000000000000000000000000000000000000,
          -99.9891917935294287644865107722580432891845703125000000000000000000000000000000000000000000),
         (-0.352790406744857508500937144524776555433184352559852962308757189778284058275081335121601384,
          -9.98646630765023514178761177926164047797465369576787921409326037870837930920646860774032363)]
    """

    cdef:
        CF = ComplexField(prec)
        PI = CF.pi()
        I = CF.gen()
        c_0, r_m, t_m, temp_c, C_k, D_k, old_c, x, y, dist
        int k, j, t
        double difference, m
        double error = pixel_count * 0.0001

        double pixel_width = image_width / pixel_count

        # initialize list with c_0
        c_list = [CF(R*exp(2*PI*I*theta))]

    # Loop through each subinterval and approximate point on external ray.
    for k in range(1,D+1):
        for j in range(1,S+1):
            m = (k-1)*S + j
            r_m = CF(R**(2**(-m/S)))
            t_m = CF(r_m**(2**k) * exp(2*PI*I*theta * 2**k))
            temp_c = c_list[-1]
            difference = error

            # Repeat Newton's method until points are close together.
            while error <= difference:
                sig_check()
                old_c = temp_c
                # Recursive formula for iterates of q(z) = z^2 + c
                C_k, D_k = CF(old_c), CF(1)
                for t in range(k):
                    C_k, D_k = C_k**2 + old_c, CF(2)*D_k*C_k + CF(1)
                temp_c = old_c - (C_k - t_m) / D_k   # Newton map
                difference = abs(old_c) - abs(temp_c)

            dist = (2*C_k.abs()*(C_k.abs()).log()) / D_k.abs()
            if dist < pixel_width:
                break
            c_list.append(CF(temp_c))
        if dist < pixel_width:
            break

    # Convert Complex Field elements into tuples.
    for k in range(len(c_list)):
        x,y = c_list[k].real(), c_list[k].imag()
        c_list[k] = (x, y)

    return c_list

测试和精度

角度 $\theta$ 以圈为单位	着陆点 $c_{\infty }$	精度
0	1/4
1/2	-2
1/3	-3/4
1/4	-0.228155493653962 +1.115142508039937i
1/5	-0.154724526314600 +1.031047184160779i
1/6	i
1/10	0.384063957 +0.666805123i

见

沃尔夫·荣格测试 : 角度（以圈为单位）的外部参数射线

1/7（周期 3）
321685687669320/2251799813685247（周期 51）
321685687669322/2251799813685247（周期 51）

角度相差约 $10^{-15}$ ，但对应参数射线的着陆点相差约 0.035。^[16]

参考资料

[1] 维基百科 : 外部射线

[2] Adam Majewski 的 gitlab 仓库：参数外部角度

[3] Adam Epstein 和 Giulio Tiozzo 的 Douady 魔法公式的推广

[4] ractalforums.org : Douady 魔法公式的推广

[5] Mary Wilkerson 的临界前周期二次配对的细分规则构造

[6] 维基百科 : 线段

[7] ractalforums.org: 为分形艺术提供创意帮助

[8] Claude Heiland-Allen

[9] ractalforums : 曼德博集中的寻路

[10] Yi-Chiuan Chen、Tomoki Kawahira、Juan-Ming Yuan 的作为微分方程轨道的不变康托集族 II：Julia 集

[11] Tomoki Kawahira 的绘制曼德博集外部射线的算法

[12] I Quilez 的场线

[13] ractalforums.org: 为分形艺术提供创意帮助

[14] Tomoki Kawahira 的绘制曼德博集外部射线的算法

[15] 使用牛顿法绘制外部射线（由 T Kawahira 描述）

[16] 沃尔夫·荣格的绘制参数射线精度的测试

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[15]

[16]

着陆

问答

参数与动态射线之间的关系

尾流

细分规则

主Misiurewicz点规则

符号动力学

想法

如何近似外部射线？

绘制外部射线意味着什么？

如何计算射线上的一个点？

射线何时着陆 ?

算法

追踪射线

在

向外

牛顿法

变量

半径参数 r

常数值

范围

序列

映射

r 映射

深度

深度和锐度

m

多项式映射 q

映射 t

多项式映射 P

牛顿映射 N

如何计算新值 c m , l + 1 {\displaystyle c_{m,l+1}} ？

牛顿迭代

初始点

代码

c 代码

mpfr

Python

测试和精度

参考资料

如何计算新值 $c_{m,l+1}$ ？