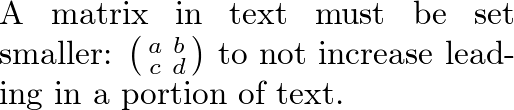LaTeX/数学

LaTeX
入门介绍安装安装额外包基础知识如何获得帮助常用元素文档结构文本格式段落格式颜色字体列表结构特殊字符国际化旋转表格标题创建页面布局自定义页面页眉和页脚‎ 导入图形浮动体、图形和标题脚注和边注超链接标签和交叉引用首字母机制错误和警告长度计数器方框规则和撑杆技术文本数学高级数学定理化学图形算法源代码清单语言学特殊页面索引词汇表参考文献管理更多参考文献特殊文档科学报告（学士报告、硕士论文、博士论文）信件演示文稿教师专区简历学术期刊（MLA、APA 等）创建图形介绍过程图形 MetaPost 图片 PGF/TikZ PSTricks Xy-pic 创建 3D 图形编程宏纯 TeX 创建包创建包文档主题杂项模块化文档协作编写 LaTeX 文档导出到其他格式帮助和建议常见问题解答提示和技巧附录作者链接包参考 LaTeX 文档示例索引命令词汇表
编辑此框 • 编辑目录

°

当唐纳德·克努斯开始开发最初的 TeX 系统时，最伟大的动力之一是创造一种工具，可以简单地构建数学公式，同时在打印时看起来很专业。他成功的事实很可能是 TeX（后来是 LaTeX）在科学界如此受欢迎的原因。排版数学是 LaTeX 最大的优势之一。由于存在大量的数学符号，这也成了一个庞大的话题。

如果你的文档只需要一些简单的数学公式，那么基本的 LaTeX 就包含了你会用到的所有工具。如果你正在编写一篇包含大量复杂公式的科学文档，那么 amsmath 包^[1] 介绍了一些新的命令，这些命令比基本的 LaTeX 提供的命令更强大、更灵活。 mathtools 包修复了 amsmath 的一些问题，并为 amsmath 添加了一些有用的设置、符号和环境。^[2] 为了使用这两个包，在文档的序言中包含

\usepackage{amsmath}

或者

\usepackage{mathtools}

在文档的序言中。 mathtools 包加载了 amsmath 包，因此如果使用 mathtools，则无需在序言中使用 \usepackage{amsmath}。

数学环境

LaTeX 需要知道文本何时是数学文本。这是因为 LaTeX 以不同于普通文本的方式排版数学符号。因此，为这个目的声明了特殊的环境。根据它们如何呈现，可以将它们区分为两类

文本 - 文本公式以行内方式显示，即在声明公式的文本主体中显示，例如，我可以说 $a+a=2a$ 在这句话中。
显示 - 显示的公式在单独的一行上。

由于数学需要特殊的环境，自然地，可以使用标准方式来使用适当的环境名称。但是，与大多数其他环境不同，有一些方便的缩写形式用于声明你的公式。下表总结了它们

类型	行内（文本内）公式	显示的方程式	显示的并自动编号的方程式
环境	`math`	`displaymath`	`equation`
LaTeX 缩写	`$...$`	`\[...\]`
TeX 缩写	$...$	`$$...$$`
注释			`equation*`（带星号的版本）禁止编号，但需要 amsmath

建议：应避免使用 $$...$$，因为它可能会导致问题，尤其是在使用 AMS-LaTeX 宏时。此外，如果出现问题，错误消息可能没有帮助。

equation* 和 displaymath 环境在功能上是等效的。

如果你正在正常输入文本，则称你处于文本模式，但当你输入这些数学环境之一时，则称你处于数学模式，它与文本模式相比有一些不同之处

大多数空格和换行符都没有意义，因为所有空格都是从数学表达式中逻辑地推导出来的，或者必须使用特殊的命令来指定，例如 \quad
不允许空行。每个公式只允许一个段落。
每个字母都被认为是变量的名称，并将按此方式排版。如果你想在公式中排版普通文本（普通直立字体，正常间距），则必须使用专用命令来输入文本。

在文本块中插入“显示”数学

为了让一些操作符，例如 \lim 或 \sum，在一些数学环境（阅读 $......$ ）中正确显示，在环境内部写入 \displaystyle 类可能很方便。这样做可能会导致行变高，但会使一些数学运算符的指数和索引正确显示。例如， $\sum$ 会打印一个较小的 Σ，而 $\displaystyle \sum$ 会打印一个较大的 Σ $\displaystyle \sum$ ，就像在方程式中一样。^{[注 1]} 可以通过在前言中（即在 \begin{document} 之前）声明 \everymath{\displaystyle}，强制所有数学环境都执行此行为。

符号

数学有很多符号！以下是可以直接从键盘访问的一组符号

+ - = ! / ( ) [ ] < > | ' : *

除了上面列出的符号之外，为了显示所需的符号，必须发出不同的命令。有很多例子，例如希腊字母、集合和关系符号、箭头、二元运算符等。

例如

\forall x \in X, \quad \exists y \leq \epsilon

$\forall x\in X,\quad \exists y\leq \epsilon \,$

幸运的是，有一个工具可以大大简化搜索特定符号的命令。在下面的外部链接部分中查找“Detexify”。另一个选择是查看下面的外部链接部分中的“LaTeX 符号列表”。

希腊字母

希腊字母在数学中很常见，而且在数学模式中很容易输入。你只需要在反斜杠后输入字母的名称：如果第一个字母是小写，你将得到一个小写希腊字母；如果第一个字母是大写（并且只有第一个字母是大写），那么你将得到一个大写字母。注意，一些大写希腊字母看起来像拉丁字母，所以 LaTeX 没有提供它们（例如，大写Alpha 和Beta 只是“A”和“B”，分别）。小写 epsilon、theta、kappa、phi、pi、rho 和 sigma 提供了两种不同的版本。备用或变体版本是通过在字母名称之前添加“var”来创建的。

\alpha, \Alpha, \beta, \Beta, \gamma, \Gamma, \pi, \Pi, \phi, \varphi, \mu, \Phi

$\alpha ,\mathrm {A} ,\beta ,\mathrm {B} ,\gamma ,\Gamma ,\pi ,\Pi ,\phi ,\varphi ,\mu ,\Phi$

向下滚动到 #数学符号列表以获取完整的希腊符号列表。

运算符

运算符是一个以单词形式表示的函数：例如三角函数 (sin、cos、tan)、对数和指数函数 (log、exp)、极限 (lim)，以及迹和行列式 (tr、det)。LaTeX 定义了很多这样的函数作为命令

\cos (2\theta) = \cos^2 \theta - \sin^2 \theta

$\cos(2\theta )=\cos ^{2}\theta -\sin ^{2}\theta \,$

对于某些运算符，例如极限，下标放在运算符下方

\lim\limits_{x \to \infty} \exp(-x) = 0

$\lim _{x\to \infty }\exp(-x)=0$

对于模运算符，有两个命令：\bmod 和 \pmod

a \bmod b

$a\,{\bmod {\,}}b\,$

x \equiv a \pmod{b}

$x\equiv a{\pmod {b}}\,$

要使用未预定义的运算符，例如 argmax，请参阅自定义运算符

幂和指数

幂和指数等效于普通文本模式中的上标和下标。插入符号 (^; 也称为抑音符) 字符用于提升某物，而下划线 (_) 用于降低某物。如果包含多个字符的表达式被提升或降低，则应使用花括号 ({ 和 }) 进行分组。

k_{n+1} = n^2 + k_n^2 - k_{n-1}

$k_{n+1}=n^{2}+k_{n}^{2}-k_{n-1}\,$

对于多位数的幂，用 {} 将幂括起来。

x^{1.01}

$x^{1.01}\,$

下划线 (_) 可以与竖线 ( $|$ ) 一起使用，以在数学中表示使用下标表示法的求值。

f(n) = n^5 + 4n^2 + 2 |_{n=17}

$f(n)=n^{5}+4n^{2}+2|_{n=17}\,$

分数和二项式

分数使用 \frac{numerator}{denominator} 命令创建（对于那些需要刷新记忆的人来说，那就是分别是 *顶部* 和 *底部*！）。类似地，二项式系数（也称为选择函数）可以使用 \binom 命令编写：^{[注 1]}

\frac{n!}{k!(n-k)!} = \binom{n}{k}

${\frac {n!}{k!(n-k)!}}={\binom {n}{k}}$

您可以在分数中嵌套分数

\frac{\frac{1}{x}+\frac{1}{y}}{y-z}

${\frac {{\frac {1}{x}}+{\frac {1}{y}}}{y-z}}$

请注意，当出现在另一个分数内部或内联文本中时 ${\tfrac {a}{b}}$ ，分数明显小于显示的数学。 \tfrac 和 \dfrac 命令^{[注 1]} 强制使用各自的样式，\textstyle 和 \displaystyle。类似地，\tbinom 和 \dbinom 命令排版二项式系数。

对于相对简单的分数，特别是在文本中，使用幂和索引可能会在美学上更令人愉悦。

^3/_7

$^{1}/_{x}\,$

如果这看起来有点“松散”（即间距过大），可以通过插入一些负间距来定义一个更紧凑的版本。

%running fraction with slash - requires math mode.
\newcommand*\rfrac[2]{{}^{#1}\!/_{#2}}

\rfrac{3}{7}

${{}^{3}\!/_{7}}$

如果您在整个文档中使用它们，建议使用 xfrac 包。此包提供 \sfrac 命令来创建倾斜分数。用法

Take $\sfrac{1}{2}$ cup of sugar, \dots
 
  3\times\sfrac{1}{2}=1\sfrac{1}{2}
 

Take ${}^1/_2$ cup of sugar, \dots
 
  3\times{}^1/_2=1{}^1/_2

如果分数用作指数，则必须在 \sfrac 命令周围使用花括号。

 $x^\frac{1}{2}$ % no error
 $x^\sfrac{1}{2}$ % error
 $x^{\sfrac{1}{2}}$ % no error

$x^\frac{1}{2}$ % no error

$t^{\frac {5}{2}}$

在某些情况下，仅使用该包会导致有关某些字体形状不可用的错误。在这种情况下，还需要添加 lmodern 和 fix-cm 包。

或者，nicefrac 包提供了 \nicefrac 命令，其用法类似于 \sfrac。

连分数

连分数应该使用 \cfrac 命令编写：^{[注 1]}

\begin{equation}
  x = a_0 + \cfrac{1}{a_1 
          + \cfrac{1}{a_2 
          + \cfrac{1}{a_3 + \cfrac{1}{a_4} } } }
\end{equation}

$x=a_{0}+{\cfrac {1}{a_{1}+{\cfrac {1}{a_{2}+{\cfrac {1}{a_{3}+{\cfrac {1}{a_{4}}}}}}}}}$

两个数的乘法

为了使乘法在视觉上类似于分数，可以使用嵌套数组。例如，将上下排列的数字相乘可以按如下方式排版

\begin{equation}
\frac{
    \begin{array}[b]{r}
      \left( x_1 x_2 \right)\\
      \times \left( x'_1 x'_2 \right)
    \end{array}
  }{
    \left( y_1y_2y_3y_4 \right)
  }
\end{equation}

${\frac {\begin{array}{r}\left(x_{1}x_{2}\right)\\\times \left(x'_{1}x'_{2}\right)\end{array}}{\left(y_{1}y_{2}y_{3}y_{4}\right)}}$

根式

\sqrt 命令创建一个围绕表达式的平方根。它接受一个可选参数，该参数在方括号（[ 和 ]）中指定以更改幅度

\sqrt{\frac{a}{b}}

${\sqrt {\frac {a}{b}}}$

\sqrt[n]{1+x+x^2+x^3+\dots+x^n}

${\sqrt[{n}]{1+x+x^{2}+x^{3}+\dots +x^{n}}}$

有些人更喜欢在根号的“封闭”处写根号，覆盖其内容。这种方法可能使根号范围内的内容更清晰。这种习惯通常不在计算机写作中使用，但是如果您仍然想改变平方根的输出，LaTeX 为您提供了这种可能性。只需在文档的序言中添加以下代码

% New definition of square root:
% it renames \sqrt as \oldsqrt
\let\oldsqrt\sqrt
% it defines the new \sqrt in terms of the old one
\def\sqrt{\mathpalette\DHLhksqrt}
\def\DHLhksqrt#1#2{%
\setbox0=\hbox{$#1\oldsqrt{#2\,}$}\dimen0=\ht0
\advance\dimen0-0.2\ht0
\setbox2=\hbox{\vrule height\ht0 depth -\dimen0}%
{\box0\lower0.4pt\box2}}

此 TeX 代码首先将 \sqrt 命令重命名为 \oldsqrt，然后根据旧的命令重新定义 \sqrt，添加更多内容。左侧图片中的新平方根与右侧的旧平方根进行了比较。不幸的是，如果您想使用多个根号，此代码将不起作用：如果您尝试在使用上述代码后编写 ${\sqrt[{b}]{a}}$ 作为 \sqrt[b]{a}，您只会得到错误的输出。换句话说，只有在整个文档中不使用多个根号的情况下，才能以这种方式重新定义平方根。

允许使用多个根号的另一种 TeX 代码是

\usepackage{letltxmacro}
\makeatletter
\let\oldr@@t\r@@t
\def\r@@t#1#2{%
\setbox0=\hbox{$\oldr@@t#1{#2\,}$}\dimen0=\ht0
\advance\dimen0-0.2\ht0
\setbox2=\hbox{\vrule height\ht0 depth -\dimen0}%
{\box0\lower0.4pt\box2}}
\LetLtxMacro{\oldsqrt}{\sqrt}
\renewcommand*{\sqrt}[2][\ ]{\oldsqrt[#1]{#2} }
\makeatother


$\sqrt[a]{b} \quad \oldsqrt[a]{b}$

但是，这需要 \usepackage{letltxmacro} 包。

求和与积分

\sum 和 \int 命令分别插入求和符号和积分符号，使用插入符号 (^) 和下划线 (_) 指定限制。求和的典型符号是

\sum_{i=1}^{10} t_i

$\textstyle \sum _{i=1}^{10}t_{i}\,$

或者

\displaystyle\sum_{i=1}^{10} t_i

$\displaystyle \sum _{i=1}^{10}t_{i}\,$

积分的限制遵循相同的符号。同样重要的是要用一个直立的 d 表示积分变量，在数学模式下，它是通过 \mathrm{} 命令获得的，并且用一个小的空格将它与被积函数分开，这是通过 \, 命令实现的。

\int_0^\infty \mathrm{e}^{-x}\,\mathrm{d}x

$\int _{0}^{\infty }\mathrm {e} ^{-x}\,\mathrm {d} x\,$

还有许多其他以类似方式运作的“大型”命令。

`\sum`	$\sum \,$	`\prod`	$\prod$	`\coprod`	$\coprod$
`\bigoplus`	$\bigoplus$	`\bigotimes`	$\bigotimes$	`\bigodot`	$\bigodot$
`\bigcup`	$\bigcup$	`\bigcap`	$\bigcap$	`\biguplus`	$\biguplus$
`\bigsqcup`	$\bigsqcup$	`\bigvee`	$\bigvee$	`\bigwedge`	$\bigwedge$
`\int`	$\int$	`\oint`	$\oint$	`\iint`^{[note 1]}	$\iint$
`\iiint`^{[note 1]}	$\iiint$	`\iiiint`^{[note 1]}	$\iiiint$	`\idotsint`^{[note 1]}	$\int \!\cdots \!\int$

有关更多积分符号，包括默认情况下未包含在 Computer Modern 字体中的符号，请尝试使用 esint 包。

\substack 命令^{[note 1]} 允许使用 \\ 在多行上写入极限。

\sum_{\substack{
   0<i<m \\
   0<j<n
  }} 
 P(i,j)

$\sum _{\overset {\scriptstyle 0<i<m}{\scriptstyle 0<j<n}}P(i,j)\,$

如果你想要积分的上下限出现在符号的上方和下方（像求和符号一样），请使用 \limits 命令

\int\limits_a^b

$\int \limits _{b}^{c}\,$

但是，如果你希望这适用于所有积分，最好在加载 amsmath 包时指定 intlimits 选项

\usepackage[intlimits]{amsmath}

下标和上标在其他情况下，以及与它们相关的 amsmath 包的其他参数，在高级数学章节中描述。

对于更大的积分，你可以使用个人声明，或者 bigints 包^[3]。

括号、大括号和分隔符

如何在多行方程中使用大括号在高级数学章节中描述。

当处理除最简单的方程之外的任何内容时，使用分隔符（如括号）变得很重要。如果没有它们，公式可能会变得模棱两可。此外，诸如矩阵之类的特殊类型的数学结构通常依靠分隔符来包围它们。

LaTeX 提供了各种可用于分隔符

( a ), [ b ], \{ c \}, | d |, \| e \|,
\langle f \rangle, \lfloor g \rfloor,
\lceil h \rceil, \ulcorner i \urcorner,
/ j \backslash

$(a),[b],\{c\},|d|,\|e\|,\langle f\rangle ,\lfloor g\rfloor ,\lceil h\rceil ,\ulcorner i\urcorner ,/j\backslash$

其中 \lbrack 和 \rbrack 可用于代替 [ 和 ]。

自动调整大小

通常，数学符号的大小会不同，在这种情况下，包围表达式的分隔符应该相应地变化。可以使用 \left、\right 和 \middle 命令来自动执行此操作。任何前面的分隔符都可以与这些命令结合使用

\left(\frac{x^2}{y^3}\right)

$\left({\frac {x^{2}}{y^{3}}}\right)\,$

P\left(A=2\middle|\frac{A^2}{B}>4\right)

大括号使用 \left\{ 和 \right\} 进行不同的定义，

\left\{\frac{x^2}{y^3}\right\}

$\left\{{\frac {x^{2}}{y^{3}}}\right\}\,$

如果表达式只有一侧需要分隔符，那么可以使用句点 (.) 表示另一侧的不可见分隔符。

\left.\frac{x^3}{3}\right|_0^1

$\left.{\frac {x^{3}}{3}}\right|_{0}^{1}\,$

手动调整大小

在某些情况下，\left 和 \right 命令生成的尺寸可能不理想，或者你可能只想更细致地控制分隔符尺寸。在这种情况下，可以使用 \big、\Big、\bigg 和 \Bigg 修饰符命令

( \big( \Big( \bigg( \Bigg(

$({\big (}{\Big (}{\bigg (}{\Bigg (}\,$

这些命令主要在处理嵌套分隔符时有用。例如，当排版

\frac{\mathrm d}{\mathrm d x} \left( k g(x) \right)

${\frac {\mathrm {d} }{\mathrm {d} x}}\left(kg(x)\right)$

我们注意到 \left 和 \right 命令生成的分隔符大小与嵌套在其中的分隔符大小相同。这可能难以阅读。要解决此问题，我们写道

\frac{\mathrm d}{\mathrm d x} \big( k g(x) \big)

${\frac {\mathrm {d} }{\mathrm {d} x}}{\big (}kg(x){\big )}$

当一个方程式太大，超出页面边缘，必须使用对齐命令将其分成两行时，手动调整大小也很有用。虽然命令\left. 和 \right. 可用于平衡每行上的定界符，但这可能会导致定界符大小错误。此外，手动调整大小可用于避免过大的定界符 - 如果一个 \underbrace 或类似命令出现在定界符之间。

矩阵和数组

可以使用 matrix 环境^{[注 1]} 创建一个基本矩阵：与其他表格结构一样，条目按行指定，列之间用一个 ampersand (&) 分隔，新行之间用双反斜杠 (\\) 分隔。

\[
 \begin{matrix}
  a & b & c \\
  d & e & f \\
  g & h & i
 \end{matrix}
\]

${\begin{matrix}a&b&c\\d&e&f\\g&h&i\end{matrix}}$

要指定表格中列的对齐方式，请使用带星号的版本^{[注 2]}。

\begin{matrix}
  -1 & 3 \\
  2 & -4
 \end{matrix}
 =
 \begin{matrix*}[r]
  -1 & 3 \\
  2 & -4
 \end{matrix*}

${\begin{matrix}-1&3\\2&-4\end{matrix}}={\begin{matrix}-1&\,\;\;3\\\,\;\;2&-4\end{matrix}}$

默认对齐方式是 c，但它可以是 array 环境中有效的任何列类型。

但是，矩阵通常用某种定界符括起来，虽然可以使用 \left 和 \right 命令，但还有各种其他预定义的环境，它们会自动包含定界符。

环境名称	周围定界符	说明
pmatrix^{[注 1]}	$(\,)$	默认情况下将列居中。
pmatrix*^{[注 2]}	$(\,)$	允许在可选参数中指定列的对齐方式。
bmatrix^{[注 1]}	$[\,]$	默认情况下将列居中。
bmatrix*^{[注 2]}	$[\,]$	允许在可选参数中指定列的对齐方式。
Bmatrix^{[注 1]}	$\{\,\}$	默认情况下将列居中。
Bmatrix*^{[注 2]}	$\{\,\}$	允许在可选参数中指定列的对齐方式。
vmatrix^{[注 1]}	$\|\,\|$	默认情况下将列居中。
vmatrix*^{[注 2]}	$\|\,\|$	允许在可选参数中指定列的对齐方式。
Vmatrix^{[注 1]}	$\\|\,\\|$	默认情况下将列居中。
Vmatrix*^{[注 2]}	$\\|\,\\|$	允许在可选参数中指定列的对齐方式。

当写下任意大小的矩阵时，通常使用水平、垂直和对角线三个点（称为省略号）来填充某些列和行。可以使用 \cdots、\vdots 和 \ddots 分别指定它们。

A_{m,n} = 
 \begin{pmatrix}
  a_{1,1} & a_{1,2} & \cdots & a_{1,n} \\
  a_{2,1} & a_{2,2} & \cdots & a_{2,n} \\
  \vdots  & \vdots  & \ddots & \vdots  \\
  a_{m,1} & a_{m,2} & \cdots & a_{m,n} 
 \end{pmatrix}

$A_{m,n}={\begin{pmatrix}a_{1,1}&a_{1,2}&\cdots &a_{1,n}\\a_{2,1}&a_{2,2}&\cdots &a_{2,n}\\\vdots &\vdots &\ddots &\vdots \\a_{m,1}&a_{m,2}&\cdots &a_{m,n}\end{pmatrix}}$

在某些情况下，您可能希望更精细地控制每列中的对齐方式，或者在列或行之间插入线条。这可以使用 array 环境来实现，它本质上是 tabular 环境的数学模式版本，它要求预先指定列。

\begin{array}{c|c}
  1 & 2 \\ 
  \hline
  3 & 4
 \end{array}

${\begin{array}{c|c}1&2\\\hline 3&4\end{array}}$

您可能会发现，当与分数一起使用时，AMS 矩阵类环境不会留下足够的空格，从而导致类似于此的输出。

$M={\begin{bmatrix}{\frac {5}{6}}&{\frac {1}{6}}&0\\{\frac {5}{6}}&0&{\frac {1}{6}}\\0&{\frac {5}{6}}&{\frac {1}{6}}\end{bmatrix}}$

为了解决这个问题，可以通过可选参数在 \\ 命令中添加额外的前导空格。

M = \begin{bmatrix}
       \frac{5}{6} & \frac{1}{6} & 0           \\[0.3em]
       \frac{5}{6} & 0           & \frac{1}{6} \\[0.3em]
       0           & \frac{5}{6} & \frac{1}{6}
     \end{bmatrix}

$M={\begin{bmatrix}{\frac {5}{6}}&{\frac {1}{6}}&0\\[0.3em]{\frac {5}{6}}&0&{\frac {1}{6}}\\[0.3em]0&{\frac {5}{6}}&{\frac {1}{6}}\end{bmatrix}}$

如果您需要在矩阵上添加“边框”或“索引”，则纯TeX提供宏 \bordermatrix。

M = \bordermatrix{~ & x & y \cr
                  A & 1 & 0 \cr
                  B & 0 & 1 \cr}

行文中的矩阵

要插入一个小矩阵，而不增加包含它的行的前导空格，请使用 smallmatrix 环境。

A matrix in text must be set smaller:
$\bigl(\begin{smallmatrix}
a&b \\ c&d
\end{smallmatrix} \bigr)$
to not increase leading in a portion of text.

在方程中添加文本

数学环境在文本表示方面与文本环境不同。以下是一个尝试在数学环境中表示文本的示例。

50 apples \times 100 apples = lots of apples^2

$50apples\times 100apples=lotsofapples^{2}\,$

有两个明显的问题：单词或数字之间没有空格，并且字母是斜体的，并且比正常的文本间距更大。这两个问题仅仅是数学模式的产物，因为它将文本视为数学表达式：空格被忽略（LaTeX根据自己的规则对数学进行空格处理），并且每个字符都是一个独立的元素（因此与普通文本相比，它们的位置不那么紧密）。

有许多方法可以正确添加文本。典型的方法是用 \text{...} 命令^{[note 1]}（类似的命令是 \mbox{...}，尽管这会导致下标出现问题，并且名称没有那么具有描述性）。让我们看看当上述方程代码被修改后会发生什么。

50 \text{apples} \times 100 \text{apples} 
 = \text{lots of apples}^2

$50{\text{apples}}\times 100{\text{apples}}={\text{lots of apples}}^{2}\,$

文本看起来更好了。但是，数字和单词之间没有空格。不幸的是，您需要显式地添加它们。有很多方法可以添加数学元素之间的空格，但为了简单起见，我们可以简单地将空格字符插入 \text 命令中。

50 \text{ apples} \times 100 \text{ apples}
 = \text{lots of apples}^2

$50{\text{ apples}}\times 100{\text{ apples}}={\text{lots of apples}}^{2}\,$

格式化文本

使用 \text 很好，并且可以得到基本结果。但是，还有另一种选择，它提供了更大的灵活性。您可能还记得字体格式化命令的介绍，例如 \textrm，\textit，\textbf 等。这些命令将相应地格式化参数，例如，\textbf{bold text} 会得到 bold text。这些命令在数学环境中同样有效，可以包含文本。这里额外的好处是，您可以更好地控制字体格式，而不是使用 \text 所实现的标准文本。

50 \textrm{ apples} \times 100
 \textbf{ apples} = \textit{lots of apples}^2

$50\;{\textrm {apples}}\times 100\;{\textbf {apples}}={\textit {lotsofapples}}^{2}\,$

格式化数学符号

另见：w:数学字母数字符号、w:帮助：显示公式#字母和字体和 w:维基百科：LaTeX 符号#字体

现在我们可以格式化文本；那么如何格式化数学表达式呢？有一组格式化命令非常类似于刚刚使用的字体格式化命令，只是它们专门针对数学模式下的文本（需要 amsfonts 包）。

LaTeX 命令	示例	描述	常用
`\mathnormal{…}` （或者简单地省略任何命令）	$ABCDEF~abcdef~123456\,$	默认的数学字体	大多数数学符号
`\mathrm{…}`	$\mathrm {ABCDEF~abcdef~123456} \,$	这是默认或正常字体，不斜体	计量单位，单字函数
`\mathit{…}`	${\mathit {ABCDEF~abcdef~123456}}\,$	斜体字体	多字母函数或变量名。与 `\mathnormal` 相比，单词间距更自然，数字也斜体。
`\mathbf{…}`	$\mathbf {ABCDEF~abcdef~123456} \,$	粗体字体	向量
`\mathsf{…}`	${\mathsf {ABCDEF~abcdef~123456}}\,$	无衬线字体	类别
`\mathtt{…}`	${\mathtt {ABCDEF~abcdef~123456}}\,$	等宽（固定宽度）字体
`\mathfrak{…}` （需要 amsfonts 或 amssymb 包^{[注 3]}）	${\mathfrak {ABCDEF~abcdef~123456}}\,$	哥特体	李代数的几乎规范字体，环论中的理想
`\mathcal{…}`	${\mathcal {ABCDEF}}\,$	书法（仅限大写^{[注 3]}）	常用于层/概形和范畴，用于表示密码学概念，例如定义字母表（ ${\mathcal {A}}$ ），消息空间（ ${\mathcal {M}}$ ），密文空间（ ${\mathcal {C}}$ ）和密钥空间（ ${\mathcal {K}}$ ）；克莱尼的 ${\mathcal {O}}$ ；描述逻辑中的命名约定；拉普拉斯变换（ ${\mathcal {L}}$ ）和傅里叶变换（ ${\mathcal {F}}$ )
`\mathbb{…}` （需要amsfonts或amssymb包^{[注 3]}）	$\mathbb {ABCDEF} \,$	黑板粗体（仅大写^{[注 3]}）	用于表示特殊集合（例如，实数）
`\mathscr{…}` （需要mathrsfs包^{[注 3]}）		手写体（仅大写^{[注 3]}）	范畴和层的一种替代字体。

这些格式化命令可以包装在整个方程周围，而不仅仅是文本元素：它们只格式化字母、数字和大写希腊字母，其他数学命令不受影响。

要使小写希腊字母或其他符号变为粗体，请使用\boldsymbol命令^{[注 1]}；这只有在当前字体中存在该符号的粗体版本时才有效。作为最后的手段，可以使用\pmb命令^{[注 1]}（穷人粗体）：它打印多个版本稍微偏移的字符。

\boldsymbol{\beta} = (\beta_1,\beta_2,\dotsc,\beta_n)

${\boldsymbol {\beta }}=(\beta _{1},\beta _{2},\dotsc ,\beta _{n})\,$

要更改数学模式中的字体大小，请参阅更改字体大小。

重音

那么，当你用完符号和字体时该怎么办？好吧，下一步是使用重音

`a'` 或 `a^{\prime}`	$a'\,$	`a''`	$a''\,$
`\hat{a}`	${\hat {a}}\,$	`\bar{a}`	${\bar {a}}\,$
`\grave{a}`	${\grave {a}}\,$	`\acute{a}`	${\acute {a}}\,$
`\dot{a}`	${\dot {a}}\,$	`\ddot{a}`	${\ddot {a}}\,$
`\not{a}`	$\not {a}\,$	`\mathring{a}`	å
`\overrightarrow{AB}`	${\overrightarrow {AB}}\,$	`\overleftarrow{AB}`	${\overleftarrow {AB}}\,$
`a'''`	$a'''\,$	`a''''`	$a''''\,$
`\overline{aaa}`	${\overline {aaa}}\,$	`\check{a}`	${\check {a}}\,$
`\breve{a}`	${\breve {a}}\,$	`\vec{a}`	${\vec {a}}\,$
`\dddot{a}`^{[note 1]}		`\ddddot{a}`^{[note 1]}
`\widehat{AAA}`	${\widehat {AAA}}\,$	`\widetilde{AAA}`	${\widetilde {AAA}}$
`\stackrel\frown{AAA}`	${\stackrel {\frown }{AAA}}$
`\tilde{a}`	${\tilde {a}}\,$	`\underline{a}`	${\underline {a}}\,$

颜色

包 xcolor，在颜色中描述，允许我们为方程添加颜色。例如，

k = {\color{red}x} \mathbin{\color{blue}-} 2

$k={\color {red}x}{\mathbin {\color {blue}-}}2$

唯一的问题是，这破坏了默认的 $L a T e X$ 围绕 - 运算符的格式。要解决此问题，我们将它包含在 \mathbin 环境中，因为 - 是二元运算符。此过程在这里进行了描述。

加号和减号

LaTeX 以两种可能的方式处理 + 和 − 符号。最常见的是作为二元运算符。当符号两侧出现两个数学元素时，它被认为是二元运算符，因此，它在符号两侧分配一些空间。另一种方式是符号指定。这是指明数学量是正还是负。对于后者来说，这很常见，因为在数学中，这样的元素被认为是正的，除非它们前面加了 − 。在这种情况下，您希望符号紧挨着相应的元素，以显示它们的关联性。如果您在 + 或 − 之前没有任何东西，但您希望它像二元运算符一样被处理，则可以在运算符之前使用 {} 添加一个不可见字符。这在您编写多行公式并且新行可能以 − 或 + 开头时很有用，例如，然后您可以添加必要的不可见字符来修复一些奇怪的对齐方式。

加减号写成

\pm

$\pm$

类似地，也存在减加号

\mp

$\mp$

控制水平间距

LaTeX 显然非常擅长排版数学公式——这是 LaTeX 所扩展的核心 TeX 系统的主要目标之一。但是，它并不总是能可靠地按您的意愿解释公式。在存在模棱两可的表达式时，它必须做出某些假设。结果往往是水平间距略有不正确。在这种情况下，输出仍然令人满意，但任何完美主义者无疑都希望微调他们的公式以确保间距正确。这些通常是非常细微的调整。

还有其他一些情况，LaTeX 做得很好，但您只是想添加一些空格，也许是为了添加一些注释。例如，在以下等式中，最好确保数学公式和文本之间有足够的空格。

\[ f(n) =
  \begin{cases}
    n/2       & \quad \text{if } n \text{ is even}\\
    -(n+1)/2  & \quad \text{if } n \text{ is odd}
  \end{cases}
\]

$f(n)={\begin{cases}n/2&\quad {\text{if }}n{\text{ is even}}\\-(n+1)/2&\quad {\text{if }}n{\text{ is odd}}\end{cases}}$

此代码在 Miktex 2.9 中产生错误，并且不会产生右侧显示的结果。使用 \mathrm 而不是 \text。

(请注意，这个特定的示例可以通过 cases 结构以更优雅的代码表达，该结构由 amsmath 包提供，如高级数学章节中所述。）

LaTeX 定义了两个命令，可以在文档的任何位置使用（不仅仅是在数学公式中）来插入一些水平空格。它们是 \quad 和 \qquad

A \quad 是等于当前字体大小的空格。因此，如果您使用的是 11pt 字体，那么 \quad 提供的空格也将是 11pt（当然是水平的）。\qquad 提供两倍的量。从上面示例的代码中可以看出，\quad 用于在数学公式和文本之间添加一些间隔。

好的，现在回到文档开头提到的微调。一个很好的例子是显示 y 关于 x 的不定积分的简单方程

$\int y\,\mathrm {d} x$

如果您要尝试一下，您可以写

\int y \mathrm{d}x

$\int y\mathrm {d} x$

但是，这并没有给出正确的结果。LaTeX 不尊重代码中留下的空格来表示 y 和 dx 是独立的实体。相反，它把它们全部 lumped together。在这种情况下一 \quad 显然是过分了——需要使用一些小空格来在这种情况下使用，而这就是 LaTeX 提供的

命令	描述	大小
`\,`	小空格	3/18 个 quad
`\:`	中等空格	4/18 个 quad
`\;`	大空格	5/18 个 quad
`\!`	负空格	-3/18 个 quad

注意，您可以按顺序使用多个命令来实现更大的空间，如果需要的话。

因此，要纠正当前问题

\int y\, \mathrm{d}x

$\int y\,\mathrm {d} x$

\int y\: \mathrm{d}x

$\int y\;\;\!\!\mathrm {d} x$

\int y\; \mathrm{d}x

$\int y\;\mathrm {d} x$

负空格可能看起来很奇怪，但是，如果它没有某种用途，它就不会存在！以下面的例子为例

\left(
    \begin{array}{c}
      n \\
      r
    \end{array}
  \right) = \frac{n!}{r!(n-r)!}

$\left({\begin{matrix}n\\r\end{matrix}}\right)={\frac {n!}{r!(n-r)!}}$

用于表示二项式系数的矩阵式表达式过于冗长。括号和实际内容之间留有太多空白。这可以通过在左括号后和右括号前添加一些负空格来轻松修正。

\left(\!
    \begin{array}{c}
      n \\
      r
    \end{array}
  \!\right) = \frac{n!}{r!(n-r)!}

$\left(\!{\begin{matrix}n\\r\end{matrix}}\!\right)={\frac {n!}{r!(n-r)!}}$

无论如何，应尽可能避免手动添加空格：这会使源代码更复杂，并且违反了所见即所得方法的基本原则。最好的做法是使用您想要的空格定义一些命令，然后，当您使用命令时，您就不需要添加任何其他空格。之后，如果您改变了对水平空格长度的想法，您可以轻松地更改它，只需要修改之前定义的命令即可。让我们举个例子：您希望积分中dx的d为罗马字体，并且与其余部分有一小段距离。如果您想输入类似于\int x \, \mathrm{d} x的积分，您可以定义一个像这样的命令

\newcommand{\dd}{\mathop{}\,\mathrm{d}}

在文档的前言中。我们选择\dd只是因为它让人想起它所替换的“d”，并且输入速度很快。这样，您积分的代码就变成了\int x \dd x。现在，无论何时您写积分，您只需要使用\dd代替“d”，您所有的积分将具有相同的样式。如果您改变主意，您只需要改变前言中的定义，所有积分将相应地更改。

手动指定公式样式

要手动使用文本样式显示公式的一部分，请用花括号括起该片段，并在该片段前加上\textstyle。需要花括号，因为\textstyle宏会改变渲染器状态，以文本样式渲染所有后续数学。花括号将此状态更改限制在封闭的片段内。例如，要仅对求和符号使用文本样式，您将输入

\begin{equation}
   C^i_j = {\textstyle \sum_k} A^i_k B^k_j
\end{equation}

与命令相同的是这样

\newcommand{\tsum}[1]{{\textstyle \sum_{#1}}}

注意额外的花括号。只在一组表达式周围是不够的。这将导致\tsum k之后的数学都以文本样式显示。

要以显示样式显示公式的一部分，请执行相同的操作，但使用\displaystyle代替。

高级数学：AMS 数学包

AMS（美国数学学会）数学包是一个强大的包，它在数学 LaTeX 语言之上创建了一个更高的抽象层；如果您使用它，它将使您的生活更轻松。一些命令amsmath引入将使其他纯 LaTeX 命令过时：为了保持最终输出的一致性，您最好在可能的情况下使用amsmath命令。如果您这样做，您将获得优雅的输出，而无需担心对齐和其他细节，使您的源代码可读。如果您想使用它，您需要在前言中添加以下内容

\usepackage{amsmath}

在公式中引入点

amsmath还定义了\dots命令，它是现有\ldots的泛化。您可以在文本和数学模式下使用\dots，LaTeX 将用三个点“…”替换它，但它将根据上下文决定是将其放在底部（如\ldots）还是居中（如\cdots）。

点

LaTeX 提供了几个命令，以便在您的公式中插入点（省略号）。如果您需要输入大型矩阵并省略元素，这将特别有用。首先，以下是 LaTeX 提供的主要与点相关的命令

代码	输出	注释
`\dots`	$\dots$	通用点（省略号），用于文本（也用于公式之外）。它根据上下文自动管理前后空格，这是一个更高层的命令。
`\ldots`	$\ldots$	输出类似于上一个，但没有自动空格管理；它在更低级别上工作。
`\cdots`	$\cdots$	这些点相对于字母的高度居中。还有二元乘法运算符`\cdot`，如下所述。
`\vdots`	$\vdots$	垂直点
`\ddots`	$\ddots$	对角点
`\iddots`		反向对角点（需要mathdots包）
`\hdotsfor{n}`	$\ldots \ldots$	用于矩阵中，它会创建跨越 n 列的一行点。

不要使用 \ldots 和 \cdots，而是使用语义导向的命令。这样可以根据需要动态调整您的文档以适应不同的约定，例如，如果您需要将文档提交给坚持遵循内部传统的出版商。

代码	输出	注释
`A_1,A_2,\dotsc,`		用于 "带逗号的点"
`A_1+\dotsb+A_N`		用于 "带二元运算符/关系的点"
`A_1 \dotsm A_N`		用于 "乘法点"
`\int_a^b \dotsi`		用于 "带积分的点"
`A_1\dotso A_N`		用于 "其他点"（不包括以上类型）

使用 align 环境编写方程式

如何在使用 amsmath 包的情况下，使用 align 环境编写方程式，请参见高级数学中的描述。

数学符号列表

以下是 \TeX\ 包中所有预定义的数学符号。更多符号可在其他包中获取。

关系符号
符号	脚本	符号	脚本	符号	脚本	符号	脚本	符号	脚本
$<\,$	`<`	$>\,$	`>`	$=\,$	`=`	$\parallel \,$	`\parallel`	$\nparallel \,$	`\nparallel`
$\leq \,$	`\leq`	$\geq \,$	`\geq`	$\doteq \,$	`\doteq`	$\asymp \,$	`\asymp`	$\bowtie \,$	`\bowtie`
$\ll \,$	`\ll`	$\gg \,$	`\gg`	$\equiv \,$	`\equiv`	$\vdash \,$	`\vdash`	$\dashv \,$	`\dashv`
$\subset \,$	`\subset`	$\supset \,$	`\supset`	$\approx \,$	`\approx`	$\in \,$	`\in`	$\ni \,$	`\ni`
$\subseteq \,$	`\subseteq`	$\supseteq \,$	`\supseteq`	$\cong \,$	`\cong`	$\smile \,$	`\smile`	$\frown \,$	`\frown`
$\nsubseteq \,$	`\nsubseteq`	$\nsupseteq \,$	`\nsupseteq`	$\simeq \,$	`\simeq`	$\models \,$	`\models`	$\notin \,$	`\notin`
$\sqsubset \,$	`\sqsubset`	$\sqsupset \,$	`\sqsupset`	$\sim \,$	`\sim`	$\perp \,$	`\perp`	$\mid \,$	`\mid`
$\sqsubseteq \,$	`\sqsubseteq`	$\sqsupseteq \,$	`\sqsupseteq`	$\propto \,$	`\propto`	$\prec \,$	`\prec`	$\succ \,$	`\succ`
$\preceq \,$	`\preceq`	$\succeq \,$	`\succeq`	$\neq \,$	`\neq`	$\sphericalangle \,$	`\sphericalangle`	$\measuredangle \,$	`\measuredangle`
$\therefore \,$	`\therefore`	$\because \,$	`\because`

二元运算
符号	脚本	符号	脚本	符号	脚本	符号	脚本
$\pm \,$	`\pm`	$\cap \,$	`\cap`	$\diamond \,$	`\diamond`	$\oplus \,$	`\oplus`
$\mp \,$	`\mp`	$\cup \,$	`\cup`	$\bigtriangleup \,$	`\bigtriangleup`	$\ominus \,$	`\ominus`
$\times \,$	`\times`	$\uplus \,$	`\uplus`	$\bigtriangledown \,$	`\bigtriangledown`	$\otimes \,$	`\otimes`
$\div \,$	`\div`	$\sqcap \,$	`\sqcap`	$\triangleleft \,$	`\triangleleft`	$\oslash \,$	`\oslash`
$\ast \,$	`\ast`	$\sqcup \,$	`\sqcup`	$\triangleright \,$	`\triangleright`	$\odot \,$	`\odot`
$\star \,$	`\star`	$\vee \,$	`\vee`	$\bigcirc \,$	`\bigcirc`	$\circ \,$	`\circ`
$\dagger \,$	`\dagger`	$\wedge \,$	`\wedge`	$\bullet \,$	`\bullet`	$\setminus \,$	`\setminus`
$\ddagger \,$	`\ddagger`	$\cdot \,$	`\cdot`	$\wr \,$	`\wr`	$\amalg \,$	`\amalg`

集合和/或逻辑符号
符号	脚本	符号	脚本
$\exists \,$	`\exists`	$\rightarrow \,$	`\rightarrow` 或 `\to`
$\nexists \,$	`\nexists`	$\leftarrow \,$	`\leftarrow` 或 `\gets`
$\forall \,$	`\forall`	$\mapsto \,$	`\mapsto`
$\neg \,$	`\neg`	$\implies \,$	`\implies`
$\cap$	`\cap`
$\cup$	`\cup`
$\subset \,$	`\subset`	⟸	`\impliedby`
$\supset \,$	`\supset`	$\Rightarrow \,$	`\Rightarrow` 或 `\implies`
$\in$	`\in`	$\leftrightarrow \,$	`\leftrightarrow`
$\notin \,$	`\notin`	$\iff \,$	`\iff`
$\ni \,$	`\ni`	$\Leftrightarrow \,$	`\Leftrightarrow` （等价（iff）的首选）
$\land \,$	`\land`	$\top \,$	`\top`
$\lor \,$	`\lor`	$\bot \,$	`\bot`
$\angle \,$	`\angle`	$\emptyset \,$ 和 $\varnothing \,$	`\emptyset` 和 `\varnothing`^[1]
		$\rightleftharpoons \,$	`\rightleftharpoons`

定界符
符号	脚本	符号	脚本	符号	脚本	符号	脚本
$\|\,$	`\|` 或 `\mid` (间距不同)	$\\|\,$	`\\|`	$/\,$	`/`	$\backslash \,$	`\backslash`
$\{\,$	`\{`	$\}\,$	`\}`	$\langle \,$	`\langle`	$\rangle \,$	`\rangle`
$\uparrow \,$	`\uparrow`	$\Uparrow \,$	`\Uparrow`	$\lceil \,$	`\lceil`	$\rceil \,$	`\rceil`
$\downarrow \,$	`\downarrow`	$\Downarrow \,$	`\Downarrow`	$\lfloor \,$	`\lfloor`	$\rfloor \,$	`\rfloor`

注意：在 LaTeX 中使用与拉丁字母外观相同的希腊字母，只需使用拉丁字母：例如，使用 A 而不是 Alpha，使用 B 而不是 Beta，等等。

希腊字母
符号	脚本	符号	脚本
$\mathrm {A} \,$ 和 $\alpha \,$	`A` 和 `\alpha`	$\mathrm {N} \,$ 和 $\nu \,$	`N` 和 `\nu`
$\mathrm {B} \,$ 和 $\beta \,$	`B` 和 `\beta`	$\Xi \,$ 和 $\xi \,$	`\Xi` 和 `\xi`
$\Gamma \,$ 和 $\gamma \,$	`\Gamma` 和 `\gamma`	$\mathrm {O} \,$ 和 $\mathrm {o} \,$	`O` 和 `o`
$\Delta \,$ 和 $\delta \,$	`\Delta` 和 `\delta`	$\Pi \,$ ， $\pi \,$ 和 $\varpi$	`\Pi`, `\pi` 和 `\varpi`
$\mathrm {E} \,$ ， $\epsilon \,$ 和 $\varepsilon \,$	`E`, `\epsilon` 和 `\varepsilon`	$\mathrm {P} \,$ , $\rho \,$ 和 $\varrho \,$	`P`、`\rho` 和 `\varrho`
$\mathrm {Z} \,$ 和 $\zeta \,$	`Z` 和 `\zeta`	$\Sigma \,$ , $\sigma \,$ 和 $\varsigma \,$	`\Sigma`、`\sigma` 和 `\varsigma`
$\mathrm {H} \,$ 和 $\eta \,$	`H` 和 `\eta`	$\mathrm {T} \,$ 和 $\tau \,$	`T` 和 `\tau`
$\Theta \,$ , $\theta \,$ 和 $\vartheta \,$	`\Theta`、`\theta` 和 `\vartheta`	${\mbox{Y}}\,$ , $\Upsilon \,$ 和 $\upsilon \,$	`Y`、`\Upsilon` 和 `\upsilon`
$\mathrm {I} \,$ 和 $\iota \,$	`I` 和 `\iota`	$\Phi \,$ , $\phi \,$ , 和 $\varphi \,$	`\Phi`, `\phi` 和 `\varphi`
$\mathrm {K} \,$ , $\kappa \,$ 和 $\varkappa \,$	`K`, `\kappa` 和 `\varkappa`	$\mathrm {X} \,$ 和 $\chi \,$	`X` 和 `\chi`
$\Lambda \,$ 和 $\lambda \,$	`\Lambda` 和 `\lambda`	$\Psi \,$ 和 $\psi \,$	`\Psi` 和 `\psi`
$\mathrm {M} \,$ 和 $\mu \,$	`M` 和 `\mu`	$\Omega \,$ 和 $\omega \,$	`\Omega` 和 `\omega`

其他符号
符号	脚本	符号	脚本	符号	脚本	符号	脚本	符号	脚本
$\partial \,$	`\partial`	$\imath \,$	`\imath`	$\Re \,$	`\Re`	$\nabla \,$	`\nabla`	$\aleph \,$	`\aleph`
$\eth \,$	`\eth`	$\jmath \,$	`\jmath`	$\Im \,$	`\Im`	$\Box \,$	`\Box`	$\beth \,$	`\beth`
$\hbar \,$	`\hbar`	$\ell \,$	`\ell`	$\wp \,$	`\wp`	$\infty \,$	`\infty`	$\gimel \,$	`\gimel`

^ 在 LaTeX 2 中未预定义。请使用 latexsym、amsfonts、amssymb、txfonts、pxfonts 或 wasysym 包中的一个。

三角函数
符号	脚本	符号	脚本	符号	脚本	符号	脚本
$\sin \,$	`\sin`	$\arcsin \,$	`\arcsin`	$\sinh \,$	`\sinh`	$\sec \,$	`\sec`
$\cos \,$	`\cos`	$\arccos \,$	`\arccos`	$\cosh \,$	`\cosh`	$\csc \,$	`\csc`
$\tan \,$	`\tan`	$\arctan \,$	`\arctan`	$\tanh \,$	`\tanh`
$\cot \,$	`\cot`	$\operatorname {arccot} \,$	`\arccot`	$\coth \,$	`\coth`

如果 LaTeX 不包含您想要使用的数学运算符的命令，例如 \cis（cosine 加上 i 乘以 sine），请在您的前言中添加

\DeclareMathOperator\cis{cis}

然后，您就可以像使用 \cos 或任何其他数学运算符一样在文档中使用 \cis。

摘要

正如您所见，排版数学公式有时会很棘手。但是，由于 LaTeX 提供了如此多的控制，您可以用相对较少的努力获得专业质量的数学排版（当然，在您练习了一段时间之后！）。由于可能性似乎无穷无尽，因此可以详细说明数学的细枝末节。但是，使用本教程，您应该能够足够地进行操作。

待办事项

从 [2] 介绍符号
从 [3] 添加符号
考虑从 [4] 添加符号 - 几乎所有可用于 LaTeX 的符号列表
考虑使用 [5] 中已介绍的内容，而不是使用上述提到的符号，而不是重新键入表格
如何在 align 环境中框定一个方程式
方程式中的颜色

参考文献

说明

↑ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l ^m ⁿ ^o ^p ^q ^r ^s ^t 需要 amsmath 包
↑ ^a ^b ^c ^d ^e ^f 需要 mathtools 包
↑ ^a ^b ^c ^d ^e ^f mathalpha 包允许指定在 \mathfrak{}、\mathbb{}、\mathcal{} 和 \mathscr{} 命令中使用的更广泛的字体。例如，命令 \usepackage[bb=pazo]{mathalpha} 使 \mathbb{} 使用 "pazo" 字体。 mathalpha 的文档对不同的字体选项进行了比较；其中一些具有默认情况下没有的小写字母、希腊字母或数字。

进一步阅读

meta:帮助：显示公式: 维基媒体使用 LaTeX 命令的子集。

外部链接

detexify: 通过绘制它们查找 LaTeX 符号的小程序
amsmath文档
LaTeX - 学生房间
LaTeX 符号列表
数学符号的完整列表

上一个：规则和撑杆

索引

下一个：高级数学

[1] ttp://www.ams.org/publications/authors/tex/amslatex

[2] ttp://www.ctan.org/tex-archive/macros/latex/contrib/mathtools/mathtools.pdf

[LM-4] ttp://hdl.handle.net/2268/6219

[amsmath-3] ↑ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l ^m ⁿ ^o ^p ^q ^r ^s ^t 需要 amsmath 包

[mathtools-5] ↑ ^a ^b ^c ^d ^e ^f 需要 mathtools 包

[mathalfa-6] ↑ ^a ^b ^c ^d ^e ^f mathalpha 包允许指定在 \mathfrak{}、\mathbb{}、\mathcal{} 和 \mathscr{} 命令中使用的更广泛的字体。例如，命令 \usepackage[bb=pazo]{mathalpha} 使 \mathbb{} 使用 "pazo" 字体。 mathalpha 的文档对不同的字体选项进行了比较；其中一些具有默认情况下没有的小写字母、希腊字母或数字。

[1]

[2]

[注 1]

[3]

[注 2]

[注 3]

[1]