算法

[编辑 | 编辑源代码]

后处理 = 图像修改 = 图形算法 = 图像处理

按图形类型分类的算法

光栅算法
矢量算法

五类图像处理算法

图像恢复
图像分析
图像合成
图像增强
图像压缩。

列表：^[1]^[2]^[3]

色彩理论：色彩渐变
二维平面变换
- 二维到三维^[4]
  - 高度图^[5]
  - 坡度

二值图像的形态学运算^[6]^[7]
- 形态学闭运算 = 膨胀后腐蚀
- 形态学开运算 = 腐蚀后膨胀

后处理

两种边缘检测类型
伪三维投影
星空场生成器
随机点立体图（又名魔眼）
动画的运动模糊
隔行扫描
浮雕
反锯齿
调色板模拟，允许真彩色显示器上的颜色循环
真彩色模拟，在 256 色显示器上提供抖动

算法

使用渐变映射，在分形创建后独立于分形创建进行着色
- 直方图着色
密集图像的伽马校正^[8]
维基百科中的直方图均衡
（矩阵）卷积（= 离散卷积）是两个矩阵的逐元素相乘，然后求和
- 图像卷积
  - LIC

类型

[编辑 | 编辑源代码]

范围

[编辑 | 编辑源代码]

图像处理运算符（算法）可以分为 4 类

像素算法 = 像素处理：点运算符作用于单个像素：g = H(f)
- 添加两张图像：g(x)=f1(x)+f2(x)
- 直方图
- 查找表（LUT）
- 窗口化
局部算法 = 核化 = 局部处理：“局部运算符计算像素值 g(x) 不仅基于输入图像中相同位置的值，即 f(x)，而且还使用附近点的几个值 f(x+y)。局部运算符是几乎所有图像处理任务的核心。”^[9]
- 空间位置滤波（卷积），
- 使用高通和低通数字滤波器的空间频率滤波，
- 反锐化遮罩技术^[10]
几何处理 = 几何变换：“虽然点运算符改变所有像素的值，但几何运算符不改变值，而是将像素‘移动’到新位置。”
全局运算符：“全局运算符（可能）需要输入图像中的所有像素值来计算输出图像中单个像素的值。”

库

[编辑 | 编辑源代码]

数字拓扑

[编辑 | 编辑源代码]

几何

[编辑 | 编辑源代码]

双曲
- 双曲

光

[编辑 | 编辑源代码]

光源

伽马校正

[编辑 | 编辑源代码]

gamma 校正 by Mikael Hvidtfeldt Christensen

密集图像

[编辑 | 编辑源代码]

密集图像^[11]^[12]^[13]^[14]^[15]

带 gamma 校正的降采样^[16]
路径查找^[17]
混叠 ^[18]
将算法（表示函数）从离散更改为连续，例如从逃逸时间水平集方法更改为连续（DEM）

  "the denser the area, the more heavy the anti-aliasing have to be in order to make it look good."  knighty^[19]

  "the details are smaller than pixel spacing, so all that remains is the bands of colour shift from period-doubling of features making it even denser"  claude^[20]

平铺

[编辑 | 编辑源代码]

平铺编辑器
Tiling Bot by Roice Nelson
绘制双曲平面中均匀平铺的 Wythoff 构造
EPINET = 非欧几里得平铺中的欧几里得模式

路径查找

[编辑 | 编辑源代码]

路径查找

算法^[21]

深度优先搜索 (DFS) = 最简单的算法
广度优先搜索 (BFS)
双向搜索
Dijkstra 算法（或 Dijkstra 最短路径优先算法，SPF 算法）
- programiz：dijkstra-algorithm
- dyclassroom：dijkstra-algorithm-finding-shortest-path
Bellman-Ford 算法

尺寸

[编辑 | 编辑源代码]

如何打开大图像
- vliv: Vliv 背后的原理（只加载可见的图像部分，并利用 TIFF 格式 - 平铺金字塔图像）可以在任何操作系统上实现。插件的 API 只有 5 个函数，请参阅 vlivplugins repo 以获取示例。

调整大小

[编辑 | 编辑源代码]

方法

Image Magic 调整大小
FF
2^x 图像超分辨率
- Final2x
- image-super-resolution

多边形

[编辑 | 编辑源代码]

二维多边形的几何运算^[22]^[23]

如何判断一个点位于直线的右侧还是左侧？

[编辑 | 编辑源代码]

/* 
  How to tell whether a point is to the right or left side of a line ?

 http://stackoverflow.com/questions/1560492/how-to-tell-whether-a-point-is-to-the-right-or-left-side-of-a-line

  a, b = points
  line = ab
 pont to check = z

  position = sign((Bx - Ax) * (Y - Ay) - (By - Ay) * (X - Ax))
  It is 0 on the line, and +1 on one side, -1 on the other side.

*/

double CheckSide(double Zx, double Zy, double Ax, double Ay, double Bx, double By)
{
  return ((Bx - Ax) * (Zy - Ay) - (By - Ay) * (Zx - Ax));

}

测试点是否在三角形内

[编辑 | 编辑源代码]

描述^[24]^[25]
javascript 代码 ^[26]

/* 
c console program 
gcc t.c -Wall
./a.out

*/

# include <stdio.h>

// 3 points define triangle 
double Zax = -0.250000000000000;
double Zay = 0.433012701892219;
// left when y
double Zlx = -0.112538773749444;  
double Zly = 0.436719687479814 ;

double Zrx = -0.335875821657728;
double Zry = 0.316782798339332;

// points to test 
// = inside triangle 
double Zx = -0.209881783739630;
double Zy =   +0.4;

// outside triangle 
double Zxo = -0.193503885412548  ;
double Zyo = 0.521747636163664;

double Zxo2 = -0.338750000000000;
double Zyo2 = +0.440690927838329;

// ============ http://stackoverflow.com/questions/2049582/how-to-determine-a-point-in-a-2d-triangle
// In general, the simplest (and quite optimal) algorithm is checking on which side of the half-plane created by the edges the point is.
double sign (double  x1, double y1,  double x2, double y2, double x3, double y3)
{
    return (x1 - x3) * (y2 - y3) - (x2 - x3) * (y1 - y3);
}

int  PointInTriangle (double x, double y, double x1, double y1, double x2, double y2, double x3, double y3)
{
    double  b1, b2, b3;

    b1 = sign(x, y, x1, y1, x2, y2) < 0.0;
    b2 = sign(x, y, x2, y2, x3, y3) < 0.0;
    b3 = sign(x, y, x3, y3, x1, y1) < 0.0;

    return ((b1 == b2) && (b2 == b3));
}

int Describe_Position(double Zx, double Zy){
if (PointInTriangle( Zx, Zy, Zax, Zay, Zlx, Zly, Zrx, Zry))
  printf(" Z is inside \n");
  else printf(" Z is outside \n");

return 0;
}

// ======================================

int main(void){

Describe_Position(Zx, Zy);
Describe_Position(Zxo, Zyo);
Describe_Position(Zxo2, Zyo2);

return 0;
}

三角形的朝向和面积

[编辑 | 编辑源代码]

三角形的朝向和面积：如何操作？

// gcc t.c -Wall
// ./a.out
# include <stdio.h>

// http://ncalculators.com/geometry/triangle-area-by-3-points.htm
double GiveTriangleArea(double xa, double ya, double xb, double yb, double xc, double yc)
{
return ((xb*ya-xa*yb)+(xc*yb-xb*yc)+(xa*yc-xc*ya))/2.0;
}

/*

wiki Curve_orientation
[http://mathoverflow.net/questions/44096/detecting-whether-directed-cycle-is-clockwise-or-counterclockwise]

The orientation of a triangle (clockwise/counterclockwise) is the sign of the determinant

matrix = { {1 , x1, y1}, {1 ,x2, y2} , {1,  x3, y3}}

where 
(x_1,y_1), (x_2,y_2), (x_3,y_3)$ 
are the Cartesian coordinates of the three vertices of the triangle.

:<math>\mathbf{O} = \begin{bmatrix}

1 & x_{A} & y_{A} \\
1 & x_{B} & y_{B} \\
1 & x_{C} & y_{C}\end{bmatrix}.</math>

A formula for its determinant may be obtained, e.g., using the method of [[cofactor expansion]]:
:<math>\begin{align}
\det(O) &= 1\begin{vmatrix}x_{B}&y_{B}\\x_{C}&y_{C}\end{vmatrix}
-x_{A}\begin{vmatrix}1&y_{B}\\1&y_{C}\end{vmatrix}
+y_{A}\begin{vmatrix}1&x_{B}\\1&x_{C}\end{vmatrix} \\
&= x_{B}y_{C}-y_{B}x_{C}-x_{A}y_{C}+x_{A}y_{B}+y_{A}x_{C}-y_{A}x_{B} \\
&= (x_{B}y_{C}+x_{A}y_{B}+y_{A}x_{C})-(y_{A}x_{B}+y_{B}x_{C}+x_{A}y_{C}).
\end{align}
</math>

If the determinant is negative, then the polygon is oriented clockwise.  If the determinant is positive, the polygon is oriented counterclockwise.  The determinant  is non-zero if points A, B, and C are non-[[collinear]].  In the above example, with points ordered A, B, C, etc., the determinant is negative, and therefore the polygon is clockwise.

*/

double IsTriangleCounterclockwise(double xa, double ya, double xb, double yb, double xc, double yc)
{return  ((xb*yc + xa*yb +ya*xc) - (ya*xb +yb*xc + xa*yc)); }

int DescribeTriangle(double xa, double ya, double xb, double yb, double xc, double yc)
{
 double t = IsTriangleCounterclockwise( xa,  ya, xb,  yb,  xc,  yc);
 double a = GiveTriangleArea( xa,  ya, xb,  yb,  xc,  yc);
 if (t>0)  printf("this triangle is oriented counterclockwise,     determinent = %f ; area = %f\n", t,a);
 if (t<0)  printf("this triangle is oriented clockwise,            determinent = %f; area = %f\n", t,a);
 if (t==0) printf("this triangle is degenerate: colinear or identical points, determinent = %f; area = %f\n", t,a);

 return 0;
}

int main()
{
 // clockwise oriented triangles 
 DescribeTriangle(-94,   0,  92,  68, 400, 180); // https://www-sop.inria.fr/prisme/fiches/Arithmetique/index.html.en
 DescribeTriangle(4.0, 1.0, 0.0, 9.0, 8.0, 3.0); // clockwise orientation https://people.sc.fsu.edu/~jburkardt/datasets/triangles/tex5.txt
 
 //  counterclockwise oriented triangles
 DescribeTriangle(-50.00, 0.00, 50.00,  0.00, 0.00,  0.02); // a "cap" triangle. This example has an area of 1.
 DescribeTriangle(0.0,  0.0, 3.0,  0.0, 0.0,  4.0); // a right triangle. This example has an area of (?? 3 ??)  =  6
 DescribeTriangle(4.0, 1.0, 8.0, 3.0, 0.0, 9.0);  //      https://people.sc.fsu.edu/~jburkardt/datasets/triangles/tex1.txt
 DescribeTriangle(-0.5, 0.0,  0.5,  0.0, 0.0,  0.866025403784439); // an equilateral triangle. This triangle has an area of sqrt(3)/4.

 // degenerate triangles 
 DescribeTriangle(1.0, 0.0, 2.0, 2.0, 3.0, 4.0); // This triangle is degenerate: 3 colinear points. https://people.sc.fsu.edu/~jburkardt/datasets/triangles/tex6.txt
 DescribeTriangle(4.0, 1.0, 0.0, 9.0, 4.0, 1.0); //2 identical points 
 DescribeTriangle(2.0, 3.0, 2.0, 3.0, 2.0, 3.0); // 3 identical points

 return 0; 
}

测试点是否在多边形内

[编辑 | 编辑源代码]

stackoverflow^[27]
由 W Muła 描述^[28]
point_in_polygon by Patrick Glauner
- 复杂多边形的点在多边形问题中一个简单且正确的奇偶算法 by Michael Galetzka, Patrick O. Glauner
- c 代码
PNPOLY - 点在多边形内测试 - W. Randolph Franklin (WRF)

/*

gcc p.c -Wall
./a.out

----------- git --------------------
cd existing_folder
git init
git remote add origin [email protected]:adammajewski/PointInPolygonTest_c.git
git add .
git commit
git push -u origin master

*/

#include <stdio.h>

#define LENGTH 6

/*

Argument	Meaning
nvert	Number of vertices in the polygon. Whether to repeat the first vertex at the end is discussed below.
vertx, verty	Arrays containing the x- and y-coordinates of the polygon's vertices.
testx, testy	X- and y-coordinate of the test point.

https://www.ecse.rpi.edu/Homepages/wrf/Research/Short_Notes/pnpoly.html
PNPOLY - Point Inclusion in Polygon Test
W. Randolph Franklin (WRF)

	

I run a semi-infinite ray horizontally (increasing x, fixed y) out from the test point, 
and count how many edges it crosses. 
At each crossing, the ray switches between inside and outside. 
This is called the Jordan curve theorem.
The case of the ray going thru a vertex is handled correctly via a careful selection of inequalities. 
Don't mess with this code unless you're familiar with the idea of Simulation of Simplicity. 
This pretends to shift the ray infinitesimally down so that it either clearly intersects, or clearly doesn't touch. 
Since this is merely a conceptual, infinitesimal, shift, it never creates an intersection that didn't exist before, 
and never destroys an intersection that clearly existed before.

The ray is tested against each edge thus:

Is the point in the half-plane to the left of the extended edge? and
Is the point's Y coordinate within the edge's Y-range?
Handling endpoints here is tricky.

I run a semi-infinite ray horizontally (increasing x, fixed y) out from the test point, 
and count how many edges it crosses. At each crossing, 
the ray switches between inside and outside. This is called the Jordan curve theorem.
The variable c is switching from 0 to 1 and 1 to 0 each time the horizontal ray crosses any edge. 
So basically it's keeping track of whether the number of edges crossed are even or odd. 
0 means even and 1 means odd.

*/

int pnpoly(int nvert, double *vertx, double *verty, double testx, double testy)
{
  int i, j, c = 0;
  for (i = 0, j = nvert-1; i < nvert; j = i++) {
    if ( ((verty[i]>testy) != (verty[j]>testy)) &&
	 (testx < (vertx[j]-vertx[i]) * (testy-verty[i]) / (verty[j]-verty[i]) + vertx[i]) )
       c = !c;
  }

  return c;
}

void CheckPoint(int nvert, double *vertx, double *verty, double testx, double testy){

int flag;

flag =  pnpoly(nvert, vertx, verty, testx, testy);

 switch(flag){
   case 0  : printf("outside\n"); break;
   case 1  : printf("inside\n"); break;
   default : printf(" ??? \n");
 }
}

int main (){

// values from http://stackoverflow.com/questions/217578/how-can-i-determine-whether-a-2d-point-is-within-a-polygon
// number from 0 to (LENGTH-1)
double zzx[LENGTH] = { 13.5,  6.0, 13.5, 42.5, 39.5, 42.5};
double zzy[LENGTH] = {100.0, 70.5, 41.5, 56.5, 69.5, 84.5};

CheckPoint(LENGTH, zzx, zzy, zzx[4]-0.001, zzy[4]);
CheckPoint(LENGTH, zzx, zzy, zzx[4]+0.001, zzy[4]);

return 0;
}

曲线

[编辑 | 编辑源代码]

类型

闭合/开放
带/不带多个点

方法

追踪/绘制：生成离散曲线
草绘
采样
路径查找或寻路是指计算机应用程序绘制两个点之间最短路线的过程
裁剪
数字化曲线的逼近（使用三次贝塞尔曲线）
曲线拟合^[29]
修复断线^[30]
边缘检测

示例

直线
- bresenhams-drawing-algorithms^[31]^[32]^[33]^[34]
- 反锯齿^[35]

圆形 ^[36]

莫顿码

[编辑 | 编辑源代码]

libmorton 带有方法的 C++ 纯头文件库，可有效地在 2D/3D 坐标中对莫顿码进行编码/解码
aavenel mortonlib

变形

[编辑 | 编辑源代码]

p5.js 中从圆形到三角形的插值 by Golan Levin

曲线简化

[编辑 | 编辑源代码]

减少点数，但仍保持曲线的整体形状 = 折线缩减

曲线拟合

[编辑 | 编辑源代码]

我的曲线拟合：在线曲线拟合

粗线绘制

[编辑 | 编辑源代码]

粗线

曲线绘制

[编辑 | 编辑源代码]

用于光栅显示的曲线绘制算法，作者：JERRY VAN AKEN 和 MARK NOVAK
用于绘制曲线的栅格化算法，作者：Alois Zingl Wien，2012 年
用于光栅显示的曲线绘制算法，作者：JERRY VAN AKEN 和 MARK NOVAK
A* 路径查找入门，作者：Patrick Lester（更新于 2005 年 7 月 18 日）
Max K. Agoston 计算机图形学与几何建模：实现与算法
libspiro 是 Raph Levien 的作品。它简化了绘制美丽曲线的过程。
spiro 基于螺旋线的插值样条曲线

2D 算法的邻域变体

8 向步进 (8WS) 用于像素 p(x, y) 的 8 个方向邻居
4 向步进 (4WS) 用于像素 p(x, y) 的 4 个方向邻居

2D 邻域
4
8

曲线采样

[编辑 | 编辑源代码]

均匀 = 给出等距点
自适应。“一种自适应方法，用于根据局部曲率对域进行采样。采样集中度与该曲率成正比，从而产生更有效的近似——极限情况下，一条平坦曲线仅用两个端点来近似。” ^[38]

场线

[编辑 | 编辑源代码]

场线^[39]

追踪

[编辑 | 编辑源代码]

追踪曲线^[40]

方法

一般，（解析或系统化） = 曲线绘制^[41]
局部方法

任务：绘制 2D 曲线，当

没有直线方程
直线在一定范围内所有数值

追踪角度为 t（以圈为单位）的外射线，这意味着（Claude Heiland-Allen 描述）^[42]

从一个大圆圈开始（例如，r = 65536，x = r cos(2 pi t)，y = r sin(2 pi t)）
沿着逃逸线（如使用大逃逸半径的二进制分解着色边的边缘）向曼德勃罗集内部移动。

此算法为 O(period^2)，这意味着周期加倍需要 4 倍的时间，因此它仅适用于周期不超过几千的算法。

三种曲线追踪模型^[43]

逐像素追踪
暴力法^[44]: 如果您的直线足够短（小于 10^6 个点），您可以通过计算点 p 到离散直线上每个点的距离来实现，并取这些距离的最小值。
二分感受野算子
变焦镜头算子

图像

commons 中曲线追踪类别下的图像

问题

交集和广度优先搜索^[45]

示例

向量场中粒子追踪的数值方法，作者：Kenneth I. Joy

曲线栅格化

[编辑 | 编辑源代码]

射线

[编辑 | 编辑源代码]

射线可以使用半径 (r) 进行参数化

闭合曲线

[编辑 | 编辑源代码]

简单闭合曲线（“一条连接的曲线，它不与自身相交，并且在开始点结束”^[46] = 没有端点）可以使用角度 (t) 进行参数化。

边界、轮廓、边缘

[编辑 | 编辑源代码]

填充轮廓
在二进制图像中查找轮廓
CavalierContoursWebDemo 以及代码

轮廓模型

[编辑 | 编辑源代码]

蛇形线 = 活动轮廓模型^[47]

边界追踪

[编辑 | 编辑源代码]

轮廓追踪算法，作者：Abeer George Ghuneim
二维图像中的边界追踪，作者：V. Kovalevsky^[48]
维基百科 : 边界追踪
计算二维标量场的轮廓曲线
- 用于追踪标量二维场上的轮廓曲线的游走方块算法^[49]
平滑轮廓^[50]
轮廓多边形^[51]
boundary in C++ by Shawn Halayka - 2019 and new code
opencv_contour in C++ by Shawn Halayka
CONREC，由 Paul Bourke 于 1987 年 7 月编写的轮廓子例程（使用三角测量）

填充轮廓

[编辑 | 编辑源代码]

填充轮廓 - c语言中的简单过程

边缘检测

[编辑 | 编辑源代码]

等高线 - 边缘检测（2 个滤波器）
逃逸时间等值面的边界边缘检测

Sobel 滤波器

[编辑 | 编辑源代码]

简要介绍

[编辑 | 编辑源代码]

Sobel 滤波器 G 由 2 个核（掩码）组成

Gh 用于水平变化。
Gv 用于垂直变化。

Sobel 核

[编辑 | 编辑源代码]

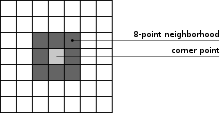
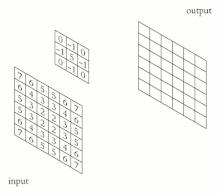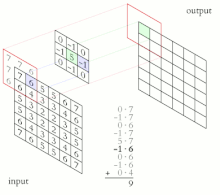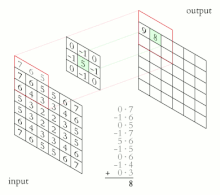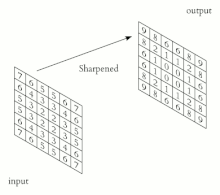
Sobel 核包含来自测试像素的 8 点邻域中每个像素的权重。这些是 3x3 核。

有两个 Sobel 核，一个用于计算水平变化，另一个用于计算垂直变化。请注意，大的水平变化可能表明垂直边界，而大的垂直变化可能表明水平边界。这里的 x 坐标定义为在“向右”方向上增加，y 坐标定义为在“向下”方向上增加。

用于计算水平变化的 Sobel 核为

\mathbf {H} ={\begin{bmatrix}H_{1}&H_{2}&H_{3}\\H_{4}&H_{5}&H_{6}\\H_{7}&H_{8}&H_{9}\end{bmatrix}}={\begin{bmatrix}-1&0&+1\\-2&0&+2\\-1&0&+1\end{bmatrix}}

用于计算垂直变化的 Sobel 核为

\mathbf {V} ={\begin{bmatrix}-1&-2&-1\\\ \ 0&\ \ 0&\ \ 0\\+1&+2&+1\end{bmatrix}}

请注意

内核的权重总和为零

$\sum _{i=1}^{9}H_{i}=0$

$\sum _{i=1}^{9}V_{i}=0$

一个内核只是另一个内核旋转 90 度。^[53]
每个内核中的 3 个权重为零。

像素内核

[编辑 | 编辑源代码]

包含中心像素 $A_{5}$ 及其 3x3 邻域的像素内核 A

\mathbf {A} ={\begin{bmatrix}A_{1}&A_{2}&A_{3}\\A_{4}&A_{5}&A_{6}\\A_{7}&A_{8}&A_{9}\end{bmatrix}}

像素内核的其他符号

\mathbf {A} ={\begin{bmatrix}A_{1}&A_{2}&A_{3}\\A_{4}&A_{5}&A_{6}\\A_{7}&A_{8}&A_{9}\end{bmatrix}}={\begin{bmatrix}ul&um&ur\\ml&mm&mr\\ll&lm&lr\end{bmatrix}}

其中：^[54]

unsigned char ul, // upper left
unsigned char um, // upper middle
unsigned char ur, // upper right
unsigned char ml, // middle left
unsigned char mm, // middle = central pixel
unsigned char mr, // middle right
unsigned char ll, // lower left
unsigned char lm, // lower middle
unsigned char lr, // lower right

在数组表示法中，它是：^[55]

\mathbf {A} ={\begin{bmatrix}A[x-1][y+1]&A[x][y+1]&A[x+1][y+1]\\A[x-1][y]&A[x][y]&A[x+1][y]\\A[x-1][y-1]&A[x][y-1]&A[x+1][y-1]\end{bmatrix}}

在细胞自动机中使用的地理表示法中，它是 Moore 邻域的中心像素。^{[check spelling]}

因此，中心（测试）像素是

$A_{5}=mm=A[x][y]\,$

Sobel 滤波器

[edit | edit source]

计算 Sobel 滤波器（其中 $*$ 表示二维卷积运算，而不是矩阵乘法）。它是像素及其权重的乘积之和

\mathbf {G} _{h}=\mathbf {H} *A=A_{1}H_{1}+A_{2}H_{2}+\cdots +A_{9}H_{9}=\sum _{r=1}^{9}A_{r}H_{r},

\mathbf {G} _{v}=\mathbf {V} *A=A_{1}V_{1}+A_{2}V_{2}+\cdots +A_{9}V_{9}=\sum _{r=1}^{9}A_{r}V_{r},

因为每个内核中的 3 个权重为零，所以只有 6 个乘积。^[56]

short Gh = ur + 2*mr + lr - ul - 2*ml - ll;
short Gv = ul + 2*um + ur - ll - 2*lm - lr;

结果

[edit | edit source]

计算结果（梯度大小）

\mathbf {G} (A_{5})={\sqrt {{\mathbf {G} _{h}}^{2}+{\mathbf {G} _{v}}^{2}}}

它是测试像素的颜色。

还可以通过两个幅度之和来近似结果

\mathbf {G} (A_{5})=\left|\mathbf {G} _{h}\right|+\left|\mathbf {G} _{v}\right|

这比计算快得多。^[57]

算法

[edit | edit source]

选择像素及其 3x3 邻域 A
计算水平 Gh 和垂直 Gv 的 Sobel 滤波器
计算 Sobel 滤波器 G
计算像素的颜色

编程

[edit | edit source]

我们来取一个称为 data 的 8 位颜色数组 (图像)。要在这个图像中找到边界，只需执行以下操作

for(iY=1;iY<iYmax-1;++iY){ 
    for(iX=1;iX<iXmax-1;++iX){ 
     Gv= - data[iY-1][iX-1] - 2*data[iY-1][iX] - data[iY-1][iX+1] + data[iY+1][iX-1] + 2*data[iY+1][iX] + data[iY+1][iX+1];
     Gh= - data[iY+1][iX-1] + data[iY-1][iX+1] - 2*data[iY][iX-1] + 2*data[iY][iX+1] - data[iY-1][iX-1] + data[iY+1][iX+1];
     G = sqrt(Gh*Gh + Gv*Gv);
     if (G==0) {edge[iY][iX]=255;} /* background */
         else {edge[iY][iX]=0;}  /* boundary */
    }
  }

注意，这里跳过了数组边界上的点 (iY= 0, iY = iYmax, iX=0, iX=iXmax)

结果保存到另一个称为 edge 的数组 (大小相同) 中。

可以将 edge 数组保存到文件中，只显示边界，或者合并 2 个数组

for(iY=1;iY<iYmax-1;++iY){ 
    for(iX=1;iX<iXmax-1;++iX){ if (edge[iY][iX]==0) data[iY][iX]=0;}}

以生成一个新的带有标记边界的图像。

上面的示例适用于 8 位或索引颜色。对于更高位的颜色，“公式分别应用于所有三个颜色通道”(来自 RoboRealm 文档)。

其他实现

问题

[edit | edit source]

在图像中间看到糟糕的边缘位置。线条没有在好的点相遇，例如 z = 0

边缘位置:

在 ImageMagick 中，正如“您所看到的，边缘只添加到颜色梯度大于 50% 白色的区域！我不知道这是错误还是有意为之，但这意味着上面边缘的位置几乎完全位于原始掩码图像的白色部分。这个事实对于使用“-edge”运算符的结果非常重要。”^[58]

结果是

边缘加倍；“如果你要对包含黑色轮廓的图像进行边缘检测，“-edge”运算符会‘双重’黑色线条，产生奇怪的结果。”^[59]
线条没有在好的点相遇。

另请参阅 ImageMagick 第 6 版中的新运算符：EdgeIn 和 EdgeOut，来自形态学^[60]

边缘加厚

[edit | edit source]

膨胀^[61]^[62]^[63]

convert $tmp0 -convolve "1,1,1,1,1,1,1,1,1" -threshold 0 $outfile

SDF 签名距离函数

[edit | edit source]

向量场 SDF

测试 2 个圆的外切

[edit | edit source]

/*
 distance between 2 points 
  z1 = x1 + y1*I
  z2 = x2 + y2*I
  en.wikipedia.org/wiki/Distance#Geometry
 
*/ 
 
double GiveDistance(int x1, int y1, int x2, int y2){
  return sqrt((x1-x2)*(x1-x2) + (y1-y2)*(y1-y2));
}

/*
mutually and externally tangent circles
mathworld.wolfram.com/TangentCircles.html
Two circles are mutually and externally tangent if distance between their centers is equal to the sum of their radii

*/

double TestTangency(int x1, int y1, int r1, int x2, int y2, int r2){
  double distance;

  distance = GiveDistance(x1, y1, x2, y2);
  return ( distance - (r1+r2));
// return should be zero
}

地图投影

[edit | edit source]

立体投影

[edit | edit source]

立体投影是从球体的北极 N 到球体南极 S 的切平面上点 P' 上的球体表面上点 P 的投影得到的映射投影。^[64]

将北极 N 设为标准单位向量 (0, 0, 1)，并将球体中心设为原点，这样南极处的切平面就有方程 z = 1。给定单位球体上的一个点 P = (x, y, z)，该点不是北极，它的像等于^[65]

 $P'=f(P)=({\frac {2x}{1-z}},{\frac {2y}{1-z}})=(u,v)$

平面上的笛卡尔网格在球体上看起来是扭曲的。网格线仍然垂直，但网格正方形的面积随着它们接近北极而减小。
平面上的极坐标网格在球体上看起来是扭曲的。网格曲线仍然垂直，但网格扇区的面积随着它们接近北极而减小

圆柱形

[edit | edit source]

Cylindrical projections in general have an increased vertical stretching as one moves towards either of the poles. Indeed, the poles themselves can't be represented (except at infinity). This stretching is reduced in the  Mercator projection by the natural logarithm scaling. ^[66]

墨卡托投影

[edit | edit source]

共形
圆柱形 = 墨卡托投影从球体映射到圆柱体。圆柱体沿 y 轴切割并展开。它在两个 y 方向上都给出了无限范围的矩形（参见截断）

圆柱形
标准墨卡托 (圆柱形)
墨卡托投影比较

标准墨卡托投影的两种等效构造

从球体到圆柱体 (一步)
2 步
- 使用标准立体投影将球体投影到一个中间 (立体) 平面，该投影是共形的
- 通过将立体平面等同于复平面 (该平面在复对数函数下的像，该函数除了原点（带有一个分支割线）以外都是共形的，

复对数 f(z) = ln(z)。实际上，极坐标为 (ρ,θ) 的复数 z 被映射到 f(z) = ln(ρ) + iθ。这会产生一个水平条带，

然后旋转 90° 后得到标准垂直墨卡托映射，或者等效地，f(z) 可以定义为 f(z) = i*ln(z)。

	正墨卡托		横墨卡托
		\

拉伸

[edit | edit source]

Cylindrical projections in general have an increased vertical stretching as one moves towards either of the poles. Indeed, the poles themselves can't be represented (except at infinity). This stretching is reduced in the  Mercator projection by the natural logarithm scaling. ^[67]

截断

[edit | edit source]

圆柱体不是无限的，因此墨卡托投影在球体两极产生越来越扭曲的无限条带。因此，墨卡托投影的坐标 y 在两极处变为无穷大，并且地图必须在小于 90 度的某个纬度处被截断（裁剪）。

这不必对称地进行

墨卡托的原始地图被截断在北纬 80° 和南纬 66°，结果是欧洲国家被移到了地图的中心。

地球的几何形状

[edit | edit source]

地球作为球体

地球地理坐标系 $(\phi ,\lambda )$

纬度是指地球或其他天体表面上一点的南北位置的坐标。纬度通常用角度表示，范围从南极的 –90° 到北极的 90°，赤道为 0°。纬度通常用希腊字母 phi ( $ϕ$ 或 $φ$ ) 表示。纬度以度、分、秒或十进制度为单位，以赤道为基准，分别向南北方向测量。
经度是指地球表面上一点的东-西位置的地理坐标。经度通常用角度测量，通常以度为单位，用希腊字母 lambda (λ) 表示。

从球体模型上看，地球显示了纬度 ( $\phi$ ) 和经度 ( $\lambda$ ) 的定义。网格间距为 10 度。

方程

[编辑 | 编辑源代码]

一步法

考虑一个半径为 R、经度为 λ、纬度为 φ 的地球上的点。λ₀ 的值为任意中心子午线的经度，通常但并非总是格林尼治子午线（即零度经线）。角度 λ 和 φ 以弧度表示。

将单位球面上的点 P $P=(R,\lambda ,\varphi )$ 映射到笛卡尔平面上的点 $Q=(x,y)$

{\begin{matrix}x=R(\lambda -\lambda _{0})\\y=R\ln \left[\tan \left({\frac {\pi }{4}}+{\frac {\varphi }{2}}\right)\right]\end{matrix}}

两步法

立体投影
复对数

立体投影的球面形式通常用极坐标表示

{\begin{matrix}r&=2R\tan \left({\frac {\pi }{4}}-{\frac {\varphi }{2}}\right)\\\theta &=\lambda \end{matrix}}

其中 $R$ 是球体的半径， $\varphi$ 和 $\lambda$ 分别是纬度和经度。

直角坐标

假设：A、B、C 和 D 是实数，使得 $A^{2}+B^{2}+C^{2}\neq 0$ .

定义

$\Sigma$ 定义为欧几里德空间中的单位球面，即

   $\Sigma :={\big \{}(x,y,z)\in \mathbb {R} ^{3}:x^{2}+y^{2}+z^{2}=1{\big \}}.$

$N$ 定义为单位球体的北极，即 $N:=(0,0,1)$ .
$S$ 定义为立体投影，即函数 $S:\Sigma \setminus \{N\}\rightarrow \mathbb {R} ^{2}$ 满足

   $Q=S{\big (}(x,y,z){\big )}={\Big (}{\frac {x}{1-z}},{\frac {y}{1-z}}{\Big )}$

对于每一个 $(x,y,z)\in \Sigma \setminus \{N\}$ .

圆柱坐标

圆柱坐标 (轴向半径 ρ, 方位角 φ, 高度 z) 可以通过以下公式转换为球坐标 (中心半径 r, 倾角 θ, 方位角 φ)

${\begin{aligned}r&={\sqrt {\rho ^{2}+z^{2}}},\\\theta &=\arctan {\frac {\rho }{z}}=\arccos {\frac {z}{\sqrt {\rho ^{2}+z^{2}}}},\\\varphi &=\varphi .\end{aligned}}$

反之，球坐标可以通过以下公式转换为圆柱坐标

${\begin{aligned}\rho &=r\sin \theta ,\\\varphi &=\varphi ,\\z&=r\cos \theta .\end{aligned}}$

这些公式假设两个系统具有相同的原点和相同的参考平面，以相同的方式从相同的轴测量方位角 $φ$ ，并且球面角 $θ$ 是从圆柱形 $z$ 轴的倾角。

代码

chinhsuanwu: 360-converter (一个 C/C++ 的 360 图像转换工具包)

信号处理

[edit | edit source]

线性连续时间滤波器

频率响应可以被分为多个不同的带形，描述了滤波器允许通过的频率频段（通带）和滤波器拒绝的频率（阻带）
- 低通滤波器 – 通过低频，衰减高频。
- 高通滤波器 – 通过高频，衰减低频。
- 带通滤波器 – 只允许通过某个频率范围内的频率。
- 带阻滤波器或带陷滤波器 – 只衰减某个频率范围内的频率。
- 陷波滤波器 – 只拒绝一个特定频率 - 一种极端的带阻滤波器。
- 梳状滤波器 – 具有多个规则间隔的窄通带，使带形呈现梳状外观。
- 全通滤波器 – 所有频率都通过，但输出的相位会发生改变。
截止频率是滤波器不再通过信号的频率。它通常在特定的衰减值（如 3 dB）下测量。
滚降是超过截止频率后衰减增大的速率。
过渡带，通带和阻带之间的（通常很窄）频率范围。
纹波是滤波器在通带内的插入损耗的变化。
滤波器的阶数是逼近多项式的次数，在无源滤波器中对应于构建它所需的元件数量。增加阶数会增加滚降，并使滤波器更接近理想响应。