控制系统/变换

变换

在本教材中，我们将讨论许多变换，并假定读者对此至少有一定的先验知识。本教材并非旨在向完全没有接触过变换的读者教授变换主题。然而，我们将在这里提供一个简短的复习，以帮助那些可能不太记得这个主题的人重新熟悉。如果你还不了解**拉普拉斯变换**或**傅里叶变换**，强烈建议你使用此页面作为简单指南，并在其他资源上查找信息。具体来说，维基百科 上有许多关于这些主题的信息。

变换基础

**变换**是一种数学工具，它将一个变量（或一组变量）中的方程转换为一个新变量（或一组新变量）。为此，变换必须去除所有“域变量”的实例，并添加一个新的“范围变量”。积分是变换的绝佳选择，因为定积分的极限将被代入域变量，并且该变量的所有实例都将从方程中移除。从域变量 *a* 转换为范围变量 *b* 的积分变换通常会以以下格式进行

${\mathcal {T}}[f(a)]=F(b)=\int _{C}f(a)g(a,b)da$

其中函数 *f(a)* 是要变换的函数，*g(a,b)* 被称为变换的**核**。通常，各种积分变换之间唯一的区别在于核。

拉普拉斯变换

可以使用以下 MATLAB 命令执行此操作

laplace

**拉普拉斯变换**将方程从时域转换为所谓的“S 域”、“拉普拉斯域”或“复域”。这些都是同一个数学空间的不同名称，在本教材和其他关于该主题的书籍中可能会互换使用。变换只能在以下条件下应用

1. 所讨论的系统或信号是模拟的。
2. 所讨论的系统或信号是线性的。
3. 所讨论的系统或信号是时不变的。
4. 所讨论的系统或信号是因果的。

变换定义如下

[拉普拉斯变换]

${\begin{matrix}F(s)={\mathcal {L}}[f(t)]=\int _{0}^{\infty }f(t)e^{-st}dt\end{matrix}}$

拉普拉斯变换的结果已被广泛地制表。关于拉普拉斯变换的更多信息，包括变换表，可以在附录 中找到。

如果我们有一个时域中的线性微分方程

${\begin{matrix}y(t)=ax(t)+bx'(t)+cx''(t)\end{matrix}}$

在初始条件为零的情况下，我们可以对方程进行拉普拉斯变换，如下所示

${\begin{matrix}Y(s)=aX(s)+bsX(s)+cs^{2}X(s)\end{matrix}}$

然后分离，得到

${\begin{matrix}Y(s)=X(s)[a+bs+cs^{2}]\end{matrix}}$

拉普拉斯逆变换

可以使用以下 MATLAB 命令执行此操作

ilaplace

**拉普拉斯逆变换**定义如下

[拉普拉斯逆变换]

${\begin{matrix}f(t)={\mathcal {L}}^{-1}\left\{F(s)\right\}={1 \over {2\pi i}}\int _{c-i\infty }^{c+i\infty }e^{st}F(s)\,ds\end{matrix}}$

逆变换将函数从拉普拉斯域转换回时域。

矩阵和向量

拉普拉斯变换可以以一种直观的方式用于线性方程组。假设我们有一组线性方程

${\begin{matrix}y_{1}(t)=a_{1}x_{1}(t)\end{matrix}}$

${\begin{matrix}y_{2}(t)=a_{2}x_{2}(t)\end{matrix}}$

我们可以将这些方程排列成矩阵形式，如下所示

${\begin{bmatrix}y_{1}(t)\\y_{2}(t)\end{bmatrix}}={\begin{bmatrix}a_{1}&0\\0&a_{2}\end{bmatrix}}{\begin{bmatrix}x_{1}(t)\\x_{2}(t)\end{bmatrix}}$

并用符号表示为

$\mathbf {y} (t)=A\mathbf {x} (t)$

我们可以对两边进行拉普拉斯变换

${\mathcal {L}}[\mathbf {y} (t)]=\mathbf {Y} (s)={\mathcal {L}}[A\mathbf {x} (t)]=A{\mathcal {L}}[\mathbf {x} (t)]=A\mathbf {X} (s)$

这与对方程组中的每个单独方程进行变换相同。

示例：RL 电路

有关电路的更多信息，请参阅
电路理论

在这里，我们将展示一个常见的一阶系统示例，即RL 电路。在电感器中，电流 I 和电压 V 之间的关系在时域中表示为导数

$V(t)=L{\frac {dI(t)}{dt}}$

其中 L 是一个称为“电感”的特殊量，它是电感器的属性。

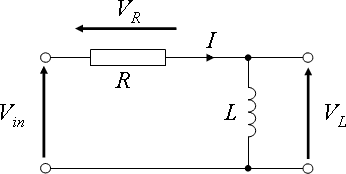RL 电路示例问题的电路图。V_L 是电感器上的电压，是我们试图找到的量。

假设我们有一个一阶 RL 串联电路。电阻的阻值为 R，电感器的电感值为 L，电压源的输入电压为 V_in。我们的电路的系统输出是电感器上的电压，V_out。在时域中，我们有以下一阶微分方程来描述电路

$V_{out}(t)=V_{L}(t)=L{\frac {dI(t)}{dt}}$

$V_{in}(t)=RI(t)+L{\frac {dI(t)}{dt}}$

然而，由于电路本质上充当分压器，我们可以将输出表示为输入的函数，如下所示

$V_{out}(t)={\frac {L{\frac {dI(t)}{dt}}}{RI(t)+L{\frac {dI(t)}{dt}}}}V_{in}(t)$

这是一个非常复杂的方程式，除非我们使用拉普拉斯变换，否则很难求解

$V_{out}(s)={\frac {Ls}{R+Ls}}V_{in}(s)$

我们可以将分子和分母都除以 L，并将 V_in 移到另一边

${\frac {V_{out}}{V_{in}}}={\frac {s}{{\frac {R}{L}}+s}}$

并使用简单的表格查找，我们可以求解电路输入和输出之间的时间域关系

${\frac {V_{out}}{V_{in}}}={\frac {d}{dt}}e^{\left({\frac {-Rt}{L}}\right)}u(t)$

部分分式展开

有关部分分式展开的更多信息，请参见
微积分

拉普拉斯变换对被广泛地列成表格，但我们经常会遇到没有列成表格的逆变换的传递函数和其他方程。如果我们的方程是一个分数，我们通常可以使用部分分式展开（PFE）来创建一组更简单的项，这些项将具有现成的逆变换。本节将简要回顾一下部分分式展开，供已经学过该主题的人参考。这个复习将以几个关于拉普拉斯变换的示例形式呈现。不熟悉部分分式展开的人建议阅读微积分了解更多信息。

示例：二阶系统

如果我们有 S 域中的给定方程

$F(s)={\frac {2s+1}{s^{2}+3s+2}}$

我们可以将其扩展成几个更小的分数，如下所示

$F(s)={\frac {2s+1}{(s+1)(s+2)}}={\frac {A}{(s+1)}}+{\frac {B}{(s+2)}}={\frac {A(s+2)+B(s+1)}{(s+1)(s+2)}}$

这看起来不可能，因为我们只有一个方程，有 3 个未知数（s、A、B），但实际上 s 可以取任何任意值，我们可以“代入”s 的值来求解 A 和 B，而不需要其他方程。例如，在上面的方程中，我们可以乘以分母，并消去项

${\frac {}{}}(2s+1)=A(s+2)+B(s+1)$

现在，当我们设置 s → -2 时，A 项消失，只剩下 B → 3。当我们设置 s → -1 时，我们可以求解 A → -1。将这些值代回原始方程，我们有

$F(s)={\frac {-1}{(s+1)}}+{\frac {3}{(s+2)}}$

请记住，由于拉普拉斯变换是线性算子，因此以下关系成立

${\mathcal {L}}^{-1}[F(s)]={\mathcal {L}}^{-1}\left[{\frac {-1}{(s+1)}}+{\frac {3}{(s+2)}}\right]={\mathcal {L}}^{-1}\left[{\frac {-1}{s+1}}\right]+{\mathcal {L}}^{-1}\left[{\frac {3}{(s+2)}}\right]$

寻找这些较小项的逆变换应该比寻找整个函数的逆变换更容易。部分分式展开是寻找 S 域方程的逆变换的一个有用且通常是必要的工具。

示例：四阶系统

如果我们有 S 域中的给定方程

$F(s)={\frac {79s^{2}+916s+1000}{s(s+10)^{3}}}$

我们可以将其扩展成几个更小的分数，如下所示

$F(s)={\frac {A}{s}}+{\frac {B}{(s+10)^{3}}}+{\frac {C}{(s+10)^{2}}}+{\frac {D}{s+10}}$

$F(s)={\frac {A(s+10)^{3}+Bs+Cs(s+10)+Ds(s+10)^{2}}{s(s+10)^{3}}}$

${\frac {}{}}A(s+10)^{3}+Bs+Cs(s+10)+Ds(s+10)^{2}=79s^{2}+916s+1000$

这里仅取消项是不够的，我们将展开括号（分隔成多行）

$As^{3}+30As^{2}+300As+1000A+Bs+$

$Cs^{2}+10Cs+Ds^{3}+20Ds^{2}+100Ds$

$=79s^{2}+916s+1000$

让我们比较系数

A + D = 0

30A + C + 20D = 79

300A + B + 10C + 100D = 916

1000A = 1000

解得

A = 1

B = 26

C = 69

D = -1

我们从拉普拉斯变换表中知道以下关系成立

${\frac {1}{(s+\alpha )^{n+1}}}\to {\frac {t^{n}}{n!}}e^{-\alpha t}\cdot u(t)$

我们可以将我们为 *A*、*B*、*C* 和 *D* 求得的值代入我们的展开式，并尝试将其转换为上面的形式。

$F(s)={\frac {A}{s}}+{\frac {B}{(s+10)^{3}}}+{\frac {C}{(s+10)^{2}}}+{\frac {D}{s+10}}$

$F(s)=A{\frac {1}{s}}+B{\frac {1}{(s+10)^{3}}}+C{\frac {1}{(s+10)^{2}}}+D{\frac {1}{s+10}}$

$F(s)=1{\frac {1}{s}}+26{\frac {1}{(s+10)^{3}}}+69{\frac {1}{(s+10)^{2}}}-1{\frac {1}{s+10}}$

$f(t)=u(t)+13t^{2}e^{-10t}+69te^{-10t}-e^{-10t}$

示例：复根

给定以下传递函数

$F(s)={\frac {7s+26}{s^{2}-80s+1681}}={\frac {As+B}{s^{2}-80s+1681}}$

当分母的解为复数时，我们使用复数表示A + iB，例如3+i4，而不是使用单个字母（例如D）——这是针对实数的。

As + B = 7s + 26

A = 7

B = 26

我们需要将其重构成两个类似于此形式的分数（不改变其值）

$e^{-\alpha t}\sin(\omega t)\cdot u(t)\$→${\omega \over (s+\alpha )^{2}+\omega ^{2}}$

$e^{-\alpha t}\cos(\omega t)\cdot u(t)\$→${s+\alpha \over (s+\alpha )^{2}+\omega ^{2}}$

让我们从分母开始（对于两个分数）

s² - 80s + 1681 的根是40 + j9 和40 - j9。

$(s+a)^{2}+\omega ^{2}=(s-40)^{2}+9^{2}$→${\frac {As+B}{(s-40)^{2}+9^{2}}}$

现在是分子

${\frac {As+40A-40A+B}{(s-40)^{2}+9^{2}}}$

${\frac {As-40A}{(s-40)^{2}+9^{2}}}+{\frac {B+40A}{(s-40)^{2}+9^{2}}}$

$A{\frac {(s-40)}{(s-40)^{2}+9^{2}}}+{\frac {B+40A}{9}}{\frac {9}{(s-40)^{2}+9^{2}}}$

拉普拉斯逆变换

$f(t)=7e^{40t}cos(9t)+34e^{40t}sin(9t)$

示例：六阶系统

给定以下传递函数

$F(s)={\frac {90s^{2}-1110}{s(s-3)(s^{2}-12s+37)}}={\frac {A}{s}}+{\frac {B}{s-3}}+{\frac {Cs+D}{s^{2}-12s+37}}$

我们将方程两边乘以分母，使其成为有理式

$A(s-3)(s^{2}-12s+37)+Bs(s^{2}-12s+37)+(Cs+D)s(s-3)$

$=90s^{2}-1110$

然后我们合并同类项

$As^{3}-15As^{2}+73As-111A+Bs^{3}-12Bs^{2}+37Bs+Cs^{3}-3Cs^{2}+Ds^{2}-3Ds$

$=90s^{2}-1110$

比较系数

A + B + C = 0

-15A - 12B - 3C + D = 90

73A + 37B - 3D = 0

-111A = -1110

现在，我们可以求解A，B，C 和 D

A = 10

B = -10

C = 0

D = 120

现在进行“拟合”

s² - 12s + 37 的根是 6 + j 和 6 - j

$A{\frac {1}{s}}+B{\frac {1}{s-3}}+C{\frac {s}{(s-6)^{2}+1^{2}}}+D{\frac {1}{(s-6)^{2}+1^{2}}}$

不需要对D 的分数进行拟合，因为它已经完整了；也不需要对C 的分数进行拟合，因为C 等于零。

$10{\frac {1}{s}}-10{\frac {1}{s-3}}+0{\frac {s}{(s-6)^{2}+1^{2}}}+120{\frac {1}{(s-6)^{2}+1^{2}}}$

${\frac {}{}}f(t)=10u(t)-10e^{3t}+120e^{6t}sin(t)$

终值定理

终值定理允许我们从 s 域方程确定时间域方程在时间趋于无穷大时的值。在控制工程中，终值定理最常用于确定系统的稳态值。函数极点的实部必须 < 0。

[终值定理 (拉普拉斯)]

$\lim _{t\to \infty }x(t)=\lim _{s\to 0}sX(s)$

从我们关于系统指标的章节中，您可能会认识到系统在时间趋于无穷大时的值为系统的稳态时间。稳态值与预期输出值之间的差值，我们称之为系统的稳态误差。使用终值定理，我们可以在复 s 域中找到系统的稳态值和稳态误差。

示例：终值定理

求以下多项式的终值

$T(s)={\frac {1+s}{1+2s+s^{2}}}$

我们可以应用终值定理

$\lim _{s\to \ 0}s{\frac {1+s}{1+2s+s^{2}}}$

我们得到的值为

$\lim _{s\to \ 0}s{\frac {1+s}{1+2s+s^{2}}}=0\cdot {\frac {1+0}{1+2\cdot 0+0^{2}}}=0\cdot 1=0$

初值定理

与终值定理类似，初值定理允许我们从 s 域方程确定系统的初始值（时间为零时的值）。初值定理最常用于确定系统的起始条件或“初始条件”。

[初值定理 (拉普拉斯)]

$x(0)=\lim _{s\to \infty }sX(s)$

常见变换

我们现在将向您展示我们已经学过的三个函数的变换：单位阶跃、单位斜坡和单位抛物线。单位阶跃函数的变换由下式给出

${\mathcal {L}}[u(t)]={\frac {1}{s}}$

由于单位斜坡是单位阶跃的积分，我们可以将上述结果乘以 *1/s* 来获得单位斜坡的变换

${\mathcal {L}}[r(t)]={\frac {1}{s^{2}}}$

同样，我们可以乘以 *1/s* 来获得单位抛物线的变换

${\mathcal {L}}[p(t)]={\frac {1}{s^{3}}}$

傅里叶变换

傅里叶变换非常类似于拉普拉斯变换。傅里叶变换假设任何有限时间域信号都可以分解为无限个正弦（正弦和余弦波）信号的总和。在这个假设下，傅里叶变换将时间域信号转换为其频域表示，作为径向频率 ω 的函数。傅里叶变换定义如下：

[傅里叶变换]

$F(j\omega )={\mathcal {F}}[f(t)]=\int _{0}^{\infty }f(t)e^{-j\omega t}dt$

可以使用以下 MATLAB 命令执行此操作

傅里叶

现在我们可以证明，当以下条件成立时，傅里叶变换等价于拉普拉斯变换

${\begin{matrix}s=j\omega \end{matrix}}$

由于拉普拉斯变换和傅里叶变换关系密切，对所有问题都使用这两种变换没有太大意义。因此，本书将重点关注拉普拉斯变换，几乎涵盖所有主题，除了直接处理频率值的那些问题。对于频率问题，使用傅里叶变换表示会让生活更容易。

与拉普拉斯变换一样，傅里叶变换也已在广泛的表格中列出。傅里叶变换的属性，以及常见变换的表格，可以在附录中找到。

逆傅里叶变换

可以使用以下 MATLAB 命令执行此操作

ifourier

逆傅里叶变换定义如下：

[逆傅里叶变换]

$f(t)={\mathcal {F}}^{-1}\left\{F(j\omega )\right\}={\frac {1}{2\pi }}\int _{-\infty }^{\infty }F(j\omega )e^{j\omega t}d\omega$

此变换与傅里叶变换几乎相同。

复平面

使用上述等价关系，我们可以证明，如果变量 *s* 是一个虚数，拉普拉斯变换始终等于傅里叶变换。但是，如果 *s* 是一个实数或复数变量，拉普拉斯变换就不同了。因此，我们通常定义 *s* 既有实部也有虚部，如下所示：

${\begin{matrix}s=\sigma +j\omega \end{matrix}}$

我们可以证明，如果 σ * = 0，则 *s = j*ω。

由于变量 *s* 可以分解为两个独立的值，因此在它自己的特殊“S 平面”上绘制变量 *s* 通常很有意义。S 平面在水平轴上绘制变量 σ，在垂直轴上绘制 *j*ω 的值。右侧显示了此轴排列。

欧拉公式

微积分中有一个重要的结果被称为欧拉公式或“欧拉关系”。这个重要的公式将 *e*、*j*、π、1 和 0 的重要值联系起来

${\begin{matrix}e^{j\pi }+1=0\end{matrix}}$

但是，这个结果是从以下等式推导出来的，将 ω 设置为 π

[欧拉公式]

${\begin{matrix}e^{j\omega }=\cos(\omega )+j\sin(\omega )\end{matrix}}$

此公式将在本书的某些章节中广泛使用，因此现在熟悉它很重要。

MATLAB

MATLAB 符号工具箱包含自动计算拉普拉斯变换和傅里叶变换的函数。函数 laplace 和函数 fourier 可分别用于计算输入函数的拉普拉斯变换和傅里叶变换。例如，代码

t = sym('t');
fx = 30*t^2 + 20*t;
laplace(fx)

生成输出

ans =

60/s^3+20/s^2

我们将在附录中详细讨论这些函数。

进一步阅读

• 数字信号处理/连续时间傅里叶变换
• 信号与系统/非周期信号
• 电路理论/拉普拉斯变换

← 系统建模

控制系统

传递函数 →