感觉系统/计算机模型/神经模拟
“动作电位”是神经系统中用于传播信号的典型电压变化。

使用下面描述的机制,传入的刺激(任何类型的)会导致神经细胞的电压电位发生变化。在达到一定阈值之前,这就是全部内容(图 4 中的“失败启动”。但当电压门控离子通道的阈值达到时,它会引起几乎立即完全打开 Na+ 离子通道的反馈反应(“去极化”):这会达到 Na+ 渗透性(在静息状态下约为 K+ 渗透性的 1%)比 K+ 大 20 倍的点。因此,电压从大约 -60mV 上升到大约 +50mV。在这一点上,内部反应开始关闭(并阻塞)Na+ 通道,并打开 K+ 通道以恢复平衡状态。在此“不应期”期间(约 1 毫秒),任何去极化都不能引起动作电位。只有当达到静息状态时,才能触发新的动作电位。
为了模拟动作电位,我们首先必须定义细胞膜的不同元素,以及如何以分析方式描述它们。
细胞膜由一层疏水、几乎不可渗透的蛋白质双层组成,即细胞膜。信号处理的真正力量不是来自细胞膜,而是来自嵌入该膜中的离子通道。离子通道是嵌入细胞膜中的蛋白质,它们可以选择性地为某些类型的离子打开。(这种选择性是通过组成离子通道的氨基酸的几何排列实现的。)除了上面提到的 Na+ 和 K+ 离子外,神经系统中通常发现的离子是阳离子 Ca2+、Mg2+ 和阴离子 Cl-。
离子通道可以处于三种状态之一
- 打开(例如,打开的 Na 通道可以让 Na+ 离子通过,但会阻塞所有其他类型的离子)。
- 关闭,但可以选择打开。
- 关闭,无条件。
典型默认情况 - 当没有任何事情发生时 - 的特点是 K+ 是打开的,而其他通道是关闭的。在这种情况下,两种力量决定了细胞电压
- K+ 的细胞内和细胞外浓度之间的(化学)浓度差,这种浓度差是由上述离子泵的持续活动产生的。
- 细胞内部和外部之间的(电)电压差。
平衡由能斯特方程定义
R ... 气体常数,T ... 温度,z ... 离子价态,F ... 法拉第常数,[X]o/i … 离子浓度(外/内)。在 25° C 时,RT/F 为 25 mV,导致静息电位为
在典型的 K+ 浓度下,神经元内外,这将产生 。如果同时考虑 K+、Na+ 和 Cl- 的离子通道,则平衡状态可以用戈德曼方程来描述
其中 Pi 表示离子“i”的渗透性,I 表示浓度。使用典型的离子浓度,细胞在其静息状态下具有大约 -60 mV 的负极性。
离子通道的激活
[edit | edit source]离子通道的一个重要特点是,它们的渗透性可以通过以下方式改变:
- 机械刺激(机械门控离子通道)
- 化学刺激(配体门控离子通道)
- 或外部电压(电压门控离子通道)
- 有时离子通道直接连接两个细胞,在这种情况下,它们被称为间隙连接通道。
重要
- 感觉系统本质上是基于离子通道的,这些离子通道被机械刺激(压力、声音、运动)、化学刺激(味觉、嗅觉)或电磁刺激(光)激活,并产生“神经信号”,即神经细胞中的电压变化。
- 动作电位利用电压门控离子通道,快速可靠地改变神经元的“状态”。
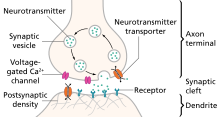
- 神经细胞之间的交流主要使用由神经递质激活的离子通道,即前一个神经元在突触处释放的化学物质。这为神经信号的处理提供了最大的灵活性。
模拟电压依赖性离子通道
[edit | edit source]欧姆定律将电阻器的电阻 R 与它通过的电流 I 和电阻器两端的电压降 V 联系起来
或者
其中 是电阻器的电导。如果你现在假设电导与通道处于开放构象的概率成正比,那么这个方程就变成了
其中 是通道的最大电导率,而 是通道处于开放构象的概率。
示例:K通道
电压门控钾离子通道 (Kv) 只能处于开放或关闭状态。设 α 为通道从关闭状态到开放状态的速率,β 为通道从开放状态到关闭状态的速率。
由于 n 是通道处于开放状态的概率,通道处于关闭状态的概率必须为 (1-n),因为所有通道都处于开放或关闭状态。因此,可以使用以下公式来描述通道构象的变化
请注意,α 和 β 是电压相关的!1952 年,霍奇金和赫胥黎使用一种名为“电压钳制”的技术来确定这些速率,并得出了类似于以下的公式
如果您只想对电压门控钾离子通道进行建模,则这些将是开始使用的方程式。(对于电压门控钠通道,方程式会更难,因为这些通道有三种可能的构象:开放、关闭和失活。)
霍奇金-赫胥黎方程式
[edit | edit source]上述提到的电压门控离子通道的反馈回路使得很难确定它们的精确行为。在第一近似中,动作电位的形状可以通过分析神经元单个轴突隔室的电路来解释,该电路包含以下组件:1)Na 通道,2)K 通道,3)Cl 通道,4)泄漏电流,5)膜电容,
霍奇金-赫胥黎模型中原始的最终方程式,其中氯离子和其它泄漏电流合并,如下所示

其中 , 和 是描述膜通透性的时间和电压相关函数。例如,对于 K 通道,n 遵循上面描述的方程式,这些方程式是通过电压钳制实验确定的。这些方程式可以高精度地描述动作电位的形状和传播!该模型可以使用开源工具轻松求解,例如 Python 动态系统工具箱 *PyDSTools*。一个简单的求解文件可在 [1] 下获得,输出如下所示。
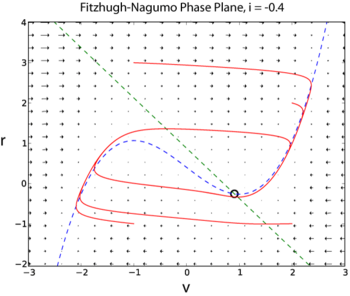
霍奇金-赫胥黎模型有四个动态变量:电压 ,K 通道打开的概率,,Na 通道在先前处于关闭状态时打开的概率,,以及 Na 通道在先前处于非活动状态时打开的概率,。神经元动作电位产生的简化模型是菲茨休-纳格莫 (FN) 模型。与霍奇金-赫胥黎模型不同,FN 模型只有两个动态变量,将变量 和 合并成单个变量 ,并将变量 和 合并成单个变量
以下两个例子来自 I 是注入神经元的外部电流。由于 FN 模型只有两个动态变量,因此可以使用相平面方法探索其完整动力学(此处提供 Python 中的示例解决方案[2])。
以下两个例子来自 [3] 。这本书对模拟简单神经系统进行了极好的介绍,并对潜在的信息处理提供了很好的理解。
首先,让我们看一下单个神经元的响应,其输入为 ,并且具有对其自身的反馈。输入的权重为 ,反馈的权重为 。神经元的响应 由以下给出
这表明即使是非常简单的模拟也能捕获真实神经元的信息处理特性。

""" Simulation of the effect of feedback on a single neuron """
import numpy as np
import matplotlib.pylab as plt
# System configuration
is_impulse = True # 'True' for impulse, 'False' for step
t_start = 11 # set a start time for the input
n_steps = 100
v = 1 # input weight
w = 0.95 # feedback weight
# Stimulus
x = np.zeros(n_steps)
if is_impulse:
x[t_start] = 1 # then set the input at only one time point
else:
x[t_start:] = 1 # step input
# Response
y = np.zeros(n_steps) # allocate output vector
for t in range(1, n_steps): # at every time step (skipping first)
y[t] = w*y[t-1] + v*x[t-1] # compute the output
# Plot the results
time = np.arange(n_steps)
fig, axs = plt.subplots(2, 1, sharex=True)
axs[0].plot(time, x)
axs[0].set_ylabel('Input')
axs[0].margins(x=0)
axs[1].plot(time, y)
axs[1].set_xlabel('Time Step')
axs[1].set_ylabel('Output')
plt.show()
模拟一个简单的神经系统
[edit | edit source]即使是非常简单的神经系统也能表现出令人惊讶的多功能行为。一个例子是 Wilson 对蝗虫飞行中央模式发生器的模型。在这里,系统由以下描述
W 是连接矩阵,描述了神经元的循环连接,并描述了系统的输入。


""" 'Recurrent' feedback in simple network:
linear version of Wilson's locust flight central pattern generator (CPG) """
import numpy as np
import matplotlib.pylab as plt
# System configuration
v = np.zeros(4) # input weight matrix (vector)
v[1] = 1
w1 = [ 0.9, 0.2, 0, 0] # feedback weights to unit one
w2 = [-0.95, 0.4, -0.5, 0] # ... to unit two
w3 = [ 0, -0.5, 0.4, -0.95] # ... to unit three
w4 = [ 0, 0, 0.2, 0.9 ] # ... to unit four
W = np.vstack( [w1, w2, w3, w4] )
n_steps = 100
# Initial kick, to start the system
x = np.zeros(n_steps) # zero input vector
t_kick = 11
x[t_kick] = 1
# Simulation
y = np.zeros( (4,n_steps) ) # zero output vector
for t in range(1,n_steps): # for each time step
y[:,t] = W @ y[:,t-1] + v * x[t-1] # compute output
# Show the result
time = np.arange(n_steps)
plt.plot(time, x, '-', label='Input')
plt.plot(time, y[1,:], ls='dashed', label = 'Left Motorneuron')
plt.plot(time, y[2,:], ls='dotted', label='Right Motorneuron')
# Format the plot
plt.xlabel('Time Step')
plt.ylabel('Input and Unit Responses')
plt.gca().margins(x=0)
plt.tight_layout()
plt.legend()
plt.show()
神经形态电路的开发和理论
[edit | edit source]介绍
[edit | edit source]神经形态工程使用超大规模集成 (VLSI) 系统来构建模拟和数字电路,模拟神经生物结构和行为。大多数现代电路主要利用数字电路组件,因为它们速度快、精度高且对噪声不敏感。与更具生物学意义的模拟电路不同,数字电路需要更高的电源,并且不能进行并行计算。生物神经元的行为,例如膜泄漏和阈值约束,是材料基底参数的函数,需要模拟系统来建模和微调,超出了数字 0/1。本文将简要概述此类神经形态电路及其模拟电路组件背后的理论。
神经形态工程的最新事件
[edit | edit source]在过去 10 年中,神经形态工程 领域经历了快速上升,并受到媒体和科学界的广泛关注。
在该主题引起欧盟委员会关注后,人类大脑项目于 2013 年启动,在十年内获得 6 亿欧元的资金。该项目的目的是从分子和神经元水平到神经回路模拟人脑。该项目计划于 2023 年 9 月结束,尽管主要目标尚未实现,但它提供了至少 200 个大脑区域的详细 3D 地图和超级计算机来模拟记忆和意识等功能,以及其他事物 [4]。另一个主要成果是 EBRAINS 虚拟平台,于 2019 年推出。它提供了一套工具和图像数据,全球科学家可以利用这些工具和数据进行模拟和数字实验。
同样在 2013 年,美国国立卫生研究院宣布为旨在重建大量神经元活动的 BRAIN 项目提供资金。该项目正在进行,截至 2023 年已拨款 6.8 亿美元。
近年来取得的其他重大成果列举如下
1. TrueNorth 芯片 (IBM,2014):总共 2.68 亿个可编程突触
2. Loihi 芯片 (英特尔,2017):基于异步神经尖峰网络 (SNN) 的自适应事件驱动并行计算。它在 2021 年被 Loihi2 取代。
3. 原型芯片 (IMEC,2017):首个基于 OxRAM 技术的自学习神经形态芯片
4. Akida AI 处理器开发套件 (Brainchip,2021):首个商用神经形态处理器
晶体管结构和物理
[edit | edit source]金属氧化物半导体场效应晶体管 (MOSFET) 是现代集成电路的常见组件。MOSFET 被归类为单极型器件,因为每个晶体管只利用一种载流子类型;负型 MOFET (nFET) 的载流子为电子,正型 MOSFET (pFET) 的载流子为空穴。
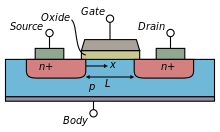
一般的 MOSFET 具有金属栅极 (G) 和两个称为源极 (S) 和漏极 (D) 的 pn 结二极管,如图 \ref{fig: transistor} 所示。有一个绝缘氧化物层将栅极与硅体 (B) 隔开。承载电荷的通道直接位于此氧化物层下方。电流是栅极尺寸的函数。
源极和漏极是对称的,只有施加的偏置不同。在 nFET 器件中,形成源极和漏极的阱为 n 型,位于 p 型衬底中。衬底通过体 p 型阱触点进行偏置。正电流在通道中从漏极流向源极,位于栅极下方。源极之所以被称为源极,是因为它是电子的来源。相反,在 pFET 器件中,p 型源极和漏极位于 n 型衬底中的体 n 阱中;电流从源极流向漏极。
当载流子由于浓度梯度而移动时,这称为扩散。如果载流子由于电场而被驱使,则称为漂移。按照惯例,nFET 漏极的偏置电压高于源极,而 pFET 的源极偏置电压高于漏极。
在 nFET 中,当在栅极上施加正电压时,正电荷会在金属触点上累积。这会从体硅中吸引电子到硅氧化物界面,在源极和漏极之间形成一个带负电的通道。栅极电压越大,通道越厚,内部电阻越小,电流呈对数增长。对于较小的栅极电压,通常低于阈值电压,,通道尚未完全导通,从漏极到源极的电流在对数刻度上呈线性增长。当 时,称为亚阈值区。超过此阈值电压,,通道在源极和漏极之间完全导通,电流处于超阈值区。

为了使电流从漏极流到源极,最初必须有一个电场来驱动载流子穿过通道。该电场强度是源极和漏极之间施加的电位差 () 的函数,因此控制着漏极-源极电流。对于较小的 值,电流会随着 呈线性增长,前提是 值恒定。随着 超过 ,电流会饱和。
pFET 的行为与 nFET 类似,只是载流子是空穴,触点偏置是相反的。
在数字应用中,晶体管要么在其饱和区(开启)工作,要么处于关闭状态。这种导通和关闭模式之间的巨大电位差是数字电路具有如此高功耗的原因。相反,模拟电路利用晶体管的线性区来产生具有较低功耗的连续信号。然而,由于栅极或源极-漏极电压的微小变化会导致电流发生较大变化,因此模拟系统容易受到噪声的影响。
神经形态工程领域利用模拟电路的噪声特性来复制随机神经元行为 [5] [6]。与时钟驱动的数字电路不同,模拟电路能够产生具有类似生物时间尺度 (约 ) 的时间动态的动作电位。通过延长泄漏偏置和可变电阻晶体管的时间常数,电位被减慢,放电速率被控制。已经创建了能够模拟具有不同时间动态的生物动作电位的模拟电路,从而允许硅电路模仿神经元基于尖峰的学习行为 [7]。而数字电路只能包含二进制突触权重 [0,1],模拟电路能够在连续的值范围内保持突触权重,这使得模拟电路对于神经形态电路特别有利。
基本静态电路
[edit | edit source]理解了晶体管的工作原理及其偏置方式后,就可以通过基本静态模拟电路来进行合理化。随后,这些基本静态电路将被组合起来创建神经形态电路。在以下电路示例中,源极、漏极和栅极电压是固定的,电流是输出。在实际应用中,偏置栅极电压固定为亚阈值(),漏极保持在饱和状态(),源极和体极接地(,)。所有非理想性都被忽略。

二极管连接的晶体管
[edit | edit source]二极管连接的nFET将栅极连接到漏极。由于浮动漏极控制栅极电压,漏极-栅极电压将自调节,因此器件将始终吸收输入电流,。超过几个微伏,晶体管将进入饱和状态。类似地,二极管连接的pFET将栅极连接到源极。虽然这个简单的器件似乎仅仅作为一个短路工作,但它通常用于模拟电路中以复制和调节电流。特别是在神经形态电路中,它们被用来减缓电流汇,将电路时间常数增加到生物学上可信的时间范围。
电流镜
[edit | edit source]电流镜利用了二极管连接的晶体管吸收电流的能力。当输入电流被强制通过二极管连接的晶体管,,浮动漏极和栅极被调节到允许输入电流通过的适当电压。由于两个晶体管共享一个公共栅极节点,也将吸收相同的电流。这迫使输出晶体管复制输入电流。只要
- .
可以通过调整这两个参数来控制电流镜增益。当使用不同尺寸的晶体管时,即倾斜镜,增益为
pFET电流镜只是一个翻转的nFET镜,其中二极管连接的pFET反映输入电流,并迫使另一个pFET源极输出电流。
电流镜通常用于复制电流而不消耗输入电流。这对于反馈回路尤其重要,例如用于加速动作电位的反馈回路,以及在突触处对输入电流求和。
源极跟随器
[edit | edit source]源极跟随器由一个输入晶体管 ,叠加在一个偏置晶体管 上方组成。固定的亚阈值 () 偏置电压控制栅极 ,迫使其以恒定电流 汇流。因此, 也被强制以相同的电流 () 汇流,无论输入电压 是什么。
源极跟随器之所以被称为源极跟随器,是因为输出 将跟随 ,并伴随一个由以下公式描述的微小偏移:
其中 kappa 是亚阈值斜率因子,通常小于 1。
这个简单的电路通常用作缓冲器。由于没有电流可以流过栅极,因此该电路不会从输入端汲取电流,这对于低功耗电路来说是一个重要的特性。源极跟随器还可以隔离电路,保护电路免受电源浪涌或静电的影响。pFET 源极跟随器与 nFET 源极跟随器唯一的区别在于偏置 pFET 的体端连接到 。
在神经形态电路中,源极跟随器等被用作简单的电流积分器,其行为类似于从多个突触前神经元收集电流的突触后神经元。
反相器
[edit | edit source]反相器由一个 pFET ,叠加在一个 nFET 上方组成,它们的栅极连接到输入 ,输出连接到公共源极节点 。当输入高电平时,pFET 关闭,但 nFET 打开,有效地放电输出节点 ,并反转信号。相反,当输入信号为低电平时,nFET 关闭,但 pFET 打开,为 节点充电。
这个简单的电路可以有效地用作快速开关。反相器也常被用作缓冲器,因为可以在不直接提供输入电流的情况下产生输出电流,因为不允许电流流过栅极。当两个反相器串联使用时,它们可以用作非反相放大器。这在 Mead 等人 1989 年的原始积分-触发硅神经元中被用来产生类似于生物动作电位的快速去极化尖峰 [8]。然而,当输入在高信号和低信号之间波动时,两个晶体管都处于超阈值饱和状态,消耗电流,这使得它成为一个非常耗电的电路。
电流传送器也常被称为缓冲电流镜像。电流传送器由两个晶体管组成,它们的栅极连接到对方的节点,其自调节方式使得输出电流与输入电流匹配,类似于电流镜像。
电流传送器通常用在需要大规模串联重复阵列的场合,用来代替电流镜像。这是因为电流镜像的电流通过栅极来控制,栅极的氧化层电容会导致输出延迟。虽然这种延迟对于单个输出电流镜像来说可以忽略不计,但是对于长的镜像阵列,累积的输出延迟会变得相当明显。这种延迟会严重阻碍大型并行过程,例如那些试图模拟生物神经网络计算策略的过程。
差分对是一个比较电路,由两个共用偏置的源极跟随器组成,该偏置强制较弱的输入电流被抑制。偏置晶体管将强制 保持恒定,将公共节点 连接到固定电压。两个输入晶体管都希望根据其输入电压 和 分别消耗电流。然而,由于公共节点必须保持固定,所以输入晶体管的漏极必须根据栅极电压升高。具有较低输入电压的晶体管将充当阻扼器,允许更少的电流通过其漏极。输掉竞争的晶体管会看到其源极电压升高,从而脱离饱和状态。
在神经元电路的设置中,差分对可以作为离子通道的激活阈值,低于该阈值,电压门控离子通道不会打开,从而阻止神经元产生尖峰 [9]。
胜者全拿 (WTA) 电路最初由 Lazzaro 等人设计 [10],它是一个连续时间模拟电路。它比较了一组单元的输出,只允许输出电流最大的单元开启,抑制所有其他竞争单元。

每个单元包含一个电流控制传送器,接收输入电流,并将电流输出到控制偏置晶体管的公共线上。具有最大输入电流的单元也将输出最大电流,从而提高公共节点的电压。这将迫使较弱的单元关闭。WTA 电路可以扩展到包含大量的竞争单元网络。软 WTA 还将输出电流镜像回输入,有效地增加了单元增益。这对于减少噪声和随机切换是必要的,特别是当单元阵列的动态范围较小时。
WTA 网络通常用作计算神经网络中竞争学习的一种形式,这些网络涉及分布式决策。特别是,WTA 网络已被用于执行更接近视觉选择任务期间皮层活动的下层识别和分类任务 [11]。
积分发射神经元的最通用示意图,也被称为轴突丘神经元,是最常用的尖峰神经元模型 [8]。大多数轴突丘电路的共同元素包括:一个节点,它记忆着膜电位 ,一个放大器,一个正反馈回路 ,以及一个将膜电位重置到静息状态的机制, .
输入电流 为 充电,储存在电容 C 中。该电容类似于脂质细胞膜,它阻止了自由离子扩散,从而在脂质膜两侧累积的电荷差产生膜电位。输入被放大以输出电压尖峰。膜电位的变化通过 对 进行正反馈,产生更快的尖峰。这与生物轴突丘的运作方式非常相似,轴突丘密集地排列着电压门控钠通道,它放大了累积的电位以产生动作电位。当产生电压尖峰时,复位偏压 开始耗尽 节点。这类似于钠钾通道,它主动地将钠离子和钾离子泵到浓度梯度,以维持静息膜电位。


原始轴突丘硅神经元已被改造成包含一个激活阈值,添加了一个差分对,将输入与一个设定的阈值偏压 [9] 进行比较。这种基于电导的硅神经元利用带泄漏晶体管的差分对积分器(DPI)来比较输入 和阈值 。泄漏偏压 、不应期偏压 、适应偏压 和正反馈增益,都可以独立地控制尖峰频率。研究重点在于实现尖峰频率适应,以设置不应期和调节阈值 [12]。适应允许神经元根据其输入调节其输出发射率。如果有恒定的高频输入,神经元会对输入变得不敏感,随着时间的推移,输出会逐渐减弱。基于电导的神经元电路的自适应组件通过钙通量建模,并通过自适应电容 存储过去活动的记忆。尖峰频率适应的出现使得可以在神经元层面上进行改变,以控制突触层面的自适应学习机制。这种神经元学习模型是根据生物学 [13] 建模的,将在 Silicon Synapses 中进一步讨论。
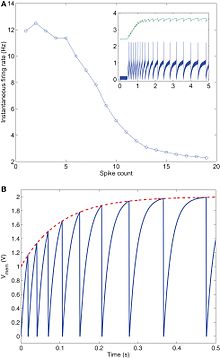
最基本的硅突触,最初由 Mead 等人于 1989 年使用 [8],它只是一个 pFET 源极跟随器,接收低信号脉冲输入并输出单向电流, [14]。

尖峰的幅度由权重偏置控制,,脉冲宽度与输入脉冲宽度直接相关,输入脉冲宽度由 $V_{\tau}$ 设置。Lazzaro 等人(1993 年)的突触电路中的电容器被添加以将尖峰时间常数增加到生物学上合理的数值。这减缓了脉冲过极化和去极化的速率,并且是电容的函数。

对于描绘竞争性兴奋和抑制行为的多个输入,对数域积分器使用 和 来调节输出电流幅度,,作为输入电流的函数,,根据
控制 为输出晶体管栅极充电的速率。 控制输出 被吸收的速率。这种竞争性是模仿神经递质的生物学行为所必需的,神经递质可以促进或抑制神经元的放电。
突触模型也使用对数域滤波器开发了具有阶次线性积分器,这些滤波器能够模拟兴奋性突触后电流 (EPSC) 的指数衰减 [15]。这是为了获得生物学上合理的尖峰轮廓和时间常数所必需的。增益也独立于突触时间常数控制,这对于尖峰速率和尖峰时间相关的学习机制是必需的。

上述突触只是简单地中继来自突触前来源的电流,在此过程中改变脉冲尖峰的形状。但是,它们不包含任何关于先前尖峰的记忆,也不能够根据时间动态来适应它们的行为。然而,这些能力对于神经形态电路像生物神经网络一样学习是必需的。

根据 Hebb 假设,学习和记忆等行为被假设发生在突触水平 [16]。它将学习过程归因于长期神经元适应,其中突触前和突触后贡献通过生化修饰得到增强或减弱。该理论通常总结为一句话:“一起发射的神经元,一起连接”。人工神经网络通过这些生化“连接”修饰来模拟学习,仅用一个参数来表示,即突触权重 。突触权重是一个参数状态变量,它量化了突触前神经元峰值如何影响突触后神经元输出。Hebb 突触权重可塑性的两种模型包括峰值率依赖可塑性 (SRDP) 和峰值时间依赖可塑性 (STDP)。自从该理论提出以来,生物神经元活动已被证明表现出与 Hebb 学习密切相关的行为。一个例子是导致钙流入诱导适应的突触 NMDA 和 AMPA 受体可塑性修饰 [17]。
生物神经元中信息的学习和长期记忆归因于 NMDA 通道诱导的适应。这些 NMDA 受体是电压依赖的,并控制细胞内钙离子流。动物研究表明,当细胞外钙减少时,神经元脱敏会减少 [17]。

由于钙浓度呈指数衰减,这种行为很容易使用亚阈值晶体管在硬件上实现。Rachmuth 等人 (2011) [18] 展示了一个模拟钙依赖性生物行为的电路模型。钙信号 通过 节点调节 AMPA 和 NMDA 通道活性,根据钙依赖性 STDP 和 SRDP 学习规则进行调节。这些学习规则的输出是突触权重 ,它与活性 AMPA 和 NMDA 通道的数量成正比。SRDP 模型用两个状态变量来描述权重, 控制更新规则, 控制学习率。
其中 是突触权重, 是更新规则, 是学习率,而 是一个常数,允许在没有输入的情况下,权重漂移出饱和状态。
NMDA 通道控制钙离子流入,。NMDA 受体电压依赖性由 建模,通道机制由一个大的电容器控制,以增加钙离子时间常数,。输出 通过电流镜像复制到 和 电路中,以执行下游学习功能。
电路将 与阈值偏置进行比较, 和 ),分别通过一系列差分对电路控制长时程增强或长时程抑制。差分对的输出决定更新规则。此 电路已被证明能够表现出海马体中观察到的各种 Hebbian 学习规则,以及小脑中使用的反 Hebbian 学习规则。
电路控制何时可以发生突触学习,方法是仅在 高于差分对设置的阈值时才允许更新,。学习率 (LR) 按照以下模型进行:
其中 是 的函数,控制学习率, 是 电路的电容, 是比较器的阈值电压。此函数表明 必须被偏置以维持较高的 以模拟 SRDT。一个漏电流,,被包含进来以在不活动期间将 排放到 。
NEURON 模拟环境
[edit | edit source]介绍
[edit | edit source]Neuron 是一个模拟环境,您可以使用它来模拟生物和人工神经元以及神经元网络中的离子传播和动作电位 [19]。用户可以通过定义和连接神经元细胞部分来指定模型几何形状,这些部分可以配备各种机制,例如离子通道、夹具和突触。为了与 NEURON 交互,用户可以使用图形用户界面 (GUI) 或其中一种编程语言 hoc(一种具有类似 C 语法的语言)或 Python 作为解释器。GUI 包含了最常用功能的广泛选择,右侧的图片显示了一个屏幕截图示例。另一方面,编程语言可以被利用来为模型添加更具体的机制并用于自动化目的。此外,可以使用编程语言 NMODL 创建自定义机制,它是 MODL 的扩展,MODL 是由 NBSR(国家生物医学模拟资源)开发的模型描述语言。然后可以编译这些新机制,并通过 GUI 或解释器添加到模型中。
Neuron 最初由杜克大学的 John W. Moore 与 Michael Hines 合作开发。它目前在许多研究所和大学中被用于教育和研究目的。有大量的信息可用,包括包含文档的官方网站、NEURON 论坛以及各种教程和指南。此外,2006 年出版了 NEURON 的权威参考书,名为“NEURON 手册” [20]。要阅读以下章节并使用 NEURON,建议您了解一些关于神经元生理学的背景知识。关于神经元的一些信息来源示例是 WikiBook 章节,或 Khan 学院 高级神经系统生理学 章节介绍中的视频。由于本文档不是教程,而只是对 NEURON 中的可能性和模型结构的概述,因此我们不会涵盖有关如何使用 NEURON 执行此处提及的操作的具体命令或细节。有关使用 NEURON 进行实现的更多实用信息,我建议您查看下面链接的教程和官方网页上的文档 [19]。
模型创建
[edit | edit source]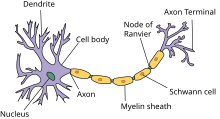
单细胞几何
[edit | edit source]首先我们将讨论创建一个由单个生物神经元组成的模型几何形状。右侧的图片显示了神经元的示意图。在以下列表中,展示了一个示例代码片段,其中使用 hoc 指定了一个具有一个胞体和两个树突的多室细胞。
load_file("nrngui.hoc")
// Create a soma object and an array containing 2 dendrite objects
ndend = 2
create soma, dend[ndend]
access soma
// Initialize the soma and the dendrites
soma {
nseg = 1
diam = 18.8
L = 18.8
Ra = 123.0
insert hh
}
dend[0] {
nseg = 5
diam = 3.18
L = 701.9
Ra = 123
insert pas
}
dend[1] {
nseg = 5
diam = 2.0
L = 549.1
Ra = 123
insert pas
}
// Connect the dendrites to the soma
connect dend[0](0), soma(0)
connect dend[1](0), soma(1)
// Create an electrode in the soma
objectvar stim
stim = new IClamp(0.5)
// Set stimulation parameters delay, duration and amplitude
stim.del = 100
stim.dur = 100
stim.amp = 0.1
// Set the simulation end time
tstop = 300
部分
[edit | edit source]NEURON 中的基本构建块称为“节段”。最初,一个节段只代表一个圆柱形管,具有长度和直径等单独属性。通过为节段配备相应的机制,例如离子通道或与其他细胞或人工刺激的突触连接,可以将其用于表示不同的神经元部分,例如胞体、树突或轴突。然后,可以通过以您想要的方式连接节段的末端来创建神经元细胞,例如以树状结构,只要没有循环即可。上面列表中指定的神经元在右侧的图中可视化。
为了更准确地模拟动作电位在节段中的传播,可以将节段细分为称为“段”的更小的部分。将节段分成多个段的模型称为“多室”模型。增加段的数量可以看作是增加空间离散化的粒度,这在例如膜特性沿节段不均匀时会导致更准确的结果。默认情况下,一个节段包含一个段。
节段的默认设置不包含任何离子通道,但用户可以添加它们 [21]。有两种类型的内置离子通道膜机制可用,即被动离子通道膜模型和 霍奇金-赫克斯利模型 膜模型,它代表了被动和电压门控离子通道的组合。如果这还不够,用户可以使用 NMODL 编程语言定义自己的膜机制。
除了在膜区域定义的膜机制外,还有称为“点过程”的局部机制可以添加到节段。一些例子是突触,如右侧的图所示,以及电压和电流钳位。同样,用户可以自由地使用 NMODL 编程语言实现自己的机制。点过程和膜机制之间的一个主要区别是,用户可以指定应该将点过程添加到节段上的位置,因为它是一种局部机制 [21]。
可以跟踪计算量的变化并绘制它们,例如创建特定段内电压随时间的变化的图形,如上面的 GUI 屏幕截图所示。也可以制作动画,例如显示轴突内电压分布随时间的变化。请注意,这些数量仅在每个段的中心和每个节段的边界处计算。
除了模拟单个细胞内的离子浓度外,还可以连接细胞并模拟神经元网络。为此,用户必须将突触(它们是点过程)连接到突触后神经元,然后创建“NetCon”对象,它们将充当突触前神经元和突触后神经元之间的连接。用户可以将不同类型的突触连接到神经元,例如AlphaSynapse,其中突触电导根据 alpha 函数衰减,以及ExpSyn,其中突触电导呈指数衰减。与其他机制一样,也可以使用 NMODL 创建自定义突触。对于 NetCon 对象,可以指定几个参数,例如阈值和延迟,它们决定突触前神经元引起突触后电位的必要条件。
除了我们到目前为止讨论过的生物神经元外,还有一种可以用 NEURON 模拟的神经元类型,称为“人工”神经元。NEURON 中生物神经元和人工神经元之间的区别在于,人工神经元没有空间范围,并且它的动力学高度简化。NEURON 中有几种积分器可用于模拟人工细胞的行为,它们在生物神经元动力学的简化程度上有所不同 [22]。为了减少人工尖峰神经元细胞和网络模型的计算时间,NEURON 的开发人员选择支持事件驱动的模拟。这大大减少了模拟尖峰触发的突触传递的计算负担。虽然对基于电导的神经元细胞进行建模需要连续系统模拟,但 NEURON 仍然可以通过完全支持混合模拟来利用事件驱动方法对包含生物和人工神经元的网络的益处。这样,任何组合的人工和基于电导的神经元细胞都可以被模拟,同时仍然可以实现由人工细胞的事件驱动模拟带来的减少的计算时间 [23]。用户还可以使用 NMODL 添加其他人工神经元类。

自 1984 年以来,NEURON 为创建和执行模拟提供了 hoc 解释器。hoc 语言已被扩展和维护,直到现在仍与 NEURON 一起使用,但由于这种维护需要大量时间,并且它已被证明是一种仅限于 NEURON 用户的孤儿语言,NEURON 的开发人员希望采用更现代的编程语言作为 NEURON 的解释器。由于 Python 在科学计算领域得到广泛应用,许多用户创建了包含可重用代码的包,因此现在它作为解释器比 hoc 更具吸引力 [24]。有三种方法可以使用 Python 与 NEURON 一起使用。第一种方法是使用终端运行 NEURON,接受交互式 Python 命令。第二种方法是使用解释器 hoc 运行 NEURON,并通过 hoc 中的特殊命令访问 Python 命令。第三种方法是将 NEURON 作为 Python 的扩展模块使用,这样就可以将 NEURON 模块导入到 Python 或 IPython 脚本中。
要使用第一种和第二种模式,即使用嵌入式 Python 与 NEURON 一起使用,完成简单的安装就足够了。但是,要使用第三种模式,即将 NEURON 作为 Python 的扩展模块使用,则需要从源代码构建 NEURON 并安装 Python 的 NEURON 共享库,这在 此安装指南 中有解释。
由于 NEURON 最初是使用 hoc 作为解释器开发的,因此用户仍然需要在 Python 中显式调用 hoc 函数和类。所有存在于 hoc 中的函数和类都可以通过模块“neuron”在 Python 中访问,无论是在使用嵌入在 NEURON 中的 Python 时,还是在使用 NEURON 作为扩展模块时。NEURON 在 hoc 和 Python 中的命令之间只有细微的差异,因此用户从一种语言切换到另一种语言时不应该遇到很多问题 [24]。使用 NEURON 与 Python 而不是 hoc 有几个优势。主要优势之一是 Python 提供了更多功能,因为它是一种完整的面向对象语言,并且有大量适用于科学和工程的分析工具。此外,从 NMODL 脚本加载用户定义的机制变得更容易,这使得 NEURON 更具吸引力,尤其是在模拟非常特定的机制时 [24]。有关 NEURON 与 Python 结合使用的更多详细信息,请点击 这里。
教程
[edit | edit source]
在线有多个教程可供您使用,以帮助您开始使用 NEURON,其中两个列在下面。
在 第一个教程 中,您将从学习如何创建一个单隔室细胞开始,并最终创建如图所示的神经元网络,其中包含自定义细胞机制。同时,您将通过 NEURON 的模板、自动化、计算时间优化和提取结果数据的特性进行指导。教程使用 hoc 命令,但程序在 Python 中几乎相同。
在 第二个教程 中,它展示了如何创建一个具有被动细胞膜和突触刺激的细胞,以及如何使用 Python 模块 matplotlib 可视化结果。
进一步阅读
[edit | edit source]除了本 NEURON 简介中提到的内容之外,还有许多其他选项可供使用,这些选项正在不断得到开发人员的扩展和改进。在“NEURON 书籍” [20] 中可以找到对 NEURON 的广泛解释,它是官方参考书籍。此外,官方网站 包含大量信息和指向其他资源的链接。
参考文献
[edit | edit source]另外两个来源是 Chicca 等人的“一种自适应硅突触” [25] 和 Liu 等人的“模拟 VLSI:电路与原理” [26]。
- ↑ T. Haslwanter (2012). "Hodgkin-Huxley Simulations [Python]". private communications.
- ↑ T. Haslwanter (2012). "Fitzhugh-Nagumo Model [Python]". private communications.
- ↑ T. Anastasio (2010). "Tutorial on Neural systems Modeling".
- ↑ 欧洲花费了 6 亿欧元来在计算机中重现人脑。结果如何?
- ↑ E Aydiner, AM Vural, B Ozcelik, K Kiymac, U Tan (2003), 一种简单的混沌神经元模型:神经网络的随机行为
{{citation}}: CS1 maint: multiple names: authors list (link) - ↑ WM Siebert (1965), 主要听觉神经元的随机行为的一些意义
- ↑ G Indiveri, F Stefanini, E Chicca (2010), 使用广义积分和发射硅神经元进行基于尖峰的学习
{{citation}}: CS1 maint: multiple names: authors list (link) - ↑ a b c CA Mead (1989), 模拟 VLSI 和神经系统
- ↑ a b RJ Douglas, MA Mahowald (2003), 硅神经元
- ↑ J Lazzaro, S Ryckebusch, MA Mahowald, CA Mead (1989), 胜者为王:网络的 复杂度
{{citation}}: CS1 maint: multiple names: authors list (link) - ↑ M Riesenhuber,T Poggio(1999),皮层中物体识别的层次模型
- ↑ E Chicca,G Indiveri,R Douglas(2004),基于事件的集成-发射神经元 VLSI 网络
{{citation}}:CS1 maint:作者列表有多个姓名 (link) - ↑ G Indiveri,E Chicca,R Douglas(2004),具有基于尖峰学习突触的 VLSI 可重构集成-发射神经元网络
{{citation}}:CS1 maint:作者列表有多个姓名 (link) - ↑ J Lazzaro,J Wawrzynek(1993),低功耗硅神经元、轴突和突触
- ↑ S Mitra,G Indiveri,RE Cummings(2010),用于具有全局参数控制的硅突触的对数域积分器的合成
{{citation}}:CS1 maint:作者列表有多个姓名 (link) - ↑ DO Hebb(1949),行为的组织
- ↑ a b PA Koplas,RL Rosenberg,GS Oxford(1997),钙在去敏化大鼠背根神经节神经元辣椒素反应中的作用
{{citation}}:CS1 maint:作者列表有多个姓名 (link) - ↑ G Rachmuth,HZ Shouval,MF Bear,CS Poon(2011),基于生物物理的尖峰速率-时间依赖性可塑性神经形态模型
{{citation}}:CS1 maint:作者列表有多个姓名 (link) - ↑ a b Neuron,用于神经元和神经元网络的基于经验的模拟
- ↑ a b Nicholas T. Carnevale,Michael L. Hines(2009),NEURON 手册
- ↑ a b NEURON 教程 1
- ↑ M.L. Hines 和 N.T. Carnevale(2002),NEURON 模拟环境
- ↑ Romain Brette,Michelle Rudolph,Ted Carnevale,Michael Hines,David Beeman,James M. Bower,Markus Diesmann,Abigail Morrison,Philip H. Goodman,Frederick C. Harris Jr.,Milind Zirpe,Thomas Natschläger,Dejan Pecevski,Bard Ermentrout,Mikael Djurfeldt,Anders Lansner,Olivier Rochel,Thierry Vieville,Eilif Muller,Andrew P. Davison,Sami El Boustani,Alain Destexhe(2002),尖峰神经元网络的模拟:工具和策略的综述
{{citation}}:CS1 maint:作者列表有多个姓名 (link) - ↑ a b c Hines ML,Davison AP,Muller E. NEURON 和 Python。神经信息学前沿。2009;3:1。doi:10.3389/neuro.11.001.2009。(2009),NEURON 和 Python
{{citation}}:CS1 maint:作者列表有多个姓名 (link) - ↑ E Chicca,G Indiveri,R Douglas(2003),自适应硅突触
{{citation}}:CS1 maint:作者列表有多个姓名 (link) - ↑ SC Liu,J Kramer,T Delbrück,G Indiveri,R Douglas(2002),模拟 VLSI:电路和原理
{{citation}}:CS1 maint:作者列表有多个姓名 (link)

![{\displaystyle {{E}_{X}}={\frac {RT}{zF}}\ln {\frac {{[X]}_{o}}{{[X]}_{i}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e2d5c294b8784f463d80357bd660f5e515b23a8)
![{\displaystyle {{E}_{X}}={\frac {25mV}{z}}\log {\frac {{[X]}_{o}}{{[X]}_{i}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49ea1afb0f8c662cb48929a3da01c5acdd4d6f88)

![{\displaystyle {{V}_{m}}={\frac {RT}{F}}\ln {\frac {{{P}_{K}}{{[{{K}^{+}}]}_{o}}+{{P}_{Na}}{{[N{{a}^{+}}]}_{o}}+{{P}_{Cl}}{{[Cl-]}_{i}}}{{{P}_{K}}{{[{{K}^{+}}]}_{i}}+{{P}_{Na}}{{[N{{a}^{+}}]}_{i}}+{{P}_{Cl}}{{[Cl-]}_{o}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a99888fc4b3f0858a0551a76f813fa566c3c7e2)



















































































![{\displaystyle dw=\eta ([Ca_{2+}])\cdot (\Omega ([Ca_{2+}])-\lambda w),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c904f8985f83bcc0f7cfbb240a97f5b6db16b3e)
![{\displaystyle \Omega ([Ca_{2+}])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8365820f3ba6b3eb8631a0bb5ce819be1ec17d1)
![{\displaystyle \eta ([Ca_{2+}])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9d4224f92cfee5905b380eb00eff81b77a2fe12)







![{\displaystyle \tau _{LR}\sim {\frac {\theta _{\eta }\cdot C_{\eta }}{I_{\eta }\cdot [Ca_{2+}]}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20bac65985bece7edd0e340742a5312609aa49b9)
![{\displaystyle [Ca_{2+}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4caea324562bc2c0bd11d4c73ed9eea47405b55)






