感觉系统/计算机模型/听觉系统仿真

感觉系统

视觉
听觉
平衡
触觉
嗅觉
味觉

技术方面

植入物
模型

动物中的

鸟类
鱼类
海洋动物
节肢动物
其他动物

听觉系统的计算机仿真

处理声音

音频信号可以存储在多种格式中。它们可以是未压缩的或压缩的，编码可以是开放的或专有的。在 Windows 系统上，最常见的格式是 WAV 格式 (w: WAV)。它包含一个标题，其中包含有关通道数量、采样率、每样本位数等的的信息。该标题后跟数据本身。通常的比特流编码是线性脉冲编码调制 (LPCM，(w: Pulse-code_modulation) 格式。

许多编程语言提供用于读取和写入 WAV 文件的命令。当使用其他格式的数据时，你有两种选择

• 你可以将它们转换为 WAV 格式，然后继续。一个非常全面的免费跨平台解决方案来录制、转换和流式传输音频和视频是 ffmpeg (http://www.ffmpeg.org/).
• 或者，你可以获取用于读取/写入所需格式的特殊程序模块。

傅立叶变换回顾 (w:Fourier_transform)

要变换连续函数，可以使用傅立叶积分

$F(k)=\int _{-\infty }^{\infty }{f(t)}\cdot e^{-2\pi ikt}dt$

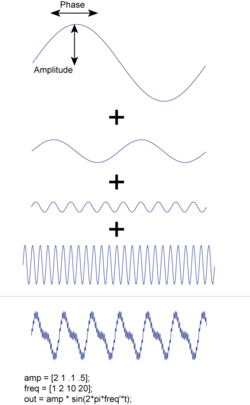
其中k代表频率。请注意，F(k)是复数值：它的绝对值给出函数的幅度，它的相位定义了余弦和正弦分量之间的相移。

逆变换由下式给出

$f(t)=\int _{-\infty }^{\infty }F(k)\cdot e^{2\pi ikt}dk$

傅立叶变换：正弦波的总和可以构成任何重复波形。

如果数据以恒定的采样频率进行采样，并且有N个数据点，则

$f(\tau )={\frac {1}{N}}*\sum _{n=0}^{N-1}F_{n}e^{2\pi in\tau /N}$

系数 Fn 可以通过以下方式获得

$F_{n}=\sum _{\tau =0}^{N-1}f(\tau )\cdot e^{-2\pi in\tau /N}$

由于数据点和波形的数量都是离散的、有限的，因此这种变换被称为 *离散傅里叶变换（DFT）*。 *快速傅里叶变换（FFT）* 只是 DFT 的一种特殊情况，其中点数为 2 的幂：$N=2^{n}$ 。

请注意，每个 $F_{n}$ 是一个复数：它的模定义了信号中对应频率成分的振幅；$F_{n}$ 的相位定义了相应的相位（见图示）。如果时域信号 "f(t)" 是实值的，就像大多数测量数据一样，这会对相应的频率成分施加约束：在这种情况下，我们有

$F_{n}=F_{N-n}^{*}$

一个常见的混淆来源是这个问题：“哪个频率对应于 $F_{n}$？”如果有 *N* 个数据点，采样周期为 $''T_{s}''$，$n^{th}$ 频率由下式给出

$f_{n}={\frac {n}{N\cdot T_{s}}},1\leq n\leq N(in\;Hz)$

换句话说，最低频率是 ${\frac {1}{N\cdot T_{s}}}$ [以 Hz 为单位]，而最高独立频率是 ${\frac {1}{2T_{s}}}$，这是由于奈奎斯特-香农定理。请注意，在 MATLAB 中，第一个返回值对应于函数的偏移量，第二个返回值对应于 n=1！

生物信号的频谱分析

平稳信号的功率谱

大多数 FFT 函数和算法返回复傅里叶系数 $F_{n}$。如果我们只对对应频率的贡献的大小感兴趣，我们可以通过以下方式获取此信息

$P_{n}={\frac {1}{N}}\cdot F_{n}\cdot F_{n}^{*}={\frac {1}{N}}\cdot |F_{n}|^{2}$

这就是我们信号的 *功率谱*，它告诉我们不同频率的贡献有多大。

非平稳信号的功率谱

通常人们必须处理随着时间变化其特征的信号。在这种情况下，人们想知道功率谱如何随时间变化。最简单的方法是每次只取一段短数据，并计算相应的功率谱。这种方法被称为 *短时傅里叶变换（STFT）*。但是，在这种情况下，边缘效应会显着扭曲信号，因为我们假设我们的信号是周期性的。

为了消除边缘伪影，可以对信号进行滤波或“加窗”（w: Window_function）。上图显示了这种窗口的一个示例。虽然有些窗口提供更好的频率分辨率（例如矩形窗口），但其他窗口表现出更少的伪影，例如频谱泄漏（例如汉宁窗口）。对于信号的选定部分，通过将信号与窗口相乘获得加窗后得到的数据（左图）

上面的右图显示了一个示例，说明如何切断信号并对其应用窗口会影响频谱功率分布。（相应的 Python 代码可以在 中找到）请注意，减小样本窗口的宽度会增加相应功率谱的宽度！

一个时间窗口的刺激强度

为了获得选定时间窗的功率谱，第一步是通过时间信号的快速傅里叶变换 (FFT) 计算功率谱。结果是频率域的声音强度及其对应的频率。第二步是将这些强度集中在几个不同的频率上（“分箱”）。结果是一个由几个不同频率组成的声音信号 - 模拟耳蜗中电极的位置。转换回时域将给出该时间窗的模拟声音信号。

以下 Python 函数对给定信号进行声音处理。

import numpy as np

def pSpect(data, rate):
    '''Calculation of power spectrum and corresponding frequencies, using a Hamming window'''
    nData = len(data)
    window = np.hamming(nData)
    fftData = np.fft.fft(data*window)
    PowerSpect = fftData * fftData.conj() / nData
    freq = np.arange(nData) * float(rate) / nData
    return (np.real(PowerSpect), freq)

def calc_stimstrength(sound, rate=1000, sample_freqs=[100, 200, 400]): 
    '''Calculate the stimulation strength for a given sound'''

    # Calculate the powerspectrum
    Pxx, freq = pSpect(sound, rate)

    # Generate matrix to sum over the requested bins
    num_electrodes = len(sample_freqs)
    sample_freqs = np.hstack((0, sample_freqs))
    average_freqs = np.zeros([len(freq), num_electrodes])
    for jj in range(num_electrodes):
        average_freqs[((freq>sample_freqs[jj]) * (freq<sample_freqs[jj+1])),jj] = 1

    # Calculate the stimulation strength (the square root has to be taken, to get the amplitude)
    StimStrength = np.sqrt(Pxx).dot(average_freqs)

    return StimStrength

耳廓和外耳的声音传导

外耳分为两部分：头部侧面的可见部分（耳廓）和通向鼓膜的外部耳道（外耳道），如下图所示。外耳以这种结构有助于人类声音定位能力的“频谱线索”，让人们不仅能够检测和识别声音，还能定位声源。

人耳的解剖结构

耳廓功能

耳廓的锥形使其能够收集声波并将它们引导到外耳道。除此之外，它的各种折叠使耳廓成为一个共振腔，可以放大某些频率。此外，由耳廓引起的声波反射产生的干涉效应是方向依赖的，并将衰减其他频率。因此，耳廓可以模拟为应用于入射声音的滤波函数，从而调节其幅度和相位谱。

耳廓对来自两个不同方向的声音的频率响应

耳廓腔的共振可以用 6 种正常模式很好地近似 。在这些正常模式中，第一种模式主要取决于耳甲深度（即最靠近耳道的耳廓碗状部分的深度），是最主要的模式。

由耳廓反射引起的某些频率的抵消称为“耳廓缺口”。 如右图所示 ，耳廓传来的声音经过两条路径，一条直接路径，另一条更长的反射路径。不同的路径具有不同的长度，从而产生相位差。当入射声音信号的频率达到一定标准时，即路径差为声波波长的一半，通过直接路径和反射路径的声音的干涉将是破坏性的。这种现象被称为“耳廓缺口”。通常缺口频率可能发生在 6k Hz 到 16k Hz 之间，具体取决于耳廓形状。还可以看出，耳廓的频率响应是方向依赖的。这使得耳廓有助于声音定位的空间线索。

耳道功能

外耳道大约 25 毫米长，8 毫米直径，从耳道入口到鼓膜呈弯曲路径。外耳道可以建模为一端封闭的圆柱体，导致共振频率约为 3k Hz。这样，外耳道就可以放大对人类语言重要的频率范围内的声音。

外耳模拟

基于外耳的主要功能，如果我们知道滤波器的特性，就可以很容易地用滤波器或滤波器组来模拟耳廓和外耳道的声波传导。

许多研究人员正在研究人类听觉系统的模拟，包括外耳的模拟。在下一章中，首先介绍了 _耳廓相关传递函数_ 模型，然后分别介绍了芬兰和英国研究小组开发的两个 MATLAB 工具箱。

Spagnol 的耳廓相关传递函数模型

这部分完全来自 S.Spagnol、M.Geronazzo 和 F.Avanzini 发表的论文。 为了模拟耳廓的功能，Spagnol 开发了一个耳廓相关传递函数 (PRTF) 的重建模型，该模型是一种频率响应，描述了耳廓如何传导声音。该模型由两个不同的滤波器模块组成，分别用于解释耳廓的共振功能和反射功能，如下图所示。

PRTF 重建的通用模型

在耳廓的感兴趣频率范围内，有两个主要的共振 ，可以用两个固定带宽的二阶峰值滤波器表示 $f_{b}=5kHz$

$H_{res}(z)={\frac {V_{0}(1-h)(1-z^{-2})}{1+2dhz^{-1}+(2h-1)z^{-2}}}$

其中

$h={\frac {1}{1+\tan(\pi {\frac {f_{B}}{f_{s}}})}}$

$d=-\cos(2\pi {\frac {f_{C}}{f_{s}}})$

$V_{0}=10^{\frac {G}{20}}$

和 $f_{s}$ 是采样频率，$f_{C}$ 是中心频率，$G$ 是陷波深度。

对于反射部分，设计了三个形式为 的二阶陷波滤波器，其参数包括中心频率 $f_{C}$，陷波深度 $G$ 和带宽 $f_{B}$。

$H_{refl}(z)={\frac {1+(1+k){\frac {H_{0}}{2}}+d(1-k)z^{-1}+(-k-(1+k){\frac {H_{0}}{2}})z^{-2}}{1+d(1-k)z^{-1}-kz^{-2}}}$

其中 $d$ 与之前为共振函数定义的相同，并且

$V_{0}=10^{\frac {-G}{20}}$

$H_{0}=V_{0}-1$

$k={\frac {\tan(\pi {\frac {f_{B}}{f_{s}}})-V_{0}}{\tan(\pi {\frac {f_{B}}{f_{s}}})+V_{0}}}$

每个滤波器对应一个不同的谱陷波。

通过将三个串联放置的陷波滤波器级联在两个并联的峰值滤波器之后，设计了一个八阶滤波器来模拟 PRTF。
通过比较合成 PRTF 和原始 PRTF，如下图所示，Spagnol 得出结论：PRTF 的合成模型总体上是有效的。由于截止频率的限制，该模型可能缺少陷波。由于可能存在未建模的干扰共振，也可能会引入近似误差。

原始 vs 合成 PRTF 图

HUTear MATLAB 工具箱

HUTear 通用听觉模型框图

HUTear 是由 声学与音频信号处理实验室 在 赫尔辛基理工大学 开发的用于听觉建模的 MATLAB 工具箱。这个开源工具箱可以从 这里 下载。工具箱的结构如右图所示。

该模型中包含一个用于“外耳和中耳 (OME)”仿真的模块。这个 OME 模型是基于 Glassberg 和 Moore 开发的。OME 滤波器通常是一个线性滤波器。听觉滤波器是在考虑“60 dB 等响度曲线 (ELC) ”、“最小可听场 (MAF)”、“耳道最小可听声压 (MAP)”校正的情况下生成的。该模型考虑了外耳仿真。通过使用“OEMtool”指定不同的参数，可以比较 MAP IIR 近似值和 MAP 数据，如下图所示。

HUTear 工具箱中的 OEMtool 用户界面

听觉外周模型 (MAP)

MAP 由英国埃塞克斯大学 埃塞克斯大学 听觉研究实验室 研究人员 开发 。MAP 是一个模拟人类听觉生理基础的计算机模型，它是一个开源代码包，用于测试和开发模型，可以从 这里 下载。其模型结构如下图所示。

MAP 模型结构

MAP 模型中包含“外中耳 (OME)”子模型，允许用户测试和创建 OME 模型。在这个 OME 模型中，外耳的功能被建模为一个共振函数。共振由两个并联的带通滤波器组成，分别代表耳廓共振和外耳道共振。这两个滤波器由通带频率范围、增益和阶数指定。通过将共振滤波器的输出添加到原始声压波中，可以得到外耳模型的输出。

为了测试 OME 模型，运行名为“testOME.m”的函数。将显示一个绘制外耳共振和镫骨峰值位移的图形。（如下图所示）

OME 模型中的外耳共振和镫骨峰值位移

总结

外耳，包括耳廓和外耳道，可以模拟为一个线性滤波器或滤波器组。这反映了它对传入声音的共振和反射效应。值得注意的是，由于耳廓形状因人而异，模型参数（如共振频率）取决于受试者。

上述模型中没有包含的一个方面是头部相关传递函数 (HRTF)。HRTF 描述了耳朵如何从空间中的一个点声源接收声音。这里没有介绍它，因为它超出了外耳（耳廓和外耳道）的影响范围，因为它还会受到头部和躯干的影响。对于感兴趣的读者，有很多关于 HRTF 的文献和出版物。（wiki，教程 1，2，关于空间音频研究（包括 HRTF）的阅读清单）

内耳仿真

基底膜的形状和组织意味着不同的频率在膜的不同位置产生特别强的共振。这导致膜上对频率范围敏感性的音调拓扑组织，可以将其建模为一组重叠的带通滤波器，称为“听觉滤波器”。 听觉滤波器与基底膜上的点相关联，并决定耳蜗的频率选择性，因此决定了听者对不同声音的辨别能力。 它们是非线性的，取决于声级，并且带宽从耳蜗的基底到顶点减小，因为基底膜上的调谐从高频到低频变化。 听觉滤波器的带宽被称为临界带宽，正如 Fletcher (1940) 首次提出的那样。如果一个信号和一个掩蔽物同时出现，那么只有落在临界带宽内的掩蔽物频率才有助于掩蔽信号。临界带宽越大，信噪比 (SNR) 越低，信号越容易被掩蔽。

ERB 与中心频率的关系。 该图显示了根据 Glasberg 和 Moore 的公式得到的 ERB 与中心频率的关系。

另一个与听觉滤波器相关的概念是“等效矩形带宽”(ERB)。ERB 显示了听觉滤波器、频率和临界带宽之间的关系。ERB 通过与之对应的听觉滤波器传递相同量的能量，并显示它如何随输入频率变化。 在低声级下，ERB 可以根据 Glasberg 和 Moore 的公式用以下方程近似。

$ERB=24.7*(4.37F+1)\,$

其中 ERB 以 Hz 为单位，F 以 kHz 为单位。

据认为，每个 ERB 等效于基底膜上大约 0.9 毫米。

伽马音滤波器

伽马音脉冲响应示例。

用于模拟听觉滤波器的一种滤波器类型是“伽马音滤波器”。它为描述给定声音输入下基底膜一个位置的运动提供了简单的线性滤波器，因此易于实现。线性滤波器常用于模拟听觉系统的不同方面。通常，它们是 IIR 滤波器（无限冲激响应），包含前馈和反馈，定义如下

$\sum \limits _{j=0}^{m}{{a_{j+1}}y(k-j)}=\sum \limits _{i=0}^{n}{{b_{i+1}}x(k-i)}$

其中 a1=1。换句话说，系数 ai 和 bj 唯一地决定了这种类型的滤波器。通过重新排列方程，可以更清楚地了解这些滤波器的反馈特性

$y(k)={b_{1}}x(k)+{b_{2}}x(k-1)+...+{b_{n+1}}x(k-n)-\left({{a_{2}}y(k-1)+...+{a_{m+1}}y(k-m)}\right)$

（相比之下，FIR 滤波器或有限冲激响应滤波器只涉及前馈：对于它们 $a_{i}=0$ 对于 i>1。）

“无限冲激响应”滤波器的通用描述。

线性滤波器无法解释听觉系统的非线性方面。然而，它们仍然被用于各种听觉系统模型。伽马音脉冲响应由以下公式给出：

$g(t)=at^{n-1}e^{-2\pi bt}\cos(2\pi ft+\phi ),\,$

其中 $f$ 是频率，$\phi$ 是载波的相位，$a$ 是振幅，$n$ 是滤波器的阶数，$b$ 是滤波器的带宽，$t$ 是时间。

这是一个正弦波，其幅度包络是一个缩放的伽马分布函数。

伽马音模型听觉滤波的变体和改进包括伽马啁啾滤波器、全极点和一零伽马音滤波器、双边伽马音滤波器和滤波器级联模型，以及这些模型的各种依赖于电平的和动态非线性版本。

对于计算机模拟，伽马音模型的有效实现可用于 Matlab 和 Python 。

在使用伽马音滤波器时，我们可以巧妙地利用帕塞瓦尔定理来确定给定频带的能量

$\int _{-\infty }^{\infty }{{{\left|{f(t)}\right|}^{2}}dt=}\int _{-\infty }^{\infty }{{{\left|{F(\omega )}\right|}^{2}}d\omega }$

听觉编码和耳蜗的滤波特性

在本页中，我们将回顾感知音频编码的主要机制。解释了背后的心理声学原理，并指出了与耳蜗的滤波特性和更高皮层处理阶段的关系。

感知音频编码

Mp3（MPEG-1 Layer 3，MPEG-2 和 MPEG-4 高级音频编码 (AAC) 的前身）可能是利用音频信号的感知编码的最著名的音频格式。 AAC 是一个更有效的扩展，通常可以获得更好的音质，允许更广泛的带宽，但依赖于与 Mp3 相同的编码原理。这两种格式都由 ISO 和 IEC 标准化，但只有解码器完全指定，而编码器实现是开放的。这导致了各种可用的编码器，其再现质量、可实现的比特率、性能和编码效率有所不同 。

与经典信号压缩算法（旨在用最少位数表示信息，同时保持信号再现质量）不同，感知音频编码考虑了来自人类听觉系统的知识，并通过去除对大多数听众来说感知上无关的信息来降低比特率。这种 有损压缩 是通过探索人类听觉系统的特性和统计冗余来实现的。Mp3 通常使用的编码比特率为 128 kbit/s，高效编码器在压缩 CD 质量音频（16 位 PCM，44.1 kHz，≈ 1411 kBit/s）时通常可以实现大约 10 倍的数据缩减。换句话说，大约 90% 存储在 CD 上的数据无法被人耳感知。CD 质量是用户在听音乐时通常期望的（关于 CD 质量是否足以再现模拟原始音频存在着长期争论。在众多不同的专家观点中，这两个参考文献 可能对进一步阅读有所帮助）。对更有效的音频编码的需求来自网络、多媒体系统和存储应用，Mp3 最初是为了更有效地传输视听内容而创建的。

约翰斯顿研究了感知音频编码的理论极限，从而引出了感知熵的概念。根据测量结果，感知熵估计为每样本约 2 比特，适用于 CD 音质音频。最先进的编码器证实了这种效率，可实现透明的（接近）CD 音质音频编码。感知编码算法的质量通常通过听力测试来评估，最近也结合了用于客观测量感知音频质量的标准化算法，称为感知音频质量评估 (PEAQ)。

感知音频编码器的基本架构

感知音频编码器的基本架构

大多数感知音频编码器都可以用图中所示的基本架构来描述。分析滤波器组近似于人类听觉系统的时域和频域分析特性。输入被分割成帧，然后转换为一组可以量化和编码的参数。量化和编码阶段利用统计冗余，并依赖于感知模型提供的阈值进行比特分配和量化噪声整形。感知模型描述了编码的频率函数掩蔽阈值。最后，编码阶段使用标准的无损编码技术，例如霍夫曼编码。有关技术算法解释和示例实现，我建议您参考J.O. Smith 的在线书籍。

用于感知音频编码的听觉心理声学原理

感知音频编码的基本思想是，对量化噪声进行整形，使其被音频信号本身掩蔽，从而不被听众感知。这是通过利用听觉心理声学原理实现的，包括绝对听阈、临界频带频率分析和听觉掩蔽。由于回放电平通常在编码阶段未知，因此在编码过程中，通常使用保守估计来评估绝对听阈，以进行信号归一化。听觉掩蔽描述了一种现象，即一种声音的感知会受到另一种声音存在的影响。掩蔽效应出现在频域（同时掩蔽）和时域（非同时掩蔽）。

同时掩蔽

改编自 Jayant 等人。同时掩蔽的扩展函数。在 1 kHz 处，不同强度的临界频带噪声掩蔽体。

对于同时掩蔽，耳蜗的频率分辨率起着至关重要的作用。在耳蜗内部，发生着频率到位置的转换，并形成了针对不同频带调谐的不同区域。这些不同的频率区域被称为听觉临界频带（或临界带宽）。临界带宽在 500 Hz 以下基本保持恒定，约为 100 Hz，在 500 Hz 以上增加到中心频率的约 20%。 前 24 个临界频带由 Bark 标度描述。音调的存在会导致基底膜的激发，这会影响其临界频带内（带内掩蔽）第二个音调的检测阈值。此外，相邻频带也会受到影响（带间掩蔽）。相邻频带的受影响程度由扩展函数描述。右侧图显示了对不同强度的临界频带噪声掩蔽体进行的测量扩展函数。如图所示，掩蔽体在掩蔽高频带方面比掩蔽低频带更有效，这被称为掩蔽的向上扩展。扩展函数的原因被认为是耳蜗机械滤波特性的副产品，耳蜗中的外毛细胞会放大基底膜的运动，以提高频率分辨率。掩蔽向上扩展的原因尚不明确，除了机械激发之外，抑制也起着作用。此外，由于图中第二个峰值出现在约 2 kHz（1 kHz 的二次谐波）处，因此在更高的声压级下，内耳和中耳的非线性传递特性也起着作用。

强噪声或音调掩蔽体的存在会在基底膜上产生足够强的激发，从而有效地阻断其临界频带内较弱信号的传输，并且掩蔽的扩展也会影响相邻频带。已观察到两种类型的同时掩蔽体：噪声掩蔽音调和音调掩蔽噪声。对于噪声掩蔽音调，音调的存在允许预测被掩蔽噪声频谱的阈值，对于音调掩蔽噪声，噪声的存在允许预测被掩蔽音调的阈值。据报道，纯音和临界频带限制噪声具有不同的阈值。 关于音乐的感知编码，这些阈值会根据感知编码器时频分析的内容进行插值，然后再考虑扩展函数。客观信噪比 (SNR) 可能非常低，例如 20 dB，但取决于音频内容，而主观 SNR 足够高以实现透明编码。 相比之下，音频 CD 的 SNR 为 96 dB。

非同时掩蔽

改编自 Jayant 等人 非同时掩蔽。尖锐的瞬态会在时域中产生影响听觉感知的掩蔽效应。图中所示，瞬态之前（前向或后向掩蔽）和之后（后向或前向掩蔽）的感知都会受到影响。

音频信号中的突然瞬态（或强攻击）会导致时域中的掩蔽效应。图中所示，瞬态之前（前向或后向掩蔽）和之后（后向或前向掩蔽）的感知都会受到影响。后向掩蔽区域持续时间约为毫秒级，而前向掩蔽区域持续时间更长，约为十分之几毫秒。

时间掩蔽尚未完全理解，是一个活跃的研究课题。然而，有证据表明，更高层次的皮质处理参与了这种现象。尚不清楚这种效应是否与声音的整合、神经处理的中断或抑制，以及/或传输速度的差异有关。前向和后向掩蔽表现出不同的特征，因此被认为源于人类听觉系统的不同特性。

掩蔽和联合立体声编码

音频编码中常用的高效技术是联合立体声编码。由于音乐信号的左右声道通常高度相关，因此对音频信号进行求和/差值 (L-R、L+R) 编码有时更有效。在 Mp3 的情况下，求和/差值编码的潜力没有得到充分利用，一种高效的技术是比较左右声道和求和/差值编码的阈值，并动态选择效率更高的编码方式。在计算掩蔽阈值时需要注意，因为联合声道编码会导致由于双耳聆听而产生的可听伪影。

伪影 (w: 压缩伪影)

对于 Mp3 和 AAC，编码比特率是选择的，而不是压缩因子，因为压缩因子取决于内容。较低的比特率会导致更高的压缩比，而较高的比特率会导致较低的压缩比，并且可能出现的伪影的概率也较低。这会导致特定算法表现最佳的工作区域（或比特率），并且在更高的比特率下仅略有改进。 与我们习惯于使用 CD 聆听时所产生的播放设备的噪声和失真伪影不同，感知编码器产生的可听伪影可能令人讨厌。如果比特率太低而无法实现透明编码，则产生的噪声和失真可以描述为时变信号，其中失真与谐波无关，噪声是带限的，并且带宽可能会随帧而变化，信号可能会听起来很粗糙。

带宽损失

如果编码器用完比特，则在频率带宽和低频内容的精确编码之间存在基本权衡。这会导致编码的频率带宽随帧而变化，听起来非常令人不快。通常，这种伪影可以通过限制低比特率的频率带宽来抵消。

前奏

前奏是最难避免的错误，与感知编码器的帧大小有关。如果音频信号的强烈攻击发生在帧的中间，则由于帧大小，计算出的噪声阈值可能会扩展到向后掩蔽区域，从而变得可听。有各种技术可以最大程度地减少前奏的出现，例如可变帧大小分析滤波器组。

与耳蜗过滤特性的关系

总而言之，感知编码利用了人类听觉系统的特性。绝对听阈值与耳蜗的特性有关，但也与中耳和外耳的声学和机械特性有关。在同时掩蔽中，跨临界带宽和内临界带宽掩蔽阈值（扩展函数）源于耳蜗的过滤特性。但是，掩蔽的向上扩展不仅可以用耳蜗的特性来解释，其他现象（如抑制）也可能起作用。最后，时间掩蔽现象只能用听觉系统中较高级别的皮层处理来解释，而联合立体声编码可能产生的伪影也需要双耳聆听来检测，这表明人类听觉系统的各个阶段都参与其中。

人类语音

发声器官

人类的声音是由发声器官产生的。虽然说话似乎毫不费力，但它需要肺部、舌头、上颚、嘴唇和牙齿的复杂运动协调。在皮层水平上，这种运动协调发生在布罗卡区。

人类的发声器官。

术语

响度

声音的强度通常用分贝 (dB) 表示，定义为

$SPL=20*log{\frac {p}{p_{0}}}$

其中 SPL = “声压级”（以 dB 为单位），参考压力为 $p_{0}=2*10^{-5}N/m^{2}$. 请注意，这远小于气压（约 10⁵ N/m²）！还要注意，声音通常以“听力水平”而不是 SPL 为参考。

• 0 - 20 dB SPL ... 听力水平（正弦波音为 0 dB，频率范围 1 kHz – 4 kHz）
• 60 dB SPL ... 中等响度音，日常对话

基频来自声带的振动，成年男性约为 120 Hz，成年女性约为 250 Hz，儿童则可高达 400 Hz。

人类听力损失的频率和响度依赖性。

共振峰

共振峰是人类语音中的主导频率，是由声带信号在口腔等部位的共振产生的。共振峰在声音的频谱中表现为能量的明显峰值。它们从最低频率的共振峰开始按升序编号。

元音的功率谱。声带的振动决定了基频。人类声道中的共振决定了“共振峰”的位置。共振峰的相对位置决定了元音的类型。

德语元音“a,e,i,o,u”的声谱图。这些元音大约对应于英语单词“hut, hat, hit, hot, put”中的元音。使用 MATLAB 命令“spectrogram(data, 512,256, 512, fs)”计算得出。本章节非平稳信号的功率谱描述了声谱图背后的数学原理。

音素

语音通常被认为由一系列被称为音位的声学单元组成，这些声学单元对应于被称为音素的语言单元。音素是用来区分不同单词的最小的语音单位。例如，“dog”这个单词包含三个音素。分别改变第一个、第二个和第三个音素会产生“log”、“dig”和“dot”这些单词。英语据说包含 40 个不同的音素，例如“dog”这个单词中的 /d/、/o/、/g/。

语音感知

人类解码语音信号的能力仍然远远超过目前开发的任何算法。虽然自动语音识别在识别信噪比高的环境中清晰的语音方面取得了相当大的成功，但一旦条件变得不太理想，识别算法的性能往往比人类差得多。由此看来，我们的计算机语音识别算法还没有接近于捕捉人类用于识别语音的底层算法。

有证据表明，语音感知在脑中的路线与其他声音的感知有很大不同。虽然对非语音声音反应的研究通常发现反应与刺激成正比，但语音研究反复发现，当呈现分级刺激时，反应会发生离散化。例如，Lisker 和 Abramson， 播放了预先发声的“b/p”音。声音被解释为 /b/ 还是 /p/ 取决于声门起始时间 (VOT)。他们发现，当平滑地改变 VOT 时，在辅音播放后约 20 毫秒处发生了一个急剧变化，受试者将他们的识别从 /b/ 转换到 /p/。此外，受试者在区分同一类别中的两个声音方面存在很大困难（例如，VOT 为 -10 毫秒到 10 毫秒的声音对，都将被识别为 /b/，而 VOT 为 10 毫秒到 30 毫秒的声音，将被识别为 b 和 p）。这表明正在进行某种分类方案。在试图构建语音感知模型时遇到的主要问题之一是所谓的“不变量缺失”，更直接地说可以被称为“方差”。这个词指的是一个音素（例如，sPeech 或 Piety 中的 /p/）有很多不同的波形与之对应，并且声波形与音素之间的映射远非显而易见，并且高度依赖于上下文，但人类听众却能可靠地给出正确的结果。即使在上下文相似的情况下，波形也会由于语音节奏、说话人身份和说话语气等因素而表现出很大的方差。因此，虽然没有一个公认的语音感知模型，但现有的模型可以分为两类：被动感知和主动感知。

被动感知模型

被动感知理论通常用与大多数感觉信号处理算法相同的方式描述语音感知问题：一些原始输入信号进入，并通过一个层次结构进行处理，其中每个后续步骤从输入中提取一些越来越抽象的信号。早期被动模型的例子之一是特征辨别理论。这个想法是识别某些特征的一组二进制值的出现。例如，“鼻音/口音”、“元音/非元音”。该理论认为，音素被解释为这些特征的存在或不存在的二进制向量。这些特征可以从声谱图数据中提取出来。其他被动模型，例如 Selfridge 和 Uttley 描述的模型，涉及一种模板匹配，其中处理层级的层次结构提取越来越抽象的特征，并且对某些无关特征（例如，在对音素进行分类时，说话人身份）不敏感。

主动感知模型

对语音感知的完全不同的看法是主动感知理论。这些理论指出，大脑拥有两个用于语音感知和语音产生的平行系统是多余的，因为产生声音的能力与识别声音的能力密切相关。这些理论的支持者认为，维持两个独立的数据库（一个包含识别音素的程序，另一个包含产生音素的程序）将是浪费和复杂的。他们认为，语音感知实际上是通过尝试复制传入信号来完成的，因此使用与音素产生相同的电路来进行识别。语音感知的运动理论（Liberman 等人，1967 年）指出，语音声音的识别不是通过任何形式的模板匹配来完成的，而是通过使用语音产生机制来尝试重新生成语音信号的副本。它指出，音素不应被视为语音中的隐藏信号，而应被视为产生机制试图在语音前信号中再现的“线索”。该理论指出，大脑的语音产生区域通过始终听到自己的语音的持续反馈循环来学习哪些语音前信号将产生哪些声音。据认为，婴儿的咿呀学语是一种学习如何从运动前信号中产生这些“线索”声音的方式。

Stevens 和 Halle 在分析合成模型中提出了一个类似的想法。 这描述了一个试图重新生成与传入声音相似的信号的生成模型。它本质上利用了语音产生机制在人与人之间是相似的这一事实，以及说话者可以通过语音中心再现他们在语音中听到的特征。当说话者听到声音时，语音中心会尝试生成传入的信号。比较器会持续反馈关于再生的质量。因此，“感知单位”与其说是传入声音的抽象，不如说是产生相同语音的运动前指令。

当一系列关于现在被称为布罗卡失语症的研究发表时，运动理论遭到了严重打击。这种疾病会损害一个人产生语音声音的能力，而不会损害理解语音声音的能力，而运动理论，以其原始形式，指出产生和理解是由相同的电路完成的，因此受损的语音产生应该意味着受损的语音理解。布罗卡失语症的存在似乎与这一预测相矛盾。

当前模型

语音感知的 TRACE 模型。输入层以外的所有连接都是双向的。每个单元代表语音的某个单位，例如一个单词或一个音素。

语音感知中最具影响力的计算模型之一被称为 TRACE。 TRACE 是一个类似神经网络的模型，具有三层和循环连接方案。第一层从输入频谱图中按时间顺序提取特征，基本上模拟了耳蜗。第二层从特征信息中提取音素，第三层从音素信息中提取单词。该模型包含前馈（自下而上）兴奋性连接、侧向抑制性连接和反馈（自上而下）兴奋性连接。在这个模型中，每个计算单元对应于感知的某个单位（例如音素 /p/ 或单词“荒谬”）。基本思想是，基于其输入，层内的单元将竞争以获得最强的输出。侧向抑制性连接导致一种赢者通吃的回路，其中输入最强的单元将抑制其邻居并成为明显的赢家。反馈连接使我们能够解释上下文相关的理解的影响 - 例如，假设音素层，基于其自下而上的输入，无法决定是否听到了 /g/ 或 /k/，但该音素在 'an' 之前，后面跟着 'ry'。/g/ 和 /k/ 单元最初将被同样激活，并将输入发送到词语级别，该级别已经包含与单词“anaconda”、“angry”和“ankle”相对应的兴奋单元，这些单词已被前面的 'an' 激活。/g/ 或 /k/ 的兴奋